Новый подход к исследованию взаимодействия экономических и социальных факторов

Согласно Концепции долгосрочного социально-экономического развития России на период до 2020 г. обеспечение сбалансированного социально-экономического развития регионов является одной из приоритетных задач государства. Однако современное экономическое пространство России отличается значительными диспропорциями в региональном развитии, и экономическая интеграция регионов и их сбалансированное экономически однородное развитие невозможно при порядковой дифференциации по таким ключевым параметрам, как душевой ВРП, производительность труда, инвестиционная активность. На сегодняшний день большое экономическое неравенство субъектов РФ становится самостоятельным фактором, сдерживающим региональное социально-экономическое развитие.

Несмотря на наличие большого количества работ, посвященных решению проблем неравномерности социально-экономического развития регионов России, в них либо на качественном уровне декларируется результат наблюдений за динамикой социальных или экономических факторов, либо используются только неоклассические модели или модели экзогенного экономического роста, лишь объясняющие взаимосвязь основных экономических показателей (капиталовооруженности, численности населения и темпов роста экономики), но не отражающие зависимость темпов экономического роста от поведения экономических агентов (не учитывающие их неоднородность) и институциональной среды. Таким образом, складывается ситуация, которая «неудовлетворительно описывается классическими теориями региональной экономической динамики» [1]. Между тем, по мнению автора, именно модели эндогенного экономического роста, в которых явным образом учитывается неоднородность экономических агентов, могут наилучшим образом выявить механизм влияния социального неравенства на экономический рост.

В настоящее время основным инструментом измерения уровня неравенства доходов по социальным группам служит так называемый коэффициент Джини, характеризующий степень искривления кривой Лоренца. Хотя коэффициент Джини четко улавливает происходящие сдвиги в распределении доходов между верхними и нижними группами населения, но он не показывает, в какой именно части кривой Лоренца - верхней, средней или нижней - происходят эти сдвиги. Чтобы уточнить характер происходящих сдвигов в практике аналитических расчетов, как правило, используют еще два индикатора: энтропийный коэффициент Тейла и коэффициент Тейла-Бернулли. Однако они плохо приспособлены к оценке аналогичных эффектов применительно к экономике регионов страны, для которых само построение кривой Лоренца весьма проблематично. В этой связи в аналитической практике используются другие показатели неравномерности развития территорий и регионов. Среди них можно назвать коэффициент вариации Клоцвога, в котором учитывается доля населения i -го региона в совокупной численности населения страны и доля ВРП i -го региона в совокупном ВРП страны. Именно коэффициент вариации Клоцвога был использован автором в прикладных расчетах для количественной оценки неравномерности социально-экономического развития федеральных округов и регионов в составе этих округов .

В результате проведенных автором статистических расчетов было установлено, что эффект межрегиональной дифференциации прослеживается как на уровне федеральных округов, так и на уровне регионов в федеральных округах, причем как в наиболее развитом ЦФО, так и в наиболее отсталом ЮФО РФ, что, скорее всего, говорит об универсальности (масштабной инвариантности) этого эффекта (рис.1).

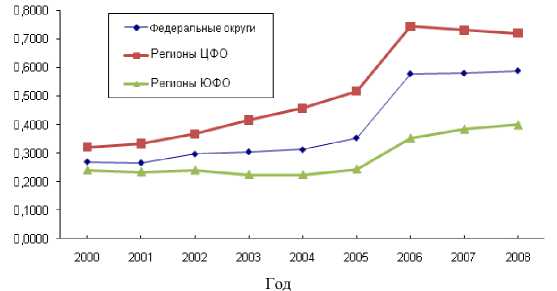
Рис. 1. Динамика коэффициента вариации Клоцвога для федеральных округов РФ, регионов в Центральном и Южном Федеральных округах

Для выявления функции распределения регионов по ВРП автором был проведен статистический анализ регионов по уровню ВРП (рис. 2). Как видно из рисунка 2, распределение регионов по ВРП происходит по двум группам: в первой, многочисленной, группе, где сосредоточено почти 97-99% регионов, находятся регионы с небольшим ВРП (на рис. 2 для 2000 г. ВРП меньше 200 млрд. руб.). Во второй, малочисленной, группе (не более 1-3% регионов) находятся регионы с большим ВРП (на рис. 2 для 2000 г. ВРП больше 200 млрд. руб.). Таким образом, можно проследить фазовое расслоение регионов России по уровню ВРП, которое в многочисленной группе носит характер логнормальной зависимости (на рис. 2 логнормальная зависимость в двойном логарифмическом масштабе представлена в виде параболы), а в малочисленной группе подчиняется степенной зависимости или распределению Парето (в двойном логарифмическом масштабе степенная зависимость имеет вид прямой), и были определены параметры этих функций (рис. 3).

Год

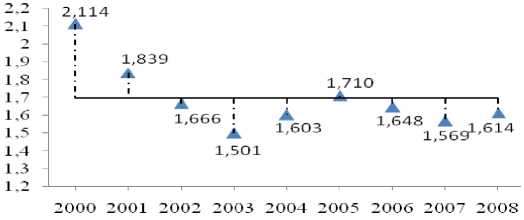
Рис.3. Динамика изменения показателя Парето для степенной части функции распределения регионов по ВРП

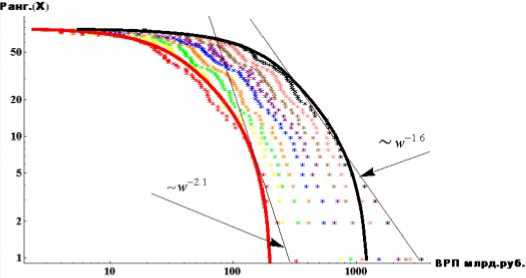
Рис. 2. Динамика изменения функции распределения регионов по ВРП

Из анализа рисунков следует, что для регионов, для которых распределение ВРП носит логнормальный характер, в период с 2000 по 2008 г. не происходит значительных изменений в ВРП, а наибольшей изменчивости подвержены ВРП регионов из малочисленной группы (для них характерно распределение Парето). Как видно из рисунка 3, диапазон изменений показателя Парето колеблется от 1,5 до 2,1.

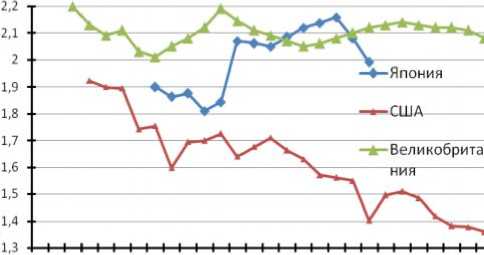
Проведенный автором анализ позволил сделать заключение о том, что распределение регионов России по ВРП носит такой же характер, который касается распределения доходов (богатства) между членами общества в любом обществе в любое время; распределения фирм по производственным показателям (годовая выручка, численность персонала, финансовая капитализация и т.д.); межстранового распределения по ВРП, т.е. это распределение носит универсальный фундаментальный характер, вне зависимости того, что понимается под экономическим агентом и предметом перераспределения. В качестве иллюстрации этого заключения на рисунке 4 приводится динамика показателя Парето для США, Великобритании и Японии (1980-2000 гг.). Как следует из сравнения рисунков 3 и 4, динамика изменения показателей Парето для регионов Российской Федерации происходит в том же диапазоне, что и динамика изменения данного показателя для США, Великобритании и Японии. Это служит подтверждением адекватности авторских расчетов.

1980       1985       1990       1995       2000       2005

Год

Рис.4. Динамика изменения показателя Парето для степенной части функции распределения доходов в США, Великобритании и Японии [3]

Для выяснения природы изменения богатства и механизма его перераспределения в популяции экономических агентов (люди, фирмы, регионы, страны) был разработан авторский подход на основе модифицированной торгово-инвестиционной неравновесной (ТИН) агентной модели Скафетты-Вэста-Пикоцци [4] с учетом параметра, учитывающего различное количество возможных торговых партнеров экономических агентов. В авторской модели рассматриваются два варианта изменения богатства агентов - инвестирование и торговля.

В ТИН-модели богатство i- го агента изменяется с течением времени в соответствии с дискретным нелинейным стохастическим равенством:

N

W(t+1) W(t)+=$(t)W(t)+£ Wj(t),                                (1)

i ^{= 1} ( * i i ) и предполагается, что:

• а)    при совершении торговых операций возможна передача некоторой части богатства от одного агента к другому, так как цена проданного товара колеблется по отношению к равновесной цене, которая равна ее стоимости производства;

• б)    количество богатства, которое может перейти от одного агента к другому при совершении торговых сделок, ограничено количеством богатства более бедного агента;

• в)    цена товара определяется таким образом, чтобы торговые операции статистически были выгодны более бедному агенту.

Выбор ограничения б) продиктован тем, что более богатый агент всегда рискует меньше более бедного. Следовательно, если существует равная вероятность совершения выгодной сделки как для богатого, так и бедного трейдера, то богатство всего общества в конечном итоге будет сконцентрировано в руках богатых агентов, что является классической статистической проблемой, известной под названием «разорение игрока». В реальном обществе такая ситуация, когда все богатство сконцентрировано в руках очень малого количества людей, приводит к экономической нестабильности и заканчивается социальной катастрофой. Следовательно, по мнению автора, для существования социально стабильного общества необходимо сконцентрировать богатство общества в руках наиболее многочисленного среднего класса и выявить принципиальные возможности и механизмы, позволяющие это сделать.

Ключевым предположением автора стал тезис о том, что социальной экономической катастрофы можно избежать, если проводить систематические и постоянные стохастические сдвиги при совершении торговых операций в пользу более бедного агента [ограничение в)]. Эти заведомо созданные благоприятные обстоятельства в пользу бедных должны способствовать передаче им части богатства и воспроизвести безопасное с социальной точки зрения гамма-подобное, или логнормальное, распределение. В ТИН-модели член уравнения, характеризующий инвестиции, представляет из себя мультипликативный стохастический процесс, где r ^ ( t ) - стандартная дисперсия Гауссовой функции распределения ^(t); r i -индекс индивидуальных инвестиций; w , ( t ) - нелинейная стохастическая переменная, описывающая количество богатства, которым обмениваются агенты i and j в процессе торговли, причем w ij = цена -стоимость, если i - это продавец, а j - это покупатель.

В модели также предполагается, что элементы w ij являются случайными Гауссовыми переменными с плотностью вероятности, учитывающей потенциальное среднее значение богатства, которое может быть передано агентами i и j друг другу, и стандартную дисперсию этого распределения. Кроме того, вводится допущение, что в реальной торговле флуктуация богатства, вовлеченного в сделку, должна быть частью (0 < h <  1) богатства более бедного трейдера, а именно:

W ij = W ji = min W , W ] (2)

Так как стандартная дисперсия случайной переменной, т.е. риск, возникающий в процессе торговой сделки, пропорционален h , данная переменная может быть интерпретирована как индекс бедности.

Кроме того, предполагается, что w- = a hW, а переменная а имеет вид нелинейного члена, который яв-ij ij ij                                               ij ляется оценкой внеравновесного характера торговли:

W , - W а„ = f —---

¹j      W , + W j

Параметр f >  0 называется индексом социального равенства и оценивает «благоприятность условий торгового обмена» в пользу более бедного агента.

Для численного изучения динамики изменения богатства изучаемых агентов в модели исследовалось поведение общества, состоящего из 10 5 агентов, которые изначально обладают равным количеством богатства. Компьютерное время наблюдений ограничивалось количеством 10 7 торговых операций. По прошествии этого времени рассчитывалась функция распределения богатства в системе экономических агентов. В результате компьютерных экспериментов с учетом различных значений выбранных управляемых экзогенных параметров: h, f и r в модели были воспроизведены все стилистически наблюдаемые факты (рис. 5-8).

В случае, когда управляемые параметры модели принимают значения: h >  0, f = 0 и r = 0 (моделируется экономика, в которой имеют место только торговые операции с симметричной моделью - с равной вероятностью исхода торговой операции как для бедного, так и для богатого трейдеров), результаты моделирования показывают, что при таких условиях все имеющееся богатство в скором времени концентрируется в руках относительно небольшого количества агентов (из рисунка 5 видно, что с увеличением количества сделок появляется огромная разница в количестве богатства между богатыми и бедными, хотя изначальное распределение в популяции агентов одинаково). Таким образом, полученный результат объясняет механизм и динамику изменения логнормальной части распределения регионов по ВРП с течением времени (см. рис. 2: аналогичным образом себя ведут ВРП регионов в логнормальной части функции распределения регионов по ВРП в 2000 и 2008 гг.).

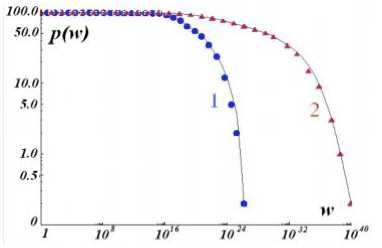
Рис.5. Кумулятивная функция распределения богатства для симметричной модели торговли с индексами h=0.05, f=0, r=0. [(1) - кривая распределения после 1 млн.торговых сделок, (2) - после 10 млн. торговых сделок]. В качестве единицы измерения богатства используется богатство самого бедного агента

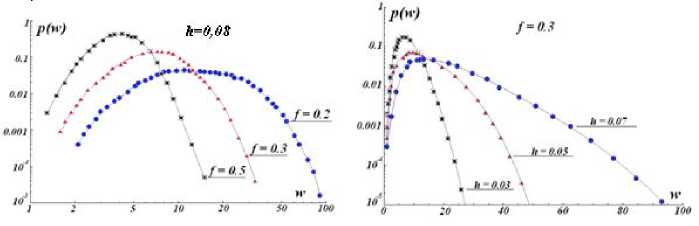
а                                     б

Рис.6. Распределение плотности вероятности богатства для ассиметричной модели торговли: а – с фиксированным индексом бедности h = 0,08

и различными значениями параметра социального равенства f (0,2; 0,3; 0,5);

б – с фиксированным социальным индексом f = 0,3

и разными значениями индекса бедности h (0,03; 0,05; 0,07).

В качестве единицы измерения богатства используется богатство самого бедного агента

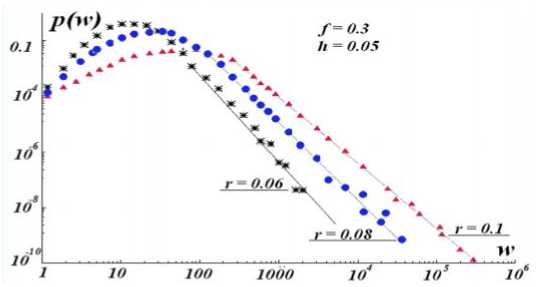
Рис.7. Распределение плотности вероятности богатства в модели с учетом торгово-инвестиционных механизмов. Индексы бедности и социального равенства фиксированы: f = 0,3 и h = 0,05, а индекс инвестиций принимает значения r=0,06; 0,08; 0,1

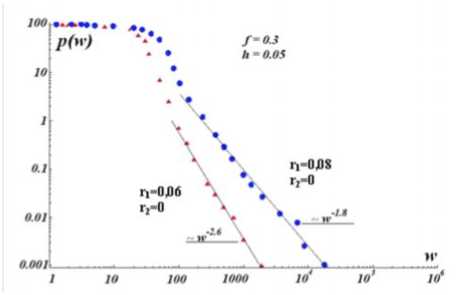
Рис.8. Кумулятивная функция распределения богатства с учетом двойного механизма торговли и инвестиций. Индекс инвестиций для одной части населения – r 2 = 0, для другой – r 1 = 0,08 в первом случае и r 1 = 0,06 во втором случае. Для обоих случаев индекс социального равенства f = 0,3 и индекс бедности h = 0,05. Показатели Парето равны µ = 1,8 ± 0,02 and 2,6 ± 0,02. В качестве единицы измерения богатства используется богатство самого бедного агента

В случае, когда h >  0, f> 0 и r = 0 (асимметричная модель торговли - с включением в модель механизма, который обеспечивает «благоприятность условий торгового обмена» в пользу более бедного агента), результаты эксперимента свидетельствуют о том, что область распределения богатства сужается с увеличением f и смещается в сторону более низких значений, а амплитуда моды увеличивается (рис. 6 а ). Это означает, что вероятность стать богаче снижается с увеличением богатства. И наоборот, для заданного значения f, увеличение индекса бедности h приводит к большему экономическому неравенству и, следовательно, к расширению области распределения богатства (рис. 6 б ).

Таким образом, следует отметить важность полученного результата – модель асимметричной, или внеравновесной, торговли (h > 0 и f > 0, r = 0) принципиально объясняет возможность возникновения значительного по размерам среднего класса в противовес чрезмерно богатой, но малочисленной группе эко- номических агентов и огромному количеству представителей бедного класса, как это наблюдается в симметричной модели торговли, а сам механизм торговли является базой для образования гамма-подобной, или логнормальной, функции распределения, которую мы наблюдаем для бедного и среднего классов в феноменологических данных, характеризующих распределение богатства в популяции экономических агентов (стран, регионов, фирм, населения).

Для моделирования одновременного влияния как механизма торговли, так и механизма инвестиций на динамику изменения богатства в системе экономических агентов были использованы следующие значения параметров: h >  0, f >  0 и r >  0. Как видно из рисунка 7, увеличение r (индекса индивидуальных инвестиций) при прочих равных условиях приводит к дилатации распределения богатства и, следовательно, к увеличению экономического неравенства. В случае если мы сохраняем параметр r постоянным, то результаты численного моделирования показывают, что индекс Парето увеличивается с ростом f и снижается с увеличением h.

Из полученных результатов модельных исследований можно заключить, что модель ТИН, реализующая как механизм инвестиций, так и торговли, может успешно воспроизводить важные феноменологические характеристики реально наблюдаемого распределения богатства в системе экономических агентов: использование только механизма торговли приводит к расслоению общества на большой по численности бедный класс и весьма зажиточный, но небольшой по численности класс богатых (случай симметричной модели торгового обмена) или к расслоению общества на большой по численности средний класс и небольшие по численности бедный и богатый классы (случай асимметричной модели торгового обмена), а использование механизма инвестиции является основным фактором для генерации экспериментально наблюдаемого закона Парето, т.е. хвоста обратной степенной функции для класса богатых.

Таким образом, можно сделать вывод о том, что распределение регионов по ВРП, так же как и распределение богатства в Великобритании и доходов населения Соединенных Штатов, может быть хорошо смоделировано комбинированной функцией распределения, которая описывается логнормальной, или гамма-подобной, функцией для бедного и среднего классов (для класса бедных и средних регионов) и хвостом обратной степенной функции Парето для класса богатых (регионов). Численные исследования автора с использованием методов агентно-ориентированного моделирования также подтверждают этот факт. Результат, полученный автором, дает ответ на вопрос, почему распределение богатства для богатых отличается от других общественных классов – в ходе компьютерных экспериментов было установлено, что различные экономические агенты рассчитывают на разные экономические инструменты: богатые – на инвестиции, иными словами на имеющуюся норму сбережений, остальные ввиду отсутствия нормы сбережений – на торговлю.

На рисунке 8 показаны две кривые суммарных распределений, полученные с помощью следующих параметров: индекс социального равенства f = 0,3, индекс бедности h = 0,05 и инвестиционные индексы для 50% населения r 1 = 0,075 и 0,055, в то время как r = 0 для другой половины в обоих расчетах. На рисунке четко видно, что искусственное двухуровневое разделение общества подчеркивает разницу в распределении богатства между хвостовой областью обратной степенной функции (около 1% населения) и остальной областью (около 99% населения). Из полученного результата можно сделать вывод о том, что дуалистичность экономических механизмов, используемых различными слоями общества, в действительности может быть объяснением того, почему мы наблюдаем двойственное поведение эмпирических кривых. Показатели Парето для двух сглаженных кривых на рисунке 8 равны соответственно a = 1,5 ± 0,02 и 2,5 ± 0,02, что вполне совпадает с эмпирическими значениями для Великобритании, США и Японии (см. рис. 4). Таким образом, увеличение r для склонной к инвестициям части общества приводит к меньшим значениям показателя Парето и, таким образом, к большему экономическому неравенству.

Сегодня можно с уверенностью говорить, что основная проблема неравенства и бедности населения лежит не в плоскости недостатка ресурсов, а в механизмах их распределения и перераспределения, так как существующие механизмы формирования и перераспределения доходов настроены и работают в пользу наиболее обеспеченных слоев населения [2].