Новый подход решения дифференциальных уравнений на основе численного эксперимента

В становлении и совершенствовании методов решения ОДУ заметный вклад внесли такие математики как Эйлер, Гюн, Тейлор, Адамс, Рунге, Кутт, Фехлберг, Милн, Симпсон, Хемминг, Крылов, Чаплыгин и др. [1-4]. С появлением ЭВМ, созданием языков программирования и разработкой удобных прикладных программ численное решение многих математический задач существенно упростилось. В то же время открылась возможность проведения численного анализа решения ОДУ. В данной работе численные методы являлись основным подходом для развития представлений о возможных алгоритмах решения ОДУ. В качестве модельных функций использовались хорошо известные гладкие функции: Sin(x), Cos(x), Exp(x), полиномы P(x). Расчеты проводились на языке программирования Pascal и в программах Mathcad 15, Microsoft Excel, графики рисовались в программе Origin Pro 8-С.

Достижения аналитических подходов.

Задача решения дифференциального уравнения заключается в нахождении (вычислении) функции F(x,y) исходя из набора (таблицы) значений производных y'(x,y) в точках x, x+h, x+h/2, x+2h и др. и начального значения F(x o ,y o ) = Sо. Это частное решение задачи Коши:

y'(x,y)       + F(x o ,y o ) = S o        → F(x,y)

Однако в данной работе мы будем рассматривать более простую задачу, в которой производные и искомая функция зависят только от х:

y'(x)  +  F(x o ) = S о → F(x)

Впервые алгоритм разрешения ОДУ предложил Л. Эйлер. Алгоритм Эйлера позволяет последовательно получать искомый набор F(xi), опираясь на начальное условие F(xo) и набор значений y'(xi).

F(x+h) ~ F(x) + hy'(x)                               (I)

Однако, алгоритм Эйлера на каждом шаге вычисления F(x+h) вносит заметную погрешность, что в итоге приводит к отклонению по сравнению с аналитически полученному решению. Для повышения точности вычисления предложены различные модификации алгоритма Эйлера. Более подробное описание этих методов можно найти в [1-4] и в списке литературы, приведенные в этих книгах. В данной работе мы будем использовать один из самых точных и наиболее распространенный метод Рунге-Кутты четвертого порядка:

F(x i +h,y i ) = F(x i ,y i ) + (k 1 +2k 2 +2k 3 +k 4 )/6,                     (IIа)

ki = hy'(xi,yi), k2 = hy'(xi+h/2,yi+ki/2), кз = hy'(Xi+h/2,yi+k2/2), k4 = hy'(xi+h,yi+k3).

Но поскольку мы в данной работе рассматриваем более простую задачу, в которой исходные значения производных y'(x) и искомая функция F(x) не зависят от yi, то тогда данный метод Рунге-Кутты упрощается:

F( x i +h) = F(x i ) + (k 1 +4k 2 +k 3 )/6,                             (IIб)

k i = hy'(x i ), k 2 = hy'(x i +h/2), k 3 = hy'(x i +h).

Этим упрощенным методом Рунге-Кутты мы будем пользоваться для сравнения с возможностями других подходов.

Численный анализ проблемы решения дифференциальных уравнений.

В уравнении (I) для вычисления последующего значения F(x+h) необходимо предыдущее значение F(x) и y'(x). В книге [2] значения y'(x) в предложено называть функцией приращений ( ФП ). Но так как значения производных не сильно изменяются при малых значениях h, то возможно в уравнении (I) заменять y'(x) на y'(x+h) или y'(x-h). А вот к каким изменениям в решении задачи приведут такие подмены ФП мы попытаемся экспериментально установить. Кроме того в уравнении (I) y'(x) можно заменить на приведенную сумму из двух, или приведенную сумму из большего числа значений производных.

Восстановление первообразных функций Cos(x), x6 и Exp(x)+Exp(-x) исходя из значений y'(xi) в точках x, x+h, x+2h, x+3h и т.д. было решено провести метода Эйлера, в которых ФП были y'(x), y'(x+h), y'(x-h), y'(x+2h).

Результаты представлены на рис. 1.

1а 1б

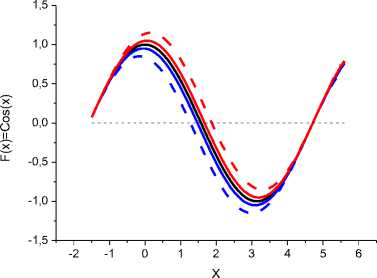
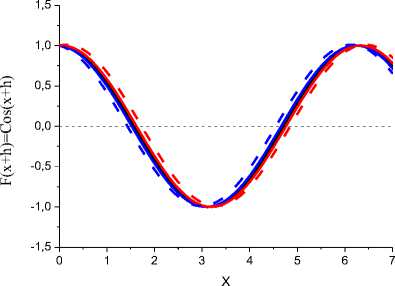
Рис.1а и 1б. Результат решения дифференциального уравнения y'(x) = -Sin(x), F(x+h) = Cos(x+h). Для разных исходных значений F(xo) = Sо (1а -Sо=0; 1б - Sо=1). Точное значение Cos(x+h) - черная линия, красная линия - результаты вычисления F(x+h) = F(x)+hy'(x) (метод Эйлера), синяя линия - F(x+h) = F(x)+hy'(x+h), красная пунктирная линия - F(x+h) = F(x)+ hy'(x-h), синяя пунктирная линия - F(x+h) = F(x)+hy'(x+2h).

1в 1г

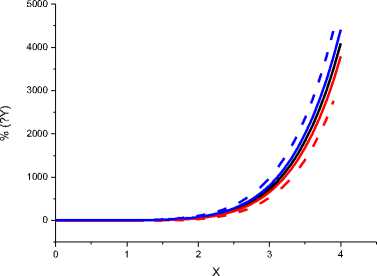
Рис.1в. Результат решения дифференциального уравнения y'(x) = 6x5, F(x) = x6 Точное значение x6 - черная линия. Формулы вычисления и цвета других линий соответствуют подписям к рис 1а.

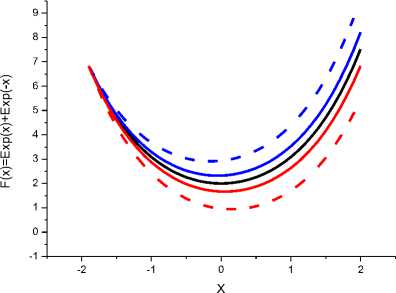
Рис.1г. Результат решения дифференциального уравнения y'(x) = Exp(x)-Exp(-x), F(x+h) = Exp(x+h)+Exp(-(x+h)). Точное значение Exp(x+h)+Exp(-(x+h)) - черная линия. Формулы вычисления и цвета других линий соответствуют подписям к рис 1а.

Из рисунка 1а и 1б следует, что для периодической функции Cos(x) погрешность за один (если x0=n/2+nN) или за пол (если x0=nN) периода обнуляется, что весьма удивительно. Именно это позволяет надежно оценить максимальную погрешность того или иного метода восстановления первообразной. Для непериодических функций с увеличением интервала по х погрешность постоянно накапливается (рис. 1в, 1г), что делает проблематичным оценку погрешности только по конечному значению согласно записи h2*Q(x) [1-4]. Такая оценка погрешности не учитывает факта накопления ошибки. Следует отметить, что периодическое обнуление погрешности для восстановления периодических функций установлена численным методом. А из аналитических рассуждений погрешность должна постоянно накапливаться (увеличиваться), что справедливо для непериодических функций (рис. 1в и 1г). Именно поэтому сначала рассмотрим возможности численного решения дифференциальных уравнений для периодических функций [Cos(x), Sin(x), xpCos(x), Exp(x)Sin(x) и др.]

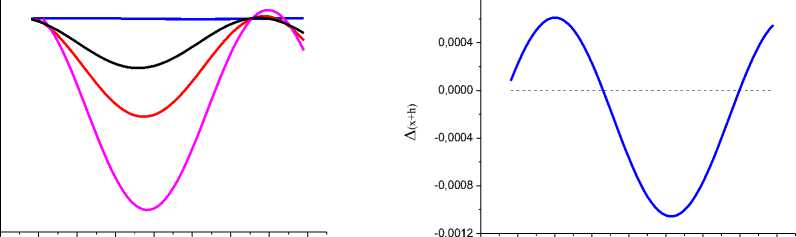
Из рис. 1 следует, что для повышения точности расчетов можно заменить y'(x) на среднее арифметическое [y'(x)+y'(x+h)]/2 (Этот прием в литературе имеет название усовершенствованный метод Эйлера [1, 4]) Возможны также другие ФП, например: [y'(x-h)+y'(x+2h)]/2, [y'(x-2h)+y'(x+3h)]/2, и т.д. (т.н. расширенные методы Эйлера). Но какое среднее арифметическое точнее позволяет вычислять первообразную функцию. На рис. 2 представлены графики разности Cos(x) и результаты решения (A(x+h)=Cos(x+h)-F(x+h)) методом Эйлера и с различными вариантами ФП.

0,0008

0,0

-0,1

-0,2

-0,3

-0,4

-2     -1      0      1      2      3      4      5      6                                 -2     -1      0      1      2      3      4      5      6

XX

2а                             2б

Рис. 2а. Черная линия - Cos(x+h) минус первообразна, вычисленная согласно методу Эйлера: A(x+h)=Cos(x+h)-[F(x)+hy'(x)] , синяя линия -A(x+h) = Cos(x+h)-[F(x)+h[y'(x)+y'(x+h)]/2] (усовершенствованный метод Эйлера), красная линия - A(x+h)=Cos(x+h)-[F(x)+h[y'(x-h)+y'(x+2h)]/2], фиолетовая линия - A(x+h)=Cos(x+h)- [F(x)+h[y'(x-2h)+y'(x+3h)]/2].

Рис. 2б. Более подробно показана синяя линия (усовершенствованный метод Эйлера).

Опираясь на рис. 1 и 2 можно сделать заключение, что алгоритмы решения дифференциальных уравнений обладают симметрией относительно точки x+h/2, что показано на рис.3.

x-2h  x-h    x x+h x+2h x+3h

Рис. 3 Одинаковым цветом выделены точки для составления среднего арифметического из производных (для формирования ФП).

Симметричность, представленную на рис. 3, можно получить только на основе численного эксперимента. Вероятно поэтому, в литературе отсутствует какое-либо упоминание о такой симметрии. Из рис. 3 также следует, что при решении дифференциальных уравнений особым положением обладает точка x+h/2. Поэтому было решено провести численное решение дифференциального уравнения, с ФП в точке x+h/2. В [2] такой алгоритм решения называют методом Эйлера-Коши.

4,00E-008

2,00E-008

0,00E+000

<

-2,00E-008

-4,00E-008

а б

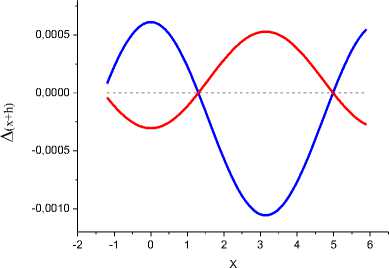
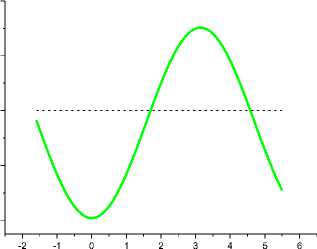
Рис. 4а. Синяя линия - A(x+h) = Cos(x+h) - [F(x)+h[y'(x)+y'(x+h)]/2] (усовершенствованный метод Эйлера), красная линия - A(x+h) = Cos(x+h) -[F(x)+hy'(x+h/2)].

Рис. 4б. A(x+h) = Cos(x+h) - [F(x)+h(4y'(x+h/2)+y'(x)+y'(x+h))/6] -зеленая линия (пояснения в тексте), пунктиром обозначена нулевая линия.

Из рис. 4а следует, что если на «глазок» взять ФП усовершенствованного метода Эйлера [y'(x)+y'(x+h)] и удвоенное значение [y'(x+h/2)], то результат численного решения дифференциального уравнения будет более точным. Среднее арифметическое трех значений h[y'(x)+y'(x+h)]/2 и 2hy'(x+h/2) равно h[y'(x)+4y'(x+h/2)+y'(x+h)]/6. В итоге получим выражение F(x+h) = F(x)+h[4y'(x+h/2)+y'(x)+y'(x+h)]/6, которое совпадает с упрощенным методом Рунге-Кутты (11б). Результат восстановления Cos(x) по формуле (11б) представлен на рис.4б. Из рис. 4 следует, что точность решения усовершенствованным методом Эйлера y'(x)=-Sin(x) не превышает 1*10-3, а исходя из точек в центре симметрии h/2 - 5*10-4, тогда как упрощенный метод Рунге-Кутты - 1*10-8.

Уравнение Рунге-Кутты (Нб) мы получили графически, опираясь на результаты всестороннего численного анализа решения дифференциальных уравнений. Но почему в методе Рунге-Кутты четвертого порядка значение y'(x+h/2) нужно брать в четыре раза больше, чем y'(x) и y'(x+h)? Можно предложить множество различных вариантов, в которых используются значения y'(x), y'(x+h/2) и y'(x+h) и которые приводят к ФП вида: (My'(x+h/2)+Ny'(x)+Ny'(x+h))/(M+2N). Но какой из них самый лучший? Бесспорных аналитических или геометрических доказательств (построений) нет. (См. ПРИЛОЖЕНИЕ 1) Весовые значения вкладов каждой производной можно оценить методом наименьших квадратов, используя функции x4 и x6 и их производные (См. ПРИЛОЖЕНИЕ 2).

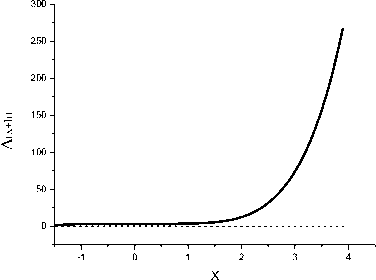
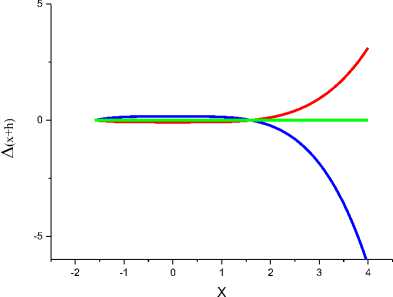
Восстановление первообразных функций, состоящих из произведения периодических функций (Cos(x) и Sin(x)) и показательной или степенной также периодически обнуляется. Рассмотрим теперь восстановление первообразных непериодических функций: xp, Exp(x). Экспериментально было установлено, что метод Эйлера точно восстанавливает только F(x)=x. Усовершенствованный метод Эйлера и метод с ФП равным y'(x+h/2) хорошо восстанавливают F(x)=x2. Метод Рунге-Кутты Пб хорошо восстанавливает первообразную до F(x)=x5. Для функций с большими показателями погрешность возрастает. На рис. 5 представлены результаты восстановления первообразной F(x) = x6 различными методами.

а                                   б

Рис.5а. Ченная линия- A(x+h) = (x+h)6 - [F(x)+ h(y'(x))] (метод Эйлера).

Рис. 5б. Синяя линия - A(x+h) = (x+h)6 - [F(x)+h[y'(x)+y'(x+h)]/2] (усовершенствованный метод Эйлера), красная линия - A(x+h) = (x+h)6 -[F(x)+h[y'(x+h/2)],    зеленая линия - A(x+h) =    (x+h)6    -

[F(x)+h[4y'(x+h/2)+y'(x)+y'(x+h)]/6] - метод Рунге-Кутты (II6).

Как следует из рис. 5 наиболее точно восстанавливает первообразную х6 метод Рунге-Кутты.

Точка h/2 как центр симметрии при решении ОДУ.

Рассмотрим теперь поиск оптимального значения N для решения ОДУ из значения производной в центре симметрии x+h/2 и двух значений в точках x+h/2-hd, x+h/2+hd. Или для ФП: (Ny'(x+h/2)+y'(x+h/2-hd)+y'(x+h/2+hd))/(N+2). Оценку оптимального значения N проводили методом наименьших квадратов согласно выражению: 5 = (x+h)^A6 - (x)^A6 -h[W i y'(x+h/2)+W 2 [y'(x+h/2-hd)+y'(x+h/2+hd)]]/(W i +2W 2 ).         N=W 1 /W 2 .

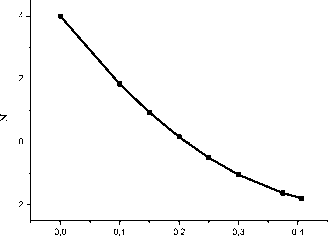
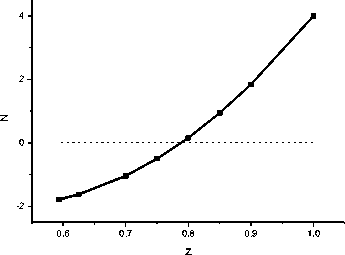
Результаты расчета N представлены на рис. 6.

а б

Рис. 6. Результаты расчетов оптимального значения N в зависимости от z, где z = (h/2-hd)/h, или z=(h/2+hd)/h, hd - расстояния двух производных от центра симметрии. а- для координат точек -hd, б - для координат точек +hd.

Результаты фитирования кривых, представленных на рис. 6а и 6б, приводят к тождественному выражению:

N = 4-24z+24(z)2                        (III)

Опираясь на полученное выражение, потенциально возможно, составлять ФП, включающие производные и за интервалами, приведенными на рис.6. Такие ФП будут в полном согласии с симметрией составления алгоритма решения ОДУ.

Возможные пути улучшения метода Рунге-Кутты

В методе Рунге-Кутты (II6) в интервале [x - x+h] используется три исходных значения y'(x), y'(x+h/2) и y'(x+h). Этот интервал можно разбить на большее число частей. В литературе такие подходы известны, например, в методе Рунге-Кутты-Мерсена используются значения производных в точках x, x+h/3, x+h/2, x+2h/3, x+h [3], а в методе Рунге-Кутты-Фельберга в точках x, x+2h/9, x+h/3, x+3h/4, 5h/6, x+h [3]. Однако, обоснования рабочих формул не совсем ясны. Поэтому мы решили разработать формулы, учитывающие симметричность интервала относительно точки (x+h/2). Для задачи из трех значений у' в точках x+h/3, x+h/2,   x+2h/3   можно предложить несколько формул ФП:

[Ny'(x+h/2)+y'(x+h/3)+y'(x+2h/3)]/(N+2). Установить значение N можно используя выражение (III). Для этого случая значение z=1/3 поэтому по (III) N= -1,3333 = -4/3. Точно такое же значение N получим, если подставить в (III) z=+2/3. Таким образом, ФП будет: [-4/3*y'(x+h/2)+y'(x+h/3)+y'(x+2h/3)]/(-4/3+2), после упрощения получим: [-4*y'(x+h/2)+3[y'(x+h/3)+y'(x+2h/3)]]/2, из чего следует формула:

F(x+h) = F(x)+h[-4y'(x+h/2)+3 [y’(x+h/3))+y’(x+2h/3)]/2]         (IV)

Точно также для значения z=1/4 и z=3/4 получим: N=-0,5=-1/2. После несложных упрощений ФП получим [-y'(x+h/2)+2[y'(x+h/4)+y'(x+3h/4)]]/3:

F(x+h) = F(x)+h[-y'(x+h/2)+2 [y’(x+h/4))+y'(x+3h/4)]/3]          (V)

А для значения z=0 и z=1 получим формулу Рунге-Кутты II6. Для значения z=-1/2 и z=3/2 получим N=22, что приводит к:

F(x+h) = F(x)+h[22y'(x+h/2)+y'(x-h/2))+y'(x+3h/2)]/24          (VI)

Для значения z=-1 и z=2 получим: N=52, что приводит к:

F(x+h) = F(x)+h[52y’(x+h/2)+y'(x-h))+y'(x+2h)]/54            (VII)

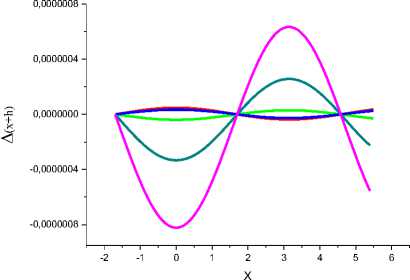
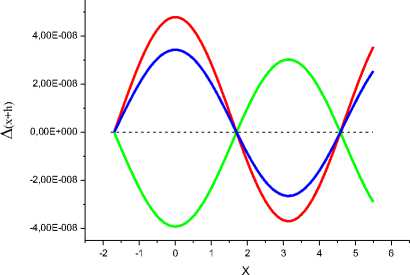
На рис. 7 представлено сравнение результатов восстановления функции Cos(x+h) методом Рунге-Кутты 11б и по формулам IV, V, VI, VII.

а                                  б

Рис. 7а. Зеленая линия - A(x+h) = Cos(x+h) - F(x+h) (расчет методом Рунге-Кутты, по II6). Красная линия - A(x+h) = Cos(x+h) - F(x+h) (расчет по IV), синяя линия - расчет по V, темно-зеленая линия - расчет по VI, фиолетовая линия - расчет по VII.

Рис. 7б. Более подробно показаны зеленая, красная и синяя линии.

Из рис. 7б следует, что результаты, полученные по IV и по V близки по величине к расчету по формуле Рунге-Кутты, но противоположны по знаку. Это потенциально позволяет получить более точные формулы. Особенно интересна формула, в которой ФП II6 сложить с ФП V. В результате получим :                                             (VIII)

Y(x+h) = Y(x)+h[2y'(x+h/2)+4(y'(x+h/4)+y’(x+3h/4))+ y'(x)+y'(x+h)]/12 Эта формула интересна тем, что используются производные, которые располагаются на оси х с равным шагом h/4 внутри интервала [x - x+h].

4,00E-008

2,00E-008

0,00E+000

-2,00E-008

-4,00E-008

X

Рис. 8. Зеленая линия - A(x+h) = Cos(x+h) - F(x+h) (расчет методом Рунге-Кутты, по II6), синяя линия A(x+h) - расчет по V, красная линия -A(x+h) = Cos(x+h) - F(x+h) (расчет по VIII).

Из рис. 8 следует, что при использовании в расчете 5 значений производных (формула VIII) достигается расхождение до 10-9, которое на порядок лучше, чем при использовании в расчетах 3 значения производных (формулы II6 и V). Что вполне согласуется с общим представлением: чем больше точек, тем точнее результат. Потенциально возможно понижение погрешности восстановления первообразной путем более частого разбиения интервала [x - x+h], но такая работа представляет интерес скорее для теоретического исследования. Так как большинство экспериментальных данных обычно получают с точностью не выше 10-3.

Еще одним недостатком метода Рунге-Кутты является то, что в расчетах каждого значения первообразной используются только три значения внутри интервала [x - x+h]. В то время, как экспериментальные значения производных обычно имеются и вне интервала [x - x+h]. Поэтому желательно разработать методику, позволяющую проводить расчеты со значениями производных в более широком интервале. В данной работе предложены формулы для расчета первообразных, используя 5 значений в интервале от [x-h/2 до x+3h/2] (точки x-h/2, x, x+h/2, x+h, x+3h/2) и в интервале от [x-h до x+2h] (точки x-h, x, x+h/2, x+h, x+2h).

Из рис. 7а следует, что если умножить ФП зеленой линии (расчет по II6) в ~8 раз, то она станет близкой к темно-зеленой линии (расчет по VI). Для зеленой и фиолетовой линий оптимальное значение k~23. Это позволяет найти аналитические выражения для оптимального вычисления первообразной Cos(x) исходя из значений в 5 точках:

F(x+h) = F(x)+h[106y’(x+h/2)+32[y,(x)+y’(x+h)]-y'(x-h/2)-y'(x+3h/2)]/168 (IX)

F(x+h) = F(x)+h[768y’(x+h/2)+205[y,(x)+y’(x+h)]-y'(x-h)-y'(x+2h)]/1176 (X)

и 7 точках: (XI)

F(x+h) = F(x)+h[1510y'(x+h/2)+429[y'(x)+y'(x+h)]-7[y'(x-h/2)+ y'(x+3h/2)]-y'(x-h)- y'(x+2h)]/2352

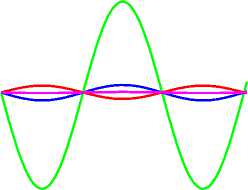
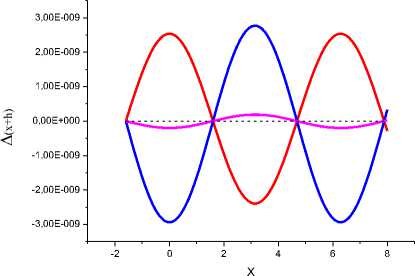
Результаты вычислений по формулам (IX), (X), (XI) представлены на рис 9.

4,00E-008

2,00E-008

-2        0         2         4         6         8

X

а

б

0,00E+000

-2,00E-008

-4,00E-008

Рис. 9а Результаты восстановления функции Cos(x). Зеленая линия -A(x+h) = Cos(x+h) - F(x+h) (метод Рунге-Кутты), красная линия — A(x+h) = Cos(x+h) - F(x+h), восстановление по 5 точкам согласно формуле (IX), синяя линия восстановление по 5 точкам согласно формуле (X), фиолетовая линия восстановление по 7 точкам согласно формуле (XI).

Рис. 9б. Более подробно показана разность между Cos(x+h) и расчетом первообразной по пяти и семи точкам, согласно формулам (IX), (X), (XI).

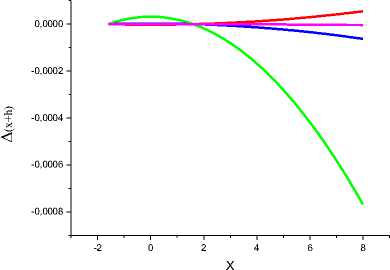
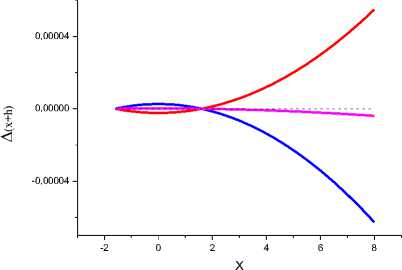
в                                       г

Рис. 9в и 9г. Результаты восстановления первообразной функции x^6. Расчет и цветовое выделение, как и на рис. 9а и 9б.

Формулы (IX), (X), (XI) восстанавливают первообразную Cos(x), x^6 и Exp(x) лучше, чем формула Рунге-Кутты, погрешность которой для восстановления Cos(x) – 4*10-8. Погрешность формул (X) и (X) для восстановления Cos(x) не превышает ~ 2*10-9, а (XI) – 4*10-10. Это вполне согласуется с правилом, согласно которому чем больше значений задействовано, тем точнее результат.

Заключение

В данной работе показано, что решение ОДУ, исходя из массива производных разделенных постоянным шагом h. обладает симметричностью относительно точки h/2. Также показано, что погрешность для периодических функций (например, Cos(x)) при вычислении первообразной через определенные интервалы обнуляется. На основе численного анализа предложена формула (VIII), которая восстанавливает первообразную функцию точнее, чем формула Рунге-Кутты и большинство других известных в литературе формул. Расширение интервала значений производных позволяет повысить точность расчета первообразной, по сравнению с методом Рунге-Кутты до 100 раз. Кроме того формулы (IX), (X), (XI) обладают преимуществом перед формулой Рунге-Кутты так как используется более широкий интервал экспериментальных значений.

В истории математики аналитические и геометрические построения всегда являлись основой для вывода формул и формирования общих представлений о решении различных задач. Численный эксперимент обычно являлся рабочей лошадкой, с помощью которой подтверждались выводы, полученные аналитическими или геометрическими подходами. Сто лет назад проводить численное моделирование было весьма трудной задачей. Спустя 30-40 лет стали появляться первые компьютеры. К началу XXI века возможности ЭВМ многократно возросли. Также были разработаны и получили широкое распространение такие языки программирования, как Fortran, Packal, Cu, Delphi и др. Кроме того были созданы удобные программы Microsoft Excel, Origin, Mathcad и др. Благодаря всему этому стало возможным проводить всестороннее численное моделирование многих математических задач и сопоставлять результаты решения, полученные разными методами. В данной работе проведен численный анализ проблемы восстановления первообразной, который развивает общие представления о решении дифференциальных уравнений. В данной области математики численный метод является определяющим при выборе наиболее точного выражения из некоторого числа вариантов, которые могут быть предложены аналитическими или геометрическими подходами. Таким образом, численный эксперимент в задаче восстановления первообразной становится необходимым элементом, без которого невозможно установить оптимальную формулу решения ОДУ.

Цель данной работы разрушить представления о том, что только аналитическими или геометрическими методами возможно построить оптимальные представления о решении ОДУ. В фундаменте основ решения ОДУ должны быть положены также данные численного эксперимента и симметричности составления ФП.