Новый способ сокращения времени моделирования итеративного декодирования

Среди прочих теорем, сформулированных Клодом Шенноном в его фундаментальной работе [1], теорема о канале с шумами не только установила теоретическую границу возможности передачи с заданной скоростью, но и, связав возможность передачи без ошибок с длиной кодового блока, породила новое направление в теории кодирования — изучение возможности создания и использования кодовых конструкций с большой длиной блока. Наиболее известными на сегодняшний день являются турбо-коды и коды с малой плотностью проверок на чётность (МППЧ-коды). Ранее было показано [2], что для МППЧ-кодов можно предложить эффективный способ их использования в сетевом кодировании. Однако данный способ, использующий итеративное декодирование и генерирование проверочных матриц кода «на лету», значительно усложняет аналитическое исследование характеристик предложенных методов. В связи с этим основным инструментом для изучения характеристик кодов и их зависимости в том числе от структуры сети является численное моделирование.

В процессе моделирования используется значительное количество вычислительных мощностей, большая часть которых расходуется на процедуру поиска и исправления ошибок в некотором принятом векторе. Для этого используется алгоритм итеративного декодирования, как он описан в [3]. С использованием данного алгоритма декодирование кодового блока разбивается на отдельные итерации , каждая из которых включает в себя горизонтальный и вертикальный шаги. Количество итераций может быть жёстко задано (25, 50, 100), а также регулироваться дополнительными условиями. Например, декодирование может прерваться, если полученный по окончании очередной итерации кодовый вектор не содержит ошибок.

Во время работы алгоритм использует несколько матриц, представляемых в памяти компьютера двухмерными массивами:

• •    массивы вероятностей q0 и q1;

• •    массивы поправок r0 и r1.

Данные массивы имеют размеры, равные размерам проверочной матрицы. В целях увеличения скорости исполнения используются также двухмерные массивы с переменным числом элементов в строках: массив проверок в строках и массивы проверок в столбцах (соответствуют множествам N(m) и M(n), описанных в [3]). Они строятся один раз на основании проверочной матрицы кода. Кроме этого используются некоторые промежуточные массивы.

Если опустить операции присваивания и ветвления, основные циклы алгоритма с учётов вложенности выглядят следующим образом:

• 1.    Цикл итераций.

  • 1.1.    Горизонтальный шаг.

    • 1.1.1.    Цикл по строкам.

      • 1.1.1.1.    Цикл по индексам N(m).

      • 1.1.1.2.    Цикл по индексам N(m).

        • 1.1.1.2.1.    Цикл по индексам N(m).

        • 1.1.1.2.2.    Цикл по индексам N(m).

      • 1.1.1.3.    Цикл по индексам N(m).

      • 1.1.1.3.    Цикл по индексам N(m).

  • 1.2.    Вертикальный шаг.

    • 1.2.1.    Цикл по столбцам.

      • 1.2.1.1.    Цикл по индексам M(n).

        • 1.2.1.1.1.    Цикл по индексам M(n).

      • 1.2.1.2.    Цикл по индексам M(n).

      • 1.2.1.3    Цикл по строкам.

      • 1.2.1.4.    Цикл по индексам M(n).

Как видно из приведённого списка, самые «глубокие» циклы являются циклами с относительно малым количеством итераций, так как количество элементов во множествах N(m) и M(n) соответствует количеству «1» в строках и в колонках соответственно (а для МППЧ-кодов оно мало по определению).

Циклы с малым числом итераций могут отрицательно сказываться на производительности из-за особенностей работы предсказателей ветвления процессора. Поэтому если бы можно было «раскрыть» подобные циклы, преобразовав их в набор инструкций для каждой строки и для каждого столбца, это могло бы дать выигрыш в производительности.

Дополнительно нужно учесть, что язык Java не содержит определения массива как константы. Ключевое слово final может объявить ссылку на массив константой, но не запретит изменять программе содержимое массива. Таким образом, JIT-компилятор не имеет права в общем случае предполагать, что final-массив является константой сам по себе, и его значения можно включить в программу, не вычисляя их каждый раз.

Система моделирования написана на Java и в вопросах производительности опирается на возможности среды исполнения и на средства языка Java по указанию компилятору способов оптимизации. Однако язык Java, в отличие от С / С + + , не содержит инструкций для JIT-компилятора, то есть программист не может прямым способом указывать JIT-компилятору, какие циклы должны быть раскрыты. Аналогично, нет и способа указать, что массив или структура данных является константой.

Поэтому предлагается использовать информацию из проверочной матрицы, в частности, множества M(n) и N(m) для генерации байт-кода программы на языке Java в тот момент, когда программе станет известна проверочная матрица кода. Для этого будем использовать библиотеку Javassist [4]. Рассмотрим этот процесс подробно на примере горизонтального шага. Оригинальный код приведён ниже:

• 1.    for (int row = 0 ; row <  rows; row++) {

• 2.    final float q0Row = q0[row];

• 3.    final float q1Row = q1[row];

• 4.    final float r0Row = r0[row];

• 5.    final float r1Row = r1[row];

• 6.    final int usedIndexes = checksOfRow[row];

• 7.    final int usedIndexesLength = usedIndexes. length;

• 8.    final float deltaQRow = newfloat[usedIndexesLength];

• 9.    for (int i = 0 ; i <  usedIndexesLength; i++) {

• 10.    final int column = usedIndexes[i];

• 11.    deltaQRow[i] = q0Row[column] — q1Row[column];

• 12.    }

• 13.    final float deltaValues = newfloat[usedIndexesLength];

• 14.    Arrays. fill (deltaValues, 1f);

• 15.    for (int i = 0 ; i <  usedIndexesLength; i++) {

• 16.    for (int k = 0 ; k <  usedIndexesLength; k++) {

• 17.    if (i! = k) {

• 18.    deltaValues[i] * = deltaQRow[k];

• 19.    }

• 20.    }

• 21.    }

• 22.    final float deltaValues_p = new float[usedIndexesLength];

• 23.    finalfloat deltaValues_m = new float[usedIndexesLength];

• 24.    for (int i = 0 ; i <  usedIndexesLength; i++) {

• 25.    deltaValues_p[i] = (1 + deltaValues[i]) / 2 ;

• 26.    deltaValues_m[i] = (1 — deltaValues[i]) / 2 ;

• 27.    }

• 28.    int counter = 0 ;

• 29.    for (int column: usedIndexes) {

• 30.    r0Row[column] = deltaValues_p[counter];

• 31.    r1Row[column] = deltaValues_m[counter++];

• 32.    }

• 33.    }

Наличие информации о проверочной матрице кода позволяет сделать изменения в данном отрезке программы, уменьшающие время его работы. Во-первых, код основного цикла 1--32 можно заменить на код вызова подпроцедур performHorizontalStep$1(), performHorizontalStep$2() и т. д., где номер в имени процедуры означает номер соответствующей строки, тем самым раскрывая цикл и делая переменную row константой для каждой из подпроцедур.

Во-вторых, после переноса каждого шага цикла в подпрограмму указатель на массив usedIndexes также становится константой в рамках каждой из подпроцедур, как и значения данного массива. Поэтому в каждой из подпрограмм мы можем заменить циклы 9--12, 16--20, 15--21, 24 -- 27 на набор инструкций с прямым указанием значений индексов (известных из проверочной матрицы).

В-третьих, так как размер вспомогательных массивов нам известен, то мы можем заменить один массив на множество переменных, что также может дать выигрыш, так как компилятору не придётся вставлять дополнительный код для проверок границ массива при каждом обращении, а сами переменные он может частично разместить в регистрах процессора и не выделять под них память в «куче».

В результате для первой строки кода ««96.3.963 (N = 96 , K = 48 , M = 48 , R = 0 .5)» из [5] будет сгенерирована следующая подпроцедура performHorizontalStep$0():

• 1.    {

• 2.    final float q0Row = q0[0]; final float q1Row = q1[0];

• 3.    final float deltaQRow_7 = q0Row[7] — q1Row[7];

• 4.    final float deltaQRow_19 = q0Row[19] — q1Row[19];

• 5.    final float deltaQRow_35 = q0Row[35] — q1Row[35];

• 6.    final float deltaQRow_55 = q0Row[55] — q1Row[55];

• 7.    final float deltaQRow_79 = q0Row[79] — q1Row[79];

• 8.    final float deltaQRow_80 = q0Row[80] — q1Row[80];

• 9.    final float delta_7 = deltaQRow_19 * deltaQRow_35 * deltaQRow_55 * deltaQRow_79 * deltaQRow_80;

• 10.    final float delta_7_p = (1 + delta_7) / 2 ; final float delta_7_m = (1 — delta_7) / 2 ;

• 11.    final float delta_19 = deltaQRow_7 * deltaQRow_35 * deltaQRow_55 * deltaQRow_79 * deltaQRow_80;

• 12.    final float delta_19_p = (1 + delta_19) / 2 ; final float delta_19_m = (1 — delta_19) / 2 ;

• 13.    final float delta_ 35 = deltaQRow_7 * deltaQRow_19 * deltaQRow_55 * deltaQRow_79 * deltaQRow_80;

• 14.    final float delta_35_p = (1 + delta_35) / 2 ; final float delta_35_m = (1 — delta_35) / 2 ;

• 15.    final float delta_ 55 = deltaQRow_7 * deltaQRow_19 * deltaQRow_35 * deltaQRow_79 * deltaQRow_80;

• 16.    final float delta_55_p = (1 + delta_55) / 2 ; final float delta_55_m = (1 — delta_55) / 2 ;

• 17.    final float delta_ 79 = deltaQRow_7 * deltaQRow_19 * deltaQRow_35 * deltaQRow_55 * deltaQRow_80;

• 18.    final float delta_79_p = (1 + delta_79) / 2 ; final float delta_79_m = (1 — delta_79) / 2 ;

• 19.    final float delta_ 80 = deltaQRow_7 * deltaQRow_19 * deltaQRow_35 * deltaQRow_55 * deltaQRow_79;

• 20.    final float delta_80_p = (1 + delta_80) / 2 ; final float delta_80_m = (1 — delta_80) / 2 ;

• 21.    final float rORow = r0[0]; final float r1Row = r1[0];

• 22.    r0Row[7] = delta_7_p; r1Row[7] = delta_7_m;

• 23.    r0Row[19] = delta_19_p; r1Row[19] = delta_19_m;

• 24.    r0Row[35] = delta_35_p; r1Row[35] = delta_35_m;

• 25.    r0Row[55] = delta_55_p; r1Row[55] = delta_55_m;

• 26.    r0Row[79] = delta_79_p; r1Row[79] = delta_79_m;

• 27.    r0Row[80] = delta_80_p; r1Row[80] = delta_80_m;

• 28.    }

Хотя сама процедура выглядит длиннее, она более не содержит ни одного цикла и, что важнее, ни одной явной проверки условий, кроме неявных проверок на границы массивов в строках 2--8 и 21--27. При этом сама процедура горизонтального шага будет выглядеть как

• 1.    { 2. performHorizontalStep$0(); ....... 49. performHorizontalStep$47(); }

Аналогичным образом меняется и процедура вертикального шага.

В качестве средства генерации байт-кода использовалась библиотека Javassist, так как она позволяла генерировать код из строк псевдокода, напоминающего Java-код, приведённый выше. Работа с библиотекой сводится к следующему.

• 1.    Получить от управляющей программы матрицу проверочного кода.

• 2.    Скопировать в память под новым именем готовый класс стандартного декодера.

• 3.    На основании матрицы сгенерировать подпроцедуры для горизонтальных и вертикальных шагов для каждой строки и столбца — с помощью простой конкатенации строк.

• 4.    Заменить методы вертикального и горизонтального шагов в скопированном классе на новые, осуществляющие последовательный вызов подпроцедур. Аналогично, с помощью конструирования и конкатенации строк.

• 5.    Выполнить метод toClass () и создать новый экземпляр объекта декодера.

• 21.

• 22.    r0. r_0_7 = delta_7_p; r1. r_0_ 7 = delta_7_m;

• 23.    r0. r_0_ 19 = delta_19_p; r1. r_0_ 19 = delta_19_m;

• 24.    r0. r_0_ 35 = delta_35_p; r1. r_0_ 35 = delta_35_m;

• 25.    r0. r_0_ 55 = delta_55_p; r1. r_0_ 55 = delta_55_m;

• 26.    r0. r_0_ 79 = delta_79_p; r1. r_0_79 = delta_79_m;

• 27.    r0. r_0_ 80 = delta_80_p; r1. r_0_ 80 = delta_80_m;

Кроме описанных изменений можно произвести дополнительное изменение механизма доступа программы к значениям массивов r0 и r1, а точнее, заменить их на два экземпляра отдельного генерируемого класса с большим числом переменных. Однако, так как нам нужны лишь те значения массивов r0 и r1, которые соответствуют «1» в проверочной матрице кода, количество этих переменных также будет ограничено. Тогда в том числе строки 21--27 будут выглядеть следующим образом:

Подобное изменение уменьшает количество проверок на превышение границ массива, а также требует меньше памяти, чем предыдущий вариант.

Результаты моделирования. На рис. 1 показано время моделирования без предварительной генерации кода декодера с генерацией, а также с генерацией и с заменой массивов r0 и r1 на переменные дополнительного класса. Моделирование выполнялось с использованием проверочной матрицы МППЧ-кода «408.3.834 (N = 408, K = 204, M = 204, R = 0.5)» из [5].

Как видно из рис. 1, предложенный метод уменьшения времени моделирования даёт существенный выигрыш во времени. Дополнительно на рис. 2 приведены результаты в процентах к времени без изменения кода алгоритма.

Предложенный в статье способ частичной генерации байт-кода на основе информации из проверочной матрицы блочного кода позволяет уменьшить время моделирования алгоритма работы итеративного декодера кодов с малой плотностью проверок на чётность. Аналогичный способ может быть предложен для других алгоритмов, основанных на использовании больших разреженных матриц, например для недвоичных кодов с малым количеством проверок.

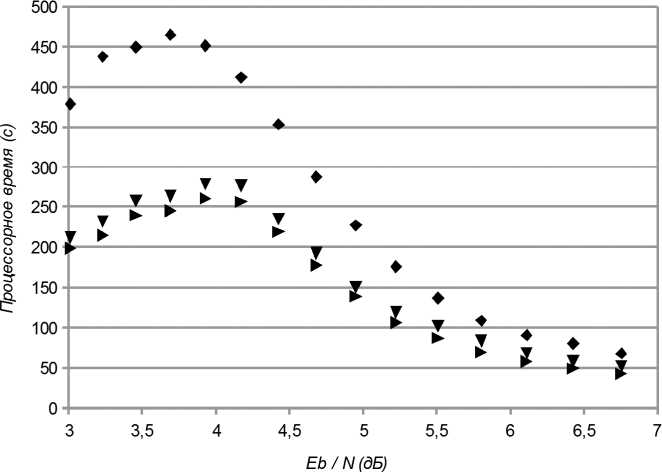
♦ Без предгене- ▼ С генерацией ► С генерацией рации байт-кода байт-кода байт-кода и заменой массивов

Рис. 1. Время моделирования без использования и с использованием предварительной генерации байт-кода декодера

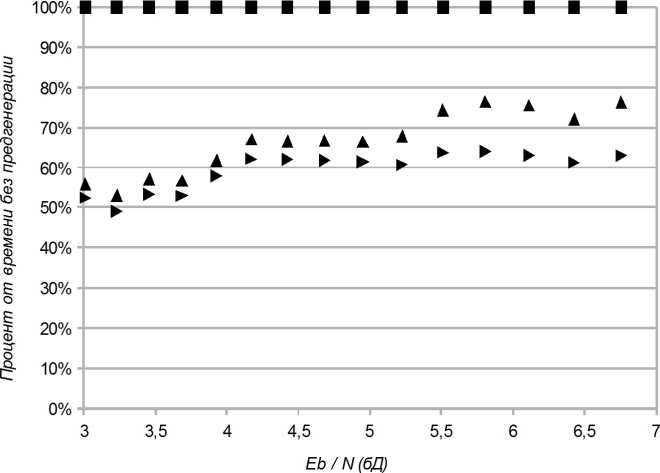
■ Без предгене- * С генерацией ► С генерацией рации байт-кода байт-кода байт-кода и заменой массивов

Рис. 2. Время моделирования с использованием предварительной генерации байт-кода декодера в процентах от времени без использования генерации