Новый взгляд на модифицированный принцип Ферма: нелинейная оптика через призму термодинамики световых траекторий
Автор: Шиллер М.П., Камалетдинова А.И., Иванова О.С., Салеев И.С., Трандин С.Е.
Журнал: Теория и практика современной науки @modern-j
Рубрика: Физика и астрономия
Статья в выпуске: 5 (119), 2025 года.
Бесплатный доступ
В статье представлен новый подход к описанию световых траекторий в нелинейных оптических средах на основе модифицированного принципа Ферма с использованием концепций термодинамики. Традиционный принцип Ферма, формулирующий путь света как экстремум оптического времени, расширяется с учетом нелинейных взаимодействий и диссипативных процессов. Предложена формализация световых траекторий через минимизацию функционала, учитывающего не только оптическую длину пути, но и энтропийные и энергетические характеристики среды. Приведены основные уравнения, раскрывающие связь между нелинейной оптикой и термодинамическими законами, а также обсуждены перспективы применения данного подхода в управлении светом и разработке новых оптических устройств.
Принцип ферма, нелинейная оптика, термодинамика, световые траектории, оптическое время, диссипация, минимизация функционала
Короткий адрес: https://sciup.org/140311697
IDR: 140311697
A new look at the modified Fermat’s principle: nonlinear optics through the prism of thermodynamics of light trajectories
The paper presents a new approach to the description of light paths in nonlinear optical media based on a modified Fermat's principle using concepts of thermodynamics. The traditional Fermat's principle, formulating the light path as an extremum of optical time, is extended to take into account nonlinear interactions and dissipative processes. The formalization of light paths through the minimization of a functional that takes into account not only the optical path length, but also the entropic and energy characteristics of the medium is proposed. The basic equations revealing the connection between nonlinear optics and thermodynamic laws are given, and the prospects of application of this approach in light control and development of new optical devices are discussed.
Текст научной статьи Новый взгляд на модифицированный принцип Ферма: нелинейная оптика через призму термодинамики световых траекторий
Принцип Ферма является фундаментальным законом геометрической оптики, который утверждает, что свет распространяется по пути, минимизирующему оптическое время. В классической формулировке он успешно описывает поведение света в линейных и однородных средах. Однако современные оптические технологии все чаще требуют учета нелинейных эффектов, диссипации и взаимодействия света с активными и сложными средами. В связи с этим возникает необходимость модификации принципа Ферма и расширения его формализма.
В данной работе рассматривается новый взгляд на принцип Ферма, основанный на термодинамическом подходе к световым траекториям в нелинейных оптических системах. Предлагается рассматривать световой путь как результат минимизации функционала, включающего оптическое время и термодинамические параметры, такие как энтропия и энергия диссипации.
Традиционный принцип Ферма
Классический принцип Ферма формулируется следующим образом:
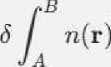
где n(r) — показатель преломления среды в точке r, ds — элемент длины траектории света от точки A до точки B, а оператор δ означает вариацию интеграла. Этот принцип утверждает, что свет выбирает путь, при котором оптическая длина пути (или оптическое время) является экстремумом (обычно минимумом).
Модификация принципа Ферма для нелинейной оптики
В нелинейных средах показатель преломления зависит от интенсивности света I(г), что приводит к усложнению траекторий и появлению эффектов самофокусировки, модуляции фазы и др. В этом случае:
п = п0 + n2I(r), где n0 — линейная часть показателя преломления, n2 — коэффициент нелинейности.
Традиционный принцип Ферма не учитывает энергообмен с окружающей средой и диссипацию. Для описания этих процессов вводится термодинамический функционал F:
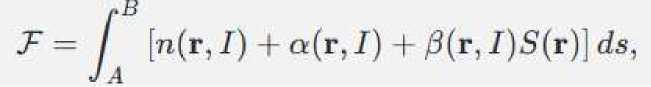
где:
-
• a(r, Г) — функция, описывающая потери энергии (диссипацию),
-
• Р (r, I)S(r) — вклад энтропии S(r) S ( r ) в функционал,
-
• Р (r, Г) — коэффициент, связывающий локальную энтропию с оптическим процессом.
Минимизация F по траектории света дает уравнения движения, учитывающие нелинейные и термодинамические эффекты.
Связь с уравнениями нелинейной оптики
Рассмотрим уравнение нелинейной оптики в параксимальном приближении:
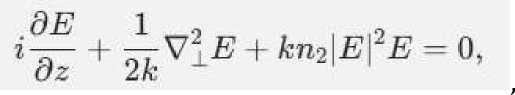
где E — амплитуда электрического поля, к = 2пп0/Лк — волновое число, V 1 2 — лапласиан по поперечным координатам.
Введение термодинамических параметров позволяет дополнить эту модель уравнениями для энергетического баланса и энтропии, что приводит к системе уравнений, описывающих динамику световых пучков с учетом диссипации и термодинамических потерь.
Обсуждение
Предложенный модифицированный принцип Ферма позволяет рассматривать световые траектории как оптимальные пути в расширенном пространстве параметров, включающем не только геометрические, но и термодинамические характеристики. Такой подход открывает новые возможности для управления светом в нелинейных и активных средах, включая разработку оптических устройств с заданными свойствами диссипации и управления энтропией.
Заключение
В статье представлен новый взгляд на принцип Ферма, расширенный с учетом термодинамики световых траекторий в нелинейных оптических средах. Предложенная теория объединяет классическую геометрическую оптику с концепциями термодинамики, что позволяет более полно описывать сложные процессы распространения света в реальных материалах. Данный подход может стать основой для разработки новых методов управления светом и создания инновационных оптических систем.
