Number of physical connectivity states in transfer matrix method for enumeration of Hamiltonian circuits in rectangular lattice

The enumeration of all possible Hamiltonian circuits in grid graphs is one of the most important and fundamental problems of combinatorics. It has many applications in mathematics, physics, biology, etc. One of the most famous applications is connected with the polymer science. Hamiltonian circuits correspond to conformations of macromolecules [2]. There are different ways to solve this enumeration problem, but the best way is to use the so-called transfer matrix method [1], [4]. Unfortunately, application of this method requires a huge amount of RAM on your PC because the order of a transfer matrix grows apparently with the increase of the parameter m of the grid P x P n . The number of all possible connectivity states is given by Motzkin numbers:

Mot(m)                   ~        3m , while m k0 k1k2k4m3                     .

One can see that increasing m by 1 extends the number of connectivity states approximately three times. Kloczkowski and Jernigan [4] have recently suggested a rule that helps to divide the set of all connectivity states into the so-called physical and unphysical states. Our goal is to obtain a formula for the exact number of physical states. We strongly convinced that such a formula will help to understand the real bounds on m and n for which can be calculated the number of Hamiltonian circuits in P_m x P n lattice. Let us recall that the biggest lattice with the Iknown value of circles is P 22 x P [1], [3]. We assume that the reader is familiar with the transfer matrix method for enumeration of the number of Hamiltonian circuits in P x P n [1], [4]. We use the definitions given in [4] and after some necessary explanations immediately start with the construction of the formulae.

FORMULAE CONSTRUCTION

We can imagine the construction of any Hamiltonian circuit as an iterative procedure of append

ing the vertical and horizontal bones level by level from the bottom to the top of a lattice. Let’s fix the “cut line” as it is shown in fig. 1. The part of the circuit lying below the cut line consists of two disjoint chains. Another part of the circuit (gray solid line in fig. 1) lying over the cut line is just a variant of extending the chains. The connectivity state is a level P m of P m x P n lattice with those sites connected by arc, which belong to the end points of the same chains.

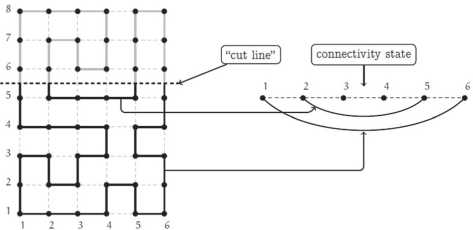
Fig. 1. The connectivity state in P 6 x P 8 lattice

If we imagine all possible ways of connecting sites in a level P_m , we will get Mot( m ) number of all connectivity states [4]. But not all of the states are physical and correspond to some cut of realy existing Hamiltonian circuit. Let us describe the rule for identifying physical and unphysical states with some inconspicuous variations from [4].

First, let us consider that m is even and fix some connectivity states with m sites. Let us assign parities “+1” and “-1” one by one to all the sites. Then let us sum the parities of all the unconnected sites. If the sum is equal to zero then the connectivity state is physical, otherwise it is unphysical. If m is odd then we act the same way, but the sum of parities of all the unconnected sites should be equal to “+1” or “-1”. For example, the connectivity states in fig. 2(a, c, e, f) are physical, but the connectivity states in fig. 2(b, d) are unphysical.

The number of physical connectivity states in the transfer matrix method for enumeration of hamiltonian circuits...    113

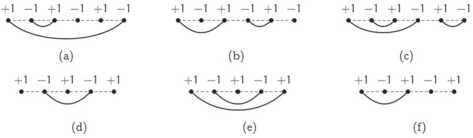
Fig. 2. Physical and unphysical states: (a), (c), (e) and (f) are physical, (b) and (d) are unphysical

sites. The Catalan number gives the number of ways to connect the chosen sites:

Mj i /2kj/pmi2 jjp-m(2 jj _ 27^3 ^ 3m k=0 k +1 ^ k J^ k Д k J 2nm2 '

Let us count the number of physical states corresponding to the described rule. Begin with even m . Consider 2 k of m sites connected. Due to the rule k

The same way to it, if we need to make the sum of all parities of unconnected states equal minus one, we have to choose k + 1 site from m 2 “positive” sites and k – 1 sites from m 2 “negative” sites:

sites have the parity “+1” and k sites have the parity “-1”. One can choose 2 k sites with this property from

V-m ^ ^j 1 / ² k Jp" mJ 2 jj IL m] 2 Jj _ 27^3 ^ 3 m _k = ₀ k + 1 ^ k J^ k + 1 J^ k - 1 J 2 nm²

The number of all physical states for odd m is equal to B ( m ) + C ( m ).

ways. On having done this a connec-

m 2

k ₁ tion of the chosen sites in

m by

2 k

k 1 k

ways (Catalan

numbers) can be made. As a result, we get the number of physical states summing for all possible k :

m /2                           ²

1 I 2k II ml2 I A( m) = > k=0k +1 ( k J( k J

9J3

-9^ • 3 ^m , while m ^^ . 2 nm

As we can see the number of physical states is asymptotically m times smaller than the number of all the connectivity states Mot( m ).

Now let us suppose m is odd. If the sites are numbered from “+1” then we have more “positive” sites rather than “negative” ones by one. Let us consider again 2 k of m sites are connected. First we should make the sum of parities of unconnected states equal plus one. Then we have to choose k site from m 2 “positive” sites and k sites from m 2 “negative”

DISCUSSION

The determined formulae give us the exact number of physical states. As we can see, the number of such states is asymptotically m smaller than the known upper bound Mot( m ). Instead of being reduced, the number of physical states grows very fast. Of course, it is possible to halve the number of physical states using the central reflection of P_m but it will hardly help to considerably reduce the size of the transfer matrix. Our formulae help to understand how many resources you will need to calculate the exact number of Hamiltonian circuits in a given lattice P m x P n . For example, the nearest unsolved problem is the number of Hamiltonian circuits in P 24 x P 24 . Our formula gives A (24) = 1 079 364 105 physical states. This is 3 times less than Mot(24) = 3 192 727 797. Number A (24) can be halved (if we don’t take a small number of symmetrical states into account), but nevertheless it is not enough to start counting on home PC.

* Работа выполнена при поддержке Программы стратегического развития (ПСР) ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.