Numerical investigation of influence thermal preparation coal on nitric oxides formation in combustion process

Existing problems of using coal in the boiler units to a large extent can be overcome by the burning of coal dust to expose to heat treatment directly at the plant. Heat treatment of coal samples leads to significant changes in the composition and properties of solid residue, which is to reduce the yield of volatile substances and oxygen, to increase the caloric content of residual volatile matter and calorific solid residues. Good flammability of products of heat treatment, high caloric content and their reactivity, environmental cleanliness provide ample opportunities for use in thermal power plants the pre-thermal preparation of coal before burning.

In 1980-1983 at the experimental facility of the institute, detailed studies of the influence of preliminary heat of fuel preparation on the nitrogen oxides formation were carried out. Coal dust, with varying degrees of metamorphism: berezovskiy lignite coal (Vdaf = 44.7 %, Ndaf = 0.8 %), ekibustuzskiy

The data obtained were used to develop a full-scale pulverized-coal burner design with prethermal treatment of fuel. In 1983-1984 this burner heat output of 60 MW has been implemented and tested on an industrial boiler TPP-210A. Further tests were carried out on other boiler units using the system for heating fuel in burners. All tests confirmed the feasibility of using these burners. In all cases it was possible to reduce nitrogen oxide emissions from 1200 and 1800 to 500 and 700 mg/m3 respectively at combustion of kuznetskiy lean and low-caking coals [3].

To further implement this technology on the boilers of various designs at burning coals of various grades is necessary to conduct additional studies, including by means of numerical simulations. In this paper the mathematical model and some results of thermal preparation coal combustion calculation are examined.

Mathematical model

The model of non-isothermal incompressible multi-component gas was assumed as a model of flow in combustion chamber. The gas flow in the studied problem is considered as established, thus all equations are written in the steady-state form. It is assumed that combustion gases consist of N 2 , O 2 , CO , H O and complex of volatiles VOL. The model includes the following equations: equation of continuity

m

^T ij - ^

^^{+V( p} v f H⁽%*-^{V f} ] ⁺ S i ,

where D is the molecular diffusion constant, Sc – turbulent Schmidt number, S – source term describing reactions;

equation of energy transfer

P + V( pv-h ).v((, +   W V

⁺ S ch ⁺ S R ,

S_ch , S_R are source terms describing, correspondingly, energy effect of reactions and radiation heat transfer.

The modified high-Reynolds k- ε model of turbulence (Chen k- ε model) is used to describe the turbulent characteristics of flow. The equations determining the kinetic energy of turbulence and its dissipation rate have a form (Chen and Kim, 1987):

+ V( pvk ) = vl (p + ! yv k 1 + G - pa^

^+V ( ^p v ^-k ) -^V[ ( ^{p + p} ) .. / |

2 V .2

+ C-G - C p — + C3 k k pk where G is the rate of turbulence generation:

t dUi G = T jJ,

5xj turbulent viscosity is determined as

= C kL

M t    ц Р _£

Reynolds stress tensor has a form t_    (U, duj   2

^T ’ " " t [ ( d x .* = - i "^{3 5} ’ ^{P k} J .

The empirical constants C µ = 0.09, σ _k = 0.8, σ_ε = 1.15, С₁ = 1.15, C₂ = 1.9, C₃ = 0.25 are given in the work (Chen and Kim, 1987). These constants are approved for a wide class of isothermal flows. The form of k- ε model is adapted for fully developed turbulent flows. In the near-wall region wall function are used to save computational resources.

Temperature of mixture T in each point of flow field is found using the known local values of enthalpy and mixture components content:

h= ∑hm(T)fm, m=1

where the dependencies of component enthalpy on temperature h_m(T) is described by polynomials of 5th degree.

The radiation is the dominant heat transfer mechanism. The modeling of radiant energy transfer is conducted basing on the P1 approximation of spherical harmonics for a grey medium (Siegel and Howell, 1992). The advantage of this method is easiness of its matching with methods of aerodynamics and heat transfer calculation realized in curvilinear meshes. The absorption coefficients were calculated using the weighted-sum-of-gray-gases model.

Calculation of volatile fuel components combustion is based on the use of global irreversible reactions between fuel and oxidant. To describe the reaction in turbulent flows with large mixing time used a hybrid model using the kinetic model and the eddy break up model to determine the reaction rate. According to this model as the resultant velocity is chosen the lowest from rates:

R i =- MIN ( R i , KIN , R i , EBU )

Coal Dust Combustion. The Lagrange method was used in the present work to model of coal dust motion. During the modeling, the main forces acting on a particle were the force of phases interaction (aerodynamic resistance force) and gravity force. As the coal particles moves, it is heated up and it undergoes a number of process: extraction of residual moisture and volatile components, combustion of volatile components and char. When the coal particle advances in the furnace, the reaction processes of vaporization, coal pyrolysis and char combustion are considered. The coal particle consists of four components: water, volatiles, carbon and ash. Vaporization of moisture from the coal particle is described by the diffusion-limited model. Coal pyrolysis is modelled by a simple, one-step mechanism and the volatile composition is assumed to be constant. The reaction rate of coal pyrolysis is taken from experimental data.

Char combustion is controlled by the chemical surface reaction and the oxygen diffusion to the particle. This model includes the factor η which describes the transition between the char combustion regime limited by the rate of oxygen diffusion and the regime is sufficiently limited by the chemical reaction rate. Char particles are considered to burn at constant density and variable size.

The diameter change of a particle follows:

d δ ₌ 2 _{* K}c d τρ _к s

K_S^C = β C_{O 2} (273/ T_g )* α K

^K 1 ₊     1            k . kin      k . diff

α k . kin α k . diff

α = α if α   > ηα

K k . diff         k . k i n      k . diff

^α k . diff ^{= Nu} δ ^{D D}

Nu = 2 + 0.22 Pe ^{0.66 D}

α k . kin .

= K_кe

- E / RT

к

ρ _k is the density of the char particle (kg m^-3); K_S^C is the char combustion rate (kg m^-2*s^-1); Nu_D is the diffusion Nusselt number; D is the bulk molecular diffusion coefficient (m²/s); α k , kin is the reaction-rate coefficient for a chemical reaction (ms^-1), α _k,diff is the reaction-rate coefficient for diffusion (ms^-1). ^,

The instantaneous burning rate of an individual particle is determined from temperature, velocity, and size information by solving the energy balance for the particle, assuming a spherical, homogeneous, reacting particle surrounded by a chemically frozen boundary layer (i.e., single-film model). Heat losses from convection and radiation are considered, as well as the effects Stefan flow:

m p C p dT p 4 π r_p ² dt

= εσ ( T r ⁴ ad - T p ⁴ ) + α conv ( T - T p ) + ^QH 4 π r_p ²

α _conv is the convection heat transfer coefficient:

α conv

Nu λ 2 r p

The correction to the heat-transfer equation due to Stefan flow is provided modification of Nusselt number:

-

-

Ре 37

Nu = 2 + ^P ₂ ^e - ₉ ³ ₆ ⁷ ₀ Pe

2 Pe Pe Pe

where Pe is a Peclet number, Pe is a modified version of the Peclet number (i.e., the ratio of the convective velocity of the net mass leaving the particle surface to the diffusive velocity of heat leaving the surface).

When char burn, heat losses from convection is much larger than that is predicted for not burning particles. In the model is used correlation coefficient Kcomb:

comb aconv

^ conv^comb

- 5000

T g

K comb   ^L^⁵ e

α c^co^on^mv^b , α conv – are convective heat transfer coefficients for burning and not burning coal particle respectively. Present model of coal particle combustion was validated in [4].

The influence of particles on the averaged gas motion, the gas components concentration and enthalpy was taken into account on the base of PSI-cell method proposed by Crow (Crow et al., 1977).

NOx Formation. In the process of NOx formation simulation three mechanisms are taken into account: formation of thermal NOx according Zeldovich’s model (Zeldovich, 1946), formation of prompt NOx according the Fenimore’s model (Fenimore, 1979) and formation of fuel NOx (Magel et al., 1996). Additional equations for NO and intermediate hydrogen cyanide HCN transfer are introduced:

P O + V ( p v f NO ) = V ( D Vf_№ ) + S no f N^ + V ( p v f _HCN ) = V ( D V f _HCN ) + S _HCN

The source term in the equation of NO transfer describing thermal mechanism (Zeldovich, 1946) may be written as

S thermal-NOx

=MNO

d [ NO ] dt

where d[NO]/dt is calculated as following:

d [ NO ] _ 2 [ O ] ( kk 2 [ O 2 ][ N 2 ] - k -1 k -2 [ NO ] 2 ) dt              к 2 ^[ O 2 ^] + к -1 ^[ NO ^]

Assuming the partial equilibrium for oxygen atom density [O], we obtain

[ O ] _ 36.64 T ^1,2 [ O ₂ ] 1/² exp ( -27123/ T )

Reaction rate constants (m3/(mol⋅s)) are equal k = 1.8-10s exp (-38370/T)

k -i = 3.8 - 10⁷exp ( -425/ T )

k ₂ = 1.8 - 10 4 - T - exp ( -4680/ T)

k -2 = 3.8 ^{- 1}0 ^- T ^- exp ^{( - 20 820/} T )

The prompt NOx forms in the presence of hydrocarbon radicals which prevail in fuels with high molecular H:C rate. The mechanism of prompt NOx formation was described by Fenimore (1979). Source term in the equation of NO transfer may be written

S

prompt - NOx

^M NO

d [ NO ] dt

d[NO]/dt is calculated according the expression:

d [ NO ]         a              ( E 3

= kpr [O21 [N2][VOL 1 exPI -NN I, dt                         RT

4        y

Oxygen reaction order a depends on flame conditions (de Soete, 1975).

The fuel NOx is a result of reaction between oxygen and fuel nitrogen. In the process of coal fuel gasification and char burn there takes place the transformation of nitrogen containing compounds to NH 3 (ammonia) and HCN (hydrogen cyanide). Depending on scheme of chemical reactions between these compounds and combustion gases, formation of NO or N₂ takes place.

Modified de Soete model (Magel et al., 1996), consisting of three global reactions, is realized to calculate the fuel NOx :

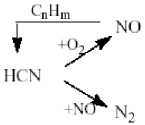
HCN- = - 3.5 - 10¹⁰ exp( - 3370/ T ) x_HCNx a _o

d' C' = - 3 - 10¹² exp( - 30200/ T ) x _HCN x _No dt

—NO = - 2.7 - 10 6 exp( - 9466/ T ) x_NOx_{c H}

n

Numerical algorithms. Conservation equations for gas phase are written down in a generalized conservation law in a control volume. For the volume finite-difference analog of equation is written down. For calculation of diffusion flow on the face of control volume centrally-difference scheme with second order precision is employed.

At the approximation of convective terms Leonard’s scheme is employed that is substantially minimizes the circuit viscosity. For connection velocity and pressure fields SIMPLE-C procedure is employed.

Results

Validation of the model was carried out on laboratory-scale plant of All-Russia thermal engineering institute. This plant consists of dust preheater in which coal is heated until specific temperature, burner consisting of two coaxial cylinder and combustor. Coal-gas mixture from a preheater moves on the internal flow path, air- on to the external. Original fuel compound is shown in Table 1. Coal and gas compound after preheater are shown in Table 1, 2. Experiments and numerical calculations are carried out with two coal sorts used: brown and black lean coals. The stationary plant is shown in Fig. 1.

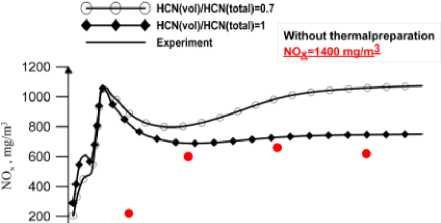
The calculation results for black coal are shown in Fig.2, 3. Fig. 3 shows concentration NOx along the furnace. One can see satisfactory agreement with experimental data at volatile nitrogen to total nitrogen ratio equal to one. In Fig. 4, 5 the comparison of calculated and experiment results for brown

Table 1. Coal composition

Black lean Coal
	W	A	C	H	O	S	N	V
Until	1.8	22.7	67.8	2.79	2.72	0.45	1.66	13
After	0.3	25.1	70.77	1.12	0.67	0.45	1.49	4.4
Brown coal
Until	10.4	4.84	59.5	3.81	20.34	0.34	0.76	45.7
After	0.2	7.78	77.57	2.94	10.21	0.37	0.83	18

Table 2: Gas composition, %

CO 2	CO	H 2	CH 4	N 2	O 2	NOx
15.8	10.6	6.6	0.9	61.2	0.5	0,005	Black lean Coal
26.9	18.7	5.1	1.52	44.7	0.3	0.016	Brown coal

Fig. 1. The stationary plant

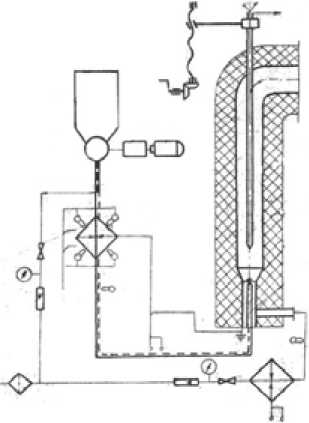
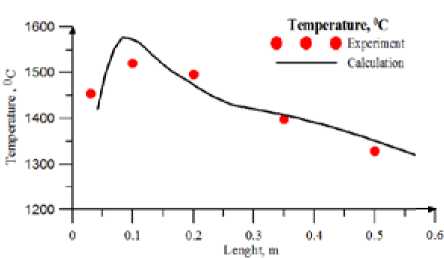
Fig. 2. Temperature (°C) Along the combustor (Black lean coal, Т tp =790 ºС)

Black coal (Ttp=790 °C, alfa=1.12)

NO,=750 mgfm1

1              1 I 1 I 1                            1

О 0.1        0.2       0.3       0.4       0.5       0.6

Lenght. m

Fig. 3. NO x concentration,(mg/m³). Along the combustor

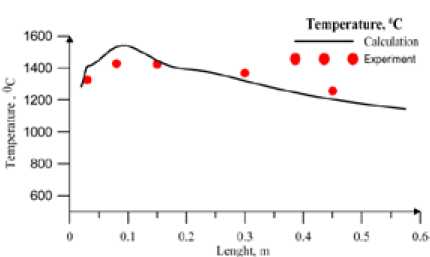
Fig. 4. Temperature (°C) along the combustor (Brown coal, Т tp =612 ºС)

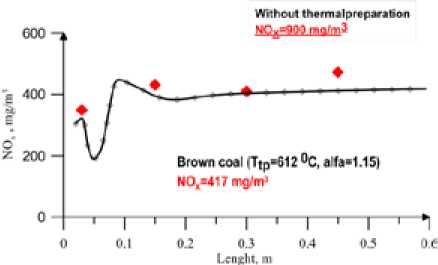
Fig. 5. NOx concentration,(mg/m3). Along the combustor coal. The profiles of the temperature and NOx concentration are generally in good agreement with the measurements.

For research heating, combustion coal and also influence of application of thermo-preparation concentration for decrease of nitric oxides the geometrical model of a burner consisting from muffle and furnace extension has been constructed. For research of initial development of a flame, and also, for the purpose of approach to real working conditions of a burner the limited area of combustion space was considered. The sizes of a burner are shown in Fig. 6. Computational grid of burner is presented in Fig. 7.

For calculation there was used black coal the structure of which is represented in Table 3. The analysis of the used coal is given in Table 4.

Fuel with grinding 30 micrometer and a part of primary air at the temperature 25 ºС is tangentially supplyed in to the an input 1 (Fig.6). In the cannel 2 supply of fuel (d=90 micrometer) and air at the temperature 120 °C. Secondary air at the temperature 300 °C is supplied into the cannel 3. Results of modeling in the form of distribution of temperature and concentration are resulted in Fig.8.

Then, with the aim to study the influence of use of burner with thermo-preparation on decrease of nitric oxides concentration on an exit furnace chamber, modeling of boiler PK-39-IIM (see Fig.10) was carried out. As the initial data for a boiler results of modeling of burner were employed presents above. Comparison was made with a basic variant of boiler without thermo-preparation. The temperature on

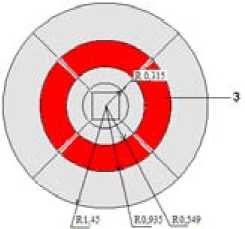
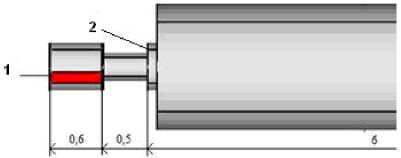
Fig. 6. Geometrical model, m

Fig. 7. Computational grid of burner

Table 3. Coal composition

Characteristic, %
Cr	43
Hr	2,7
Or	7
Nr	0,8
Sr	0,6
Ar	39,6
Wr	6,3
V daf	31,4
Qr i , kcal/kg	3917

Table 4. Operating conditions of the pulverized-coal combustion burner

Fuel rate, kg/s	2,08
Total air flow, m3/h	467640
Temperature secondary air, °C	300
Temperature dust air mixture	120
Excess air coefficient	0,812

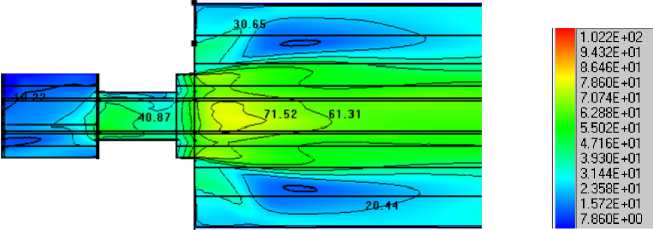
Fig. 8. Module of velocity, m/s

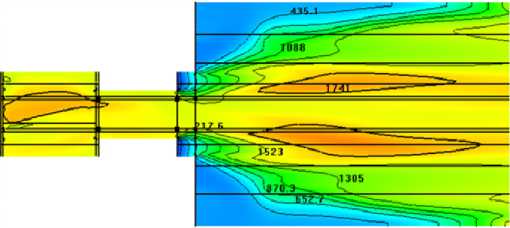
Fig. 9. Temperature distribution, °C

"21J^"с 3 2. О08Еч£3 1.841Е+03 ^ 1.506Е+03 1.33ЭЕ+03 1.172Е+03 1.004Е+03 8.368Е+02 6 694 ♦02

№ 5 .621 +02 _ 3.347Е+02 ■ 1.674Е+02

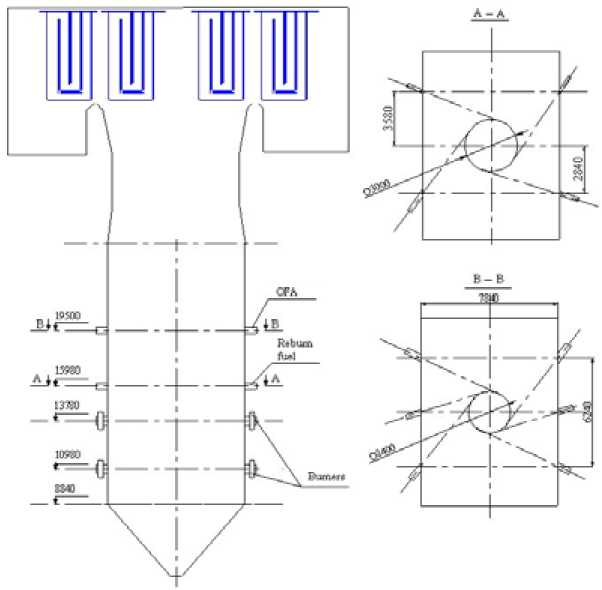
Fig. 10. PK-39-IIM scheme

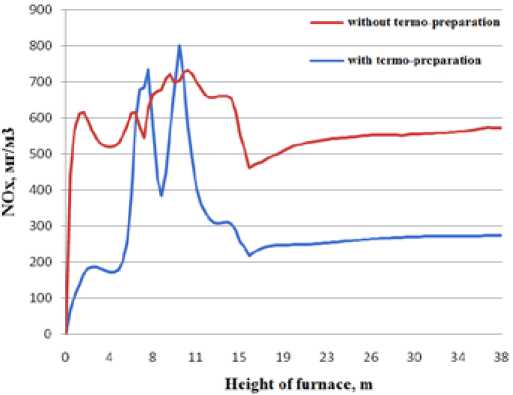
Fig. 11. The nitric oxides concentration upheight of furnace chamber an exit of furnace was 1167 °C. Unburned carbon 0.17 %. NOx concentration on an exit from furnace was 275 mg/nm3 (see Fig.11).

Conclusion

• 1.    Applicability of the burning thermal preparation coal mathematical model has been validated by comparing its predictions with the experimental data of a laboratory-scale pulverized-coal combustion burner. The results of the calculation show good agreement with the measurements.

• 2.    Numerical research of low emissive burner with step supply of air and preliminary heating coal dust was executed. As a results of calculation optimal sizes of a burner providing heating air-and-coal mixture have been found. The given warming up provides an intensive exit of flying that give the chance to lower nitric oxides concentration on an initial site of a flame.

• 3.    On the basis of the data received at the modeling of low emissive burner modeling of boiler PK-39-IIM with thermally prepared fuel was carried out. Application of the given technology of preliminary heating coal dust provides to reduction of nitric oxides concentration in combustion products to level of 275 mg/nm3.

Acknowledgement

This work was supported by the Ministry of Education and Science of the Russian Federation. government contract № 14.A18.21.1962 and Russian Foundation for Basic Research (Grant № 14-0801079).