Numerical investigation of the problem of cohesive running soils punching shear

Let us consider a sample of material (soil) with different strengths occupying a plane domain W with the boundary , consisting of three non-intersecting parts u, p and up, with displacement vector u = u1,u2) being set on the first part, a vector of distributed external force p = p1, p2) being set on the second one, and mixed-boundary conditions being set on the third part: in the absence of the displacement of the bound points in the direction of the normal the tangential stresses have been fixed un =u⋅n=0,                      (1)

where n = n ₁, n ₂ ) and τ = τ₁,τ₂ ) are normal and tangential vectors to the boundary, P_fr is the given function modeling friction.

The problem is to define vector displacement field u and tensor stresses field σ, satisfying boundary conditions u = 0 at Γu , un = 0 at Γup , to the equilibrium equation in variation form:

JJ g : s U<) ) d Q =

Ω

= J p ■ йd y+ J pfr ■ й_т d Y             (2)

Г        Г p          up for any vector field й, satisfying homogeneous boundary conditions in displacement at     and    . Here u            up

2ε ( u ) = ∇ u + ( ∇ u ) is the deformation tensor, corresponding to the vector field u (asterisk means transposition). Besides, determining equations must be carried out in Ω domain. With the help of them it is possible to determine stresses tensor according to the given deformation tensor in every point of domain Ω.

Mixed-boundary conditions on the section _up appear, for example, at the modeling of the process of the materials punching through the die with rigid bounds. In this case, the value P_fr presents friction stress equal to zero if the die surface is perfectly smooth.

For the description of deflected mode of the materials with different strengths, having special ultimate strengths under tension and compression, we will use the model of granular material with plastic couplings [1]. Under the action of compressive or stretching stresses, which are less than engagement coefficient (ultimate strength of the couplings) such materials are not deformed. The attainment of the ultimate strength corresponds to equilibrium condition, at which deformation may be an arbitrary positive quantity. Stresses above this limit are impossible. Regulated determining deformation relations of the materials with different strengths, taking into account the particles and binder elasticity, are given in the equations system

σ= a : ε-     a :Πε- a ^{- 1} :σ

1+λ              0

where σ is the stress tensor, σ₀ is the engagement tensor, a is symmetric positively determined coefficients tensor of the particles elasticity, λ is the regularization parameter, is the projection operator to the c one of a llowable deformations according to the norm ε = ε: a :ε.

In the model of granular material with absolutely rigid particles the determining relations of which are obtained from (3) in the limit of a →∞, λ→0 , the stress potential is equal to σ₀ : ε+ δ _C ε ) , where δ _C ε ) is the indicator function of cone, equal to zero on the cone and equal to infinity outside this cone. The dual deformations potential δ K σ-σ0 ) is expressed in terms of the indicator function of the conjugate K cone, which is composed of stress tensors, subtending obtuse angles with tensors of cone in the scalar product sense, given by the contraction σ: ε [2].

Computational algorithm . The main idea of the algorithm is the change of determining equations (3) by iterative formula ( n =1,2,3, K )

σ ⁿ = a : ε ⁿ - a :Πε ^{n - 1}- a ^{- 1}:σ 1+λ                 ^{0 )}

or

ε ⁿ u ⁿ ) = a : σ ⁿ +Δσ ^{n - 1} ) ,

• a : δ σ ^{n -1} =π -1 c : a ^{- 1} : ε ^{n - 1} ( u ^{n - 1} ) -σ    .⁽⁴⁾

c ⁰

At the first stage the initial stress field Δσ ⁰ is identically zero: the elastic problem for unstressed material with the tensor of compliance modules a is solved. At the following stages, initial stresses are calculated through the field of deformations obtained by the previous solution. Iterations are continued until the difference norm of two approximate solutions at the adjacent stages becomes less than the preassigned calculation accuracy.

The task at the n stage of the algorithm is reduced to the

minimization of the integral functional

( 1 + ^X)|| a : (Ag ■ -Ag ” ) |0 =

In (u ) = J

Q

I ^{s( u} ' 2 -1

^^^^^^

Ag n ^{- 1}

)

s ( u ) d Q-

Iⁿ a -' ( ^E ( u n ^-' ) ^- a : G o ) ^-n a - ( s ( u ) - a : G o ) |0 ^{- -}| s ( u" ^{- 1} " u ' Io =|| u" ^-1 - u l-

-J p ■ udГ + J pfr ■ uTdу Г p              Г up or to the numerical solution of the variational equation

Thus, the estimation is given by

un

-

u - ¹ 1 + X

n - 1 u^{n 1}

- u

11- (1+X)"

u ⁰ - u

1 ^,

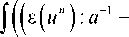
Q

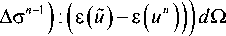
which guarantees the convergence of iteration sequence to

= J p■(й-un)dГ + J pr ■(йт -uTn)dY, Г p                         Г up u,un e U,

the exact solution with a speed of geometric progression with denominator ^(1 + X ) <  1.

Numerical experiment . As an example let’s consider a

for which the standard technique of the finite-element method is applied [3, 4]. As it usually is, the displacement space U is approximated by finite dimensional subspace U_h ( h is a typical digitization parameter), strained on the given system of base functions from U space. As a result, the finite-dimensional task of quadratic programming, which results in the large-scale system of linear algebraic equations, is obtained. In the specific calculations given below the standard piecewise-linear splines defined on the irregular frame were selected as an alternative to base functions, and a system of linear equations has been solved by the conjugate gradient method. The convenience of this technique lies in the fact that it sufficiently simply allows to realize the programming technology at which only non-zero coefficients of the system matrix and indexes corresponding to them, that is, lines and columns, are constantly stored in the computer memory [5].

Exact problem solution, minimizing functional I (u ) on U space, evidently, satisfies variational equation (5) with the change of stress Ag ^{n - 1} for the stress

plane deformed state of the homogeneous sample with direct bounds, the uniformly distributed pressure P = (0, - p ₀ ) , (p ₀ >  0 ) operating at its upper boundary (fig. 1).

The field for shear intensity

2       2 2₂ 2₂₂

^Y(s) = v3 ^(s 1 ^-s 2 ' ⁺ 3 ^s 1 ⁺ 3 ^s 2 ^+Y 12 ,

where е = (б1,82, Y12), is shown in figure 2, a. It was obtained on the basis of classical theory of elasticity. In figure 2, b itisshownonthebasisof the model of the material with different strengths with an internal friction parameter, corresponding to the firm ground. The intensity increases from white colour to black one in linear dependence.

Ag ” = a ¹ : П c -1 ( c : ( a ¹ : s ( u ) -g ₀ ) ) .         (6)

Having substituted exact solution u to the equation (5), as a varied element u and an approximate solution u n to the similar equation with Ag” , after results summation we will obtain

J^| s ( uⁿ - u )| 1 -( Ag ^{n 1} - Ag ” ) : s ( uⁿ - u )) d Q = 0 .

In terms of scalar product

( s , s ) = J s : a ^{- 1} : s d Q

Q __ and appropriate Hilbert norm ||s||o = ^(s, s) the last equation can be presented in the form of

||s( u - u )||o = ( a : (ag n-1 -Ag”) , s (un - u )^, from where by Cauchy-Bunyakovsky inequality we have

I ^s ( ^u n ^{- u} >1L -I a ^: (^{Ag n - 1 -}М1L-          (7)

Let us assume for simplicity that a = X b , c = ( 1 + X ) , where l is a small dimensionless parameter.

Under Corn inequality, the left part (7) determines the norm || uⁿ - u || on U space, equivalent to the H ¹ ( Q ) norm. The right par ¹ t is estimated with the help of (4) and (6) formulas, taking into account that the projection operator is a non expanding map:

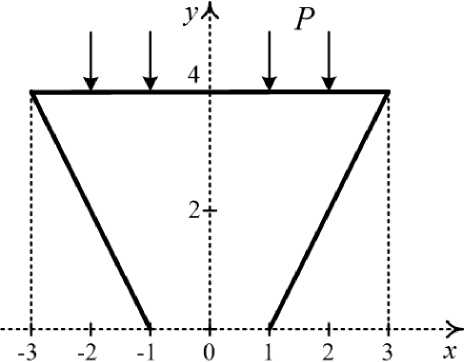
Fig. 1. The loading condition of the sample

By comparing the figures we can see that a conical inrush zone is formed in the soil with different strengths in the lower part of the sample.

The punching problem with the application of non uniformly distributed force to the upper area boundary has been considered as well: the load decrease from the centre to the lateral bounds occurs uniformly (fig. 3). The field of shear intensity obtained on the basis of the classical theory of elasticity is shown in figure 4, , and the field of shear intensity obtained on the basis of the model of the soil with different strengths is shown in figure 4, b .

Comparing figure 4, a with figure 2, b we may draw a conclusion that the external pressure redistribution with the same integral value of the force influences the change of the deformed state in the lower part of the sample weakly.

In figure 5 we can see the loading condition in the problem concerning the sample punching through the die with concave side bounds. The P force is distributed along the upper bound of the sample uniformly.

a

b

Fig. 2. The intensity of shear deformation

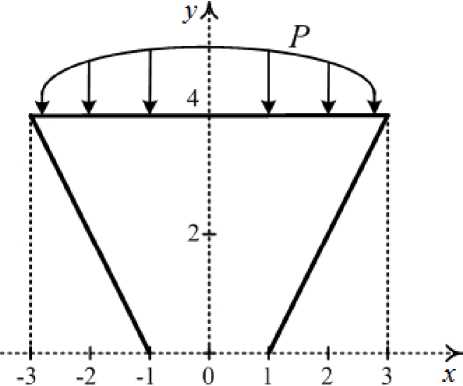
Fig. 3. The loading condition of the sample

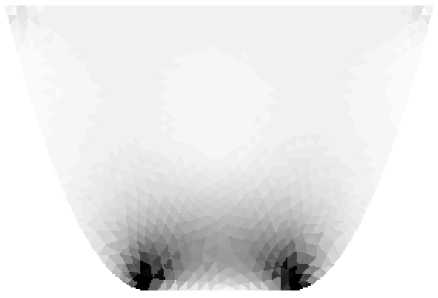
The field of shear intensity obtained on the basis of the classical theory of elasticity is shown in figure 6, a , while in figure 6, b it is shown on the basis of the model of the materials with different strengths.

In comparison with rectilinear lateral bounds in the case of concave bounds the redistribution of strains localization zones occurs both in elastic materials and in materials with different strengths. The size of the inrush zone essentially increases.

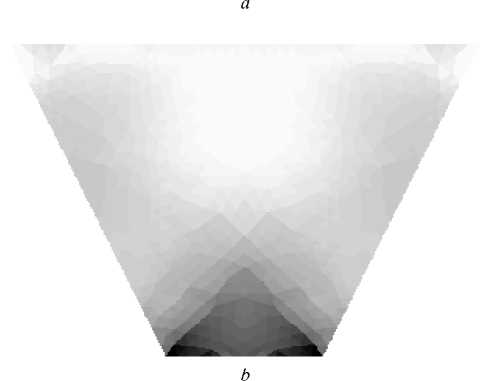
Fig. 4. The intensity of shear deformation

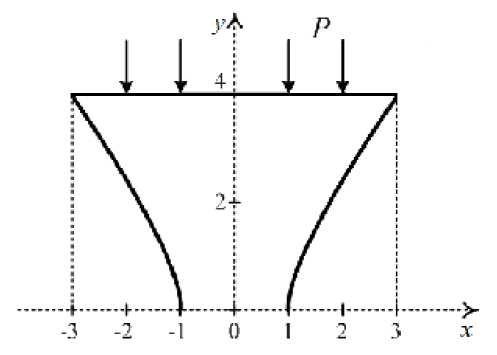
Fig. 5. The loading condition of the sample

Further the problem of punching of the sample with convex side bounds was considered. The loading condition schemes for uniformly and non uniformly distributed P force are shown in figure 7 and figure 8.

The field of shear intensity for the problem shown in figure 7 obtained on the basis of the classical theory of elasticity is presented in figure 9, a , but in figure 9, b it is shown on the basis of the model of the material with different strengths.

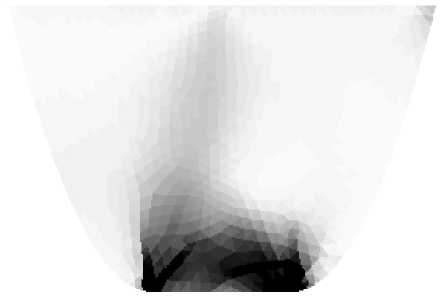
The field of shear intensity for the problem shown in figure 8, obtained on the basis of classical theory of elasticity is presented in figure 10, a, but in figure 10, b it is presented on the basis of the material with different strengths.

By comparing figures we can notice that as a result of pressure redistribution there appears an additional line of strains localization corresponding to the asymmetric statements of a problem.

b

Fig. 6. The intensity of shear deformation

a

b

Fig. 9. The intensity of shear deformation

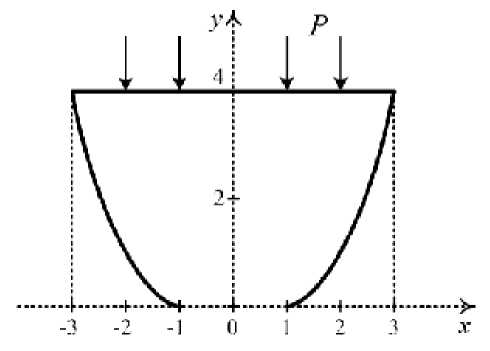
Fig. 7. The loading condition of the sample

a

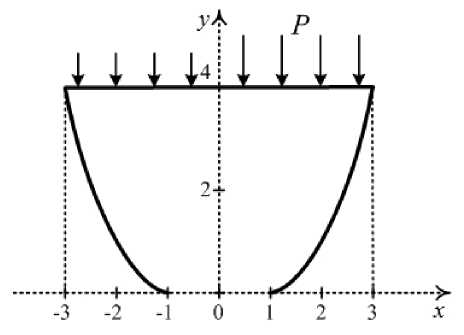
Fig. 8. The loading condition of the sample

b

Fig. 10. The intensity of shear deformation

On the basis of finite-element method the computational algorithm for the solution of problems of strains localization in the materials with different strengths has been suggested in the paper. The plane deformed state of the sample of the material with different strengths at punching through the die with convex and concave lateral surfaces has been considered as an example. The advantages of the suggested algorithm in comparison with a classical approach to the elasticity theory are most pronounced during the solution of problems in asymmetric statement.