Numerical methods in assessing the reliability of spatial metal structures with a high level of responsibility

The basic basis for ensuring the reliability of structures at the design stage in the engineering practice of the last decades was the use of limit states method, implemented in the vast majority of specification documents on the design of structures of both Soviet and post-Soviet period. Thus, alongside with the positive aspects of the application of this method its drawbacks are well-known (semiprobabilistic basis, impossibility of ensuring the given level of reliability for identical structures designed of different materials, primitive accounting of the time factor and the level of responsibility of the designed structures, etc.). And if for application of well-established constructions for wide use such approach gave a stable positive result. Last years the deviation from practice of the standardized design together with a tendency of increasing parameters of designed objects, complication of structural forms, application of new materials unfortunately leads to increasing of a quantity of failure events of buildings and constructions, including facilities of a high level of responsibility [1–5]. Lately increased level of terroristic threat in our country has undoubtedly added to these factors [6–12]. The creation of specification documents of a new generation in which the questions of ensuring the reliability of framings are solved at the next level, when designing the constructions of a high level of responsibility it is required not only to provide a guaranteed level of reliability of framings but also to protect them from a possibility of a progressive (progressive) destruction should meet these challenges [13–15]. At the same time, a detailed study of the basic documents regulating the calculation for progressive collapse, for example [16], leaves a number of questions which have no clear and unambiguous recommendations [17–21]. One of these issues is the principle of choosing the most critical element, the removal of which can lead to the development of progressive collapse, for complex repeatedly statically indeterminate systems [22]. In some cases, the mechanism of application of coefficients of dynamics when collapse simulation ("emergent") of an element occurs is not clear. All these review questions require further clarification and refinement in the future.

Based on the above, we can say that a clear algorithm for determining reliability indicators for constructions of increased responsibility is needed. An unambiguous methodology is needed to determine the most critical construction elements for further analysis of the propensity of the system to progressive collapse.

• 2    Materials and Methods

Within this study, the authors propose a methodology that allows to determine such a rod element or a group of the most critical rod elements of the construction, the complex failure of which can initiate the beginning of a progressive collapse. And when analyzing reliability indicators, the key point of the developed approach is the hypothesis that for a multiple statically indeterminate rod system, the variability of properties of this very group of elements in combination with the indicators of variability of loads and influences will largely determine the level of reliability (failure probability) of the construction in whole. Naturally, that the indices of calculation results are applicable to the analysis of a particular design model, and for the full substantiation of the reliability level of the designed system it is necessary to apply sequentially the algorithm stated below for all design situations, regulated by the used design codes of metal constructions.

The first stage of the analysis is to establish a set of key structural elements, their failure initiating the development of progressive collapse. To determine such an element (or a set of elements) it is necessary to make geometrical and structural nonlinear analysis. Its essence lies in additional step-by-step loading of the structure with the imposed load. The elements of the system being the first to fail (no longer meeting the requirements of the first limiting state) will be the most essential ones. The load is applied in increments of 1/10-1/50 of the effective characteristic value. The background of the software package implementing the proposed methods is the finite element method (FEM) accomplished in geometrical and structural nonlinear formulation. The finite element model for the rod is shown in Figure 1. At each loading step, the analysis in deterministic formulation is carried out considering the stressstrain state of the previous step. In this case, the geometry of the structure is updated (structural deformation design analysis) and the components of the stiffness matrix of the structure are adjusted based on the use of correction functions considering the influence of the working stresses in the elements accumulated during the previous stages of the analysis. Correction functions are introduced at the stage of forming local stiffness matrices of elements (Fig. 2, Table 1) and are formulated based on the approaches outlined in the papers by Novozhilov V.V. and Kornoukhov N.V. [23, 24]. As one can see, the type of the expression used depends on the sign of the effective longitudinal force in the element in question, and the applied hyperbolic operators allow us to significantly increase the rate of convergence of analytical results (similar approaches are used in some programs for the design analysis of cable-stayed bridges). The matrix of correction functions is shown in Figure 3. The resulting local matrix for the stiffness of a rod element is obtained by element-by-element multiplication of the original stiffness matrix (Fig. 2) with the correction matrix (Fig. 3).

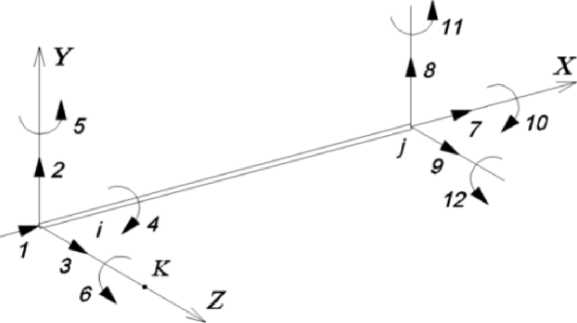
Fig. 1 - The final element of the spatial rod

ЕА L	0	0	О	О	О
0	12ЕЬ о L1 0		О	О -^ ° Lz
0	0 ^ и L3			& L1 °
0	0	О	GU L	О	О
0	О f		О	f О
0	-f О		О	О f
_ЕА L	О	О	О	О	О
0	-f О		О	л 6ЕЬ О ^2
0	О -f		О	-f О
0	О	о -	GI кр L	О	О
0	о -^		О	f О
0	6Ек L1 О		О	0 f

ЕА ~ L	О	О	О	О	0
	12Eh				6 Eh
О	1?	О	О	О	Lz
О	О	12Е1у Is	О	6Elu " L1	0
О	О	О	Glm " L	О	0
О	О	6Е1м ' L2	О	2Е1» L	0
	6Е1=				2EL
О	Lz	О	О	О	L
ЕА
L	О	О	О	О	0
	12EI,				6Eb
О	L3	О	О	О	L2
О	О	12Е1и	О	6Е1у	0
О	О	о	ulup L	0	0
О	О	6ЕЬ L5	0	4EL L	0
	6Ек				4Ek
О	е	О	0	0	L

Fig. 2 - Stiffness matrix of a spatial rod element in the local coordinate system (EA - longitudinal stiffness, EIy, EIz - bending stiffness, GIkr - torsional stiffness, L - design length of the rod)

s5e   О    О    О    ОО

О  з1е   О    О    Оs2e

О    о  sz1e  о  sz2e

ОООООО

О    0  sz2e  о  sz3eо

О  s2e   о    О    0зЗе з5е   О    О    О    ОО

О  s1e  о    о    0s2e

0    О  sz1e  0  sz2eО

ОООООО

О    0  sz2e  0  sz4eО

О  s2e   о    О    0s4e

s5e   О    О    О    ОО

О   s1e   о    о    оз2е

О    0  sz1e  0  sz2eО

ОООООО

О    0  sz2e  о  sz4eо

О   s2e  о    О    Оз4е s5e   о    О    О    ОО

О   Sie   О    О    0з2е

О    0  sz1e  о  sz2eо

ОООООО

О    о  sz2e  о  sz3eо

О s2e ООО зЗе

Fig. 3 - Matrix of correction functions

Table 1. Correction functions

Tension rods (paxl>0)	Compression rods (paxl<0)
phi3×sinh s1e=          ; 12×rt	phi3×sin(phi) s1e=              ; 12×rc
phi2×(cosh-1) s2e=               ; 6×rt	s2e= phi2×(1-cos(phi)) ; 6×rc        ;
phix(phi х cosh-sinh) s3e=                      ; 4×rt	phi х (sin(phi)-phi х cos(phi)) s3e=                             ; 4×rc
phi×(sinh-phi) s4e=               ; 2×rt	phi×(phi-sin(phi)) s4e=                   ; 2×rc
s5e=     EF×rtm ; 1 4×paxl3× l 2	1 s5e=      EF×rcm ; 1 + 4×(-paxl)3× l 2
zphi3×zsinh sz1e=             ; 12×zrt	zphi3×sin(zphi) sz1e=                ; 12×zrc
zphi2×(zcosh-1) sz2e=                 ; 6×zrt	sz2e= zphi2×(1-cos(zphi)) ; 6×zrc
zphi х (zphi х z cosh-zsinh) sz3e=                          ; 4×zrt	zphix(sin(zphi)-zphi х cos(zphi)) sz3e=                                 ; 4×zrc
zphi×(zsinh-zphi) sz4e=                  ; 2×zrt	sz4e= zphi×(zphi-sin(zphi)) ; 2×zrc

rt=2-2×cosh+phi×sinh;			rc=2-2×cos(phi)-phi×sin(phi);
zrt=2-2×zcosh+zphi×zsinh;			zrc=2-2×cos(zphi)-phi×sin(zphi);
1       ..Г 1 7. rtm=phi х em1 x--+ phi x ----1 -2 x tanh       (sinh) V                    7			Г 1/                /    .    x27 _                 / sin(phi) , . • |      1      |0 rcm=phi x em1 x  ----——- + phi xl-------1 -2 x cos(phi)         V sin(phi) J V                              J ,             Г          1/. 1                        sin(phi) x em2+2 x phi x------x em3 x 1 + phix----- —- ; sin(phi)                  cos(phi) V                  J
x em2+2 x phix / x em3 x| 1 + phix —— sinh         V        tanh		7 ’
			Г                     Г 1         7 zrcm=zphi xzem1x    sin(zp   +Zphi x l-------- -2 x cos(zphi)         V sin(zphi) J V                                J 1                  Г xzem2+2xzphix-------xzem3x 1+zphix /sin(zp 0 ; sin(zphi)                   cos(zphi) V                    J
zrtm=zphixzem1x —i—+zphix —i | ztanh         V zsinh 7		-2×
V                          7 xzem2+2xzphix —J— xzem3x | 1+zphix —J— | ; zsinh         V         ztanh J
ePh - e ( - Phi) sinh=               ; 2			–
ephh + e( - Phi) cosh=             ; 2			–
ePh - e( - Phi) tanh=              ; ePPh + e( - Phi)			–
e zPh - ( - zPhi) zsinh=               ; 2			–
zphi + ( - ZPhi) zcosh=              ; 2			–
ezPph - e( - ZPhi) ztanh=               ; e zPh + e ( - ZPhi)			–
N fin -N in paxl= 2    ; phi= em1=M 3 in 2 + M 3 fin 2; ei zem1=M 2 in 2 + M 2 fin 2; N fin - axial force at the en stiffness relative to the M 2 fin - bending moment axis 2 at the beginning M 3 in - bending moment	paxl -----x l ; zphi= EI 2 m2= ( M 3 in + M 3 f zem2= ( М 2 in + M d of the rod; N in - specified axis 2 relative to axis 2 f the rod; M 3 fin - relative to axis 3	paxl ,-----------x l ; EI 3 2 n ) ; em3 M 3 in x M 3 fin ; 2 2 fin ) ; zem3=M 2 in x M 2 fin ; axial force at the beginning of the rod; EI 2 , EI 3 - bending or 3; EF - tensile-compression stiffness; l - rod length; at the end of the rod; M 2 in - bending moment relative to bending moment relative to axis 3 at the end of the rod; at the beginning of the rod;

In order to make a structural nonlinear part of the analysis, the load-carrying capacity of each element of the system is analyzed at each stage of loading. If an element fails, it is excluded from the design model, resulting in the so-called secondary design model. Its analysis is performed in a geometrical nonlinear formulation previously described. In this case the compressed rods are simply removed from the structure, and instead of the removed stretched rods, the internal forces acting in the element are applied but with the opposite sign (the validity of this methodology is considered in the papers by Streletsky N.S. [25]).

If the rest of the structural elements continue to meet the strength requirements due to the redistribution of the internal forces of the excluded rod, it is a sign of the stabilization state, the process of step-by-step additional loading of the structure continuing. An indirect characteristic of the quality of the design model under analysis is the number of such intermediate states: the more "stabilization states" there are, the less the system is prone to progressive collapse. The block diagram of the algorithm for determining the most critical elements and the tendency of the system to progressive collapse is shown in Fig. 4.

At the second stage of the calculation , it is necessary to determine the numerical value of the reliability index of the analyzed system. Herewith, as already noted, the probability of failure of the system as a whole will lie in the range between the probability of failure of one and the most critical element, and the probability of failure of a group of elements that initiate the onset of a progressive destruction, determined from the results of the first stage of the calculation.There are various methods for calculating the reliability of building constructions. The most common of them are given in [26-31]. In this study, the reliability of constructions is calculated by considering stochastic quantities as random numbers. A sufficient amount of statistical data is assumed to generate random numbers. Methods of working with a small volume of statistical data are not used [32, 33].

Speaking about the classical approaches to assessing the reliability of a single element, it should be noted that in the general case, the condition for failure-free operation in the technique of random variables is usually written as:

--^-'                     ******                    *****

Y ( t ) = R ( t ) - 5 ( t );

R ( t ) - generalized bearing capacity of a structure or element (in most cases, a random value of the yield strength of steel); S ( t ) - generalized load on the structure (in most cases, a random variable stress (force) from external influences); Y ( t ) - safety margin characteristic (bearing capacity reserve).

Then, under the condition that random variables correspond to the normal distribution law, the probability of failure of a structural element is calculated by the formula:

1   ? -?l g^g I              в - —

P f = P ( g <  ⁰ ) = I e ^{2 1} g ^J dg = 7- ' J e ² dg = у- ^ф ( в ) ;

gg2n -”            2 У2П о

5 ( 1 )

Ф (β) – Gaussian probability integral; g - the number of standards that fit in the range from g =0 to g = g ; в - safety feature.

в =

g = R - Q _;

^g  T R ^+ IQ ² ’

while: g = R - Q ; g > = ^ iR ² + Q ) ² ; -, n - mathematical expectation, standard value; R end Q - two mutually independent random variables ( R = R ( t ) ; Q = S ( t ) ).

The proposed random variables are the random level of stresses in the rods of the structure and the yield strength of steel [34]. Stress in structural elements is a complex random variable that may depend on such stochastic factors as: atmospheric loads [35], geometrical characteristics of sections, Mushchanov, V.; Orzhekhovskiy, A.

Numerical methods in assessing the reliability of spatial metal structures with a high level of responsibility;

foundation settlements, structural shape imperfections obtained during installation and operation, etc. With this formulation of the problem, the most appropriate method for determining the probability of failure is the Monte Carlo method [36–38].

START

Creating a design model of the structure

Entering the maximum allowable number of elements excluded from the construction (n)

Сonstruction calculation for maintenance and limit loads

Calculation of the stress-strain condition of the structure taking into account geometric nonlinearity (Novozhilov V.V. functions)

Loading with an additional load and calculation of the stressstrain condition of the structure taking into account geometric nonlinearity (Novozhilov V.V. functions)

Estimation of the supporting capacity of the rods (Ϭ≤R)

Removing elements that do not meet the conditions of the first limit state

Do not exclude from the structure

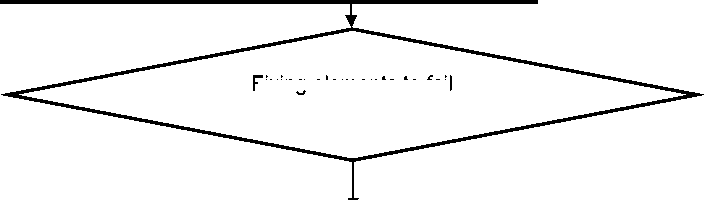
Fixing elements to fail

Not excess (n)

Excess (n)

Updating the geometry of the structure (adding displacements to the coordinates of nodes)

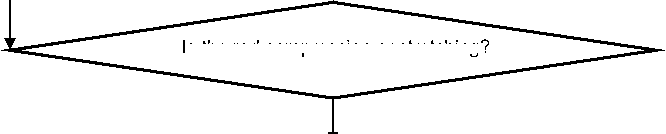
Is the rod compression or stretching?

Stretching

Сompression <

Exclusion of an element from the construction

Application to the nodes of the rod of reactions with the opposite sign

Updating the geometry of the structure (adding displacements to the coordinates of nodes)

Selection of elements that determine the reliability of the structure

Output of results

STOP

Fig. 4 - Block diagram of the algorithm for determining the design inclination to progressive collapse

Then the implementation of the second stage of the developed algorithm for calculating the determination of the reliability characteristics of an element or a group of elements can have the form shown in Figure 5.

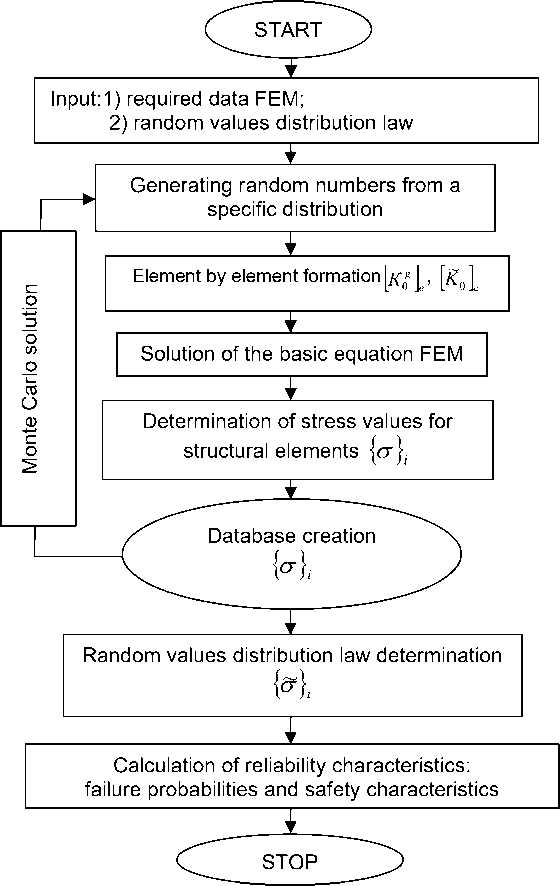
Fig. 5 - Block diagram of the algorithm for determining the reliability characteristics of the structure

Thus, the application of this approach in the engineering practice of repeatedly static design of high-level rod systems allows establishing the upper and lower limits of the reliability indicator of the designed system. Thus, under the «lower boundary» we can understand the level of reliability of one key element, which is not allowed to fail in accordance with the requirements of most existing normative documents, although the load capacity of the system as a whole is not exhausted. The «upper boundary» means the level of reliability of the whole group of key elements determined by the results of the first stage of analysis, the failure of which triggers the process of progressive collapse. The peculiarity of this definition is the use of the parallel compound model in calculating the reliability indicator, as well as consideration of the degree of interdependence of the given pair of elements in the computation process [39].

• 3    Results and Discussion

The technique described above is implemented in the MATLAB programming language. The software product allows you to assess the tendency to progressive collapse and calculate the reliability indicators of spatial metal constructions made of rods. For the convenience of downloading the initial calculation data, a software block has been created that allows automatically reading this information Mushchanov, V.; Orzhekhovskiy, A.

Numerical methods in assessing the reliability of spatial metal structures with a high level of responsibility;

from the files of the LIRA-SAPR program. This allows you to make verification calculations at the first stage of calculations.

Most load-bearing metal structures are spatial systems. To implement a visual example of the calculation, it is possible to apply any statically indeterminate construction. The required level of reliability of the vast majority of standard designs is fully provided by the methods of limit states using reliability coefficients. The interest is aroused by difficult constructions of increased responsibility. The least studied, from the point of view of the tendency to progressive collapse, are many times statically indeterminate systems with parallel operation of a large percentage of elements. These criteria are fully met by plates made of rods or structural constructions. They are used to overlap significant spans and create a large amount of usable space. These constructions have a number of undeniable advantages over other structural types of coatings. The main ones are the speed of assembly and installation, relatively low weight, aesthetic appearance. The authors settled on a constructive system of the MARCHI type. It has received a wide geography of application in the country and abroad, has proven itself positively during operation, and also has a localized assortment of cross-sections of elements.

Let's consider an example of using the proposed technique on a structural structure of the MAI (Moscow Architectural Institute) type with dimensions of 24x24x3 m. The structure is based on a rigid contour with attachment points along the upper belt (Fig. 6). The snow load [19] and its own weight act on the structure. Conventionally, the structure is located in the city of Donetsk. The mass of a square meter of the enclosing structure is 40 kg. Considering these parameters, the concentrated force acting into the node of the upper coating belt was 17.64 kN. The load increment step is 0.5 kN. The stiffness of the elements is selected based on the requirements of durability. Based on the results of the calculation of the first iteration, 200 rods were identified that failed at the second step of applying an additional load (Fig. 7). Analyzing Figure 7, we can note the obvious tendency of the system to progressive collapse. The cross sections of the marked rods are increased by one position of the pipe assortment used (from 38x4 to 63.5 x3). Let's repeat the calculation. After two stages of recalculation of the construction (based on the results of the calculation of the third iteration) (Table 2), with an increase in cross sections, we get two rods of the lower belt flying out of work at the sixth step of applying additional load (Fig. 8). The order of the elements leaving work at the third iteration is given in the form of a histogram (Fig. 9).Two stages of system stabilization are observed. At step 6 (after the departure of 2 rods) and 7 (after the departure of 26 elements). Then a progressive collapse begins.

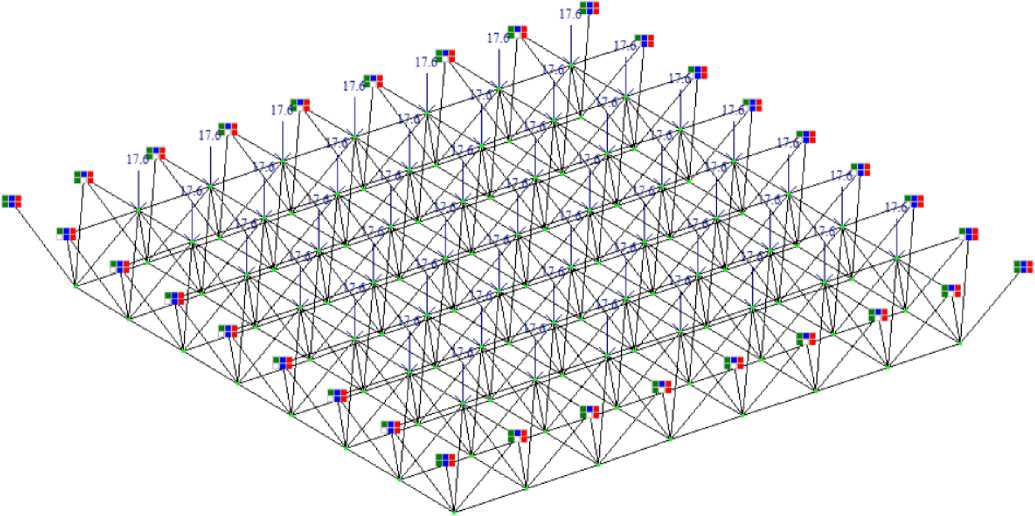
Fig. 6 - The initial design scheme of the 24x24x3 m structural construction in the LIRA-SAPR software package

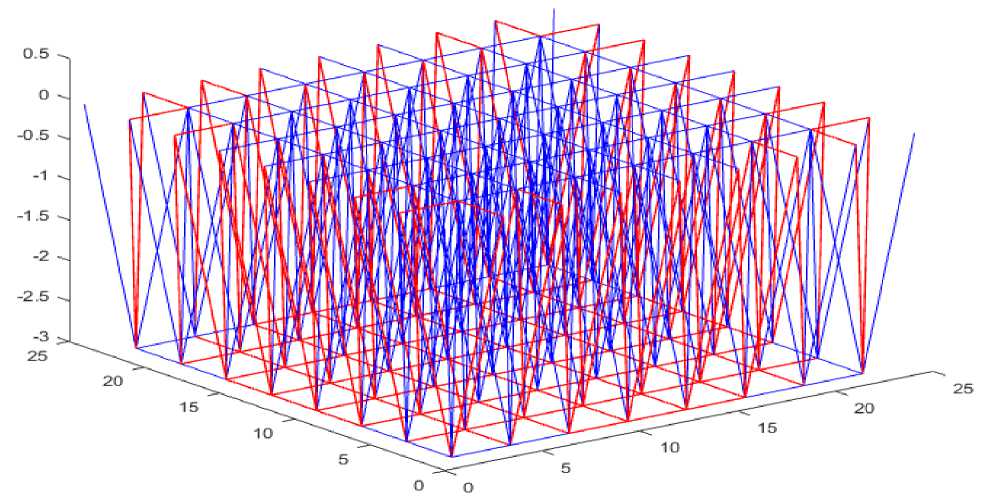
Fig. 7 - Rods out of operation at the second step of the application of additional load of the first stage of calculation

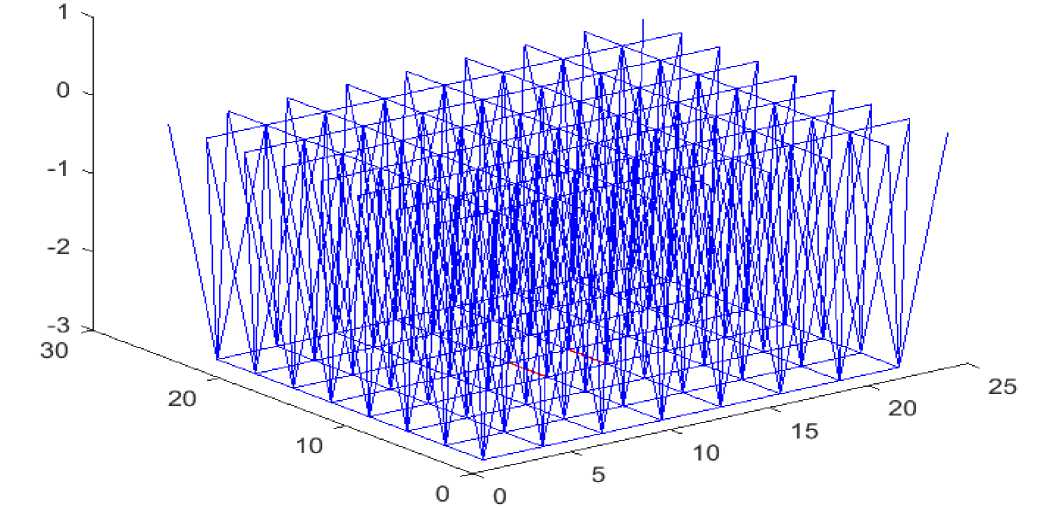
Fig. 8 - Rods out of operation at the sixth step of the application of additional load of the third stage of calculation

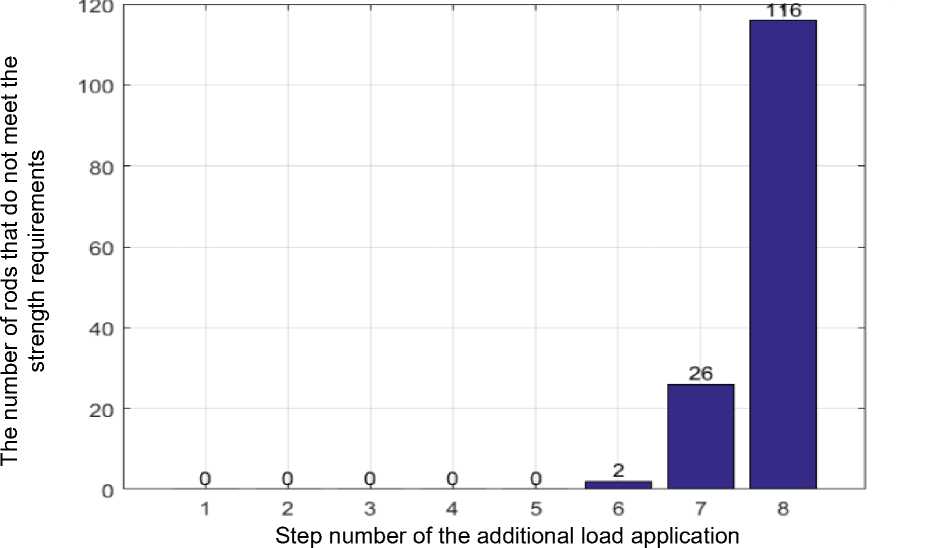
Fig. 9 - The graph of the output of structural elements at each step of the application of additional load of the third stage of calculation

Table 1. Calculation of the coating reliability characteristic (β)

с о го ф	ч— С О ф с/) — е СО     с о .О ф О о ® ф ф т £	Structural elements	The number of elements that failed before the system was stabilized	β min	β max	с ^ о (/) О Е
1	2	3	4	5	6	7
1	63.5х3	support elements of the upper belt	0	-1.54	-1.36	6.14
	38х4	upper-lower belts, grid	200
2	63.5х3	supporting elements of the upper belt	40	0.51	1.14	7.21
3	63.5х3	upper-lower belts, grid	2 lower belt	2.67	2.67	7.52
	76х3.5	lower belt	0

Table 2 shows the sections of the elements (column 2) and where in the construction they are located (column 3). Column 4 shows the number of elements that failed during the considered iteration and indicates where they are located. These rods will be the group of the most responsible elements. The reliability of which characterizes the reliability of the entire construction. Columns 5 and 6 display the minimum and maximum values of the safety characteristics of the most critical elements. Column 7 shows data on changes in the mass of the coating construction when the stiffness is reassigned.

Of course, the given example of calculating reliability indicators and preventing the tendency to progressive collapse of a slab of rods is rather crude. But the methodology is applicable not only for coatings. It can be used for any rod spatial construction. Including for the entire load-bearing frame of a building or structure, which may consist of a very large number of elements. The developed program can solve such difficult tasks. This distinguishes the proposed method of ensuring the required level of reliability of the construction from other previously proposed design methods taking into account reliability requirements [40-44].

As a result of the application of the proposed design methodology, the tendency of the structure to progressive collapse has significantly decreased. The structural elements, the destruction of which can provoke a progressive collapse of the system, are reasonably determined. Design reliability indicators are determined. The safety characteristic is chosen as a reliability criterion. At the stages of iterative calculation, it took the values: β1=-1.54; β2=0.51; β3=2.67. Consequently, the overall reliability of the construction has increased. In [14] it is noted that the safety characteristic is used to calculate and justify the values of reliability coefficients. The normative levels of this value are not given, but [15] provides a reasonable gradation of β by construction reliability classes. The normative value is β = 4.3 with a reliability class RC3 (construction of increased responsibility) with a base period of 50 years. At the same time, the weight of the construction increased by 22.5%, from 6.14 tons to 7.52 tons.

• 4    Conclusions

• 1.    The approach proposed in the article makes it possible to determine with acceptable practical accuracy the reliability indicators of the analyzed statically indeterminate system of rods. This is especially true for unique large-span structures, which are high-responsibility structures, for which it is important to ensure the required level of reliability in a calculated way.

• 2.    The article considers in detail the method of reasonable selection of the most critical elements of statically indeterminate rod metal structures. The reliability of the group of the most critical structural elements of the rods will determine the reliability of the entire system as a whole. The destruction of these rods is most likely to lead to the possible occurrence of progressive collapse of the construction. The use of this methodology makes it possible to reasonably determine the most dangerous construction elements, in contrast to the methods given in the regulatory literature, which are limited to a number of generalized guidelines for the selection of the most dangerous elements.

• 3.    A software package has been developed in the MATLAB programming language. It allows you to calculate the reliability characteristics (probability of failure and safety characteristics) of spatial structures made of rods with a significant number of elements. Unlike previous works of this type, the design scheme of the construction does not need to be simplified or divided into parts and to determine the reliability characteristics piecemeal.

• 4.    Using the developed software package, the calculation of the reliability indicators of the structural coating on a square plan with a rigid support along the perimeter through the upper belt was performed. The optimization of the construction according to the reliability parameter was carried out. The methodology used made it possible to reasonably improve the strength of individual well-defined construction elements. The values of the system's security characteristics have increased to an acceptable level. The tendency of the construction to progressive collapse has significantly decreased.

• 5.    The algorithms developed in the future are supposed to develop in the following directions:

• -    justifications of calculation situations for the formation of analyzed calculation schemes;

• -    substantiation of the necessary degree of detail of the calculation schemes, which influence clarification of the calculation indicators of the strained and deformable state of the structure, and consequently, indicators of reliability of the system elements;

• -    providing the design of node connections in reliability models.

• 5    Fundings

  The research was carried out at the expense of funds provided by the Russian Science Foundation as part of the work on the project "Scientific substantiation of new approaches to the design of optimal spatial metal structures of a high level of responsibility" (project number 22-29-00139).