О барической фрагментации железа и природе текучести внешнего ядра Земли

Известно, что строение Земли имеет неоднородный характер. Согласно модели Земли Р. Хаддона и К. Буллена на глубине 2900 км (раздел Гутенберга) наблюдается резкое увеличение плотности, рост электропроводности с одновременным падением скорости сейсмических волн и вязкости вещества. Данные эффекты (в особенности исчезновение поперечной составляющей скорости сейсмических волн) привели к заключению, что внешнее ядро Земли (находящееся на глубине от 2900 до 5000 км) находится в жидком состоянии [3, 10]. При этом внутреннее ядро Земли, состоящее из тех же веществ (в основном это железо и никель), оказывается в твердом состоянии. Возникает вопрос: почему ядро, плавающее в расплаве тех же металлов, из которых оно состоит, остается в твердой фазе?

Известно также, что возникновение геотермального тепла нельзя в полной мере объяснить только лишь распадом радиоактивных изотопов калия, урана, тория и др. [12, 4]. Поэтому вопрос о возникновении тепла Земли также остается открытым. Исходя из результатов, полученных нами в работах [5—8], можно предположить, что одним из источников геотермального тепла является процесс экзотермического диспергирования кристаллов под давлением. Этим же барическим диспергированием вещества можно объяснить и наблюдающиеся на разделе Гутенберга эффекты (резкое увеличение плотности с одновременным падением скорости сейсмических волн и вязкости вещества). Обоснованию этой гипотезы и посвящена данная работа.

О методике и результатах расчетов для железа

Используемые ныне различные критерии разрушения вещества и формирования поверхностей раздела при сжатии либо растяжении кристалла содержат в своем формализме такие параметры, как удельная (на еди ницу площади) поверхностная энергия (о) и коэффициент самодиффузии (Df). Причем если функцию s используют при прогнозе условий образования трещины, то функцию Df — для изучения кинетики развития трещины при различных давлениях (P) и температурах (T). Очевидно, что функции s и П/зависят от P-T-аргументов, однако в большинстве случаев используют значения функций о и Df, полученные при невысоких температурах и при P = 0. Это связано с тем, что экспериментальных данных для о и Df при высоких P-T-условиях нет, а теоретические прогнозы используют в своем формализме различные подгоночные параметры, поведение которых в таких случаях трудно предсказать. Поэтому нами разработана аналитическая методика, описывающая с единых позиций зависимость функций о и Df как от температуры, так и от V/ V0 — относительного объема кристалла. Под «едиными позициями» здесь подразумевается, что в формализм модели не входят никакие под- гоночные константы, кроме параметров межатомного потенциала, массы атома и структуры кристалла. Здесь V/ V0 — отношение объемов при P и T, и при P = 0 и T = 0 K.

Разработанная нами методика подробно описана в работах [5, 7, 8]. Как показано [5], данный метод позволяет хорошо описать функции о( V/ V₀ , T) и D f ( V/ V₀ , T) как при изотермическом сжатии, так и при растяжении кристалла, как при высоких температурах, так и при T = 0 K. Поэтому мы использовали эту методику для расчетов свойств железа при P-T -параметрах, присущих ядру Земли.

Представим парное межатомное взаимодействие в виде потенциала Ми-Леннард-Джонса, имеющего вид [5, гл. 3]:

(1),

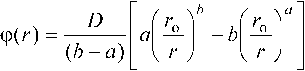
где D и r o — глубина и координата минимума потенциала, b и a — параметры: b >  a > 1.

Для проведения расчетов возьмем железо ( m = 55.847 а. е. м.) с объемно-центрированной кубической (ОЦК) структурой. ОЦК-струк-тура выбрана потому, что при высоких P-T -условияхжелезо переходит в в-фазу, структура которой рыхлее, чем гранецентрированная кубическая (ГЦК) структура Y-фазы или гексагональная плотно упакованная (ГПУ) структура Е-фазы. Параметры тройной точки между этими фазами (у-Е-в), согласно работе [13], равны: P = = 37 ГПа = 370 кбар и T = 1550 K.

Параметры парного межатомного потенциала Ми-Леннард-Джонса (1) для железа, определенные самосогласованным методом в [5], равны: r _o = 2.4775-10 ^-10 м,

D / k B = 12576.7 K,      (2)

a = 3.58, b = 8.26.

Тогда значение нормального объема для нашей модели кристалла будет равно: V 0 = N (п/6 k p ) r _o ³ = = 7.0494 см ³ /моль, где k p — коэффициент упаковки структуры, который для ОЦК-решетки равен: k p = 0.6802.

В таблице 1 представлены результаты расчетов при V/V0 = 1 (т.е. при P = 0) для фv — вероятности образования вакансии в решетке кристалла, Df — коэффициента самодиффузии (в см2/с) и о — удельной поверхностной энергии (в 10-3 Дж/м2) грани (100) ОЦК-Fe. Расчеты выполнены для температур 300 и 3000 K. Оценки других авторов при P=0 и температурах, близких к плавлению железа (Tm = 1810 K), равны [5]:

• —    1g(ф v ) = 2.43-3,

• —    lg( D f /[см ² /с]) = 7.1^8.7, о(100) = 1720-2480 [10 ^-3 Дж/м ² ].

Как видно, согласие рассчитанных значений с экспериментальными вполне хорошее.

На рис. 1 показаны изотермические зависимости функции о(100) от аргумента V/ V 0 вдоль изотерм 300 и 3000 K. Вертикаль показывает область экспериментальных данных для о(100) при P = 0. Функция о( V/ V 0 ) достигает максимума при небольших сжатиях ( V/ V 0 ) max , после чего резко уменьшается, переходя при ( V/V 0 ) fr в область отрицательных значений. На рис. 1 видно, что с ростом температуры условие фрагментации (о < 0) достигается при меньших степенях сжатия.

При сжатиях в области V / V 0 < ( V / V ) ) fr кристаллу энергетически вы

Òàáëèöà 1

Результаты расчетов вероятности образования вакансии в решетке, D f — коэффициента самодиффузии и удельной поверхностной энергии грани (100) ОЦК-Fe при V/V 0 = 1 (т.е. при P = 0)

Results of calculations of probability of vacancy creation into lattice, D f is the self-diffusion coefficient and the specific surface energy of (100) face for BCC-Fe at VIV 0 = 1 (i.e. at P = 0)

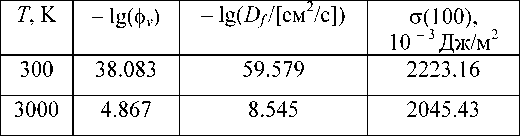
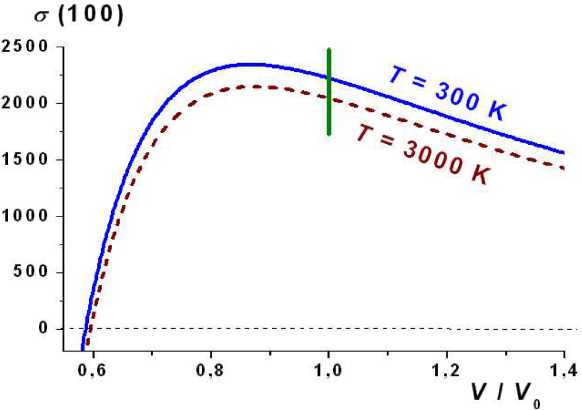
Рис. 1. Изотермические зависимости о( V / V ₀) вдоль двух изотерм: 300 K — сплошная линия, 3000 K — пунктир. Вертикаль показывает область разброса экспериментальных данных для о при P = 0. Размерность о — 10^-3 Дж/м²

Fig. 1. Isothermal dependences о( V / V 0 ) along two isotherms: 300 K — continuous line, 3000 K — dotted line. A vertical line shows the area of variation of experimental data for о at P = 0. A unit of measure for о is 10^-3 J/m²

годно любым путем увеличить свою удельную (на атом) поверхность, либо свободную, либо межкристаллитную, ибо здесь о < 0. Флуктуаци-онно отделившийся от кристалла и образовавший поверхность (свободную или межкристаллитную) домен в таких условиях будет испытывать дополнительное «поверхностное» давление [5, 7], которое тем больше, чем меньше размер домена. Это «поверхностное» давление еще более сожмет флуктуационно отделившийся домен, что приведёт к самосжатию образующихся при фрагментации доменов и к освобождению некоторого пространства между ними. Образующееся при этом «дисперсное» состояние вещества будет текучим, подобно жидкой фазе: оно примет форму сосуда, в котором находится. Вязкость «дисперсного» состояния будет тем меньше, чем больше сжимающее давление и чем меньше размер доменов.

Table 1

Таким образом, при VIV 0 < ( V/ V 0 ) fr реализуется экзотермический процесс фрагментации кристалла, который приводит к росту плотности образующихся доменов, к уменьшению вязкости образующейся «дисперсной» среды и к генерации тепла. Размерная зависимость функции о, размерное сжатие и барическая теплоге-нерация для ОЦК-Fe были изучены нами в работе [7].

В таблице 2 представлены координаты точки максимума: ( V/ V₀ ) max и ( V । V 0 ) fr — точки фрагментации, где о = 0 на изотермах зависимости о( V/V ₀) из рис. 1. В табл. 2 указаны также соответствующие данным точкам давления, рассчитанные по экспериментальной зависимости для «холодной» (упругой) составляющей давления, взятые из обзора [13]: P x = = Р₀ C ₀ ² [( V । V ₀) ^- n — 1] / n . Здесь для различных фаз железа использованы следующие параметры:

для ГПУ-e-Fe (полученные до 2.5 Мбар): р₀ = 8.3 г/см ³ , C ₀ = 4.444 км/с, n = 4.88, для ГЦК-Y-Fe (полученные до 0.4 Мбар): р₀ = 7.98 г/см ³ , C ₀ = 4.57 км/с, n = 4.0.

Для ОЦК-Fe мы использовали зависимости P(V/ V 0 , T) , полученные в работе [13] методом молекулярной динамики для T = 0 и 3000 K (табл. 2 из [2]).

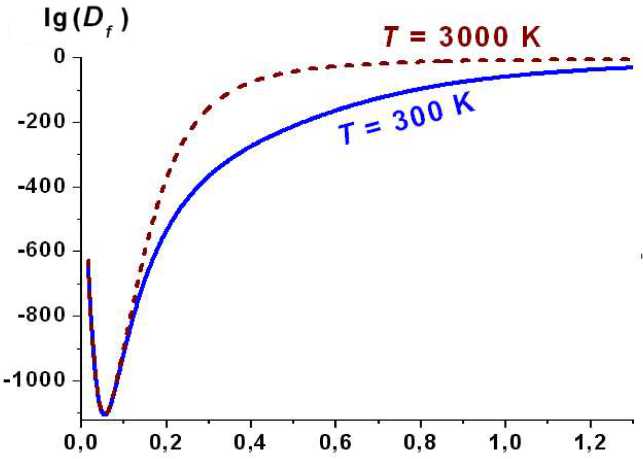
На рис. 2 показана зависимость lg( D f ) от V / V 0 вдоль изотерм 300 и 3000 K. Как видно, при сжатии коэффициент самодиффузии уменьшается, причем при V/ V₀ ^ 0.1 зависимость от температуры исчезает. Это объясняется квантовыми эффектами: при V/V 0 ^ 0.1 межатомное расстояние становится сравнимым с амплитудой колебаний атомов, что приводит к туннельному переносу атомов по объему кристалла.

При фрагментации возрастает роль межкристаллитной самодиффузии. Поэтому результаты для изотерм Df( V/ V0) из рис. 2 справедливы только при V/ V0 > (V/ V0)fr. Отклонение из меренной при V/ V0 < (V/ V0)fr изотермической зависимости Df( V/ V0) от полученной здесь зависимости для железа можно использовать для индикации барической фрагментации и для оценки роли межкристаллитной самодиффузии по «дисперсной» текучей среде.

Обсуждение результатов

Исходя из эффекта барической фрагментации (т.е. о < 0) нами была выдвинута гипотеза, согласно которой наблюдающиеся на границе нижней мантии и верхнего ядра Земли (D"-слой на глубине от 2700 до 2900 км, где P > 1.4 Мбар и T > 3500 K) эффекты (резкое увеличение плотности, рост электропроводности с одновременным падением скорости сейсмических волн и вязкости вещества) можно объяснить переходом вещества в «дисперсное» текучее состояние при высоких P-T -условиях [5, 7]. Именно

V/ V о

Рис. 2. Изотермические зависимости функции lg( D f /[см²/с]) от аргумента V / V₀ вдоль изотерм 300 K (сплошная линия) и 3000 K (пунктир)

Fig. 2. Isothermal dependences of function oflg( D f /[cm²/s]) on argument V / V₀ along isotherms 300 K (continuous line) and 3000 K (dotted line)

барическим диспергированием вещества можно объяснить как жидкоподобное поведение вещества во внешнем ядре Земли (на глубине от 2890 до 5150 км, где 1.33 <  P < 3.3 Мбар и 3500 <  T < 6300 K), так и природу геотермального тепла (которое нельзя объяснить только лишь распадом радиоактивных изотопов K, U, Th и др.). Как видно из табл. 2, значения P-T -параметров для реализации барической экзотермической фрагментации вполне достижимы во внешнем ядре Земли, которое содержит не менее 94 % Fe.

Отметим, что на «неустойчивость» кристалла железа при высоких давлениях было указано также в работе [15]. Но вместо межатомного потенциала Ми-Леннард-Джонса (1) там использовали межатомный потенциал Ридберга. Для давлений, присущих ядру Земли, и при T = 0 K в [15] была оценена величина относитель-

Òàáëèöà 2

Координаты точки максимума ( V/ V 0 ) max и точки фрагментации ( V/ V 0 ) fr на изотермах зависимости о( V/ V 0 ) из рис. 1 и соответствующие им давления

Table 2

Coordinates of the point of maximum ( V/ V 0 ) max and the point of fragmentation ( V / V 0 ) fr on the isotherms of dependence о( V/ V 0 ) from fig. 1 and corresponding pressures

T к	mm	^max 10"3Дж/м2	Рг [13] кбар	Л [13] кбар	Ре Р] кбар	(171%	Л/Д 13] Мбар	Л/г [13] Мбар	Ре/г [2] Мбар
300	0.866	2343.54	341.9	324.1	262.5	0.587	4.18	3.09	2.85
3000	0.874	2150.11	312.2	297.4	393.2	0.595	3.89	2.91	2.87

ного объема железа, начиная с которой кристалл становится «неустойчивым»: ( V/ P q ) J 0.576. Это достаточно близко к величинам, полученным нами.

Учитывая, что внутреннее ядро Земли вращается быстрее, чем мантия [3,10], можно полагать, что вещество внешнего ядра испытывает за счет этого дополнительное динамическое давление, перемалывающее вещество в мелкодисперсное состояние. Такое перемалывание должно сопровождаться экзотермическим эффектом, т. е. выделением геотермального тепла. Оценки тепла, выделяющегося при барической фрагментации железа при различных Р - T -условиях, сделаны нами в работе [7].

Но почему же в рамках данной модели барической фрагментации остается твердым (т. е. нетекучим) внутреннее ядро Земли? Ответ на этот вопрос кроется в динамике движения внутреннего ядра. И в первую очередь речь здесь идет о смещении внутреннего ядра как целого под действием приливных сил Луны. По оценкам различных авторов [1, 14], это смещение может достигать нескольких сотен метров. Легко понять, что данное смещение сопровождается сжатием вещества вдоль вектора силы притяжения и соответствующим растяжением вещества в противоположном (от центра Земли) направлении. Это сжатие, как было показано выше, должно приводить к фрагментации вещества и переходу его в текучее нанодиспер-сное состояние. Но при растяжении сжатого вещества оно опять переходит в твердое монолитное состояние. Именно эта смена сжатия вещества на его растяжение (из-за действия на вещество в центре ядра приливных сил) и приводит к существованию в центре Земли твердого внутреннего ядра. Это происходит из-за наличия в центре Земли области давлений, где P <  P fr и стабильно «монолитное» состояние, которое «плавает» в нанодис-персной текучей фазе. При этом на полюсах, через которые проходит ось вращения «монолитного», а потому и твердого внутреннего ядра, толщина внешнего жидкого ядра должна быть меньше. Вдоль оси вращения твердого внутреннего ядра давление должно быть минимальным.

Перед вулканологами давно стоит вопрос: почему «проснувшийся» вулкан, выбросив при огромном давлении и температуре определенную дозу вещества, снова «успокаивает- ся»? Ведь по физическим законам, если мантия и кора раскалываются до «расплава» внешнего ядра, где вещество находится под огромным давлением, то через этот вулкан должен вылететь весь «расплав» внешнего ядра, до выравнивания давления в ядре до атмосферного. Почему же вулкан «закрывается», выбросив определенную дозу вещества? С точки зрения предложенной нанодисперсной модели текучего внешнего ядра можно ответить следующее. Полученное барической фрагментацией «дисперсное» состояние (стабильное при P> Pr), вырвавшись на поверхность (где P < Pf.), будет метастабильным. Поэтому при P < P. «дисперсное» состояние переходит в «монолитное» с выделением энергии. При этом «монолитное» состояние будет «закупоривать» все трещины, куда проникла текучая дисперсная фаза. Выбросив определенную дозу расплава и снизив таким образом давление до P < Pfr, вулкан «закупорится» веществом в «монолитном» состоянии. Так как внутреннее давление минимально вдоль оси вращения твердого внутреннего ядра, то вулканическая активность и генерируемый тепловой поток на полюсах будут минимальны.

Вопрос о структуре ядра Земли до сих пор не решен [9]. Более того, все существующие модели ядра не могут ответить на основополагающие вопросы: почему внутреннее ядро твердое, в то время как менее нагретое внешнее ядро «жидкое»? Почему плотность внешнего жидкого ядра на 10 % ниже по сравнению с плотностью расплава железа [11]? Предложенная нанодисперсная модель внешнего ядра в состоянии ответить как на поставленные вопросы о структуре и свойствах ядра, так и на вопрос о генерации теплового потока из недр Земли.

Выводы

• 1.    Показано, что при высоких Р - T -условиях должен наблюдаться экзотермический процесс диспергирования кристалла, который, с одной стороны, приводит к резкому росту плотности образующихся нанокристаллов, а с другой — к резкому уменьшению вязкости образовавшейся диспергированной среды.

• 2.    Оценены значения объема железа, необходимые для реализации экзотермической барической фрагментации: ( V/р ) fr = 0.6 — 0.59. Показано, что они вполне реальны для ус

  ловий на разделе Гутенберга: P = 135— 150 ГПа и Т = 4000 K.

• 3.    Наблюдающиеся на разделе Гутенберга эффекты (резкое увеличение плотности, рост электропроводности с одновременным падением скорости сейсмических волн и вязкости вещества) можно объяснить переходом макрокристаллического вещества в дисперсное нанокристалличес-кое состояние под влиянием сильного всестороннего давления и высокой температуры.

Автор выражает благодарность К. Н. Магомедову, 3. М. Сурхаевой и М. М. Гаджиевой за плодотворные дискуссии и всестороннюю помощь в работе.

Работа выполнена при поддержке программы Президиума РАН (проект № 13П).