О динамическом деформировании вязкоупругой двухкомпонентной среды
Автор: Поленов В.С., Кукарских Л.А., Логойда С.М.
Журнал: Вестник Воронежского государственного университета инженерных технологий @vestnik-vsuet
Рубрика: Информационные технологии, моделирование и управление
Статья в выпуске: 3 (65), 2015 года.
Бесплатный доступ
В статье рассматривается гармоническое деформирование двухкомпонентной среды, одна компонента которой представляет собой вязкоупругую среду, наследственные свойства которой описываются ядром последействия Абеля интегро-дифференциальных соотношений Больцмана-Вольтера, а вторая - сжимаемую жидкость. Рассматривается одномерный случай. Используются уравнения движения двухкомпонентной среды в перемещениях. Решение системы этих уравнений ищется в виде затухающих волн. Вводятся безразмерные коэффициенты. Система уравнений приводится к однородной системе с комплексными коэффициентами относительно амплитуды волн в вязкоупругой компоненте и в жидкости. В результате раскрытия определителя системы получается биквадратное уравнение. Упругий оператор выражается через ядро последействия Абеля для пространства Фурье. С помощью ряда преобразований и обозначений биквадратное уравнение сводится к квадратному уравнению. Делается вывод, что в двухкомпонентной вязкоупругой среде существует два типа звуковых волн. В результате решения квадратного уравнения находятся характеристики распространения звуковых волн в вязкоупругой двухкомпонентной среде, физико-механические свойства которой представлены комплексными параметрами. Получены формулы для определения скорости распространения звуковых волн, коэффициента затухания, тангенса угла механических потерь, зависящие от свойств пористой среды и круговой частоты. Построены графики зависимостей характеристик распространения звуковых волн от логарифма температуры и от параметра дробности g.
Вязкоупругая среда, упругий оператор, затухающая волна, ядро последействия
Короткий адрес: https://sciup.org/14040495
IDR: 14040495 | УДК: 539.3;534.1
Текст научной статьи О динамическом деформировании вязкоупругой двухкомпонентной среды
Распространению упругих волн в двухкомпонентных средах посвящены работы [1-3], в которых изучаются стационарные и нестационарные волны.
Систему уравнений движения двухкомпонентной среды в перемещениях для одномерного случая запишем в виде [1]:
г 2 —' Х"г21 -— I . г2
[712° + 6712G I a + i— I ]C1 + [y22-+
I
+ 722 G 2 1 a + i - I ] C 2 — 0
V c J
Здесь
p
7 ц —-
11 H
–
упругий оператор,
а2 и111 „а2 и(2) а2 и111 д2 и |2> p 1й+Q x— £1 ~а?"+ р12 ~
~
Q ~
H
и
~
R ~
— - оператор коэффициентов
д 2 и ( 1 ) Dd2 и ( 2 ) д 2 и ( 1 ) д 2 и ( 2 )
Q--+ R--= £2--+ Р22--V дX2 дX2 12 дt2 22 дt2
где ц - модуль сдвига; Q = (1 - m)R o , R = mR o , m - пористость, R o - модуль сжимаемости жидкости; p i2 - коэффициент динамической связи твердой компоненты и жидкости; p ii = p i -p i2 , Р 22 = p 2 - p i2 ; p ii и P 22 - плотности компонент; t - время.
Индексы в круглых скобках относятся: 1 - к вязкоупругой компоненте, 2 - к жидкости.
Запишем систему (1) в безразмерной форме:
Q и R .
Решая однородную систему (4), получим
Г - 1
биквадратное уравнение относительно I a + i — I : V c J
1 — I
~ "11722 - < ~ 12 ) G I a + i- I + ( / 11 < ~ 22 + Y 22 ~ 11 -
V c J
~ 2 1 • — I 4 zx
2 / 12 7 ^12 ) G | a + 1— I + a— — 0, (5)
a — Y 11 Y 22 - Y 122
( ~,2 ( 1 ) д2 ( 2 ) Л д2 ( 1 ) д2 ( 2 )
„ 21 д W д и ’ I д и 1 д и ’
G I 7 + I Y + Y
I 11 дx 2 12 дx 2 J дt 2 дt 2 (2)
Упругий оператор ~и выразим через
ядро последействия Абеля, который в пространстве Фурье выражается формулой (4):
( Я 2/ у(1 ) Я2/ /( 2 )^ Я2/ 7(1 ) Я2/ 7(2 )
2 д и д и д и д и
G I 7 12 - 2 + 7 22 я 2 I — Y 12 + Y 22 я,2
V д x д x ) д t д t
~ 11 ( - )— 1
1 +V P
( i —т ) Y
Здесь:
H — д + 2 Q + R , р — р 11 + 2 р 12 + р 22,
G 2 — Я/ р ,
-Q R
11 H ’ 12 H ’ 22 H ’
v p — J ^r J^ , 0 < Y ^ 1
J №
у = £ 11 у =£ 11
/ 11 , / 12
рр
у = £ 22
/ 22
£
Решение системы (2) будем искать в виде затухающих волн:
где т - время ретардации, ю - частота, J « - не-релаксированное значение податливости; J o -релаксированное значение податливости; y -параметр дробности, учитывающий структурные изменения, связанные с различными видами обработки и эксплуатации материалов. Операторы — 12 и ~22 в данной задаче равны ко
, , i — t -I a + i— I x , . i — t -I a + i— I x
и ( 1 ) — C e 1 c 1 , и ( 2 ) — C 2 e 1 c J , (3)
где C i ( i =1,2) - амплитуда волн; a - коэффициент затухания; с - скорость волны; ю - круговая частота; i - мнимая единица ( i — £-1); t - время; х - координата.
Подставим значения и (1) и и (2) в систему (2), получим:
эффициентам 7 ,2 и 7 2.
С учетом (6) уравнение (5) запишем в виде:
О 4
( Y 1 - i Y 2 ) G I a + i —I + ( Г 1 + ir 2 ) •
V c J
1 — I
• G — \ a + i — I + a— — 0
V c J
Г 1
г 2 — 21 • ^° I 1 г 2
[ У н — + о*nG I a + i — | ] C + [ уц— + V c J
d 1
+ ^ G 2 1 a + i - I ] C 2 — 0 ш
I c J (4)
— Y 11 7 22 + Y 22 d 1 2 Z 12 7 12 ,
Г 2 — Y 22 d 2
— k [ ( — r у + v „ cos sr ,
1.. • ny d2 — —Vs, sin — 2 k p 2
k = J ^
(ют^ + V cos ^Y + ^ °) -Y
- тангенс угла механических потерь
Y - = ^ 22 d 1 - ^ Y 2 = О" d 2
tg Ф 2 =
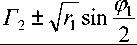
Г - ±
Для получения характеристик звуковых 2
I ю ]
волн разделим (7) на l a + z — I и введем обо- l c J
r cos 1 12
Коэффициент затухания звуковых волн можно выразить через скорость распространения волны, используя (14):
значение:
* z
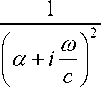
ю ф a = tg 2 (17)
с 2
где z - комплексное число.
Тогда (7) сводится к квадратному уравнению относительно z * :
аю4 z *2 + ( Г 1 + 1Г 2 G2 о ? z * + ( / - + z / 2 ) 4 = 0 (9)
Из (9) находим:
z ’ = - T G 2 ( b - + ib 2 ) (10)
2aю b, = Г, ± Л/Г cosф, b = Г ± л/Г sin ф 11 1 22 1
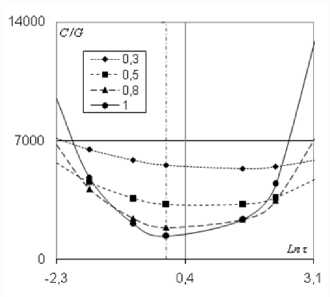
Рисунок 1. Зависимость скорости распространения звуковых волн от температуры
2 2" a п r- = V а- + а 2, ф- = arctg -2, 0 < ф- < — a2
а - = Г -2 - Г 22 - 4 ау - , а 2 = 2 ( Г - Гг - 2 aZ 2 )
Из (10) следует, что в двухкомпонентной среде существует два типа звуковых волн.
Отсюда с учетом (8) имеем:
_ . о . 2ао2 г—— а + ic " ‘\G2(b2 + b,2)ib2
ю ю 2.а I фф а + z = l sin 2 + z cos 2 I c G^ r2 l 2 2 J (12)
------ Г 2 ± T r - sin ф -
Г = a /b |2 + b22, Ф = arctg—, г- ± TT-cosф(13)
0 < Ф < n
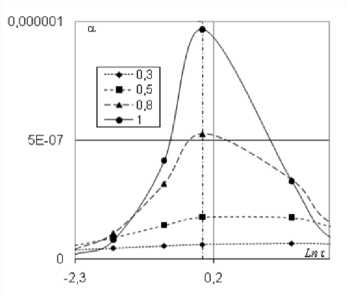
Рисунок 2. Зависимость коэффициента затухания
Равенство (12) позволяет определить характеристики звуковых волн:
- скорость с = G^H^sec фг (14)
V2 a 2 v 7
- коэффициент затухания
распространения звуковых волн от температуры
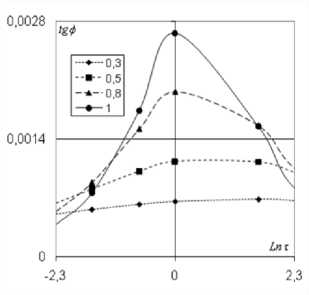
Рисунок 3. Зависимость тангенса угла механических потерь от температуры
a =
ю 2a . ф sin 2
Gr 2
На рисунках 1-3 показаны зависимости скорости, коэффициента затухания и тангенса угла механических потерь от логарифма температуры при следующих данных: J ∞ = 1, ν µ = 1, σ 12 = 0.05, σ 22 = 0.5, γ 11 = 0.9, γ 12 = -0.025,
Список литературы О динамическом деформировании вязкоупругой двухкомпонентной среды
- Био М.А. Теория распространения упругих волн в насыщенной водой пористой среде. I. Диапазон низких частот//Акуст. общество. Америка. 1956. Т. 28. № 2. С. 168-178.
- Косачевский Л.Я. О распространении упругих волн в двухкомпонентных средах//ПММ. 1959. Т. 23. Вып. 6. С. 1115-1123.
- Масликова Т.И., Поленов В.С. О распространении нестационарных упругих волн в однородных пористых средах//Известия РАН. МТТ. 2005. № 1. С. 104-108.
- Зеленев В.И., Поленов В.С. О прохождении нормально падающей поперечной звуковой волны через вязкоупругий слой//Труды НИИ математики ВГУ. 1970. Вып. 2. С. 92-100.


