О диссипации энергии в электроосмотическом процессе

ВВЕДЕНИЕ. ПОСТАНОВКА ПРОБЛЕМЫ

В работах [1–6] начат цикл статей, описывающих физические модели для реализации излучателя нового вида, основанного на использовании такого процесса электрокинетических явлений, как электроосмос. В этом цикле будут описаны физические процессы, проясняющие принцип действия этого излучателя. Одним из них является диссипативный процесс. Учет диссипации энергии в преобразователе является важным для оптимизации его конструкции.

В настоящей работе рассматриваются такие диссипативные явления, происходящие в стационарном электроосмотическом процессе, применительно к наполненному жидкостью цилиндрическому капилляру, как вязкое трение и выделение джоулева тепла. При этом ставится задача получения выражений для диссипативных членов, зависящих от всех параметров задачи.

РЕШЕНИЕ ПРОБЛЕМЫ

Диссипативная функция для случая стационарного электроосмотического течения

Согласно [7, с. 653], при движении сплошной среды (жидкости, газа, деформируемого твердого тела) диссипативная функция (ДФ) вводится для характеристики сил внутреннего трения. Она представляет собой квадратичную форму компонент тензора скоростей деформаций с коэффициентами, характеризующими вязкость среды.

В [7, с. 653] ДФ для сосредоточенных систем, по определению, равна половине полной механиче-

ской энергии, рассеивающейся в единицу времени , поэтому в настоящей работе следуем этому определению с той поправкой, что для распределенной системы ДФ равна половине механической энергии, рассеивающейся в единицу времени в единице объема . Так, для вязкой несжимаемой жидкости изменение механической энергии в объеме V определяется выражением [8, с. 79]; [9, с. 16] (здесь и далее при записи тензорных величин используется правило суммирования Эйнштейна)

d E

—

d t

- п I

V

(5 v    a v_k )

—^L + —- I d v .

(^д x k   a x )

Здесь E — кинетическая энергия в объеме V ;

( X j , x ₂, x 3 ) ^- ( x , y , z ) ; v ^- ( V j , v 2 , v 3 ) ; v — вектор скорости течения жидкости; η — динамическая вязкость жидкой среды.

Записываем (1) в виде в соответствии с соображением, приведенным выше курсивом:

—

1 d E

--- Ф d v , 2d t   V

где через Ф обозначена ДФ единицы объема. Из (1) получаем

Здесь S ik ^- 2

η

Ф - —

д v a v_k ।       ₂

⁺ I ^- nS iI .

дX, дx, J ki

Г д v    д v_k

— + —

(^д x k   ^д x

, i , k - 1,2,3 — тензор ско-

ростей деформации вязкой несжимаемой жидкости.

Согласно [10, с. 413], выражение для ε_k ² _i имеет

вид

Преобразуем член

'6k v (a x k a x

^— з ⁵ -k ^V- v I

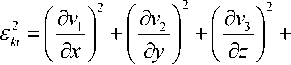
1	' d v , + d v 2	2	d v ,    d v 3 1	2	' d v 2 +d v 3'	2 1	. (3)
+-		+		+
2	ча x 2    a x i у		(d x 3    d x , у		(a x 3 a x 2 у	J

Подставляя (3) в (2), имеем для несжимаемой вязкой жидкости

Для недиагональных членов матрицы - ' ^ k имеем

' д v - + д v k (д x k д x -	i-2	fl v1 _ (д x 2	д v 2 + д x , у	2 +
	+	д v, —L + ч д x 3	2 д v 3 J д x , у	+	2 д v 2    д v 3 J +I (д x 3    д x 2 у	. (6)

Для диагональных членов г = k имеем

Ф = ns-У	= п •	f d v , J (а x J		2 +	' д v 2 J ( д У У	2 f д v3 + 1 —3 ( д z		2 I +
	1 + -	4	fl v (a x 2	+	2 vA I + д x , у		'У } ! + (д x 3	2 д v 3 | —3 I + д x , У
	+		fl v 1 (д x 3	2 + a v 3 1 д x 2 у		1 .			(4)

|А.'—2 Siv. v

₍д x_k 6x i 3

= 4

—

г

(

dv |

—1 I + дx, у

с

(

дv2 J

—2 I + дx 2 у

с

(

д v ₃ | ^д x з у

—

— 3 ( ^V- v ) 2 + 3 ( ^V- v ) 2

Именно в таком виде представлена ДФ для вязкой несжимаемой жидкости в работе [7, с. 653]. Это выражение отличается от аналогичного выражения, представленного в работе [11, с. 342] или, например, в [12], коэффициентом 1/2.

Для записи ДФ в случае однородной сжимаемой вязкой жидкости воспользуемся выражением для скорости убывания энергии такой жидкости, представленной в работе [8, с. 423, выражение (79.1)]. Диссипативная составляющая потерь выглядит там так:

= 4

v

(a x ,

r

(

d v d x.

'2 J ²

.

(

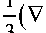
Окончательно для (5) с учетом (6), (7) имеем

Ф = n •

+

+

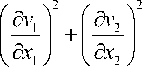
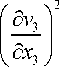
1 fdE)  = г n(дv +dvt

² l ^d t у дисс   ’ ⁴ (^д x k   ^д x -

+

—

2 Y 1    ,       2

— 35kV- v I + -^ (V- v)

d v .

Отсюда получаем для ДФ соответствующей жидкости

n д v, д vk 2 - „ Ф = - —L + — —5-k V- v

4 ( д x_k д x,   3

—

+ 2 4 ( ^V- v ) 2 .

+

'a v , +a v ,

₍d x ₂    д x ,

I + ^+dv3

I (d x₃ д x ,

I + r■

I (a x ₃ a x ₂

> +

+ ¹ ' Z — - n ] ( v - v ) ².

2(    3 JV 7

Именно в таком виде представлена ДФ в работе [7, с. 653] с той только разницей, что вместо динамической η и объемной вязкости ζ фигурируют символы µ и λ , которыми обычно обозна-

чают параметры Ламе и которые связаны с η и

Z соотношениями: n = M ; Z = ^ + т^Ц . В работе [11, с. 342] функция Ф вдвое больше.

Перепишем (8) в терминах тензора скоростей деформации [7, с. 653]:

ф = Г £2 + £2 +£?2 + 2f 82 + £2 + £2 1 + п I 611 + 622 + 633 + ^(612 + 613 + 623 )| +

1 (       2 А,       .2

⁺ 2 1 ^Z - 3 П ) ( ^V’ v ) .                  (9)

трического слоя (ДЭС) (см., например, [1]); I ₀ — модифицированная функция Бесселя первого рода нулевого порядка; r — текущий радиус капилля-

Согласно [7, с. 653], если для данной среды ДФ известна, то вязкие тензоры напряжений σ _i ^' _k вычисляются из равенств (см. выражения для σ _i ^' _k , например, в [8, с. 71])

ра.

Перепишем выражение для электроосмотической скорости в виде

v 3 ( r ) = v eo

,   I о ( r / A D )

1 0 ( a / A D )

‘ 5Ф ° k = ^" .

^{5 б} к

По определению, ДФ как функция, характеризующая рассеяние механической энергии, превращающейся в теплоту, определяет половину энергии, рассеянной в единице объема в единицу времени. Таким образом, в объеме V в единицу времени производится количество теплоты q , равное

где через v _eo обозначена электроосмотическая скорость, определяемая соотношением Гельм-гольца—Смолуховича [13, с. 159]

v

eo

εε 0 ζ _E ^η

q = 2 J ф d v .                   (10)

V

Диссипация энергии в капилляре вследствие вязкого трения

Найдем величину энергии q , выделяемую в единицу времени в цилиндрическом капилляре радиусом a и длиной l при наличии в нем электроосмотического стационарного течения. Пусть ось капилляра совпадает с осью z . Электроосмотическая скорость в цилиндрическом капилляре при приложении стационарного электрического поля E = ( 0,0, E ) , E = const имеет только одну отличную от нуля составляющую v z ( r ) = v ₃ ( r ) , определяемую выражением [13, с. 161]

Обычно при рассмотрении электроосмотического течения справедливо допущение о несжимаемости жидкости, поэтому при оценке потерь пользуемся выражением (4) для ДФ. В этом случае выражение (4) преобразуется к виду

Ф = —n

> b

V^{5 x} 1 )

(5 v 3

З д X 2

Здесь x = x , x ₂ = y , где ( x , y , z ) — декартовы координаты. Кроме того, учитываем соотношение r = 7 x ² + y ² для цилиндрических координат.

Вычисление (13) для скорости v ₃ , определяемой выражением (11), дает

1      2 1 2 ( r / A )

21     D

2 A D ⁿ eo 1 2 ( a / A D )

^v 3 ( r ) =

1 - I ° ( r / ^A D ) ££ 0 £ e

I о ( a / A D ) J 1

где v _eo определено выражением (12).

Подставляя (14) в (10), получаем количество выделяемой за единицу времени теплоты в объеме капилляра V = na ² 1 вследствие наличия вязкости

Здесь ε ₀ — электрическая постоянная; ε — относительная диэлектрическая проницаемость среды; ζ — электрокинетический потенциал;

εε k T

A D = -- —B— — длина Дебая, где c ₀ — равно-

N2(Ze) cо весная концентрация ионов1 вне двойного элек-

Q =

πl   ηv _e ² _o

A D I o ² ( a / A D )

a

J 1 12 ( ^r / ^A D ) ^{r d r} .

Вычисление (15) дает

1 ^{na 2 1} _nv 2 I ⁽ a / ^A D ) + 2 ^A D 1 ^{1 (} a / ^A D ) - 1

2 A D   ^{1 eo} [ 1 2 ( a / A D ) a I _a ( a / A D )

. (16)

¹ Здесь и далее под концентрацией ионов -го вида c принимаем отношение числа ионов N в объеме V

N к самому объему V: c =—, т.е. ci — число ионов i-го вида в единице объема.

Рассмотрим далее поведение присутствующей в (16) функции безразмерного параметра a / λ_D

I ⁽ a / ^A D ) + 2 ^A D 1 1 ⁽ a / ^A D ) - 1

1 2 ( a / A D )      a I о ( a / A D )    _ ^.

V 1 ( a / A D ) = λ_D

График этой функции, изображенный на рис. 1, позволяет предположить, что справедливо представление

^ 1 ( a / X d ) «- 0 - + b .

λD

Численная проверка в интервале значений безразмерного параметра a / λ_D на дискретном мно-

a жестве точек в интервале — е [500,3000] показы-λD

вает, что Т 1

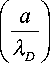
— -1 (рис. 1). Поэтому за- λ D

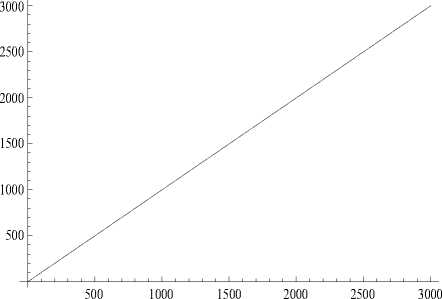
Рис. 1. График функции Т1 —

I x _d

ключаем, что b = — 1 и окончательно имеем

Т 1

a

a

( Xd

- 1.

Ось x — a / X d , ось y — ^ 1

Введем функцию невязки

А 1

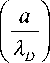
= ¥1

λ D

a

I Xd

—

На рис. 2 и 3 приведены графики функции

А 1 ( a / X _d ) в разных диапазонах.

Из рис. 2 видно, что приближение (17) становится достаточно пригодным, начиная со значения

— >  4. Поэтому выражение (16) при — >  4 λ D                                λ D

можно переписать в виде

Q =

I™,-, I ²- 1 ^{1 (} a / ^X d ) + 2 ^X D 1 ^{1 (} a / ^X d ) -1 2 ^Пео X D [ I - ( a / X d )      a 1 0 ( a / X d )

» - nv^- o ^nl

a

—

I Xd

Из этого выражения видно, что диссипация пропорциональна динамической вязкости жидкости η , квадрату электроосмотической скорости v _e²_o , длине капилляра l и величине безразмерного параметра, равного отношению радиуса капилляра к длине Дебая ^a .

λ D

Выражение (18) сразу демонстрирует различия в степени диссипации, например, для случаев, когда капилляр заполнен воздухом либо водой. Динамическая вязкость воздуха ( n _возд = 1.76 - 10 ^{— 5} Па • с) на два порядка ниже, чем у воды ( n _воды ~ » 1 ^ 10 - ³Па • с).

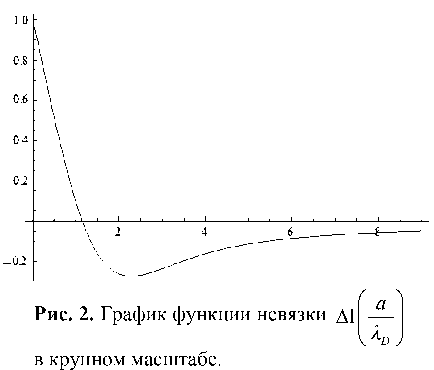
Ось x — a / X d , ось y — А1

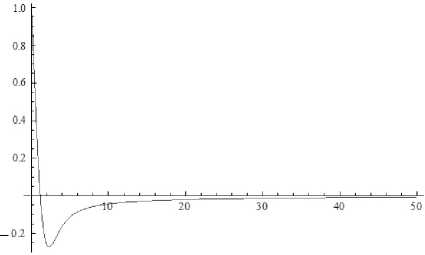
Рис. 3. График функции невязки

А 1 a в мелком масштабе.

I X d J

Ось x — a / X d , ось y — А1

Диссипация, вызванная протеканием электрического тока в жидкости

Наряду с диссипацией энергии по причине вязкого трения в электроосмотических процессах происходит рассеяние энергии вследствие наличия в жидкости электрического тока, приводящего к потерям энергии вследствие нагрева жидкости.

Прежде чем перейти собственно к потерям, вызванным выделением джоулева тепла, рассмотрим кратко такое явление, как электрохимическое перенапряжение . Перенапряжением в электрохимии называется отклонение значения электродного потенциала от равновесного при пропускании электрического тока. Величина перенапряжения зависит от плотности тока и обычно тем больше, чем больше плотность тока. При одном и том же значении плотности тока перенапряжение зависит от природы электрода и типа протекающей на его поверхности реакции, состава раствора, температуры и других факторов и может колебаться от долей мВ до нескольких В [14, с. 66].

Так в [15, с. 30] приведено соотношение, связывающее разность потенциалов AФ _e, приложенную к электродам с разностью потенциалов AФ _el, приводящую к появлению электрического тока в электролите (т.е. приложенную непосредственно на границах электролита) и перенапряжению η :

АФ _е = AO _e l + п .

Количество выделяемого в единицу времени в единице объема электролита джоулева тепла W , называемого удельной мощностью тока (УМТ) (или плотностью тепловой мощности тока ), определяется законом Джоуля—Ленца, который в линейной изотропной среде записывается так [16, § 33, 34]:²

W = j • E el .                    (19)

„   АФе|

Здесь E _el = —pl- — вектор напряженности электрического поля, приложенного к электролиту толщиной l ; j — вектор плотности тока.

Найдем мощность потерь вследствие выделения джоулева тепла W в рассмотренном выше капилляре при электроосмотическом процессе.

Выражения для искомых плотности тока в жидкости и удельной проводимости даны, например, в следующих работах по электрохимии

[13, 15, 17]. Здесь следуем [17].

Вначале определяется суммарная скорость движения ионов. Выражение для вектора суммарной скорости движения ионов i -го вида U _i под воздействием электрического поля, диффузии и движения самой жидкости имеет следующий вид [17, с. 24]:

^U. = v ei - D. — ⁺ v = ui ^E el - v D ⁺ v .     ⁽²⁰⁾

^c i                                   ⁱ

Здесь vei = uiEel — миграционная скорость иона под воздействием электрического поля Eel ; ui — подвижность иона (знак подвижности сов-x       ~ vc падает со знаком заряда иона); vD = Di—i- — i             ci скорость иона, вызванная диффузионными процессами; v — скорость самой жидкой среды.

Совокупная плотность тока j _i рассматриваемого вида ионов получается умножением в (20) совокупной скорости U _i на величину плотности заряда этих ионов p_ei = c i e i , где e i — заряд иона. Для иона i -го вида получено [17, с. 24]:³

1=0 иЕ , -eD^c + о v = i ρ ei i el i i i ρ ei

= ^Ci ^E el - ^D i ^V P ei ⁺ P ei v            ⁽²¹⁾

Для совокупной плотности тока с учетом ионов всех типов суммирование последних уравнений дает

NN

• ^j = E ^j. = E ( ^ i ^E el - D ^V P e. ⁺ P ei v ) = i =1             i =1

N

• = ^ ^E el - E ( D ^V P e- ) ⁺ P e v ,          (22)

i =1

N где pe = E pei — совокупная плотность заряда i=1

N в жидкости; ci = peiui и ст = EPeiui — парциаль-i =1

ная и полная удельная проводимости соответственно. В (21), (22) первый член справа характеризует миграционную составляющую плотности тока (ток проводимости), второй — его составляющую, вызванную диффузионными процессами, и третий член — его конвективную составляющую.

Далее, допуская наличие в жидкости только одних пар ионов одинаковой валентности, но разного знака (бинарный электролит), запишем вы- ражение (22) для плотности тока, не подразумевая выполнения условия электронейтральности, т.е. Pt + P- ^ 0 . Имеем: Pe 1 = Pt, Pe2 = P- , U = u+, u2 = u -, e1 = q, e2 = -q . Здесь q — заряд иона в единицах заряда протона. Таким образом, P+ = qc1, p- = -qc2, где c1, c2 — концентрации положительных и отрицательных ионов соответственно. Как отмечено выше, подвижность отрицательного иона является отрицательной величиной. Подставляя приведенные величины в (22), получаем

j = E ( P ei u i ^E el — ^D i ^V P i ⁺ P ei v ) =

I = 1

= ( ^PU 1 ^{- P}e |u 2 I ) ^E el ^-

- ( D , V p_e ⁺- D 2 V p - ) + ( P t + p - ) v .      (23)

Как видно, конвективная составляющая плотности тока при p e + p e Ф 0 отлична от нуля.

Вычислим удельную мощность тока W = j • E _el (19) применительно к электроосмотическому процессу в рассмотренном выше капилляре для бинарного электролита, плотность тока в котором описывается выражением (23).

Перепишем выражение (23), подставив соответствующие функции и максимально его упростив. Учтем, что р ^ , + p_e = p_e . Далее, согласно [13, с. 149],

c+ + c = 2 c 0, где c0 — равновесная концентрация каждого из ионов.

С учетом сказанного получаем следующее выражение для j :

^j = ^{2 c} 0 uq E el ⁺ P e v .

Здесь v = ( 0,0, v₃ ) , где v ₃ — электроосмотическая скорость в капилляре (11), (12).

Для УМТ W получаем:

W = j • E el = 2 c 0 uq E el ’ E el +

⁺ P e ^v • E el = ^{2 c} 0 uqE e ² l ⁺ P e v 3 ^E el ^.

Подставляя в последнюю формулу выражения (24) для ρ_e и (11) для v ₃ , окончательно получаем

W = 2 c ₀ uqE ² -

SS 0 ^Zv eo I 0 ⁽ r / ^X D )

X D    1 0 ( a / X d )

X

X

1 -

1 0 ( r / X d )

1 0 ( a / X d ) _

E .

P e ( ^r ) = ^- ss g A ^ ( r ) =

= -S ^( r ) = -λD

SsZ Io (r / X )            \ if И, (0 < r

Сравнение ДФ (14) и УМТ (25) показывает, что обе эти функции пропорциональны квадрату амплитуды вектора электрической напряженности E .

Найдем диссипирующую в единицу времени энергию q_I за счет выделения джоулева тепла во всем объеме капилляра, подставляя (25) в следующее выражение:

q , = 2 nl j Wr d r .            (26)

Вычисления дают следующий результат

Кроме того, согласно [13, с. 149, выражение (8.38)], градиенты V p_e и V p - ортогональны вектору E _el внешнего стационарного электрического поля, поэтому слагаемое D 1 V p e - D ₂ V p e в (23) на величину W влияния не оказывает (см. (19)). Далее, примем для простоты равенство подвижностей отрицательного и положительного ионов u 1 = | u ₂1 = u и учтем, что

q, =

a

= ^{2 n}l j ² c 0 uqE el

k

—

^SS 0 ^Zv eo ^E el ( 1 0 ( r / X d )

Xd    k I0 ( a / Xd )

1 0 ( r / X d )

A

p e u 1 - p_e |u ₂| = u ( c⁺q + c q ) = uq ( c ⁺ + c ) .

Тогда, согласно выражению для концентраций положительного и отрицательного ионов в приближении Дебая—Хюккеля [13, с. 148, выражение (8.33)], сумма концентраций равна4

k

1 0 ( a / X d )

r d r =

= 2 nl

a ²

2 c ₀ uqE _e ² _{l 2}

—

У

^SS 0 ^Zv eo ^E el ^X

⁴ Выражение (8.33) в [13] относится к плоской границе раздела, но имеет совершенно аналогичную структуру, что вновь приводит к равенству (24).

^a I 1 ^{( a} / ^X d ) X d I 0 ( a / X d )

1    1

2 λ D ²

—

k

f 1 1 ( a / X d ) ) k 1 0 ( a / X d ) J

Рассчитаем численно входящую в последнее выражение функцию безразмерного параметра a / λ_D :

V 2

a 1 1 ( a / X d ) X D I о ( a / X d )

1 a ²

2 λ D ²

(

V

² I

1 1 ( a / ^X d )

V i .a x , J

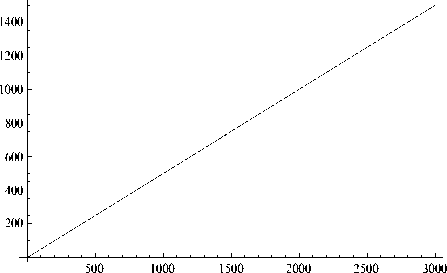
Рис. 4. График функции V2 —

V X d

График функции (28) в зависимости от аргумента a показан на рис. 4. Аналогично со случаем ДФ λD принимаем, что асимптотически при больших значениях аргумента имеет место равенство

V 2 — ^λ

f I

— — 1U v 1

2 V X d

a- I /2. V ^X D J

График функции невязки

Д 2 f V ^XD .

f

= V 2 —

V ^XD .

—

a

—

2 V X d

1 I представлен на рис. 5 (по-

сле

a _ „    .                                a

— > 4 функция невязки Д 2 — λ D

a

V Xd

■ | быстро

стремится к нулю).

Поэтому, как и в случае ДФ, величину q_I из

Ось x — a / X q , ось y — V 2

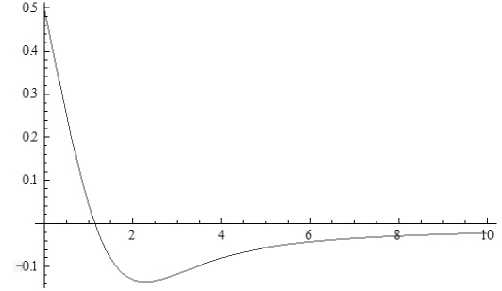
Рис. 5. График функции невязки Д2 —

V X d

(27) можно при — > 4 λD жением

аппроксимировать выра-

Ось x — a / X q , ось y — Д 2

= nl 2 c 0 uqE el a²

V

J

Окончательно имеем для суммарной мощности потерь в рассмотренном капилляре q _e = Q + q I , где Q определено выражением (18)

q e = Q + q ~ ⁿl

+

₂ ηv e ² o

V ^X D

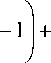
2 c ₀ uqE _e ² _l a ²

^— ее 0 ^Zv eo E el

a

A

V

V Xd

J

. (30)

Анализ выражения (30) показывает, что суммарная мощность потерь пропорциональна длине

капилляра, квадрату амплитуды вектора Eel , отношению радиуса капилляра к длине Дебая a (или иначе, величине пор). Кроме того, вели-λD чина суммарной мощности потерь qЕ линейно зависит от динамической вязкости рабочей жидкости η, дзета-потенциала ζ , подвижности ионов u , их концентрации c0 , заряда ионов q , а также диэлектрической проницаемости ε .

Баланс мощности при электроосмотическом потоке

Суммарная подводимая в электроосмотический процесс мощность равна

We =ДФei , где I — суммарный ток в электродах. В условиях,

Значения подвижности ионов и коэффициента диффузии [13, с. 145]

Характеристика	Ионы при Т = 25 °С
	H+	Ag+	K+	Li+	Na+	Br-	Cl-	F-	I-	OH-
Подвижность u иона, X10-8 м2/(в • с)	36.2	6.42	7.62	4.01	5.19	8.09	7.91	5.70	7.96	20.6
Коэффициент диффузии D , ×10–9 м2/с	9.31	1.65	1.96	1.03	1.33	2.08	2.03	1.46	2.05	5.30

когда электроосмотический процесс носит стационарный характер, что означает нулевой баланс приложенных сил, должен соблюдаться баланс подводимой к системе и теряемой в ней в единицу времени энергии. Это математически можно записать в виде W e = q _s + nI , где q _£ определяется в (30). Или в развернутом виде:

АФ eI = nI + nl

₂ ηv e ² o

T

V ^ D

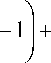
f

^{+ 2} c 0 uqE el a - ^SS 0 ^Zv eo E el

f a

\

V ^ D

Таким образом, уравнение (31) характеризует баланс подводимой в единицу времени энергии и энергии диссипации в стационарном электроосмотическом процессе.

В заключение для примера приведем в таблице значения некоторых величин [13, с. 145]. Кроме того, Z ” 100мВ [13, с. 159], ^ D » 10 нм [13, с. 150].

ВЫВОДЫ

Выше рассмотрены вопросы баланса энергии в стационарном электроосмотическом процессе в цилиндрическом капилляре, к находящейся в котором жидкости с помощью электродов приложена разность потенциалов. Рассматривается диссипация энергии за счет вязкого трения и за счет выделения джоулева тепла. Приводятся в значительной степени упрощенные выражения, позволяющие оценивать величину указанных диссипативных процессов с помощью параметров, характеризующих происходящие физические явления. Корректный учет диссипативных потерь в упоминае-

мом в работе электрокинетическом излучателе позволит оптимизировать его конструкцию.

Работа выполнена в ИАП РАН в рамках Государственного задания 075-00780-19-02 по теме № 0074-20190013 Министерства науки и высшего образования РФ.