О двойных связях на фуллеренах

Любой фуллерен C n можно представить как 3D каркас из n атомов, каждый из которых соединен тремя ребрами с соседними атомами. При этом из всех 3n/2 ребер n – одинарные, n/2 – двойные. Достоверно известно расположение двойных связей для самого стабильного фуллерена – бакибола С ₆₀ (рис. 1, a). Для второго по стабильности фуллерена С ₇₀ определены две резонансные структуры [1], которые можно объединить в одну гибридную структуру с делокализованными двойными связями (рис. 1, b). При этом ряд авторов рассматривает и другие способы распределения связей на этих двух молекулах [2; 3]. Высшие фуллерены рассматриваются в единичных случаях [4]. Но в основном их изображают без учета одинарных и двойных связей как каркасные структуры с определенной топологией.

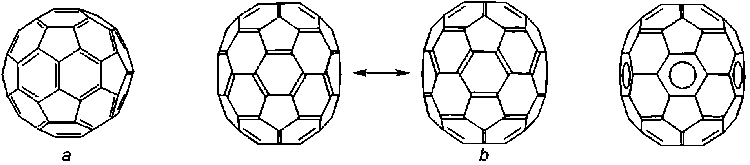
Рис. 1. Распределение двойных связей на С ₆₀ (а) и С ₇₀ (b)

В этой работе авторы моделируют распределения двойных связей на фуллеренах, основываясь на одном из принципов стабильности, постулирующем отсутствие двойных связей на ребрах пентагонов [5]. Из этого следует отсутствие на стабильных фуллеренах смежных пентагонов [6]. Подчиняющиеся этому принципу молекулы называются IPR-фуллеренами. Далее рассматриваются только они.

Теоретическая часть

Из предположения, что все двойные связи сосредоточены на гексагонах ([6,6]-ребрах), найдем их возможные типы. Всего таких типов пять (рис. 2). Их легко перечислить, располагая на гексагоне 3, 2, 1, 0 двойных связей в различных положениях и помня, что из каждой вершины должно выходить ровно 4 связи. Для каждого типа можно определить максимальное число примыкающих пентагонов. Для типа a это число равно 3, для b – 1 и для типов c, d и e – 0. Итак, лишь два типа гексагонов могут примыкать к пентагонам. Из пяти гексагонов вокруг пентагона типы а и b могут встречаться в любой последовательности и пропорции.

Рис. 2. Пять типов гексагонов. Точками показаны возможные места присоединения пентагонов

Определим классы фуллеренов, в которых все гексагоны имеют один тип. Таким типом могут быть только a или b, так как гексагоны неизбежно должны контактировать с пентагонами. Использование типа a порождает единственный фуллерен – бакибол С 60 . Тип b в одиночку на фуллерене наблюдаться не может по конструктивным соображениям (рис. 3). Таким образом, фуллерены с одним типом гексагонов представлены одним классом, состоящим из одного фуллерена – бакибола С ₆₀ с гексагонами типа a.

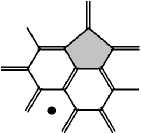
Рис. 3. Два гексагона типа b, примыкающие к пентагону, требуют для дальнейшего построения гексагон типа c (показан точкой)

Аналогично определим классы фуллеренов, в которых могут присутствовать гексагоны двух типов. Очевидно, в каждой паре должен присутствовать тип a или b. Всего таких пар 7: (a, b), (a, c), (a, d), (a, e), (b, c), (b, d) и (b, e). Не все пары реализуемы. Обозначим число гексагонов первого типа f 1 , второго – f 2 . Каждый тип привносит, соответственно, q 1 и q 2 двойных полуребер (каждое двойное ребро одновременно принадлежит двум гексагонам). Всего на фуллерене С n есть (n/2 – 10) гексагонов и n двойных полусвязей. Получим систему уравнений:

f + / 2 - n ^{- 1}0;

_ q i f l + q 2 f 2 ^- n .

Решая ее, получим выражения для f 1 и f 2 :

n 1 - q + 10q₂

fi = fl =

(     2 )     ⁴²

q i ^- q 2

n 1 - q ¹ + 10q.

• (     2 )     1'

q 2 ^- q i

Рассчитаем для каждой пары значения f ₁ и f ₂ . Числа q ₁ и q ₂ определим как числа двойных ребер на сторонах каждого типа гексагонов (рис. 2). Результаты показаны в таблице.

Таблица

Числа гексагонов для различных наборов из двух типов

Пара	q 1	q 2	f 1	f 2
(a, b)	3	2	20	n/2 – 30
(a, c)	3	2	20	n/2 – 30
(a, d)	3	1	n/4 + 5	n/4 – 15
(a, e)	3	0	n/3	n/6 – 10
(b, c)	2	2	–	–
(b, d)	2	1	n/2 + 10	–20
(b, e)	2	0	n/2	–10

Из таблицы видно, что три последних пары нереализуемы (число граней каждого типа должно быть конечным и неотрицательным). Пара (a, c) также нереализуема, т. к. гексагон типа c в данном наборе может быть смежен только с гексагонами того же типа (рис. 4).

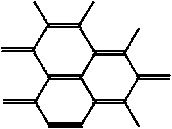
Рис. 4. Гексагон типа c в паре (a, c) может граничить только с гексагонами того же типа

Пары (a, b), (a, d) и (a, e) образуют бесконечные классы фуллеренов с определенной топологией. Пара (a, b) порождает класс фуллеренов C _{60+20 k} , пара (a, d) – класс C _{60+40 k} , где k = 1, 2, 3… (рис. 5). Для каждого k существует только один изомер фуллерена.

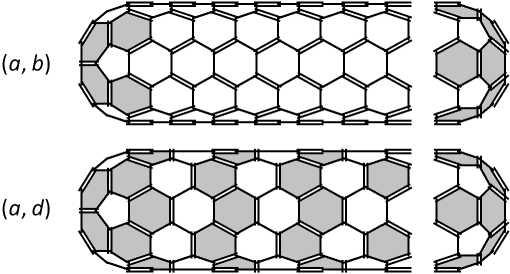
Рис. 5. Классы фуллеренов, образованные парами (a, b) и (a, d). Гексагоны типа a – светло-серые

Пара (a, e) дает большее структурное разнообразие фуллеренов посредством механизма leapfrog (рис. 6). Любой фуллерен, если перейти от него к дуальному многограннику, а затем усечь 5- и 6-валентные вершины, порождает фуллерен из класса С 60+6 k , где k = 2, 3, 4… [7]. Все усеченные грани полученного фуллерена – пентагоны или гексагоны типа e, все остальные грани – гексагоны типа a. Для некоторых k может существовать несколько изомеров фуллерена.

Рис 6. Операция leapfrog порождает фуллерен с гексагонами типа a (белое) и e (светло-серое)

Анализ наборов из трех и четырех типов гексагонов показывает, что те из них, в которых нет гексагонов типа а, нереализуемы. Для доказательства возьмем набор (b, c, d, e), который охватывает все наборы, не содержащие тип а. Рассмотрим систему уравнений

и

_< f 1 + f 2 + f 3 + f + = 2 - 10;

• 2    f + 2 f + f = 2 .

Из нее получим:

/+/4 =-10, что невозможно. Итак, на любом фуллерене (без делокализации двойных связей и их отсутствии на пентагонах) всегда присутствуют гексагоны типа а.

Не все фуллерены охвачены подобной классификацией, даже если допустить на фуллеренах гексагоны всех пяти типов. Пример – известный фуллерен С ₇₀ : распределение двойных связей на нем невозможно в рамках введенных выше ограничений. Именно поэтому для него предлагают либо проведение двойной связи по контакту пентагона с гексагоном, либо делокализацию двойных связей в гексагоне (рис. 1). Такие фуллерены можно выделить в отдельный класс, но четких критериев для этого пока не найдено.

Заключение

Отсутствие двойных связей на пентагонах приводит к пяти различным типам гексагонов. Их сочетания можно использовать для классификации фуллеренов. Гексагон типа а есть на любом фуллерене. Фуллерен с одним типом гексагона единственен – это бакибол С ₆₀ . Фуллерены с двумя типами гексагонов образуют три класса: первые два – это строго определенные классы C _{60+20 k} , образованный парой (a, b), и C _{60+40 k} , образованный парой (a, d), где k = 1, 2, 3…; третий образован парой (a, e) и состоит из типов, полученных операцией leapfrog из любого фуллерена. Запрещение двойных связей на пентагонах порождает также класс фуллеренов, которые не могут быть соотнесены ни с каким набором гексагонов.