О двухфазных акустических течениях в кавитирующей высоковязкой жидкости

The stationary cavitation jet and two-phase acoustical streaming of vortex type are formed in pure glycerin with sequential increase in the vibrational velocity up to 7 m/c and the ultrasound intencity up to 100 W/cm² at frequency 20 kHz The axled size of cavitation jet and the characteristic size of acoustical streaming more than the wavelength in the bulk Liquid.

Keyword: Power Ultrasound, high viscous Liquids, cavitation jet , two-phase acoustical streaming, foam structure.

Исследование акустических течений различных типов и масштабов обусловлено их важной ролью в механизме многих физико-химических и биофизических процессов в ультразвуковом поле [1-3].

В технологии ультразвуковой обработки вязких жидкостей широко используются стержневые излучатели при относительно больших значениях интенсивности ультразвука, обеспечивающих формирование развитой    кавитационной области [4-6]. Практический интерес представляет изучение акустических течений в условиях кавитации [5-10]. В качестве модельной жидкости для этой цели в известных работах используется глицерин, являющийся ньютоновской жидкостью с высокой сдвиговой вязкостью и прозрачностью [9-10]. В данной работе эксперименты проводились с глицерином марки «чда» с исходной вязкостью n=1,41 Pa•с.

Условия и особенности проведения эксперимента.

Эксперименты проводились при последовательном увеличении колебательной скорости и интенсивности ультразвука на частоте f = 20,3 кГц с подстройкой на частоту механического резонанса при изменении нагрузки. Для получения максимальных амплитуд смещений ξ до 100-120 мкм на холостом ходу и обеспечения длительной устойчивой работы при амплитудах ξ 50-60 мкм на нагрузку в виде кавитирующей вязкой жидкости, использовалась длинная стержневая колебательная система (рис.1). Она возбуждалась составным магнитострикционным вибратором -  4, состоявшим из последовательно соединенных магнитострикционного преобразователя, экспоненциального и ступенчатого концентраторов из титанового сплава (рис. 1,4).

Размеры кюветы - 140Х100Х30 мм. Диаметр диска излучателя d = 16мм, толщина диска h =5 мм (Рис.1). Длина волны в сплошной жидкости в докавитационном режиме - XL = 94,7 мм Соотношения hd / ^ = 0,05, радиуса диска a - a / X, = 0,08, высоты кюветы LK = 140мм - LK / Z = 1,5, величины L                  K         KL ka = 2na / XL = 0,53 .

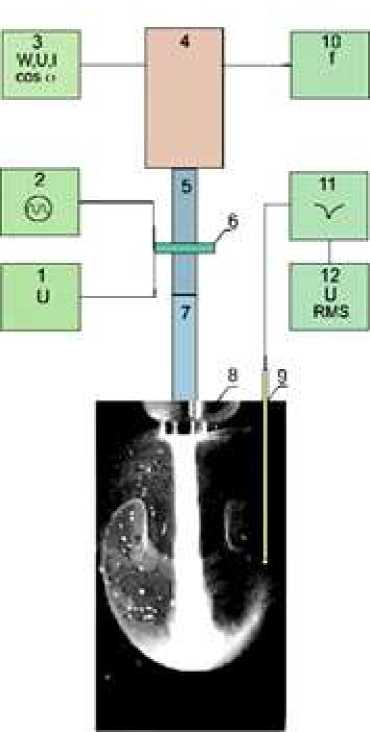
Рис.1 Блок-схема установки для изучения акустических течений в вязкой жидкости.

1-милливолльтметр, 2- осциллограф, 3-электронный ваттметр, 4- составной магнитострикционный вибратор, 5- измерительное звено, 6- бесконтактный электродинамический датчик, 7- звено излучателя с диском -8, 9-гидрофон, 10- частотомер, 11- режекторный фильтр, 12- милливольтметр со среднеквадратичным детектором (RMS).

Форма колебаний излучателя и амплитуда колебательной скорости и определялась с использованием электродинамического датчика. [12] Значения интенсивности I и сопротивления нагрузки r определялись по значениям активной электрической мощности Ne и колебательной скорости и с использованием известных методик при обеспечении работы составного магнитострикционного вибратора в линейной области. [13-14]. Падение сопротивления I ■ S излучения   Rr / Sr = рск = 2 —r-,  (рck   - волновое сопротивление

Um кавитирующей жидкости) и зависимость эффективного давления от колебательной скорости pef = ^^ рск при развитии кавитации в воде и ряде вязких жидкостей исследовалось в работах, [6,9,15-16]. В данной работе эти зависимости снималась в условиях формирования кавитационной струи при интенсивности до 100 вт/см2. Оценки давлений вне зоны излучателя и кавитационной струи производились миниатюрным гидрофоном - 10 с радиусом сферы - 1,5 мм.

Значения акустического числа Рейнольдса - Rea рассчитывались по соотношению [1]:

Rea = ^{PU m} ^ ^L , где b = 4n + Z , Z = 1,2 • П [14, 17]. 2π b            3

При изучении формирования структуры двухфазных течений использовался метод фотосъемки широкоформатной камерой в поляризованном и обычном свете при интенсивном боковом освещении. Скорость течений U (вертикальная составляющая) определялась по смещению пузырьков на границе кавитационной струи в сечении, соответствующему образованию акустического течения. По значениям скорости оценивались величина гидродинамического числа Рейнольдса Re = UL / v , где L = a^ - радиус кавитационной струи.

Результаты эксперимента.

При малых уровнях возбуждения и относительно малом значении активной составляющей импеданса - ra (ka < 2 и a / XL = 0,08) излучение жидкость мало, поскольку величина   ra = р с0   реализуется в докавитационном режиме при условии 2a > ^  [11,15-16]. С ростом амплитуды колебательной скорости и в докавитационном режиме на частоте механического резонанса активная   составляющая   r увеличивается. При этом увеличиваются интенсивность I, сопротивление излучения R эффективное давление P и давление, измеренное гидрофоном (рис.2,3a,b) .

В жидкости с исходно высоким значением вязкости росту и поступательному движению пузырька, образовавшемуся из зародыша, препятствует сила вязкого сопротивления. Известно, что при импульсно- объемном растяжении чистого глицерина в отличие от других вязких жидкостей и жидких сред диссипация энергии на начальной фазе образования пузырьков столь велика, что видимая пузырьковая кавитация практически не возникает [18]. Динамика процессов растяжения-сжатия высоковязкой жидкости в ультразвуковом поле при использовании стержневых излучателей на частотах 17-40 кГц отличается от динамики при импульсно-объемном воздействии, но влияние диссипации энергии и в этом случае столь значительно, что препятствует расширению пузырька на начальной фазе. В эксперименте это приводит к замедлению возникновения кавитации и развития кавитационного процесса при относительно высоких амплитудах колебательной скорости и и значений интенсивности I [4-6,9,22].

Спорадическое появление спектральных признаков кавитации в сигнале гидрофона и образование кавитационных пузырьков на локальных участках излучателя отмечаются при значениях величины U ² = 0,3 - 0,8 м²/с² , I = 2,7 ^ 5,7 вт/см² (рис.2). Стационарный процесс образования пузырьков и формирование кавитационной области в глицерине происходит при относительно высоких значениях величин U = 1,4 м/с , и ² = 2,1 м²/с² интенсивности I = 15,6 вт/см², давления р = 1,5 ■ 10⁵ Нм (рис.2 - линия 1, рис 3 a,b).

Диссипация энергии в высоковязкой жидкости приводит к большей, чем в воде концентрации пузырьков порядка 10⁸ - 10 9 (при радиусе R^ = 5 мкм) . Кавитация развивается в области с резко очерченными границами (рис. 4а-1). Осевой размер первоначальной кавитационной области 5 ìì . Изменение свойств жидкой среды при развитии кавитации вызывает известное явление кавитационного гистерезиса [15]. Так при пороговой амплитуде колебательной скорости и = 1,4 м/с , кавитация в глицерине сохраняется при уменьшении колебательной скорости вплоть до величины

U = 1,1 м/с . С увеличением квадрата колебательной скорости величина сопротивления излучения падает от исходного значения до относительно стабильного значения, что характерно для ряда вязких жидкостей и воды [5-6,9,15-16].

При продвижении кавитационной области вглубь жидкости формируется кавитационная струя. Рост интенсивности при этом замедляется (рис.2), но концентрация пузырьков в зоне излучателя растет, как и при развитии кавитации в воде [7]. На расстоянии 20 мм от излучателя при значениях давления р = 1,5 - 1,75 - 10⁵ H/м² (рис.2а) образуются боковые лепестки (Рис.4a-2). На рис4b показано направленное движение структуры, подобной пене. Видно, что движение участков этой структуры, отделившейся от лепестка кавитационной струи происходит без их фрагментации. Таким свойством в отличие от газо-жидкостной структуры маловязкой жидкости обладают пены.

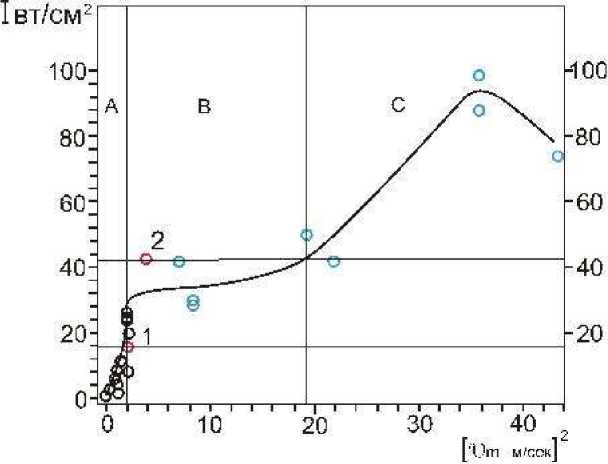
Рис 2 Зависимость интенсивности I от квадрата колебательной скорости и² 1-уроввень образования кавитационной области, 2 -уровень формирования двухфазных вихревых потоков.

Коэффициент поглощения ультразвука а в пенных структурах сложным образом зависит от кратности K = 1 + Vp / VL (где Vp и VL объем паровой и жидкой фазы соответственно), и при высоких значениях кратности (сухие пены) определяется величинами динамической вязкости, частоты, среднего диаметра пузырька d , поверхностного натяжения σ и скорости ультразвука c [23,24] :     α=ηdf 2 /σc

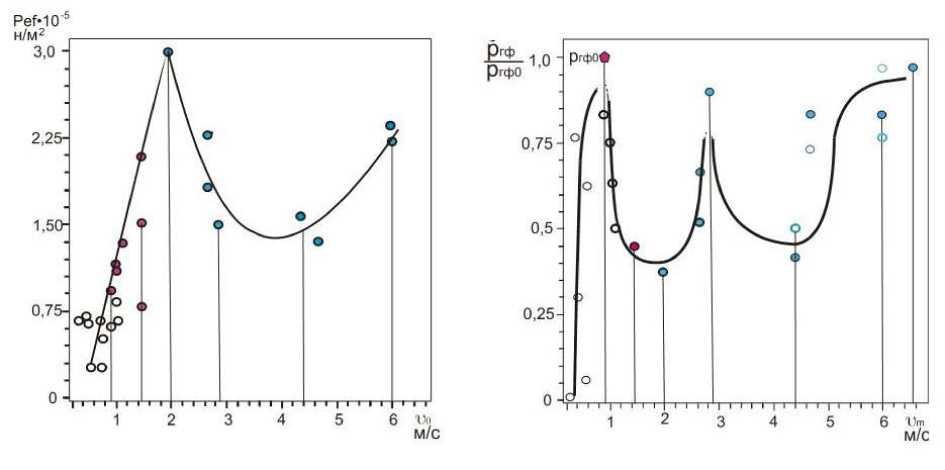
Рис 3.a,b

Зависимость эффективного давления в глицерине от амплитуды

колебательной скорости излучателя υ . a) Pef , рассчитанного по выражению (2); b)

относительного давления, определенного гидрофоном вдали от излучателя. Точки красного цвета соответствуют развитию кавитации, синего цвета формированию двухфазных течений,

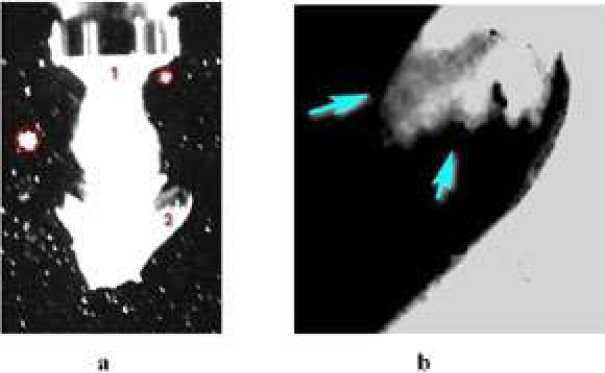
фаза формирования

Рис.4. a) - Образование в глицерине кавитационной области - 1 при значении интенсивности I =15,6 вт/см² и колебательной скорости υ = 1,4 м/с. Окружностями обозначены кластеры воздушных пузырьков. b) - начальная потока из кавитационной струи (негатив,

увеличение Х5)

соответствует области -2 на рис 2а, ( t □ 0.3 с).

Для случая вязкости η = 1,41 Pa·c , диаметра пузырьков в теле струи d=2

мкм и 10 мкм , f =20,3 кГц, σ = 5,94 ⋅ 10 ^{- 2} Í / ì , с =1923 м/c значения.

коэффициента поглощения а = 2,1 и 10,0 1/см соответственно. Вследствие этого, образование пенной структуры в условиях кавитации может увеличивать общие вязкие потери.

В поле интенсивного ультразвука пенная структура в высоковязкой жидкости образуется без введения поверхностно-активных веществ и в этом смысле не является классической пеной, но обладает таким важным свойством пен, как перемещение выделенных участков без их фрагментации, то есть с сохранением формы. Детальное изучение образования пены в глицерине выходит за рамки данной работы,

В жидкости с пузырьками, в частности в глицерине, коэффициент поглощения на порядок выше, чем в сплошной жидкости. [25]. В известной работе показано существенное отличие газожидкостной среды с пузырьками от среды с пенной структурой [26]. Параметр нелинейности для газожидкостной среды намного выше (до 40 раз), но коэффициент вязкости в пенных структурах может быть выше, чем в газожидкостной среде в 10³ раз [26].

Увеличение амплитуды скорости до и = 2,0 м/с интенсивности до значения I = 43 вт/см² (линия-2, рис.2), давления до величины Р^ = 3,1 Н/м² (первый экстремум рис.3а, второй экстремум давления на рис3Ь) приводит к росту аксиального размера струи и возникновению потоков первоначально произвольной формы. Наличие экстремумов в зависимости давления от колебательной скорости качественно соответствует аналогичным зависимостям для воды [15,16]. Но для случая высоковязкой жидкости эти экстремумы сдвинуты в сторону больших амплитуд и на порядок. При амплитуде скорости и = 2,6 м/с, некотором падении давления р = 2.3 Н/м² и интенсивности I = 42 вт/см² продолжается дальнейшее продвижение кавитационной струи вглубь жидкости.

На расстоянии 0,7 ^ от излучателя при аксиальном размере струи Lj = 66 мм (рис. 5a) и Lj = 68 мм (рис.5Ь) происходит формирование потока в виде двух вихрей (рис5а,b). Возникающие вихри могут иметь некоторую асимметрию, обусловленную асимметрией самой центральной струи (рис.5a,b). В кавитирующей жидкости скорость звука падает, и по длине сосуда укладывается большее количество волн давления, чем в сплошной жидкости, и в силу этого в ряде работ теоретически рассматривается модель акустического течения в поле плоской волны. [7].

В отличие от докавитационного режима диск излучает двумя сторонами, На рис.5с видна структура пены на границе струи -1 и на поверхности верхней части вихря -2, при этом основное тело струи остается резко очерченным. Размеры пузырьков или ячеек пены 50-150 мкм , а их размеры внутри тела струи R < 10 мкм . Вне струи и вихря видны пузырьки, радиусы которых 25 ^ 100 мкм .

На рис 6с видно, что в 50% растворе глицерина с вязкостью п = 6 -10-3 Pa-c в отличие от чистого глицерина струя распадается с образованием кавитационных тяжей, а вне струи возникают мелкомасштабные вихревые потоки (рис. 6а), последнее также отмечено для случая воды в работе [7]. Скорости потока в струе U = 0,1 - 0,12 м/с (рис 5b), хотя и меньше, чем в кавитирующей воде U = 1-3 м/с [6], U = 1,6 м/с [7], но на порядок выше, чем в чистом глицерине, в котором фронт и формирующиеся потоки имеют геометрически правильную форму (рис. 6d). При увеличении скорости с амплитуды ит = 2,6 м/с до амплитуды U = 4,4 м/с аксиальный размер кавитационной струи L возрастает до 106 мм, а масштаб акустического течения увеличивается (рис. 7 a,b). Давление падает до значения pf = 1,41 H/м. При этом происходит изменение фронта течения (рис 7 a,b) по сравнению с фронтом на рис.5а,b. Увеличение колебательной скорости до величины ит = 6,6 м/с приводит к росту размера струи до Lj □ 125 и формированию крупномасштабного

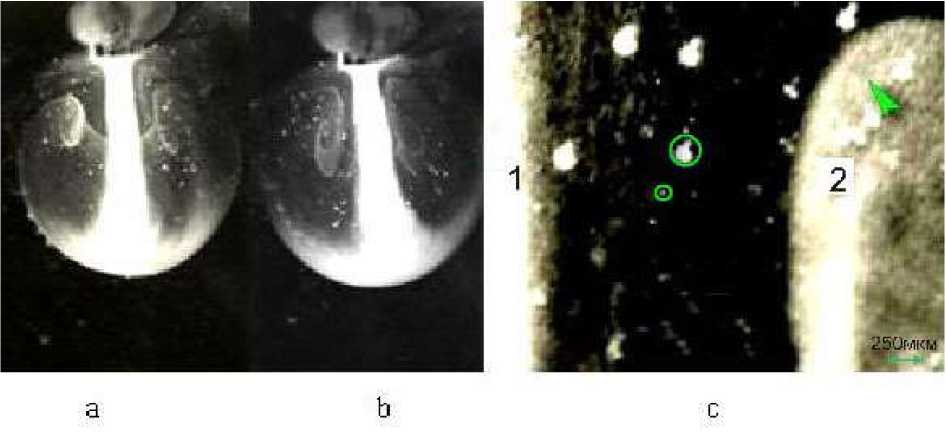
Рис. 5 a,.b - Формирование кавитационной струи, и развитие двухфазных течений при интенсивности 43 вт/см², с: 1 - кавитационная струя, 2 - верхняя часть вихря; между ними в окружностях воздушные пузырьки ( t 0, 8 с).

акустического течения размером L S > A L (рис 7 c,d,e,f). Акустические течения, формирующиеся при достижении аксиального размера струи Lj >  0,7 ^ , имеют скорости U (аксиальные составляющие) порядка 1 см/с, а соответствующие числа Рейнольдса - Re <  0,05 (рис,. 8a,b). Значения акустического числа Рейнольдса - Rea на два порядка выше. Низкие скорости течений и большой разрыв в значениях акустических и гидродинамических чисел Рейнольдса объясняется как высоким значением исходной вязкости глицерина и процессом формирования газожидкостной среды в виде пенной структуры, так и относительно малым характерного размером струи a = 5 мм (радиуса).

Рис.6. Развитие кавитационной струи в 50% водном растворе глицерина η = 6 ⋅ 10 ^{- 3} Pa∙c.

6a (2) - образование микро и мелкомасштабных потоков произвольной формы, 6b потоки на участке перед распадом кавитационной струи, 6c распад кавитационной струи ( t =0,3 c ) . Окружностями выделены мелкомасштабные потоки вне струи, 6d - Формирование двувихревого потока в глицерине с исходной вязкостью η = 1, 41 Pa·c ( t □ 0,8 c ).

Как известно, образование крупномасштабных акустических течений обусловлено всеми видами необратимых потерь, но их скорость определяется вязкими потерями [1]. Выражение для оценок характерного времени установления τ эккартовского течения приведено в работе [2]:

τ =

r ₀ρ₀

(μ₁²)² η ,

где μ ² = 5,136 - первый нуль функции Бесселя второго порядка - J ( x ) ,. r

• - радиус трубы.

Теория эккартовского течения основана на допущении, что изменение скорости течения вдоль оси трубы пренебрежимо мало, а сила F(x), остается по оси трубы постоянной [1,2].

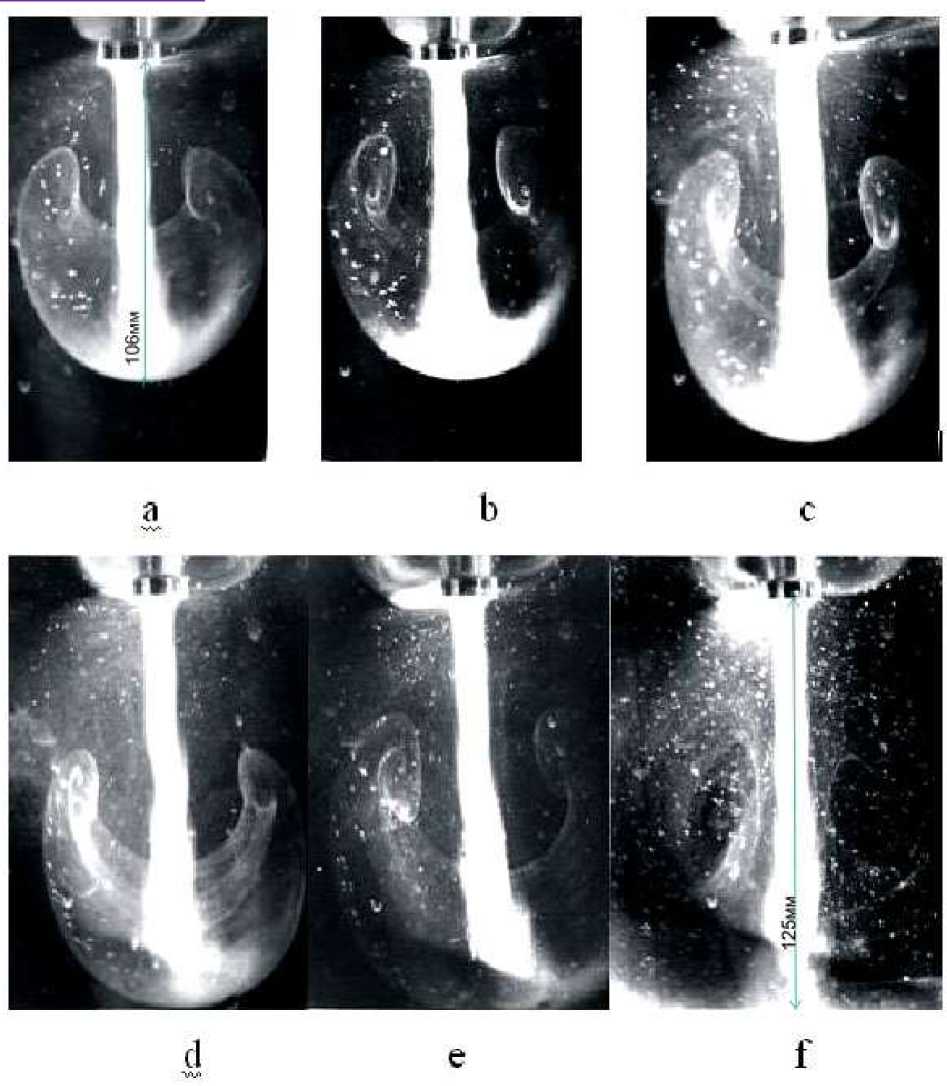
Рис 7 a-f Развитие кавитационной струи и формирование акустических течений при увеличении интенсивности: c-51 вт/см², d- 75,7, e - 90 вт/см² , f - 99,3 вт/см².

Такое допущение некорректно для вязких жидкостей и глицерина с

П = 1.41 Pa-c. Но сопоставление времени т на качественном уровне можно провести для воды и часто используемого в экспериментах 50% водного маловязкого раствора глицерина. Отношение времени установления

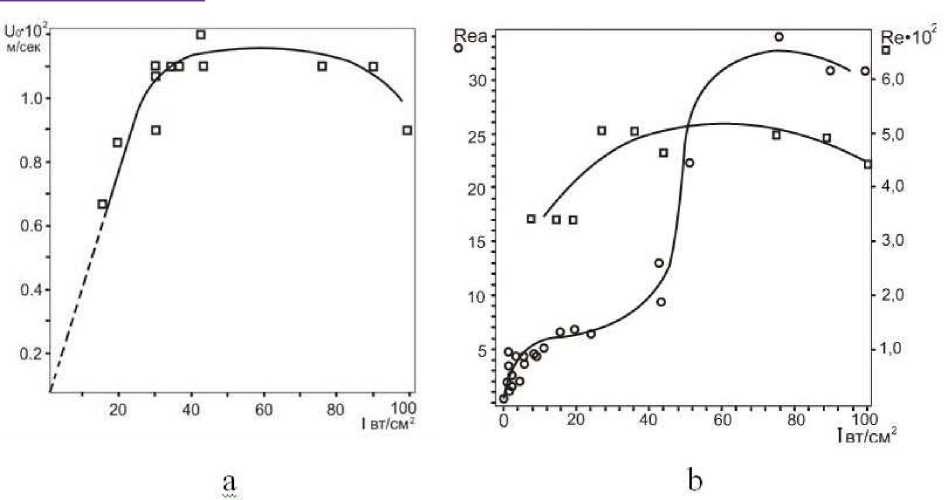
Рис. 8a,b. а -Величины скорости акустических течений, b - акустического -Rea и гидродинамического - Re чисел Рейнольдса при последовательном увеличении интенсивности ультразвука.

течения в воде к времени установления в 50% глицерине определится отношением значений их кинематических вязкостей:

τ _W / τ _G = ν _G / ν _W = 4.8      (5)

Вязкость воды η=10-3Pa⋅c, 50% глицерина  η= 6⋅10-3Pa⋅c . При радиусе трубы r = 3 см τ = 34,1 для воды, для 50% глицерина τ = 7,1 секунд.

Эккартовское течение является одномерным течением. Потоки в высоковязком глицерине имеют двувихревую структуру. Это течение в силу конфигурации и соотношения размеров кюветы на качественном уровне можно рассматривать как плоское. Теория процесса установления двухмерного течения, в жидкости с большим поглощением, известно только для течения в трубе [2]. Для двумерного плоского течения известно численное решение для функции, определяющей линии тока течения в прямоугольном сосуде [27]. Скорость такого течения зависит от величины поглощения, а также сложным образом зависит от характерного размера сосуда и поперечного размера звукового пучка [27]. Однако время установления такого течения неизвестно.

Время установления двухмерного плоского течения можно рассчитать при

UL численном решении уравнения переноса вихря для случая Re = — << 1

V

• [28] . Порядок времени установления рассматриваемого в данной работе, можно оценить как время диффузии вихря, принятого в гидродинамике для случая с малыми числами Рейнольдса [28]. При оценках на качественном уровне для случая Re <<  1 максимальное время диффузии вихря:

т = L 2 / v , UL/ V = 0.01 , т = L ²/ v = 0,01 L / U ,

Где U -скорость набегающего потока. В случае плоского течения L -характерный размер - хорда внешней линии тока вихря, ближайшей к стенке сосуда. При значениях L = 6 см, v = 11,18 стокс , т = 3,2 секунды, но величина скорости U = 0,02 см/с, что на порядок ниже экспериментальных значений.

Экспериментальные оценки времени увеличения аксиального размера кавитационной области в вязких жидкостях от момента включения ультразвука до видимых размеров составляют: в эпоксидной смоле через 2 секунды - 10 мм и через 9 секунд до 30 мм [6]. В глицерине кавитация возникала через ~ 10 секунд, а время установления потока размером 30мм составляло 3,5 секунды [9]. В предлагаемой работе увеличение аксиального размера кавитационной области до 5 мм в глицерине составляло 10-12 секунд. В связи с этим следует отметить, что возникновение крупномасштабного кавитационного течения в высоковязкой жидкости, как показано в данной работе (рис.5), возможно лишь при достижении определенного размера кавитационной струи., Таким образом, суммарное время развития кавитационной области и установления течения масштаба больше  LT > ^ может составлять нескольких десятков секунд.

Заключение

При величине колебательной скорости и = 1,4 м/с и интенсивности I = 16 вт/см² в глицерине с исходной вязкостью п = 1,41 Pa^c образуется кавитационная область, из которой при интенсивности I = 19,6 вт/см² формируется стабильная кавитационная струя. С ростом аксиального размера струи до значения 0,7 X_L при величине интенсивности I = 42 ^ 43 вт/см² возникают вихревые потоки, а при интенсивности I = 70 - 100 вт/см² - крупномасштабные течения L_s □ L_K со скоростью порядка 1 см/с .