О флексоре Штеффена

Многогранные формы окружают нас повсюду. Почти все сооружения, возведенные человеком, от древнеегипетских пирамид до современных небоскребов, имеют форму многогранников. Серьезный интерес к многогранникам возник еще в глубокой древности и проявлялся не только в рамках математики и ее приложений. Богатая и древняя история многогранников связана с именами Пифагора, Евклида, Архимеда, Аполлония. Платон и Кеплер привлекали многогранники для философского осмысления окружающего мира. Благодаря изяществу своих форм многогранники вошли в искусство (живопись, скульптура). В то же время теория многогранников - один из интереснейших разделов современной геометрии. Теория многогранников имеет большое значение как для теоретических исследований, так и для практических приложений в других разделах науки, например, алгебре, теории чисел, в естествознании, кристаллографии, в бурно развивающихся в последние десятилетия областях прикладной математики — линейном программировании, теории оптимального управления, математических методов в экономике и т.д. Вопрос - однозначно ли задается форма многогранника своими гранями или она может меняться за счет изменения двугранных углов, давно интересовал математиков. В 1776 г. великий Леонард Эйлер высказал гипотезу: «Замкнутая пространственная фигура не допускает изменений, пока не рвется». Под «замкнутой пространственной фигурой» понималось то, что сейчас принято называть замкнутой поверхностью. Тем самым предположение Эйлера относилось не только к многогранным поверхностям.

Склеивая из картона выпуклый многогранник, любой школьник заметит, что в начале работы фигура, полученная соединением в одной вершине более трех граней, может оказаться гибкой (допускающей вращение граней вокруг своих ребер, то есть изгибаемой), но в законченном виде фигура уже не будет гибкой: если нажать на нее достаточно сильно, то либо грани деформируются, либо склеенная модель многогранника порвется. Многогранник, который может непрерывно деформироваться так, что его грани остаются плоскими и равными самим себе и меняются лишь его двугранные углы, называется изгибаемым.

Если же такой непрерывной деформации не существует, то многогранник неизгибаем. В 1813 г. в «Журнале Политехнической школы» была опубликована замечательная работа «О многоугольниках и многогранниках» выдающегося французского математика Огюстена Луи Коши, в которой недавний выпускник знаменитой Политехнической школы доказал теорему о единственности выпуклого многогранника с данными гранями. Для доказательства этой теоремы Коши предложил новый метод, который, по словам академика А.Д. Александрова, «представляет собой одно из прекраснейших рассуждений, какие только знает геометрия». Теорема Коши подтвердила гипотезу Эйлера в случае выпуклых многогранников. На протяжении двух веков геометры верили, что не только выпуклый, но и невыпуклый многогранник также неизгибаем. И только совсем недавно, после 164 лет сомнений, этот вопрос был решен. В 1977 г. американский геометр Роберт Коннэлли построил примеры изгибаемых самонепересекающихся многогранников и тем самым опроверг гипотезу Эйлера. Коннэлли назвал такие многогранники флексорами. Более того, в 1996 г. российский математик И.Х, Сабитов доказал, что флексоры при изгибании сохраняют объем.

В наши дни бурное развитие получили системы компьютерной математики для персональных компьютеров, несомненным лидером среди которых является компьютерная система “Mathematica”, созданная фирмой Wolfram Research,Inc. во главе с ее президентом и главным разработчиком программ Стивеном Вольфрамом. Огромное преимущество системы Mathematica состоит в том, что множество ее операторов и способы записи алгоритмов просты и естественны. Как правило, здесь не надо особенным образом заранее объявлять тип переменных, не надо специально распределять память для хранения той или иной информации. По простоте работы Mathematica превосходит Basic. Это происходит за счет укрупнения команд, которое делает написание программ в Mathematica более коротким и удобным. Это значит, что научиться работать в системе Mathematica довольно просто.

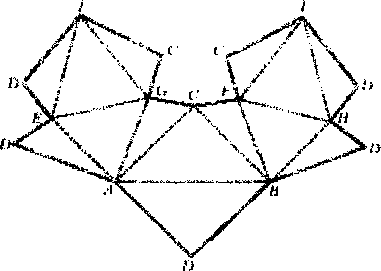
Рис. 1.

Справочная база системы вмещает в себя объем информации, эквивалентной десяткам толстых справочников и при этом отличается очень быстрым поиском нужной информации по ряду критериев, причем сопровождаются «живыми» примерами, которые можно изменять в ходе просмотра справочных данных.

Нами на языке компьютерной системы «Mathematica» написана программа, которая представляет компьютерную модель флексора с 9 вершинами, оригинал которой построен в 1979 г. геометром К. Штеффеном.

На рис. 1 показана развертка такого флексора, приведенная в работе [1]. Разный вид пунктирных линий на развертке означает, что грани перегибаются вдоль этих линий в противоположные стороны.

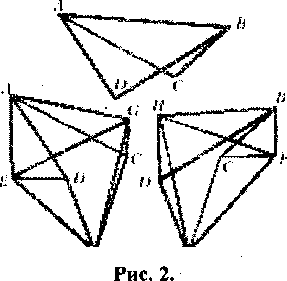
На рис. 2 показана схема сборки многогранника Штеффена.

На рис. 3 показан вид компьютерной модели флексора. А,В-конек крыши, треугольники АВО1 и АВ02-скаты.

Рис. 3.

изводит неизгладимое впечатление. Однако при их описании в статье эффект от созерцания таких картинок исчезает, поскольку анимация при этом невозможна. На рис. 4 приведен стоп-кадр анимации изгибания флексора.