О форме и условном диаметре реальных частиц зернового материала

Известно, что от формы частиц зернового или другого дискретного материала и их условного диаметра зависят расходные характеристики бункеров и особенно бункеров-дозаторов, их наибольшие сводообразующие выпускные отверстия, насыпная плотность зернового материала, углы давления и ориентации зерновок в объеме бункера и, следовательно, распределение статических и динамических нагрузок, действующих со стороны сыпучего тела на стенки и днища бункеров [1–8].

В механике сыпучих тел при теоретическом решении задач, связанных с исследованием процессов хранения, дозирования, транспортирования и истечения зернистых сыпучих материалов, определение условного диаметра дискретных реальных частиц осуществляется по известной формуле проф. Л.В. Гячева [2]

d y = V a ■ b ■ c, (1)

где a, b и c– соответственно, длина (высота), ширина и толщина реальной частицы, м.

Из формулы (1) следует, что условный диаметр частицы dyравен среднегеометрическому размеру частицы и не зависит от ее формы. Это противоречит производственному опыту и результатам экспериментальных исследований. Форма реальной частицы и ее условный диаметр оказывают влияние на протекание указанных процессов, а также на конструктивные и технологические параметры устройств их реализующих.

В природе формы реальных частиц зернистых материалов многообразны, однако, каждая из них может быть выражена одной из пространственных фигур стереометрии [9, 10]. Например, семена гороха близки по форме к шару; кукурузы – к пространственному клину или пирамиде; зерно пшеницы – к параболическому бочонку (рисунок); семена подсолнечника – к пря-

мому конусу или пирамиде и т.д.

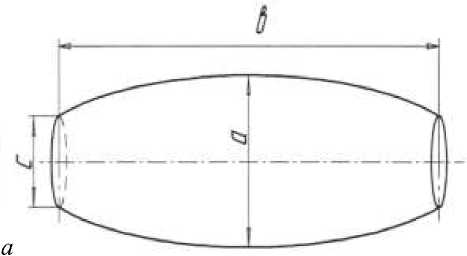
б

Натуральная форма ( а ) и схема ( б ) зерновки пшеницы

Исходя из принципов геометрического подобия, любую частицу, по форме подобную реальной, но изготовленную из пластичного материала, можно обратить в шарообразную с сохранением ее объема и массы. Отсюда следует, что для определе- ния dy реальных частиц можно их объемы из ряда пространственной стереометрии приравнивать к объему шара. В результате получим:

• -    для реальной частицы в форме шара

— = %_и   = 1,0;

6       6

- для реальной частицы в форме пря- мого цилиндра redy3    red ц 2

—— = —— а;

6       4

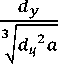
1,14;

- для реальной частицы в форме пря- мого конуса redy3

1 red_K ² --а;

3   4     ’

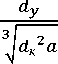
0,80;

• -    для реальной частицы в форме прямого параллелепипеда

^redy           ,           ^dy        A Л

• — = = а-Ь-с ; — = 1,24;

6                  Ча-й-с

• -    для реальной частицы в форме правильной пирамиды

^red y     ^{1          d} y      л or

• — — = -Ғ^а; зт= = 0,86;

6      3       ’  ³VF ^: a

• -    для реальной частицы в форме пространственного клина

redy- = 1a • 6 • с; 3.dy = 0,98; 6    2         ЧаҒс

• -    для реальной частицы в форме параболической бочки

  _______ ^dy _______

  ³VCsK 2 +4b-c+3c 2 )a

  
  

  0,47.

  
  

Из этих выражений следует, что для любой конкретной формы реальной частицы существует вполне определенное соотношение между ее условным диаметром и среднегеометрическим размером. Фактически это соотношение определяет форму реальной частицы и его можно назвать коэффициентом формы реальной частицы.

Таким образом, условный диаметр любой реальной частицы равен не среднегеометрическому ее размеру, а произведению коэффициента ее формы на ее среднегеометрический размер, то есть, dy = кф fсгр, (2) где кф - коэффициент формы реальной частицы;

f сг . _р — среднегеометрический размер реальной частицы, м.

Коэффициент к ф показывает, во сколько раз d y по своим размерам отличается от среднегеометрического размера реальной частицы. Как следует из указанных выражений, относительные разницы между d y и f _сг . _р по абсолютному значению составляют: для шаровидных частиц - 0%; для частиц в форме прямого цилиндра -14%; в форме прямого конуса - 20%, в форме прямого параллелепипеда - 24%; в форме правильной пирамиды - 14%; в форме пространственного клина - 2%; в форме параболической бочки - 53%.

Если реальная частица визуально по своей форме не напоминает ни одну из фигур стереометрии, то условный диаметр этой частицы можно определить исходя из формулы, выведенной для частицы в форме прямого параллелепипеда:

dy = 1,24 Va • 6 • с, (3)

при условии, что измеряемые параметры a, b и c - максимальны.

В таблице приведена структура формул для определения условного диаметра некоторых реальных частиц, по форме близких пространственным фигурам стереометрии.

В таблице приняты следующие обозначения: а - длина частицы, м; b - ширина частицы, м; c - толщина частицы, м; d_m - диаметр шаровой частицы, м; d_ц -диаметр основания цилиндрической частицы, м; d_K - диаметр основания конической частицы, м; F - площадь основания пирамидальной частицы, м².

Структура формул для определения условного диаметра некоторых реальных частиц

№ пп	Форма частицы	2 8 § « -ә	Среднегеометрический размер частицы	Условный диаметр частицы	Измеряемый параметр
		к ф	^ сг.р , м	dy , м	a, м	b, м	с, м	d ш , м	м	d к , м	F, м2
1	Параболическая бочка	0,47			+	+	+
			V(8b 2 + 4b - с + 3с 2	0,4?V(8b 2 + 4b • с + 3
2	Тетраэдр	0,61	3 70 3	0,61 а	+
3	Двуосный эллипсоид	0,73			+	+	+
			V(b + с)2a	0.73 7(b + с) 2 а
4	Прямой конус	0,80	Vd к "а	0,8 ^d к2 a	+					+
5	Правильная пирамида	0,86	Vf •а	0,86 VF • a	+						+
6	Пространственный клин	0,98	Va-b -с	0,98 Va • b • с	+	+	+
7	Шар	1,00	> ш 3	31^				+
8	Прямой цилиндр	1,14	3 Jd ц 2а	1,14 3 Jd ц2 a	+				+
9	Прямой параллелепипед	1,24	Va-b-с	1,24 Va • b • с	+	+	+
10	Куб	1,24	V0 3	1,24 Va 3	+
11	Нестандартная форма	1,24			+	+	+
			V amax - bmax "  стах	1> 24 V a max " b max "  с тах

Обобщенный анализ изложенного материала и данных таблицы позволяет сделать вывод, что условный диаметр реальной частицы следует определять не как ее среднегеометрический размер, а как произведение среднегеометрического размера на коэффициент ее формы, причем для любой реальной частицы коэффициент формы может быть определен аналитически.

В качестве исходных данных для расчета коэффициента формы частицы могут быть использованы их отдельные линейные размеры, которые легко получить путем измерений.

Проведенные расчеты для частиц различных форм показали, что данный коэффициент варьируется в значительном диапазоне – от 0,47 до 1,24, что не может не сказаться на достоверности полученных теоретически результатов.