О форме образующей стенки конического бункера наибольшего расхода

До настоящего времени отсутствует аналитическое решение по определению формы образующей стенки конического бункера наибольшего расхода зернистых материалов.

Необходимость такого решения обусловлена широким использованием конических бункеров в сельскохозяйственном производстве из-за простоты их конструкции и относительно небольших материальных затрат на их изготовление.

Как известно, в любом поперечном сечении конического бункера (рис. 1) скорость сыпучего тела, подчиняющегося закону Кулона, определяется по формуле где q - объемный расход сыпучего тела, м3/с,

S - площадь текущего поперечного сечения бункера, м².

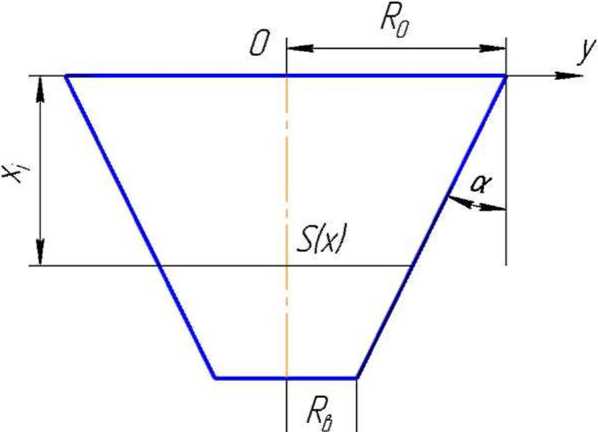
Рис. 1. К определению формы образующей стенки конического бункера наибольшего расхода:

Д. - входное отверстие бункера; Кв- выпускное отверстие бункера

Тогда ускорение сыпучего тела в лю

бом поперечном сечении бункера dv d ( q Л а- — = — —— .

di dt\S^ ;

уравнение истечения) в случае, если рассматриваемое сечение «t_z» будет служить

выпускным отверстием бункера:

Выполнив дифференцирование и положив a g, найдем соотношение между объемным расходом и объемным ускорением сыпучего тела (дифференциальное

^ = ^-ЭД + dt

[Эд)]2 *

Решение этого дифференциального

уравнения имеет вид

q = ЭД-

х0.5      /             \0,5

<гЭД) /Д ( g-swl ( S'W J " \  эд J

где th — гиперболический тангенс. Или

— =^-5(х)- Х-іһ'

эд J

Если в формуле (3) положить — = 0 или в формулах (4) и (5) устремить Г —>оо, получим предельный расход бункера при условии, что рассматриваемое сечение «х_» является выпускным отверстием бункера

У усеченного конуса площади поперечных сечений

S^ = 7T-y\          (7)

Тогда q„„ = ^-y(-^ -    (8)

Пользуясь формулами (6) и (8), можно построить кривую зависимости «q » от «т».

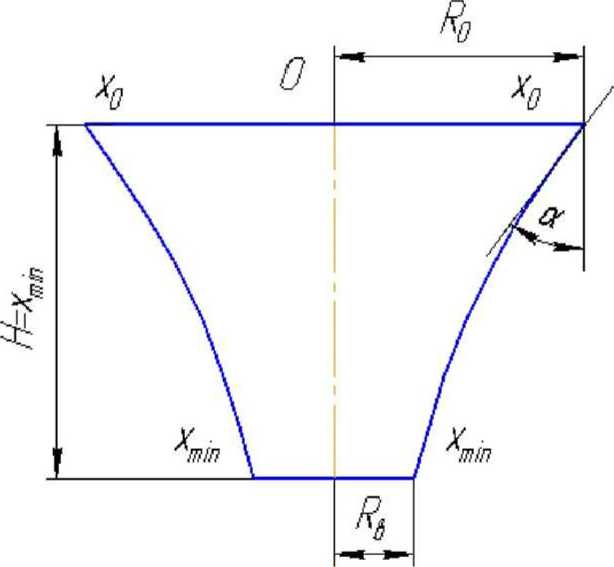
Рис. 2. Конический бункер с криволинейной образующей стенки

Истинный предельный расход бункера будет, очевидно, определяться сечением, которое имеет наименьшую пропускную способность. В случае конического бункера, который является сужающимся, таким сечением будет являться выпускное отверстие, так как оно имеет наименьшие размеры, величина же у* = -Iga = const. Зависимость qni)=.fW у таких бункеров монотонно убывает.

Для бункера с криволинейным продольным сечением (рис. 2) зависимость q ~ .fW может иметь в интервале 0 х<Н минимумы. Сечение xniin (см. рис. 2), соответствующее наименьшему минимуму функции q = f\x^, ограничивает пропускную способность (расход бункера) всего бункера. Струя сыпучего материала претерпевает в этом случае разрыв, так как при х > лгіпіп частицы дискретного сыпучего тела совершают свободное падение с ускорением «g».

Таким образом, для определения истинного расхода сыпучего дискретного материала из конического бункера с криволинейной образующей его стен достаточно найти наименьший минимум функции (4) или наименьшее значение этой функции в интервале 0<х<Н. При исследовании этого удобнее рассматривать функцию

» = ^,=/W. (9)

Для модели зернистого сыпучего тела нетрудно решить и другую важную задачу - найти форму кривой продольного сечения бункера, обеспечивающую наибольшую пропускную способность бункера. В этих случаях необходимо добиться того, чтобы максимальный расход каждого последующего (более узкого) сечения был не меньше максимального расхода каждого предыдущего сечения. В пределе расход каждого последующего сечения должен быть равен расходу предыдущего (бункер постоянной во всех сечениях пропускной способности).

Бункер, форма которого определена из указанного условия, имеет наибольшую пропускную способность среди всех таких же бункеров, имеющих заданные параметры входного отверстия, и может быть назван бункером наибольшего расхода.

Приравняв нулю производную выражения (9), получим дифференциальное уравнение, определяющее поверхность конического бункера наибольшего предельного расхода:

5(x)-S"(^) = 3[s''to]2-       (10)

Проинтегрируем уравнение (10), приняв начальное условие s^=s#, sx^=s;.

Получим следующее соотношение между площадями и абсциссами поперечных сечений бункера наибольшего расхода:

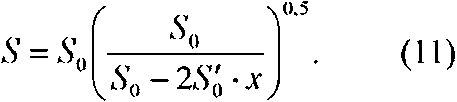
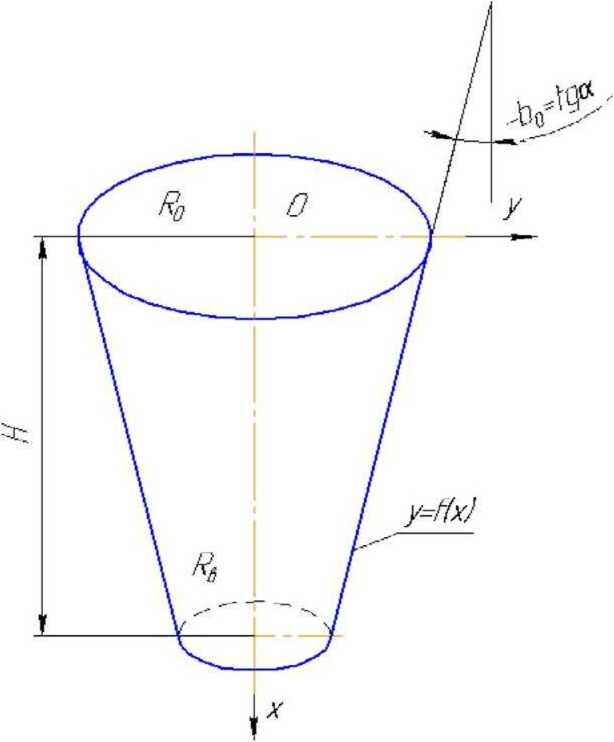
Рис. 3. Форма конического бункера наибольшего расхода

Предельный расход такого бункера, согласно формуле (6), определяется параметрами ^ и 8^ входного отверстия «7?₀»:

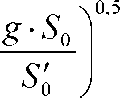
Решив формулу (12) относительно S^ и подставив значение Sq в уравнение (И), получим зависимость между 5 и г при заданном предельном расходе бункера и площади начального его сечения «Л"о -х0»

(см. рис. 2).

В частности, если положить

3/(0) = ^,)/ = -^ =/^а, т0 формулы (И),

(12) и (13) для решаемого бункера примут вид:

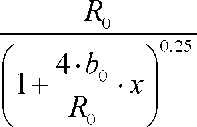
• (15)

Форма же сужающегося конического бункера наибольшего расхода будет иметь вид, показанный на рисунке 3.

Этот бункер предназначен для гидравлического истечения зернистого сыпучего материала.

Выводы

• 1.    Для конического бункера наибольшей пропускной способности форма образующей его стенки должна выполняться по квадратичной параболе.

• 2.    Предельный (максимальный) расход сыпучего зернистого тела из такого бункера повышается на 15...20%.