О формировании структур в неравновесных средах при резонансном трёхволновом взаимодействии

Формирование нелинейных структур при резонансном взаимодействии волн различной природы является предметом большого числа исследований [1 –4]. При этом многообразие эффектов и структур, формирующихся при этом взаимодействии, не до конца исследовано даже в одномерном приближении. Кроме того, в последнее время появились работы, где исследуются особенности формирования многомерных структур, в частности, спиральных структур, возникающих в цилиндрически симметричных и радиально неограниченных системах [5 –7]. Однако существующие результаты носят довольно отрывочный характер и обычно не учитывают неустойчивостей, развивающихся в активных средах.

В данной работе исследованы некоторые особенности формирования одномерных и спиральных структур в неравновесных средах, возникающих при трёхволновом резонансном взаимодействии волн вида

ω ₂ = ω ₀ + ω ₁ + ∆ω , k ₂ = k ₀ + k ₁ + ∆ k , m ₀ + m ₁ = m ₂ , (1) где ω j – частота волны, k j и m j – аксиальное и азимутальное волновые числа, ∆ω и ∆ k – расcтройки частот и волновых чисел взаимодействующих волн соответственно.

1. Основной формализм

Пусть векторное поле й в слабонелинейной среде описывается системой уравнений вида

ди -    - (- дй — _)

+ Lu = N u ,   , ∇ u ,                        (2)

д t          к д t    У где вид линейного и нелинейного операторов Lˆ и N определяется видом системы конкретной природы [1 –4].

Разыскивая решения системы (2) в виде суммы трёх волн 2

й = ^ й j B j ( e z , е t ) e i j + ' ^т ' ^ф ' ™ j ‘ + к .с .,                  (3)

j = 0

полагая выполненными условия взаимодействия (1), после стандартных преобразований приходим к систе- ме укороченных уравнений для комплексных амплитуд взаимодействующих квазигармонических волн

^∂ B 0       ^∂ B 0               (0) *     i ∆ω t - i ∆ kz

+ v0    + δ0B0 = U B1 B2e,

∂t∂

∂B1 +v ∂B1 +δB =U(1)B*B ei∆ωt-i∆kz, ∂t     1 ∂z      1 10 2

∂B2 +v ∂B2 + δ B = U(2)B B ei∆ωt-i∆kz, ∂t      2 ∂z      2 20 1

U(j) = U(j)      , v = v , ∆ω= ω +ω -ω , k0k1k2 ;m0m1m2 j kj0 1 2

где v j и δ j – групповая скорость и инкремент неустойчивости j -й волны, U ^{( j )} – коэффициенты взаимодействия, й j - поляризационный вектор [3]. В линейном приближении при B j = const из (3), (4) следуют дисперсионные соотношения для мод.

Система (4) описывает широкий круг нелинейных явлений: формирование нелинейных структур [7, 8], различные виды вынужденного рассеяния волн на волнах иной природы [5], генерацию волн суммарной и разностной частот, возбуждение второй гармоники, параметрическое усиление [1, 8] и т. д.

Пренебрежём далее фазовой расстройкой ( ∆ω = ∆ k =0). Положим B j = b j exp( i ψ j ) и будем, следуя [3], полагать разность фаз постоянной ψ 2 - ψ 1 - ψ 0 = π/2 .

При этом система (4) преобразуется к виду

∂b0 1 ∂b0

+       + ζ ₀ b ₀ = V b ₁ b ₂ ,

∂ z v ₀ ∂ t

∂b1 + 1 ∂b1 + ζ1b1 =V(1)b0b2 ,(5)

∂ z v ₁ ∂ t

∂b2 1 ∂b2(2)

+ +ζ b = V bb ,

2 20 1

∂z v2 ∂t где ζj = ζkj = δj /vj – пространственный инкремент, V (j) = U (j)/vj.

Результат взаимодействия зависит от целого ряда управляющих параметров – коэффициентов взаимодействия волн, величин фазовой и групповой расстроек, наличия или отсутствия неустойчивостей.

Здесь рассматривается задача формирования одномерных и спиральных структур при параметрическом взаимодействии волн.

2. Одномерные структуры

В этом разделе исследуются особенности формирования радиально-однородных структур, соответствующих значениям азимутальных волновых чисел m 0 = m 1 = m 2 =0 при параметрическом взаимодействии.

Будем в дальнейшем считать волну с индексом «2» волной накачки, распределение амплитуды волны накачки однородным b ₂ ≈ b ₂₀, а входной импульс субгармоники (волна с индексом «1») слабым b ₁( t ) << b ₂₀ . Будем считать также инкремент неустойчивости существенно меньше параметрического инкремента и для простоты положим ζ j =0.

В частном случае вырожденного по частоте трёхволнового взаимодействия ω 0 = ω 1 = ω 2 /2 система (5) сводится к паре уравнений:

^{∂ b 1} + 1 ^{∂ b 1} = V ⁽¹⁾ bb , ^{∂ b 2} + 1 ^{∂ b 2} = V ⁽¹⁾ b ².      (6)

∂ z    v ₁ ∂ t ^{2 1 ,} ∂ z    v ₂ ∂ t          ¹

Дополним систему (6) граничными условиями b 1 ( z = 0) = b 1 ( t ), b 2 ( z = 0) = b 2 ( t ).

Интегрируя следующее из (6) соотношение

ν 12

∂ ² b ₂

∂ξ 1 ∂ξ 2

2 V ⁽¹⁾ b ₂

∂ b ₂

∂ξ 1

вдоль характеристики ξ 1 = t – z/v 1 , получаем [1] уравнение Риккати:

ν 12 ^∂ b ² = V ⁽¹⁾ b 2 ² - F ( ξ 2 ).

∂ξ ₂

Выражая из первого уравнения системы (6) амплитуду b 2 и подставляя её в это соотношение, получаем линейное обыкновенное дифференциальное уравнение [1, 8]

2 - 1

∂ b 1 _{2 =} V (1) ν ₁ - ₂ 2 F _{(ξ 2 )} b ₁ - 1 ,

∂ξ ₂

решение которого хорошо известно. Здесь функция F ( ξ ₂) следует из граничных условий с учётом (6)

F ( ξ 2 ) = V ⁽¹⁾ b 1 ² ( ξ 2 ) + V ⁽¹⁾ b 2 ² ( ξ 2 ) - ν 12 ^∂ b ² .

∂ξ ₂

В частном случае однородного распределения амплитуды волны накачки b ₂ ≈ b ₂₀, и малой амплитуды субгармоники b 1 ( t ) << b 20 решение системы (6)

имеет вид b1 =

b1(ξ1)

e z + shM. j d n b ^ -n ) e -w^т _c τ C b 20 0

Здесь Γ0 = V(1)b20, – параметрический инкремент, τС = ν21Γ0-1, νij = vi-1 -v-j1 – расстройка групповых скоростей взаимодействующих волн.

Из решения (7) следует, что после нарастания амплитуды субгармоники b1 до амплитуды волны на- качки b20 наступает нелинейный этап взаимодействия волн, протекание которого сильно зависит от профиля фронта субгармоники [1, 8].

При постоянной амплитуде b1 = b10 = const получаем b1 = b10

b2

exp (-V(1)b20z ) + -^s sh ( V(1)b20z)

2 b20

На длине L 0 = Γ 0 ^{– 1}ln(2 b 20 /b 10 ) амплитуда субгармонического сигнала достигает максимума b _1max ≈ b ₂₀, а при z > L 0 уменьшается – начинается генерация волны накачки.

Если субгармонический сигнал имеет экспоненциальный фронт b 1 ( ζ 1 ) = b 10 exp(– ζ 1 / τ 1 ), то ситуация меняется принципиально. При рассогласовании групповых скоростей ν 12 ≠ 0, когда v 1 > v 2 , характер энергообмена между субгармоникой и волной накачки различен для переднего и заднего фронтов усиливаемой волны. Практически вся мощность накачки поглощается передним фронтом, а задний фронт обостряется за счёт нелинейных потерь, связанных с удвоением частоты субгармоники. Дальнейшая эволюция сигнала зависит от соотношения между начальной крутизной фронта τ 1 и критической длительностью сигнала τ C .

При τ С <  τ 1 на отрезке 0 < z < L 0 , возмущение нарастает с линейным инкрементом Γ ₀. При z = L ₀ амплитуда субгармоники достигает значения b 1 = b 20 , а на нелинейной стадии эволюции при z > L ₀ завершается формирование заднего фронта волны.

При τ С >  τ 1 на нелинейной стадии эволюции при Γ 0 z >>  1 происходит формирование квазистационар-ного импульса вида

1/2 , Tc I + — I sec

T )

( h|r z-^1

I T

^b1 ( z , t ) ” b 20 I ¹

которое завершается на длине

L ≈ 1 ln

2 b ₂ ² ₀ ( τ ₁ +τ _C ) b 1 ² 0 τ 1

> L ₀ .

Таким образом, амплитуда импульса при τ _С >  τ ₁ превышает амплитуду волны накачки и образуется так называемый гигантский параметрический импульс [1, 8, 9]. В частности, в оптических средах формирование такого импульса рассматривалось в [9]. Очевидно, что учёт усиления ζ j ≠ 0 приводит к увеличению полного инкремента и сокращению длины формирования стационарного импульса L. Однако вопрос о стабилизации возмущения в этом случае должен решаться отдельно.

Отдельным классом решений системы (6) являются автомодельные решения вида бегущих волн b j = b j ( ς ) , где ς = t – z/w . В этом случае уравнения (6) принимают вид

ν d b ¹ = V ⁽¹⁾ bb , ν d b ² = V ⁽¹⁾ b ², (8) ¹ d ς ^{1 2 2} d ς ¹

где vj = 1 – w/vj. Систему (8) нетрудно свести к одному уравнению. Умножая первое уравнение на b1, а вто- рое – на b2 и вычитая второе из первого, имеем соотношение v1 b2 — v2b2 = const, используя которое легко

получить искомое уравнение, имеющее решение вида

b i ( ? ) = b io ^sec h I - I , ^b 2 ( ? ) = ^b 20^th I - I , I т )                 IT )

где v 1 v ₂ = V ⁽¹⁾² b ^T ², v 1 = V ⁽¹⁾ b ₂ ² ₀ t [1]. Исключая отсюда

скороcть w, получаем связь между амплитудами волны накачки и субгармоники b20 = b20 + (v12b20)/(V(1)т). С

учётом этого выражения имеем

1/2

sec h

( T _ 1 ^b 1 ( ? ) = ^b 20 I ^{1 +} — I I T )

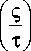
где t C = v 12 / V ⁽¹⁾ b 20 . Амплитуда субгармоники превышает амплитуду волны накачки при условии v ₁₂ b ₂₀ >  0 . При этом условии формируется параметрический импульс, описанный выше. Из приведённого решения, в частности, следует, что при вырожденном взаимодействии уединённая волна существует только на частоте ® 1 .

В невырожденном случае, как и выше, при т ^ 0 может формироваться гигантский параметрический импульс, амплитуда которого превышает амплитуду волны накачки, причём при v ₀₂ v ₁₂ >  0 только на одной из частот, сигнальной или холостой, а при v ₀₂ v ₁₂ <  0 и на сигнальной, и на холостой [1, 8].

Наибольший интерес, как и ранее, представляют решения системы (5) вида бегущей волны. В результате получаем консервативную систему db0      (0)

v0 V b1b2, d?

вующих значениям азимутальных волновых чисел m ₀ = +1, m ₁ = –1 и радиально однородной волны накачки m 2 = 0, представляющего интерес для ряда прикладных задач [5 –7].

Будем интересоваться решениями системы (5) вида бегущей волны. Очевидно, что система укороченных уравнений, описывающих бегущие волны, будет снова иметь вид (9), а её решение – вид (10).

Для того чтобы получить наглядное представление о форме возникающих в этом случае стационарных спиральных структур, удобно записать в соответствии с подходом [7] систему уравнений для компонент вектора отклонения средней линии вихря 5 = ( 5 , П , Z ) от оси r = 0 в поле возмущённого потока (3) в цилиндрической системе координат. Например, для базовой системы уравнений Эйлера, исследуемой в [7], получим

d t

.

и Ф 0 д| r дф

⁺ u_z 0

-

— = К ( и ₀, и ) , д z

где и₀ = ( 0, и _{ф 0}, u_{z 0} ) - невозмущённое поле,

— / — — \ | v d | u ф 0 ] v ^d uzO I 8 ( и 0 , и ) = Ur , и ф +Z r —I — I , Uz +Z — .

d r I r )          d r

v, d b = V ⁽¹⁾ b₀b ₂, d ?

d b ₂       (2)

^v 2 V   b 0 ^b 1^.

^d ?

Считая волну с частотой to 2 волной накачки, находим решение системы (9):

b ( ? ) = j sech (?/ ^т ) , ^b 2 ( ? ) = ^b 20^th (?/ ^T ) , j= 0; 1, ⁽¹⁰⁾

где скорость волн и их амплитуды согласно [1] опре-

деляются соотношениями

₂ 1/2

w-¹ = v ₀ ^—1 - ^ ± I V ⁽⁰⁾ V ⁽¹⁾ T ² b ₂• + ^ 1 I

⁰ 2 I ²⁰ 4 )

2 V (j) 21 ^bj ⁰    V (2) ^{b 20} I ^{1 +}

Ум

₂ 1/2

± I v ⁽⁰⁾ v ⁽¹⁾ т ² b ₊ Y °i I

2 I ²⁰ 4 )

Полученные в разделе результаты будут использованы далее при исследовании спиральных структур.

3. Вихревые структуры

В этом разделе исследуются особенности формирования вихревых структур для частного случая из-гибных субгармонических возмущений, соответст-

Разыскивая вектор отклонения средней линии вихря в форме спиральной волны Z = Z ₀ ( r ) exp ( ikz + im ф — i to t ) и подставляя в (11) выражения для возмущений скорости из (3), (10), получим в соответствии с [7] для амплитуды отклонения выражение вида

^— iR — -

S 0 =-- ( ^bj^u +^ 0 ) ,

^V ф 0

где R – радиус цилиндрического волновода, а вектор Е0 равен d ( иф0 ) е duz0 ) ф             z°-

0 r J I I , ^ 0 J .

d r | r )     d r )

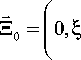
Декартовы компоненты вектора отклонения связаны с компонентами вектора ^ для мод m = ± 1 соотношениями Х= 5, cos ф - n sin Ф , Y= Z sin Ф ⁺ П cos Ф - Вводя безразмерные координаты x = X / ^ , y = Y / ^ , где ^ = R ( v ₂ и 2 (0)/ v 1 и 2 (0))^1/2, и следуя методике, подробно описанной в [7], при to 2 = 2 to 1 и малой начальной амплитуде моды b 1 ( t ) <<  b 2 , приходим к уравнению вихря в параметрической форме. Для фиксированного момента времени, например для t =0, имеем уравнение спирали с амплитудой b ₂₀sec h ( в и ).

x = b20 sec h (в и) cos (а и), x = b20sec h (ви) sin (аи),                          (13)

z = и, где а =1- v 1, в = b20/T, T-1 = U*)/v 1.

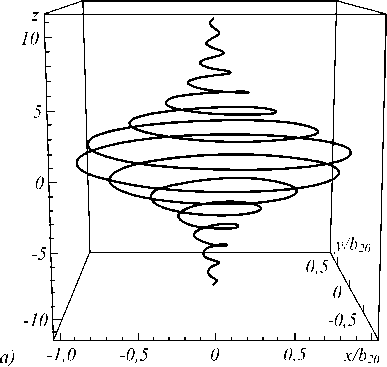
Таким образом, в среде формируется вихревая солитоноподобная структура, представляющая собой спираль, ограниченную огибающей радиуса, максимальное значение которого равно b 20 (рис. 1). При z ^ ± ^ значение радиуса огибающей стремится к нулю. Кривизна и кручение винтовой линии равны соответственно

^К 1

b 20 sec h (в z)         _ а а2 + b220 sech2 (вz) ’ 2   а2 + b20 sech2 (вz)

-5 о____।_____।_____।_____I____।_____।_____।____।_____I_____।____।_____।____।_____I_____।____।_____।____i—у б)

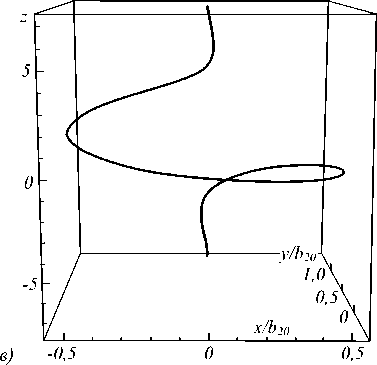
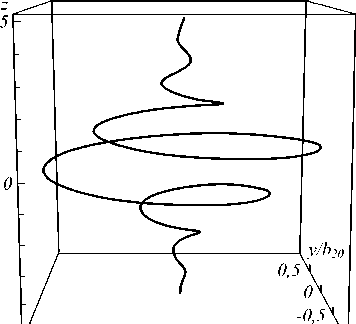
Рис. 1. Форма уединённой волны при α = 4, β = 0,4 (а), α = 4, β = 1 (б), α = 4, β = 4 (в)

При b ₂₀ ^ 0 спираль переходит в прямую линию.

Форму вихревой структуры, как следует из соотношений (13), определяют параметры α и β. Характерная длина солитона ~ β^–1 определяется из условия уменьшения поперечного размера в е раз. Количество витков спирали n на характерном размере уединённой волны в докритическом диапазоне параметров β < β C равно β/α. Значение β C зависит от вида системы (2).

При β < β C безразмерные координаты x и y являются однозначными функциями z и на длине уединённой волны укладывается конечное число витков спирали (рис. 1 а, б ) (область I параметрической диаграммы).

При β > β _C происходит перехлёст кривой и в проекции на плоскость ( х, у ) возникает замкнутая петля, которой при любых значениях параметра α соответствует однопетлевая структура (рис. 1 в ) (область II параметрической диаграммы). Параметрическая диаграмма режимов существования различных форм уединённых спиральных волн приведена на рис. 2.

Заключение

Таким образом, в работе показана возможность формирования петлевых и спиральных трёхмерных структур, ограниченных огибающей, появляющихся в активных нелинейных средах в результате резонансного взаимодействия трёх волн (рис. 1). В частности, показано, что при достаточно больших амплитудах волны накачки может возникать петлевая уединённая структура, совпадающая по форме с солитоном Ха-

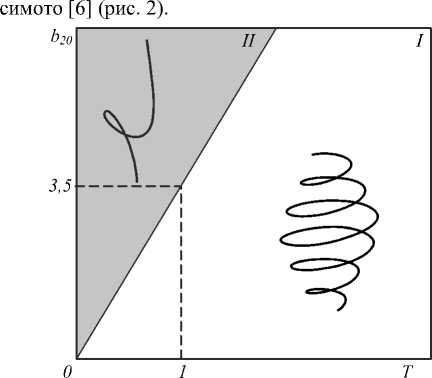
Рис. 2. Параметрическая диаграмма для спиральных структур системы (11)

Близкие по форме структуры были получены теоретически и ранее, однако либо как решения уравнений Серре–Френе для вихревых нитей [6], либо как односолитонные решения нелинейного уравнения Шредингера для изгибных гидродинамических волн [7].

Интересно отметить, что солитоноподобные газоплазменные петлевые структуры ВЧЕ-разряда наблюдались экспериментально в закрученном потоке в аргоне [10] при возбуждении в трубке акустического поля большой амплитуды на первой резонансной час- тоте, соответствующей значению азимутального числа m2 = 0. Однако этот вопрос требует дальнейшего анализа, и ему будет посвящена отдельная работа.

Работа частично поддержана Минобрнауки РФ в рамках Программы повышения конкурентоспособности СГАУ на 2013 – 2020 гг., Государственного задания вузам и научным организациям в сфере научной деятельности, проекты № 102, 608 и грантом РФФИ 13-01-97001 р_поволжье_а.