О формуле Карлемана

Актуальность темы. Известно, что вопрос восстановления своих значений внутри сферы, зная его значений в границах сферы, является одним из актуальных вопросов индексного анализа, и изучению этой темы посвящено немало научной литературы и статей. На плоскости этот вопрос решается интегральной формулой Коши, учитывая, что значения функции задаются вдоль всей границы сферы. Задача усложняется, если значения функции задаются не во всей границе поля, а только в некоторой его части. Если этот вопрос рассматривать в многомерном комплексном пространстве, то он становится еще более сложным.

Интегральное отображение голоморфных функций играет важную роль в классической теории комплексных переменных функций и в многомерном комплексном анализе (во втором случае происходит интеграция D по всей границе области д D , а также интеграция S = S ( D )

по границе Шилова). Они решают классическую проблему восстановления голоморфных функций при приближении к границе д D по значениям в точках D области д D или S . Помимо этого классического вопроса, естественно, можно рассмотреть следующий вопрос: восстановление голоморфной функции в D по значениям в наборе M ⊂∂ D, которые не существуют в S . Конечно, M - это должен быть уникальный набор для рассматриваемого класса голоморфных функций (например, непрерывный в D или один из классов H^p ( D ), p >  1 Харди).

Обзор (анализ) литературы по теме исследования. Т . Карлеман добился для сферы D g С определенного вида. В 1933 году Г.М.Голузин и В.И.Крылов развили идею введения в интегральную формулу Коши функции “ вспомогательной ” функции для одноцепочечных сфер (см., например, [1]). Их способ подразумевал построение некоторой вспомогательной голоморфной функции, связанный с набором M , что возможно для одноцепных областей D g C ¹, но неуместно для многоцепных областей в или для областей в С n , n >  1 . Другой метод, основанный на приближении аппроксимации ядра в интегральном виде, был предложен в 1956 г. М. М. Лаврентьевым. Оказалось, что этот метод хорошо работает, когда метод Голузина-Крылова не может быть использован в указанных случаях.

Нахождение формулы Карлемана для однородных сфер было предложено А.М. Китмановым. Формулы Карлемана находят свое применение при решении задач, когда заданная функция на границе поля может быть голоморфно продолжена до поля ( Например, см. [2-3, 1-4]).

Формула Карлемана в комплексном анализе одной переменной изучалась Г. М. Голузиным, В. И. Крыловым, М. А. Лаврентьевым, А. М. Китмановым и другими учеными и до сих пор изучается несколькими учеными. Метод Голузина-Крылова доказал, что формула Карлемана подходит для областей с одной связью D и гладкой границей дD (см. [2]).

1-Теорема. Если f е Н^р ( П ), 1 <  р < ю , ва M о R ¹ = дП мера Лебега положительна, тогда для точки V е П формула Карлемана с плоским приближением в полученных компактах от П является подходящей:

f ( z ) = ^ ft ( t ) ^{2 n i} M

m

ф ⁽ t )

dt

_ ^(z) J t - z

.

Доказательство. Доказательство этого дается таким образом и приводится к интегральной оценке:

J m = J f ( t ) ^{2 n} i R \ M

ф ⁽ t )

m dt

_ ^ ( z ) J t - z

.

Функция |^(t)| почти во всех местах набора r 1 \ m равен 1; поэтому применяя неравенство Гёлдера (2) образуем интегральную оценку для

_       .     1 , 1  1

интегральной модули —+ — = 1, р >  1:

pq

1 J |5 —1— mm 2 п|^ ( z )		1\ p		1\ q
	j I f ( t )| p dt _ R * \ M             _		f    dt
			j _ R * \ M t   z | _

Кроме того, при m ^ ю выходит, что компакты, полученные от П выходят плоскими Jт ^ 0. Если р = 1, тогда

I ^J m | ⁵

2 n|^ m Inf | t - z| t е R * \ M

j | ^{f (} t )| dt , R * \ M

И опять компакты, полученные от П в m ^ ю _мы создаем _{плоское} стремление J m ^ ⁰.

Данная теорема не применяется не только из-ща того, что из-за отсутствия оценки при р = ю не только в случаях (3) или (4), но в первую очередь из-за отсутствия интегральной формулы Коши для класса функции

Н ” (П).  Но в этом случае уместна формула Пуассона:  если f е Н (П), 1 < р < ^ , тогдя для z е П

+^

y^{f (} t ) dt

( x - 1 )² + y ²,

f (z ) = -J п

-ю

Ядро Пуассона является абсолютным интегратором в R1 , он аналогичен методу Карлемана, то есть следующая теорема легко выводится тем же методом:

2 - Теорема.     Пусть f е Н^р ( П ), 1 <  р <^ и мра Лебега набора

M положительна, тогда для z еП уместна следующая формула:

m f (z) = lim1 f f (t) ^  ---ydt---.

m ^п MM    L ^ ⁽ z ) J ⁽ x ^- t ) + y

Его лимит в компактах, полученных от П приближается плоско.

Чтобы рассмотреть многомерные случаи формул Карлемана, целесообразно расширить функции, в которых эти формулы подходят для полуплоскости П. Пусть f е Л(П), нужно отметить, что f i у 1 + (У у

е Н^р (U (0,1)) уместно только если

-( z^ е H ^p ( П )^{, 1} <  р <«

^{( z +} t )

уместно.

Основные направления исследований Карлемана — интегральные уравнения и теория функций. Многие его труды опередили своё время и поэтому были не сразу оценены по достоинству, но теперь рассматриваются как классические.

Диссертация Карлемана и его первые труды в начале 1920-х годови был посвящены сингулярным интегральным уравнениям. Он разработал спектральную теорию для интегральных операторов с «ядром

Карлемана», то есть таким ядром K(x, у) , что K(y, x) = K(x, у) для почти всех (x, y), и при этом:

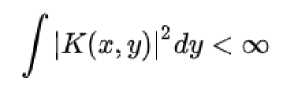
для почти каждого х.

В    середине    1920-х    годов    Карлеман    разработал теорию квазианалитических функций. Он доказал необходимое и достаточное условие квазианалитичности, которое теперь называется теоремой Данжуа–Карлемана. Как следствие, он получил «условие Карлемана» — достаточное условие для определённости проблемы моментов. Как один из шагов в доказательстве теоремы Данжуа– Карлемана (1926), он представил неравенство Карлемана:

ОО                            ОО

(°1°2 •••йп)1/п ^ еУ2^М

71=1                       П=1

справедливые

для

любой

последовательности

неотрицательных вещественных чисел {\displaystyle a_{n}}. Ввёл понятие «континуума Карлемана».

Примерно в то же время он установил «формулы Карлемана»

в комплексном анализе, которые, в отличие воспроизводят аналитическую функцию в области части границы (с ненулевой мерой Лебега). обобщение формулы Йенсена, которое теперь часто Йенсена — Карлемана.

от

по

Он

формул Коши, её значениям на

также доказал

называется формулой

В 1930-е годы, независимо от Джона фон Неймана, Карлеман обнаружил вариант эргодической теоремы (the mean ergodic theorem). Позднее он занимался теорией дифференциальных уравнений в частных производных, где представил «оценки Карлемана», причём нашёл способ изучить спектральные асимптотики операторов Шрёдингера.

В 1932 году, развивая работы Анри Пуанкаре, Эрика Ивара Фредгольма и Бернарда Купмана, он разработал встраивание Карлемана (также называемое линеаризацией Карлемана). Карлеман также впервые рассмотрел граничную задачу аналитических функций со сдвигом, изменяющим направление обхода контура на обратное («граничная задача Карлемана»).

В 1933 году Карлеман опубликовал короткое доказательство того, что сейчас называется теоремой Данжуа — Карлемана — Альфорса. Эта теорема утверждает, что число асимптотических значений, принимаемых целой функцией порядка ρ вдоль кривых на комплексной плоскости в направлении к бесконечной абсолютной величине, меньше или равно 2ρ.

В 1935 году Карлеман представил обобщение преобразования Фурье, которое стимулировало последующие работы Микио Сато о гиперфункциях; его заметки были опубликованы в Carleman (1944). Он рассмотрел функции f {\displaystyle f}ff++f1 не более чем полиномиального роста и показал, что каждая такая функция может быть разложена как f++f- {\displaystyle f_{+}+f_{-}}, где слагаемые являются аналитическими в верхней и нижней полуплоскостях соответственно, причём представление является по существу единственным. Затем он определил Фурье-образы {\displaystyle f_{+},f_{-}} f++f- как ещё одну такую пару g+, g-{\displaystyle g_{+},g_{-}}ggg. Это определение соответствует тому, что дано позднее Лораном Шварцем для обобщённых функций медленного роста, хотя концептуально от него отличается. Подход Карлемана вызвал множество работ, расширяющих его идеи.

Вернувшись к математической физике в 1930-е годы, Карлемана дал первое доказательство глобального существования для уравнения Больцмана в кинетической теории газов (его результат относится к пространственно-однородному случаю). Эта работа была опубликована посмертно в Carleman (1957).

ЛИТЕРАТУРЫ:

• 1.    Голузин Г.М., Крылов В.И. Обобщенная формула Карлемана и ее приложение к аналитическому продолжению функций // Мат. Сб. 1933. Т.40. №2. с.144-149.

• 2.    Л.А.Айзенберг. ,,Формулы Карлемана в комплексном анализе’’ . Новосибирск, Н:,1990 г, 248с.

• 3.    Г.Худойберганов, А.М. Кытманов, Б.А.Шаимқулов. ,,Комплексный анализ в матричных областях’’ Кроснаярск, 2011 г. 290 с.

• 4.    Кытманов А.М, Никитина Т.Н. ,,Анологи формулы Карлемана для классических областей’’ ,Мат.заметки 1989 г. 153 с.

• 5.    Худойберганов Г., Матякубов З.К., Куромбоев Х.Н. Формула Карлемана для матричного шара второго типа. Труды конф. “Актуалные проблемы прикладной математики и информационных технологий-Аль-Хорезми 2014”, Самарканд, 15-17 сентябр, 2014, ст. 247-248.

• 6.    Куромбоев Х.Н., О формуле Карлемана. Научная конф. “Неклассические уравнения математической Физики приложения, Ташкент 2014”, Ташкент, 23-25 октября, 2014, ст. 237-238