О геометрически нелинейных определяющих соотношениях упругого материала
Автор: Трусов П.В., Кондратьев Н.С., Швейкин А.И.
Статья в выпуске: 3, 2015 года.
Бесплатный доступ
В задачах механики деформируемого твердого тела часто возникает необходимость использования определяющих (физических) соотношений в скоростной форме, например, при формулировке в скоростях постановки краевой задачи с контактными условиями, когда области контакта априори неизвестны и изменяются в процессе деформирования. В статье рассматриваются некоторые вопросы построения геометрически нелинейных определяющих соотношений упругого материала в скоростной форме, а также взаимосвязь этих соотношений с определяющими уравнениями в конечной форме. Во многих существующих моделях упругих и упругопластических тел в качестве определяющего соотношения используется закон Гука, записанный в терминах актуальной конфигурации. В качестве скоростной меры деформированного состояния, как правило, принимается тензор деформации скорости, а напряженного - некоторая не зависящая от выбора системы отсчета производная (конвективная или коротационная) взвешенного тензора напряжений Кирхгоффа. Вследствие определенных сложностей при использовании конвективных производных (например, трудностей анализа эволюции изменения напряженного состояния по компонентам тензора в деформируемом базисе) они из рассмотрения исключены. Использование вместо материальной производной (по времени) тензора напряжений его коротационной производной позволяет удовлетворить принципу материальной индифферентности (независимости определяющего соотношения от выбора системы отсчета), однако выбор вида производной может быть осуществлен множеством способов. Произвольный выбор коротационной производной меры напряжений приводит к нежелательным эффектам: осцилляциям напряжений при монотонной деформации простого сдвига (например, для производной Зарембы-Яуманна), «незамкнутости» траекторий напряжений и отличию от нуля работы напряжений на замкнутой траектории деформаций. В работах A. Meyers, H. Xiao, O. Bruhns предложена коротационная производная (спин которой в литературе носит название логарифмического спина), обладающая следующим свойством: эта производная от правого тензора деформации Генки в точности равна тензору деформации скорости. При использовании этой производной в определяющем соотношении описанные эффекты отсутствуют, на основании чего предложившие ее авторы констатируют ее исключительность, рекомендуя только ее к использованию в определяющих соотношениях в скоростной форме.
Коротационные производные, скоростная и конечная форма определяющих соотношений, закон гука, коротационное интегрирование, независимость от выбора системы отсчета
Короткий адрес: https://sciup.org/146211570
IDR: 146211570 | УДК: 539.3 | DOI: 10.15593/perm.mech/2015.3.13
Текст научной статьи О геометрически нелинейных определяющих соотношениях упругого материала
PNRPU MECHANICS BULLETIN
Введение и основные понятия
Проблема построения определяющих соотношений для случая геометрической нелинейности в последние десятилетия является одним из весьма значимых направлений развития механики деформируемого твердого тела (МДТТ). Это вызвано как необходимостью дальнейшего развития теории механики деформируемого твердого тела, так и потребностями практики: в промышленности постоянно повышаются требования к качеству материалов и готовой продукции, следовательно, к качеству математических моделей технологических процессов, для корректного описания многих из них необходим учет геометрической нелинейности. Обзор литературы по данной проблеме можно найти в монографиях [1–3].
По мнению авторов, при построении определяющих соотношений в терминах отсчетной конфигурации (такие соотношения описываются, например, в работах [3, 4]) возникают некоторые проблемы с физическим анализом как самих соотношений, так и входящих в них мер деформированного и особенно напряженного состояния. При построении определяющих соотношений в терминах актуальной конфигурации эти вопросы частично снимаются по отношению к мере напряженного состояния: тензор напряжений имеет ясно выраженный физический смысл.
Для ряда задач МДТТ имеется насущная потребность в формулировке определяющих соотношений в терминах актуальной конфигурации в скоростях. Например, это необходимо при постановке контактных краевых задач, когда изменяющаяся область контакта определяется в процессе решения задачи [3]. Можно также отметить, что постановки краевых задач в скоростной форме более удобны для применения численных методов, например метода конечных элементов [5, 6], когда решение задачи осуществляется пошагово, в приращениях [3]. Поэтому в последние десятилетия весьма популярными являются определяющие соотношения (ОС) в скоростной форме, сформулированные с использованием мер напряженно-деформированного состояния (НДС), определенных в текущей конфигурации.
При построении таких соотношений, помимо вопроса выбора мер НДС (скоростей мер НДС), актуальной является проблема выбора не зависящей от системы отсчета производной [3, 7–9]. Действительно, в отличие от случая использования в ОС материальной производной применение любой не зависящей от выбора системы отсчета производной позволяет удовлетворить принципу материальной индифферентности (принципу независимости определяющего соотношения от выбора системы отсчета [10, 11, 3]), однако различный выбор вида производной приводит к существенным (зачастую – качественным) отличиям получаемых НДС.
В общем виде не зависящая от выбора системы отсчета производная Qr тензора вто- рого ранга Q определяется выражением Qr (qi) =
d ,
—( q • Q • q j ) q^ j ,
. dt J
k где q i , q k
соот-
ветственно векторы основного и сопряженного базисов подвижной системы координат (СК). Образно говоря, подвижный наблюдатель в каждый момент времени фиксирует мгновенные изменения компонент тензора и относит их к своему базису, считая его неизменным. Таким образом, использование независимых от выбора системы отсчета производных подразумевает разделение движения на две составляющие: квазитвердое движение подвижной СК с базисом q i и собственно деформационное движение (относительно этой подвижной СК), мера скорости которого связывается в ОС со скоростью изменения напряженного состояния. Очевидно, что выбор подвижной СК и, соответственно, коротационной производной можно осуществить множеством способов. Наиболее известные и часто используемые в работах по механике сплошной среды не зависящие от выбора системы отсчета производные рассмотрены в [4, 12–14, 3 и др.].
Базисы для конвективных производных являются деформируемыми (например, для производной Олдройда [12] и Коттер–Ривлина [13] подвижный базис – текущий лагранжев), что, по мнению авторов, приводит к неясности в определении тензора напряжений и невозможности анализа изменения длин материальных отрезков и углов между ними (которые наблюдаются из неподвижной лабораторной системы отсчета, но не «ощущаются» подвижным наблюдателем), равно как к сложностям отделения изменения компонент мер напряженного состояния, определяемых процессом деформирования, от их изменения из-за деформирования базисных векторов. Поэтому далее рассматриваются только коротационные производные (с ортонормированным базисом подвижной СК).
Известно, что произвольный выбор коротационной производной меры напряжений приводит к нежелательным эффектам: осцилляциям напряжений при монотонной деформации простого сдвига (например, для производной Зарембы–Яуманна [3]), «незамкнуто-сти» траекторий напряжений и отличию от нуля работы напряжений по замкнутой траектории упругих деформаций.
В работах [15, 16] предложена коротационная производная (ее спин назван логарифмическим), обладающая следующим свойством: эта производная от правого тензора деформации Генки в точности равна тензору деформации скорости. На основании того, что при использовании этой производной в определяющем соотношении упругого (важно обратить внимание) изотропного материала описанные эффекты отсутствуют (соответствующие результаты приводятся, например, в работе [17]), авторы логарифмического спина рекомендуют только его к использованию в определяющих соотношениях в скоростной форме, причем не только для упругого материала – в работе [18] логарифмический спин предлагается использовать в модели упругопластичности.
Отметим, что построение геометрически нелинейных ОС особенно затруднительно для физически нелинейных материалов, например упругопластических и упруговязкопластических [1–3]. Следует отметить, что при значительных деформациях в поликристалли-ческих металлах и сплавах происходит процесс текстурообразования, что приводит к появлению анизотропии свойств, в связи с чем обоснованность применения логарифмического спина в соотношениях макроуровня вызывает определенные сомнения. В последние десятилетия при формулировке геометрически и физически нелинейных соотношений все большую популярность приобретает многоуровневый подход, основанный на введении внутренних переменных [19–22]. В моделях авторов предлагаемой статьи, построенных в рамках этого подхода с явным описанием внутренней структуры и механизмов деформирования, формулируются соотношения на низшем масштабном уровне (на уровне кристаллитов используется закон Гука в скоростной форме [23]), соотношения макромасштабного уровня получаются путем проведения процедуры согласования ОС масштабных уровней [23]. Таким образом, при применении многоуровневого моделирования одной из важных задач является корректное описание ОС на низших масштабных уровнях, в частности, для двухуровневых моделей материалов [23] – корректная формулировка геометрически нелинейного закона Гука.
В предлагаемой статье устанавливается связь между законом Гука для анизотропного материала в скоростной и конечных формах при условиях существования материального базиса, в котором компоненты тензора упругих свойств тела остаются неизменными, и использования однотипных коротационных производных от мер деформаций и напряжений. Также рассмотрены некоторые меры деформаций и их не зависящие от выбора системы отсчета скорости изменения, в том числе – получаемые с применением логарифмического спина. Приведены результаты вычислительных экспериментов для замкнутых циклов деформаций, которые показывают, что при соответствующем выборе мер НДС и мер их изменения для изотропных упругих материалов при любом выборе коротацион-ной производной наблюдается замкнутость траектории напряжений; если при этом на меры НДС накладывается условие энергетической сопряженности, то наблюдается и отсутствие диссипации энергии.
Полученные результаты свидетельствуют о недостаточной аргументации вышеприведенного утверждения об исключительной необходимости использования логарифмического спина и соответствующих скоростей мер НДС. По мнению авторов, при постановке и решении задач механики твердого тела должна иметься возможность использования различных мер НДС и их скоростей, при этом выбор мер и ОС должен быть обоснован с позиций физического анализа рассматриваемого процесса.
1. Меры деформации и их не зависящие от выбора системы отсчета скорости изменения
В настоящее время в нелинейной механике используется широкий спектр мер деформированного состояния. Распространение получило полярное разложение градиента места, с использованием которого вводится семейство мер Сетха [4]. В силу неособенно-сти градиента места его можно представить в виде скалярного произведения симметричного и ортогонального тензоров:
О v r = U • R = R • V, (1)
О где V(-) - набла-оператор, определенный в отсчетной конфигурации K0; r - радиус-вектор материальной частицы в актуальной конфигурации Kt; U, V – соответственно левый и правый тензоры искажения; R – ортогональный тензор, сопровождающий деформацию. Поскольку U и V симметричные положительно определенные тензоры, то для них существует тройка положительных действительных собственных чисел λi (кратность уд- линения) и тройки ортогональных векторов
О ( О ", )
P z P z = P
U
И P Z ( P z = P )
тензо-
ра V . В главном базисе U и V тензоры, входящие в (1), примут вид
-
3 О О 3 3 О О 3
U =ЕVPzP,, V =ЕMzpz, R=ЕP-P-,vr=ЕxzPzpz(2)
i=1 Z=1 Z=1
С использованием введенных тензоров U и V можно ввести широкий класс мер деформаций M и M [4, 3]:
О 3 О О О A 3
M = Е ln f ( U z ) P z P z , M = E ln f ( V z ) p z p z ,
Z=1
где f ( U z ) , f ( V z ) - монотонно гладкие функции удовлетворяющие условиям
О f (1) = f (1) = 0, f'(1) = f'(1) = 1.(4)
Введенное семейство мер включает в себя семейство мер деформаций Сетха:
М ()= — (U2 n -1), М(n )= — (V2 n -1),(5)
2n2n где I – единичный тензор. Определяющие соотношения удобно записать в актуальной конфигурации, где компоненты мер напряжений и деформаций имеют ясный физический и геометрический смысл. Вследствие этого для примера будут рассмотрены случаи, когда в качестве мер деформаций используются тензоры Альманси A и правый Генки Hˆ , а меры напряжений – тензор Кирхгоффа κ. Все компоненты упомянутых тензоров имеют явный геометрический и физический смысл. Следует отметить, что в отличие от пары тензоров κ и Hˆ , пара κ и A не является энергетически сопряженной. Тензоры A и Hˆ являются тензорами из семейства Сетха при n = –1 и n = 0 соответственно:
М ( - 1 ) =- 2 ( V - 2 - 1 ) = 2 ( I - V - 2 ) = 2 ( I - ( V - 1 • R T ) • ( R • V - 1 ) ) =
мера Аль-
1 ( О
= 1 1 I -v r - 1
• \7 r-T ) =1 (I -VRo -VRoT) =1 (l - G) = A, J 2\ 0 0 J 2\ / где V(-) - набла-оператор в актуальной конфигурации Kt; G = VR0 -VR0
О О О манси. Используя диадное представление градиента места V r = ez ez (ez, ez - взаимный базис лагранжевой системы координат в отсчетной и основной в актуальной конфигура-r \-1 / О \ О л ции), можно убедится, что IV r I = ez ez = VR0, R - радиус-вектор частицы в Kc. Правый тензор Генки Hˆ получается из семейства Сетха при n = 0. При раскрытии неопределенности типа ноль на ноль используется правило Лопиталя:
2 У X2n ln Xipipiз
PM(0) = limPM(n) = lim—(V2n -i) = lim-^1-----------= TinX,pД = In V = H.(7)
n^0 n^0 2n n «^0 2 fl
Для определения производной по параметру, входящему в степень, правый тензор искажения V записывается в главном базисе p ˆ i с собственными числами λ i , далее, учитывая независимость базисных векторов p ˆ i от степени, определялась производная компонент тензора V 2n в этом базисе.
В общем случае независимые от системы отсчета производные тензоров 2-го ранга (конвективные и коротационные), описывающие некоторые характеристики исследуемой частицы с ее ε-окрестностью, определяются соотношениями [3]
B r ( q i ) = dt ( q , • B • q j ) q , q j = ( q B • q v + q , •15 • q j + q B • qu) q i q j ,
Br (qi) = d(qi • B • q ) qiqj = (q • B • q j + qi • B • q j + qi • B • qj) qiqj, dtx где qi, qi – основной и сопряженный базисы подвижной системы координат (ПСК). Множественность способов выбора этого базиса определяет многообразие объективных производных. Отметим, что в настоящей работе рассматривается жесткая ортогональная система координат, связанная с материалом, поэтому различие между векторами основного и сопряженного базиса пропадает и соотношения (8)1 и (8)2 являются эквивалентными. Вопрос о выборе ПСК и определении скорости ее вращения ω является актуальной задачей, возможный подход к ее решению предложен в [24]. Не конкретизируя способ опре-• деления тензора to (ki = to • ki = ki • toT =-lki • го), но предполагая его существование, запишем в общем виде коротационную производную индифферентной тензорзначной (второго ранга) функции времени B:
B “ = B - to • B + B • to .
Далее рассматриваются три типа коротационных производных:
-
1) Зарембы-Яуманна [25, 26], ассоциированная с тензором вихря W = 2 ( \7 v T -\7 v ) ,
B W = B - W • B + B • W ;
-
2) Грина–Нагхди [27], ассоциированная со спином Ω над ортогональным тензором R из полярного разложения ( Q = R T • R ),
B Q= B - Q • B + B • П ; (11)
-
3) определяемая с помощью логарифмического спина Ω log [15, 16]:
B n g = B - Q iOg • B + B • Q iog . (12)
Первые две из перечисленных производных получили широкое распространение в механике сплошных сред, и способ их введения не вызывает вопросов в отличие от последней производной. Вследствие этого кратко остановимся на выводе соотношения для определения логарифмического спина, используя теорию, предложенную в [28, 29]. Ис- ходной задачей является определение тензора логарифмического спина Ωlog, такого, что коротационная производная правого тензора Генки Hˆ , ассоциированная с этим спином, дает в точности тензор деформации скорости D:
/X /X /X /X
H Qog = H + H • Q. - Q. • H = D . (13)
log log
Из соотношения (13) можно определить искомый тензор Ω log , для этого (13) записывается в базисе правого трехгранника p ˆ i :
•
A, - _ A - A A .
D y = / 'V3 # + ^ Vm H m - H im Q V +H m Q m g - Q^H m , (14)
λk где ΩV j – компоненты тензора скорости вращения базисных векторов pˆ относительно ЛСК в базисе этих же векторов; D j, Hˆ j– компоненты тензора деформации скорости и правого тензора Генки в базисе pˆ . Поскольку тензор Ωlog является кососимметричным, в любом базисе имеет шесть ненулевых, из которых только три независимые (Qiog = Qjog, Qi0g = 0). Искомые недиагональные компоненты (i' * j) определяются из (14):
H jj - H ii ) +Q 10 g ij ( H ii - H jj ) , i * j , (15)
или при неравенстве главных значений H ii * H j можно записать
D
Q . j = q v j + ^-j^- , i* j . (16)
H ii H j-
Следует заметить, что на этом можно было бы остановиться и при определении логарифмического спина пользоваться (16). Однако при решении практических задач удобнее работать с компонентами тензоров деформации скорости и вихря (чем, например, с компонентами спина Ω V ); компоненты тензора Ω V через компоненты W и D в базисе p ˆ i можно определить следующими соотношениями [3]:
Q
V ij
= W
' r 2 + X 2?
x J
D j , i * j ,
где W ij – компоненты тензора вихря в базисе p ˆ i . С учетом (28) имеем
Q, = W + log ij ij
A A
H ii - H
r 2 + r 2 r 2 - r2
D j , i * j
или
Qiog j- = W j +
-
D j , i * j ,
где th ( • ) - гиперболический тангенс. Выше использована связь компонент тензора Генки с главными значениями тензора V : H ii = ln X i . Физический смысл компонент логарифмического спина, в отличие от смысла компонент тензора вихря и «материального» спина И = R T • R , непрозрачен. К сожалению, авторы цитируемых статей его не обсуждают.
-
2. Связь определяющих соотношений закона Гука в скоростной и конечной форме
Покажем, что для класса материалов с подвижным базисом, в котором компоненты тензора упругих характеристик материала не меняются (для изотропных материалов это выполняется в любой системе отсчета) в процессе деформирования, формы закона Гука в скоростном и конечном виде полностью эквивалентны. Это, в свою очередь, означает, что в скоростном виде для «замкнутости» траекторий напряжений при замкнутых траекториях деформации достаточно взять от меры деформаций и напряжений одинаковые ко-ротационные производные. Вследствие этого появляются определенные сомнения по поводу предпочтительности выбора в качестве скоростных мер тензора деформации скорости и логарифмической коротационной производной тензора напряжений Коши. Помимо сложности вычисления логарифмического спина, существует более значимый недостаток этой производной – отсутствие явной связи с материалом.
Рассмотрим закон Гука в конечной форме для монокристаллического материала в следующем виде [10]:
κ = п: ζ , (20)
где κ – взвешенный тензор напряжений Кирхгоффа; ζ – некоторый тензор деформации, определенный в актуальной конфигурации; п – тензор упругих свойств монокристалла.
Несколько «забегая вперед», отметим, что тензор напряжений Кирхгоффа использован здесь скорее как дань традиции, сложившейся при формулировке ОС гипер- и/или гипоупругих материалов. В общем случае в качестве меры напряжений может быть введен некоторый индифферентный тензор напряжений, определенный в базисе актуальной конфигурации; в частности, на определение этого тензора могут быть наложены дополнительные ограничения, например энергетическая сопряженность с коротационной производной, используемой в скоростной форме ОС. Последнее требование вводится при использовании термодинамического подхода к построению определяющих соотношений; в настоящей работе, ориентированной на применение макрофеноменологического подхода, указанное ограничение не вводится.
Найдем полную (материальную) производную от левой и правой части соотношения (20), при этом в общем случае тензор упругих свойств зависит от времени, п ( t ) (даже если его компоненты в том или ином подвижном базисе являются константами):
к = П : Z + п : Z . (21)
Введем две системы отсчета: лабораторную условно неподвижную систему координат (ЛСК) с ортонормированным базисом ki и жесткую подвижную систему координат (ПСК) с ортонормированным базисом ki (ki = k1); здесь и далее черта сверху обозначает величины, определенные в ПСК. Без ограничения общности можно считать, что обе сис- темы в начальный момент деформирования совпадают. Полагается, что ПСК связана с материалом, поэтому компоненты тензора упругих свойств в этом базисе остаются неизменными. Связь векторов базиса ПСК и ЛСК описывается ортогональным тензором •
Т\ __T
o ( t ): k i = о • k i , откуда получаем k i = о • k i = ( o • o ) • k i = wk i = k i -ш = - k i -ш , ш = o • o спин ПСК относительно ЛСК. Рассмотрим первое слагаемое правой части (21):
—
-
п : z = п„ , k i k j k p k q : Z" k , k t + п .k - k j k p k q : Z" k , k , +
+ j k k k p k q :Z rt k r k , + j k i k k p k ' : Z" k k t =
= j ( ш • k i ) k k p k ' : Z rt k r k t + j k i ( ш • k j ) k p k q : Z 't k , k , + + п„ pq И ' ( « • k p ) k q : Z 't k , .k t + j k i k j k p ( ш • k q ) : Z 't k , k t = = ш • п jpq Z qp k - k j + пwZ qp k - k j • ш т + п №q Z qt k - k j ( ш • k p ) • k t + + п „р, Z 'p k - k j ( ш • k q ) • k r .
Для преобразования двух последних слагаемых следует напомнить, что используется ортонормированный базис, т.е. справедливо k i • k j = 8/ (8/ — дельта Кронекера).
• •
Дифференцируя последнее соотношение, имеем k i • k j ' + k i • k j = 0, или
( ш • k i ) • k j + k i • ( ш • k j ) = 0 . Тогда (22) примет вид
П : Z = ш • ( пZ qp № ) + ( R ,pq Z qp k - k j ) • П + R ,pq Z qt kk ( ш • k p ) • k t +
+ o Spq Z rp k i k j ( ш • k q ) • k r = ш • R p„ Z qp k i k j + п№ 1 Z qp k i k j • -
-Rpp, Z qt k i k k p • ( ш • k t ) - п -jpq Z rp k i k k q • ( ш • k r ) =
= ш - ( п : Z ) + ( п : Z ) • ш т - п : ( Z • ш т ) - п : ( ш • Z ) = = ш • ( п : Z ) - ( п : Z ) • ш + п : ( Z • ш ) - п : ( ш • Z ) .
Подставляя полученное выражение в (21), с учетом (20) получаем к = ш •( п: Z) -(п: Z )• ш + п: (Z • ш)- п: (ш • Z) + п: Z, или к + к • ш - ш • к = п: (Z + Z • ш - ш • Z). (23)
Тогда окончательно соотношение запишется в скоростной форме (в ряде источников определяющее соотношение в этой форме называется гипоупругим законом):
к cr = п : Z c r ,
где верхний индекс « cr» обозначает ту или иную коротационную производную соответствующего тензора.
Далее проведем обратную процедуру — проинтегрируем в ПСК соотношение закона Гука в скоростной форме (24) и покажем его соответствие соотношению в конечной форме (20). Для этого рассмотрим коротационную производную тензорной величины а , определенной в базисе подвижной системы координат k i , которая вращается со скоростью ш :
a cr = a + a • о - о • a = — (a J k k W a • о - о • a = dt ij
= a4 kk, + a J kk, + a J kk, + a • о - о • a = ij ij ij
= a ij k k, + о • a ij kk, + a ij k k, • o T + a • о - ro • a = ij ij ij
= a ij k i k j + о • a - a • о + a • о - о • a = a J k i k j .
Полученное соотношение непосредственно следует из определения коротационной производной [3]. Тогда соотношение (24) в базисе ПСК имеет вид
• κ ij k i k j = п ijkl ζ lk k i k j ,
или o • (к jkikj) • oT = o • (п ijkl't,k kikj) • oT .
Из последнего выражения следует равенство, справедливое для любого момента времени:
κ ij k i k j = п ijkl ζ lk k i k j . (27)
Интегрируя (27), получим j ic Jk ik dт = j пiJkl Z;,k kikjdт, откуда с учетом неизменности базиса ЛСК ki в отсчетной конфигурации и компонент тензора упругих модулей в этой системе координат следует kikjj iK iJdт = ПiJkl kikjj itkdт,(28)
или, полагая отсчетную конфигурацию естественной (свободной от напряжений и деформаций),
κi kik =пi klζlkkik .(29)
Умножая последнее соотношение слева на o , а справа на o T, имеем
κi kik =пi klζlkkik ,(30)
что совпадает с соотношением в конечной форме (20). Таким образом, доказана эквивалентность упругих соотношений в конечной и скоростной формах (20) и (24) при выполнении следующих условий: компоненты тензора упругих характеристик в базисе ПСК остаются постоянными, коротационные производные мер напряжений и деформаций идентичны и определены с использованием спина, характеризующего скорость ротации введенной ПСК.
-
3. Результаты численного моделирования
Следует отметить, что рассуждения, проведенные для доказательства эквивалентности законов Гука в скоростной и конечной форме, справедливы для анизотропного случая, однако ниже в качестве примера будет рассмотрен изотропный материал (развитие работы для анизотропных материалов будет отражено в последующих публикациях авторов). В этом случае компоненты тензора п будут неизменны в любой системе координат. Тензор упругих свойств может быть представлен с использованием линейной комбинации трех изотропных тензоров четвертого ранга:
п = ас i + вс ii + ycin,(3
где с I = II = k i k1 k j k j , с II = k i k j k i k j , с III = k i Ik i = k i k j k j k i .
Тогда определяющее соотношение в скоростной форме имеет вид к cr = (ас , + вс „ + yc ,,,): Z";(32)
с применением свойств изотропных тензоров получается кcr = (ас, + вс,, + yc,,,): Zcr = а,, (Zcr)I + в(Zcr )T + yZ",(33)
где 11 (•) - первый инвариант. Поскольку рассматриваемые меры деформации и их скорости являются симметричными, последнее соотношение можно переписать в виде к cr = а,1 (Zcr) I + 2pZ cr,(34)
где введено обозначение 2р = в + Y • Соотношение Гука в конечной форме для изотропного материала будет иметь вид к = а,1 (Z) I + 2pZ.(35)
Далее в качестве мер деформационного состояния выступают тензор Альманси (6) и правый тензор Генки (7), а используемые коротационные производные в (34) – производные Зарембы–Яуманна (10), Грина–Нагхди (11) и логарифмического спина (12).
Важной характеристикой процесса деформирования является работа напряжений, которая при деформировании по замкнутому циклу для упругого материала должна быть в точности равна нулю. Известно, что локальная скорость изменения внутренней энергии u определяется только контактными взаимодействиями, является величиной, независимой от выбора системы отсчета, и определяется следующим образом [3]:
р u i = о : \7 v T , (36)
где σ – тензор напряжений Коши.
Последнее соотношение получается из закона сохранения механической энергии и уравнения движения. В случае симметричного тензора напряжений соотношение (36) можно переписать в виде р ui = о: d. (37)
Плотность на единицу массы внутренней энергии u определяется соотношением u =
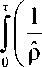
\ 1 T 1 T d dt = — j( Ja: d) dt = — J( к: d) dt, ) p о 7 p v '
где p, p - плотность в отсчетной и текущей конфигурациях; J -якобиан.
В вычислительных экспериментах задавалось движение по замкнутой траектории, а отклик материала определялся двумя способами: с использованием (34) и (35). Компоненты тензора напряжений, приведенные ниже, определены в неподвижной лабораторной системе координат (ЛСК). Согласно приведенным выше аналитическим рассуждениям напряженное состояние не должно быть отличным при применении различных форм упругого определяющего соотношения; другим вопросом является установление отсутствия диссипации энергии – в конце цикла нагружения значение внутренней энергии (38) должно равняться нулю.
Для решения тестовых задач использованы два лагранжевых закона движения по замкнутой траектории, предложенные в работе [17]:
u =
sin ( ф ) r d / h
1 + ( 1 - cos ( ф ) ) r d I h
q 2 k 1 +( 1
-
r
C0S ( ф ) ) hq 2 k 2 ,
u =
( 1 - cos ( Ф ) ) r d / h 1 + sin ( ф ) r d / h
r q 2k1 + sin (ф) -^-q 2k 2, h
где u – вектор перемещений; k i – базис неподвижной ЛСК; q i – лагранжевы координаты, фиксированные в отсчетной конфигурации; φ – угол (параметр, по которому ведется кинематическое нагружение); h – длина ребра материального прямоугольного в отсчетной конфигурации параллелепипеда с квадратом в поперечном сечении (на рис. 1 показана проекция параллелепипеда на плоскость поперечного сечения Ox 1 x 2 ), r d – второй параметр, условный радиус «окружности», по траектории которой частица совершает движение.
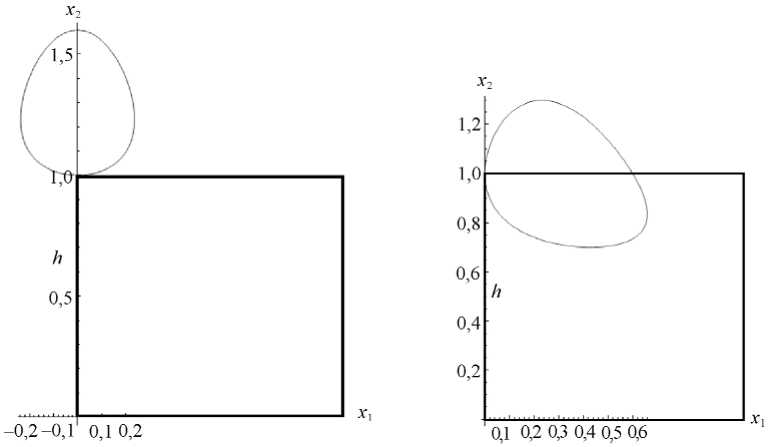
а
б
Рис. 1. Траектория движения материальной точки в плоскости Ox 1 x 2 с лагранжевыми координатами q 1 = 0, q 2 = h , при r d I h = 0,3, ф e [ 0,2п ] : а - лагранжев закон движения (39); б – лагранжев закон движения (40)
В расчетах использовались параметры материала, значения которых близки к характерным для некоторых резин: λ = 15 МПа, μ = 2 МПа, плотность в отсчетной конфигурации равнялась 1200 кг/м3; при интегрировании скоростных соотношений использовался метод Эйлера с шагом интегрирования 10–3.
На рис. 2 показана эволюция компоненты κ 12 тензора напряжений Кирхгоффа в лабораторной системе координат для нагружения (39) и (40) соответственно. Остальные компоненты не приводятся, поскольку также совпадают. Следует отметить, что на одном графике накладываются друг на друга четыре кривых, три из них – это зависимости, полученные при интегрировании в ЛСК упругого соотношения в скоростной форме и использовании коротационных производных Зарембы–Яумана, Грина–Нагхди и логарифмического спина, еще одна зависимость – результат расчетов с использованием закона Гука в конечной форме. В конце цикла значения компонент тензора напряжений обращаются в нуль с точностью до вычислительной погрешности, что является прямым следствием эквивалентности упругого закона в форме (24) определяющему соотношению в форме (20).
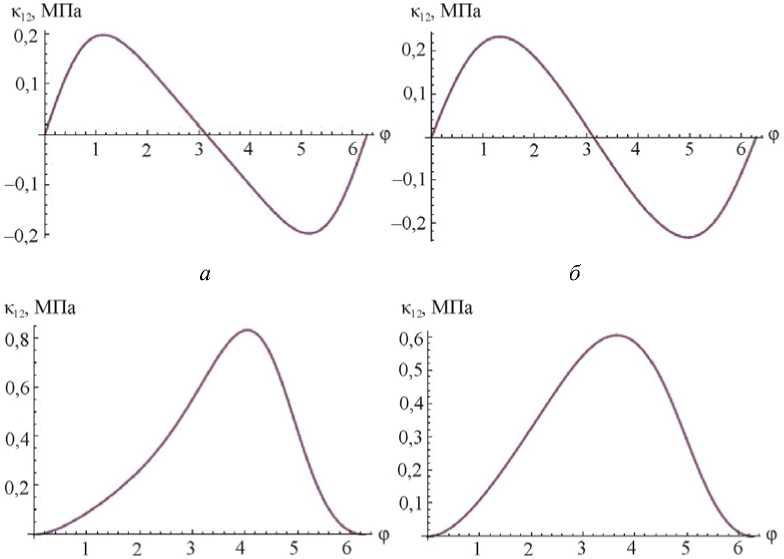
в
г
Рис. 2. Эволюция компоненты κ 12 тензора напряжений в лабораторной системе координат от параметра нагружения φ при численном интегрирования закона Гука в скоростной форме с мерой деформации тензора Альманси ( а , в ) и правым тензором Генки ( б , г ) при использовании производных Зарембы–Яумана, Грина–Нагхди, логарифмического спина, а также закона Гука в конечной форме; ( а , б ) – закон движения (39), ( в , г ) – закон движения (40)
Анализируя приведенные на рис. 2 зависимости, можно отметить близость компонент тензора напряжений (при использовании ОС с мерой Альманси, с одной стороны, с мерой Генки – с другой) в области малых градиентов перемещений и их отличие при значительных градиентах перемещений.
На рис. 3 представлена зависимость массовой плотности внутренней энергии u от параметра нагружения φ при разных мерах деформирования – Альманси и Генки.
и, кДж и, кДж
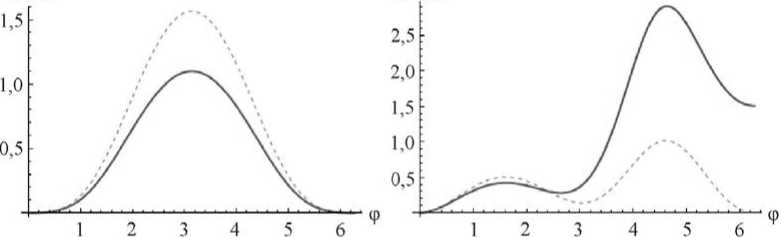
а б
Рис. 3. Эволюция массовой плотности внутренней энергии u от параметра нагружения φ: сплошная линия – мера деформаций тензора Альманси, штриховая – Генки; а – лагранжев закон движения (39); б – лагранжев закон движения (40)
Плотность внутренней энергии u определяется согласно формуле (38). Эквивалентность скоростной и конечной формы закона Гука позволяет сразу указать пару энергетически сопряженных тензоров – правый тензор Генки (его коротационная производная с логарифмическим спином равна тензору деформации скорости) и тензор Кирхгоффа. Для указанной пары тензоров при упругом деформировании работа в конце замкнутого цикла должна быть в точности нулем, что подтверждается проведенными расчетами, представленными на рис. 3. Тензоры Альманси и Кирхгоффа не являются энергетически сопряженными, поэтому внутренняя энергия, определяемая по соотношениям (37)–(38) для закона (24) (в изотропном случае – (34)), где ζ – тензор деформации Альманси, в конце цикла далека от нулевого значения (рис. 3, б).
Ключевой результат, подтверждающий аналитические выводы о соответствии соотношений в конечной и скоростной форме для изотропных упругих материалов: использование любых (численно подтверждено для 3 вариантов) коротационных производных, одинаковых и для меры напряжений, и для меры деформаций, приводит к одинаковым результатам. Если при этом используются энергетически сопряженные меры НДС, то и диссипация энергии отсутствует.
Заключение
При построении геометрически нелинейных определяющих соотношений в скоростной форме важным является вопрос выбора мер напряженно-деформированного состояния и их не зависящих от выбора системы отсчета производных. Использование вместо материальной производной (по времени) тензора напряжений его коротационной производной и тензора деформации скорости как меры скорости изменения деформированного состояния позволяет удовлетворить принципу независимости определяющего соотношения от выбора системы отсчета, однако конкретизация вида производной может быть осуществлена множеством способов. Произвольный выбор коротационной производной меры напряжений в этом случае приводит к нежелательным эффектам: осцилляциям напряжений при монотонной деформации простого сдвига (например, для производной За-рембы–Яуманна), «незамкнутости» траектории напряжений и отличию от нуля работы напряжений при замкнутой траектории деформаций. Для упругого изотропного материала в работах [15–17] показано, что использование основанной на логарифмическом спине коротационной производной позволяет избежать этих эффектов, на основании чего авторы цитируемых работ заключают, что именно логарифмический спин должен использоваться в скоростных определяющих соотношениях.
В работе установлена связь между законом Гука для анизотропного материала в скоростной и конечной формах при условиях существования подвижного материального базиса, в котором упругие характеристики тела остаются неизменными, и использования однотипных коротационных производных от мер деформаций и напряжений. Для иллюстрации проведены численные эксперименты с использованием некоторых мер деформации и их не зависящих от выбора системы отсчета производных, в том числе получаемых с применением логарифмического спина. При рассмотрении замкнутых циклов деформаций показано, что при одинаковом выборе коротационных производных для мер деформаций и напряжений в определяющем соотношении в скоростной форме, для изотропных упругих материалов при любом выборе коротационной производной выполняется замкнутость траектории напряжений, к тому же, если используемые меры напряжений и деформаций энергетически сопряжены, то наблюдается и отсутствие диссипации энергии.
Таким образом, полученные результаты свидетельствует о неоднозначности утверждения об исключительной необходимости использования логарифмического спина при формулировке геометрически нелинейных определяющих соотношений в скоростной форме. По мнению авторов, при постановке и решении задач механики твердого тела выбор мер НДС и коротационных производных должен быть обоснован с позиций физического анализа рассматриваемого процесса.
Разделы 1, 2 статьи выполнены в Пермском национальном исследовательском политехническом университете, разделы 3, 4 статьи выполнены в научно-исследовательском институте механики Нижегородского государственного университета им. Н.И. Лобачевского за счет гранта Российского научного фонда (проект № 15-19-10039).
Список литературы О геометрически нелинейных определяющих соотношениях упругого материала
- Коробейников С.Н. Нелинейное деформирование твердых тел. -Новосибирск: Изд-во СО РАН, 2000. -262 с.
- Левитас В.И. Большие упругопластические деформации материалов при высоком давлении. -Киев: Наукова думка, 1987. -232 с.
- Поздеев А.А., Трусов П.В., Няшин Ю.И. Большие упругопластические деформации: теория, алгоритмы, приложения. -М.: Наука, 1986. -232 с.
- Лурье А.И. Нелинейная теория упругости. -М.: Наука, 1980. -512 с.
- Зенкевич О. Метод конечных элементов в технике. -М.: Мир, 1975. -542 с.
- Зенкевич О., Морган К. Конечные элементы и аппроксимация. -М.: Мир, 1986. -318 с.
- Новокшанов Р.С., Роговой А.А. Эволюционные определяющие соотношения для конечных вязкоупругих деформаций//Известия РАН. Механика твердого тела. -2005. -№ 4. -С. 122-140.
- Rogovoy A.A. Formalized approach to construction of the state equations for complex media under finite deformations//Continuum Mechanics and Thermodynamics. -2012. -Vol. 24. -Р. 81-114. DOI: DOI: 10.1007/s00161-011-0220-y
- Маркин А.А., Толоконников Л.А. Меры и определяющие соотношения конечного упругопластического деформирования//Прикладные проблемы прочности и пластичности: всесоюзн. межвуз. сб. -Горький: Изд-во Горьк. ун-та, 1987. -С. 32-37.
- Truesdell C., Noll W. The non-linear field theories of mechanics. -Berlin: Springer, 1965. -602 p.
- Трусделл К. Первоначальный курс рациональной механики сплошных сред. -М.: Мир, 1975. -592 с.
- Oldroid J.G. On the formulation of reological equations of state//Proc. Roy. Soc. London A. -1950. -Vol. 200. -Р. 523-541.
- Cotter B.A., Rivlin R.S. Tensors associated with time-dependent stress//Quart. Appl. Math. -1955. -Vol. 13. -No. 2. -Р. 177-188.
- Прагер В. Введение в механику сплошных сред. -М.: Изд-во иностр. лит., 1963. -312 с.
- Xiao H., Bruhns O.T., Meyers A. Hypo-elasticity model based upon the logarithmic stress rate//J. Elasticity. -1997. -Vol. 47. -P. 51-68.
- Xiao H., Bruhns O.T., Meyers A. Logarithmic strain, logarithmic spin and logarithmic rate//Acta Mechanica. -1997. -Vol. 124. -P. 89-105.
- Meyers A., Xiao H. and Bruhns O. Elastic stress ratchetting and corotational stress rates//Technische mechanik. -2003. -Vol. 23. -P. 92-102.
- Bruhns O.T., Xiao H., Meyers A. Large simple shear and torsion problems in kinematic hardening elasto-plasticity with logarithmic rate//Int. J. of Solids and Structures. -2001. -Vol. 38. -P. 8701-8722.
- McDowell D. L. A perspective on trends in multiscale plasticity//Int. J. Plasticity. -2010. -Vol. 26. -Р. 1280-1309. DOI: 02.008 DOI: 10.1016/j.ijplas.2010
- Trusov P.V., Ashikhmin V.N., Volegov P.S., Shveykin A.I. Constitutive relations and their application to the description of microstructure evolution//Physical Mesomechanics. -2010. -Vol. 13. -Iss. 1-2. -P. 38-46.
- Trusov P.V., Shveykin A.I. Multilevel crystal plasticity models of single-and polycrystals. Statistical models//Physical Mesomechanics. -2013. -Vol. 16. -No. 1. -P. 23-33.
- Trusov P.V., Shveykin A.I. Multilevel crystal plasticity models of single-and polycrystals. Direct models//Physical Mesomechanics. -2013. -Vol. 16. -No. 2. -P. 99-124.
- Trusov P.V., Shveykin A.I., Nechaeva E.S., Volegov P.S. Multilevel models of inelastic deformation of materials and their application for description of internal structure evolution//Physical Mesomechanics. -2012. -Vol. 15. -Iss. 3-4. -P. 155-175.
- Трусов П.В., Нечаева Е.С., Швейкин А.И. Применение несимметричных мер напряженного и деформированного состояния при построении конститутивных моделей материалов//Физическая мезомеханика. -2013. -Т. 16, № 2. -С. 15-31.
- Zaremba S. Sur une forme perfectionnée de la théorie de la relaxation//Bull. Int. Acad. Sci. Cracovie. -1903. -Р. 595-614.
- Jaumann G. Geschlossenes System physikalischer und chemischer Differential-gesetze//Sitzber. Akad. Wiss. Wien, Abt. IIa. -1911. -В. 120. -S. 385-530.
- Green A. E., Naghdi P. M. A general theory of an elasto-plastic continuum//Arch. Rat. Mech. Anal. -1965. -Vol. 18. -Р. 251-281.
- Reinhardt W.D., Dubey R.N. Eulerian strain-rate as a rate of logarithmic strain//Mechanics Research Communications. -1995. -Vol. 22. -P. 165-170.
- Reinhardt W.D., Dubey R.N. Coordinate-independent representation of spins in continuum mechanics//Journal of Elasticity. -1996. -Vol. 42. -P. 133-144.


