О геометрическом параметре в уравнении интенсивности генерации дислокации

Один из возможных подходов к изучению пластической деформации кристаллических тел как целостного явления в достаточно общих условиях предложен в цикле работ Л.Е. Попова с соавторами (библиография, например, в [1-5]) Отталкиваясь от атомно-дислокационной концепции упрочнения и отдыха авторы сформулировали модели пластичности кристаллических тел, основным ядром которых является система дифференциальных уравнений эволюционного типа (уравнения баланса деформационных дефектов). Очень важно, что каждый параметр таких моделей имеет вполне определенный физический или прозрачный геометрический смысл и может быть вычислен, либо может быть указан интервал его возможных значений. Это убедительно проиллюстрировано в ряде публикаций (ссылки в [1-5]). Однако с геометрическим параметром в уравнении баланса дислокаций, которому посвящена настоящая работа, (необходимые пояснения - ниже) дело обстоит сложнее

Остановимся на самом элементарном случае: рассмотрим эволюцию только одной изолированной дислокационной петли и временно перейдем на чисто геометрический язык (длина дислокационной петли - периметр Р соответствующей замкнутой плоской кривой; площадь, заметенная дислокационной петлей, - площадь S, ограниченная кривой). Тогда плотность дислокаций р = Р, кристаллографический сдвиг a=bS, а изменение плотности дислокаций (периметра) за некоторое время At представимо в виде

Ар-АР^Г^ЦАЕ,                    (I)

где L - некоторая линейная характеристика замкнутой плоской кривой, b -модуль вектора Бюргерса, Г, - геометрический параметр, определяемый формой кривой, которая, в свою очередь, может изменяться вместе с L. Г] (L) и L таковы, что Г] (L) • L = Р (для окружности, если за L принять ее диаметр, Г ^ = тс ) Выбор L, вообще говоря, произволен и определяется соображениями удобства, но для сравнения результатов по различным классам линий вопрос о его выборе надо решить однозначно. Тем более, что иногда одним и тем же термином называют разные характеристики плоских кривых и множеств на плоскости (например, диаметр). В дальнейшем мы придерживаемся терминологии, устоявшейся в теории метрических пространств и берущей свое начало в интегральной геометрии [6] - [8]: А(<р) - ширина множества л в направлении ф (плоской замкнутой кривой - его границы) - это длина ортогональной проекции 3 на прямую, параллельную направлению ф; П = тах{Д(ф)}, ф

К-тт]А(ф)}, соответственно, диаметр и широта множества Е. В случае выпуклых ф замкнутых кривых [6]       '

Р = УА(ф)йф                               (2)

о и поэтому среднее значение ширины (Д(ф)) = Р/ л. Очевидно, что смысл последнего равенства в том, что средняя ширина множества (Д(ф)) = Ь является диаметром окружности, равновеликой по периметру границе данного множества. Именно эта величина и выбрана в качестве линейной характеристики замкнутой кривой (дислокационной петли). Для невыпуклых множеств равенство (2) надо рассматривать как приближенное

Далее,

Aa = bAS~bT2(L)LAL,                    (3)

где b - модуль вектора Бюргерса, Г2 (L) - параметр формы кривой, в общем случае отличный от ГДЬ), хотя подходящим выбором линейной характеристики L для определенного класса линий эти геометрические параметры можно сделать одинаковыми. (Для окружности, в случае выбора за L ее диаметра, Г2(Е) = л/2; если же за L принять радиус окружности, то Fi = Г2 = 2- л ) При ДЕ—> 0 комбинируя (1) и

(3), находим dp = JlP_ = _ э L

da bdS F2(L)bL        dS ’     F2(L)7

Из (4) следует, что в общем случае параметр Ф может изменяться в довольно широких пределах: от отрицательных значений, так как периметр замкнутой плоской кривой может убывать с ростом площади, ограниченной этой кривой, - до бесконечности, если принимать во внимание, что дислокация при определенных условиях имеет дробную размерность (линия фрактального типа) [17] Равенство (4) справедливо для любых дифференцируемых (кусочно-дифференцируемых) плоских кривых. Если ограничиться только выпуклыми кривыми, то оно принимает вид

Р dP

Ф = —(5) л • d S

Как (4), так и (5) практически не пригодны без каких-либо дополнительных предположений для вычисления параметра Ф в силу того, что в достаточно общих условиях неизвестна зависимость P(S) или зависимости Р и S от какого-либо вспомогательного параметра в процессе эволюции кривой. Поэтому, для получения конкретных результатов нужно либо: а) ввести дополнительные предположения;

• б)    использовать результаты имитационного моделирования процессов генерации и эволюции дислокационной петли,

• в)    возможно, что-то можно получить из принципа “длины и площади” [11, с. 354].

Приближение выпуклых самоподобных кривых

Предположим, что с изменением средней ширины замкнутой плоской кривой L она остается все время подобной самой себе - ее тип и параметры формы не изменяются (выполняется преобразование подобия, а параметр(ы) формы - инвариант этого преобразования). Тогда из (4) имеем р2

ф .=--

2л S

Таким образом, для вычисления параметра Ф имеем две формулы (4) - общие или, что тоже, (5) и (6)- справедливые только в сформулированных выше предположениях. Значение Ф, подсчитанное по (4) будем обозначать Фа1г, по (6) - Фш1. Конечно же, при выполнении предположения самоподобия Ф1п1= Фад= Ф

Таблица 1

Значения параметра Ф для некоторых классов кривых

N	Классы линий	Ф
1	Окружности	2
2	Треугольники Рельё [6] n-угольники (n=2k+l)	л/(л-Тз>2,2288 л/[л-П tg(Tr/2n)] => 2
3	Прав многоугольники	(2п/л) tg(л /п) => 2
4	Квадраты	8/л « 2,5465
5	Прямоугольники	2(1 + Х)2/( лХ)
6	Ромбы	8/(л since)
7	Параллелограммы	2(1+Х)2/(лХ sina)
8	Эллипсы	(8EW(k!)oi)
9	Эпициклоиды [7] m = 1 - кардиоиды	32(1-1/(m+2)) /л2 64/(3л2)« 2.1615
10	Гипоциклоиды [7] m = 3 - Штейнера [7] m = 4 - астроиды [7]	32(1 + 1/ (m-2)) / л2 64/л2» 6,4846 48/л2« 4,8634

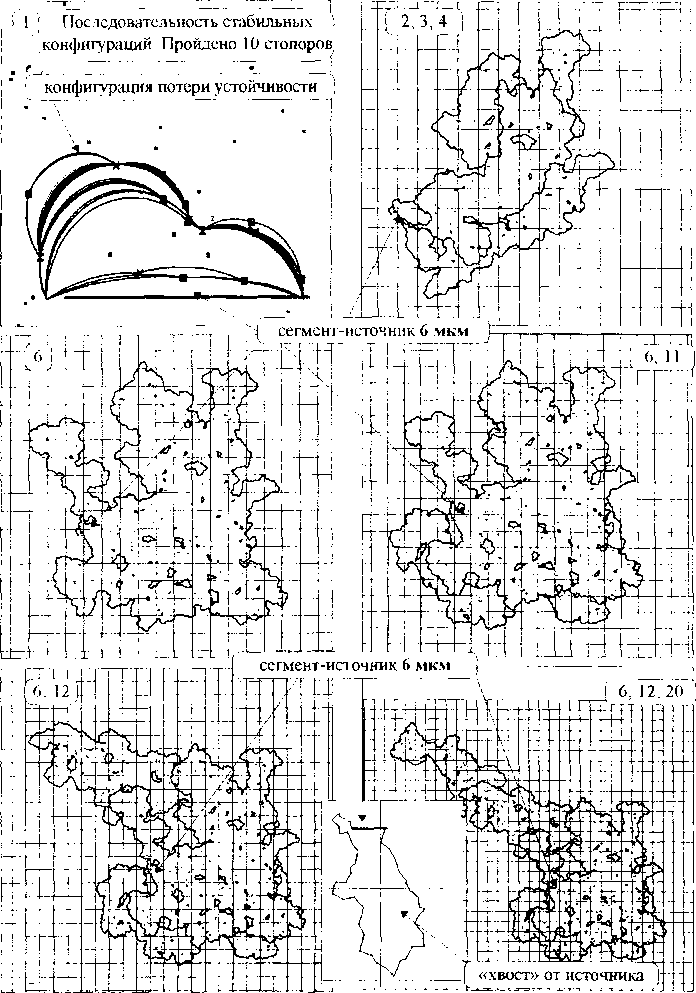
В табл. 1 представлены результаты вычислений параметра Ф по формулам (4), (6). Здесь приняты следующие обозначения: п - число сторон многоугольника (для многоугольников Рельё - нечетное), X - отношение большей стороны к меньшей для параллелограммов и прямоугольников, а - острый угол параллелограмма или ромба, с - эксцентриситет эллипса, Е(х) - полный эллиптический интеграл второго рода [18], m -модуль эпи(гипо) циклоид - отношение радиусов неподвижного и катящегося кругов [7] (в данном случае предполагается целым числом). Фигуры 1-8 выпуклые, из них 1-2 относятся к так называемым множествам постоянной ширины [6,8]. Для кривых 9-10 не выполняется предположение выпуклости, что в данном случае несущественно.

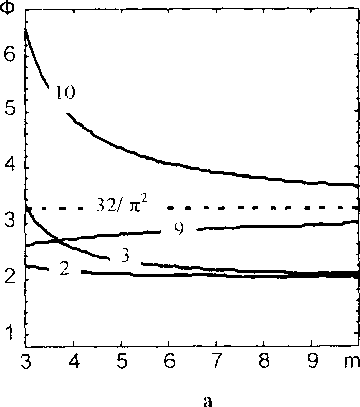
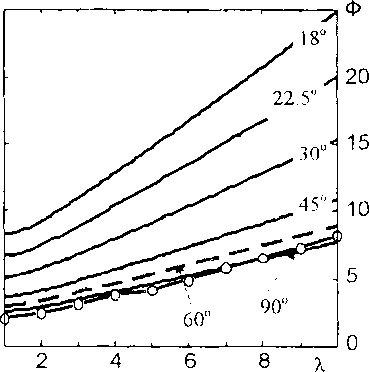
Рис 1 Зависимости геометрического параметра Ф от инвариантных относительно преобразования подобия параметров некоторых плоских фигур: а) - нумерация кривых соответствует их нумерации в табл. 1; б) - зависимости для семейства параллелограммов (квадраты, ромбы, прямоугольники) Разные кривые отвечают различным значениям а, нижняя линия с символами соответствуег семейству эллипсов с отношением полуосей X

Данные, представленные в табл.,1 и на рис.1, в комментариях не нуждаются. Отметим лишь следующее. Для эпи(гипо)циклоид с модулем m известные формулы дифференциального исчисления для периметров и площадей плоских кривых дают

Pm= 8R(l±l/m) , Sm= лР2(1±1/ т)(1±2/т).

Переходя к пределу при фиксированном R (радиусе неподвижного круга), имеем Lim Pm=8R, LimSln = nR2. В этом предельном случае эпи(гипо)циклоиды т->со          т->оо

«стремятся» к окружности радиуса R Но длина этой «окружности» 8R (вместо 2nR), а площадь, ограниченная ею, как и для обычной окружности - kR². Видимо здесь имеет место промежуточный вариант между классическими и «береговыми» [17] линиями.

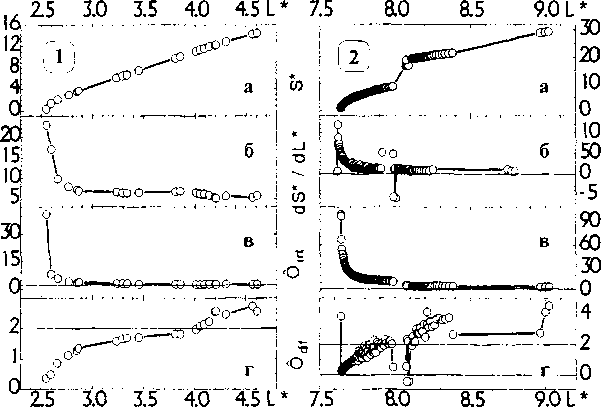
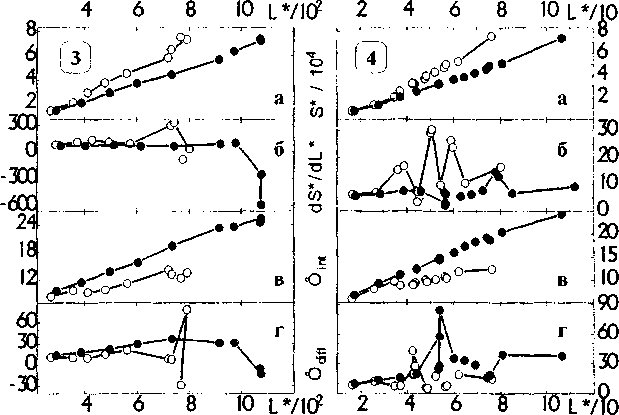
Конечно же, табл 1 можно продолжить. Но даже, если ограничиться только алгебраическими кривыми, то, как известно, кривых второго порядка 4, третьего -1875, четвертого - 84551... [7]. Поэтому крайне необходимо иметь общие, не зависящие от класса кривых, оценки геометрического параметра Ф. Так как Ф может принимать отрицательные значения и стремиться к бесконечности, то общих двухсторонних неравенств для Ф (без каких-либо ограничений на кривые), по-видимому, предложить нельзя. Поэтому не случайно, что в классической монографии по неравенствам [9] и в методах, развиваемых в [10], нет результатов, непосредственно применимых к подобным оценкам. Но если ввести какие-либо ограничения на форму кривых, скажем, в виде определенной комбинации их широты К и диаметра D , то из классических неравенств интегральной геометрии [6,8]

Р² >4л5 , V3S>K² ,P>kK,2S>KD,

P>2(D2 -К2)1/2 + 2Karcsin(K/D), P<2(D2 -К2)1/2 + 2Darcsin(K/D), 2S

можно получить достаточно точные двухсторонние оценки параметра Ф Ограничения на форму кривых, конечно же, должны соответствовать конкретному содержанию рассматриваемой физической задачи (анизотропия, специфика барьеров, различия в краевых и винтовых дислокациях...). К сожалению, полная система неравенств остается пока (1983г.) неизвестной. “Нахождение для каждого из неравенств множеств, для которых выполняется равенство, - очень трудная математическая задача”[6].

Оценки геометрического параметра Ф по результатам имитационного моделирования эволюции дислокационной петли в поле случайно расположенных точечных препятствий

При имитации на ЭВМ генерации и эволюции дислокационной петли [12, 14 -16, 19] в плоскости кристаллографического скольжения, содержащей точечные [13] случайно распределенные препятствия, в определенные промежутки времени, кроме всего прочего, регистрируются периметр дислокационной петли и её площадь (площадь, по которой прошел кристаллографический сдвиг). Эти данные позволяют проследить за геометрическим параметром Ф для эволюционирующей по своим законам (а не в предположении самоподобия) дислокационной петли. При этом имеется возможность вычислять как Ф^г, так и Ф^ и тем самым судить о том, как сильно влияет невыполнение предположения самоподобия на приближенный подсчет параметра Ф

В работе [14] рассматривалось термоактивируемое расширение дислокационной петли в плоскости кристаллографического скольжения со случайно распределенными однотипными препятствиями малой прочности под действием приложенного напряжения. Отмечалось, что в стабильных конфигурациях дислокационные петли по форме близки к окружностям, то есть можно считать, что предположение самоподобия выполняется. Вычисленные значения геометрического параметра Ф (как по формуле (4) так и по (6)) изменяются незначительно: от 2,0 до 2,81, 2,0 - 2,85, 2,0 - 2,64 в разных ЭВМ-экспериментах. При этом средняя ширина дислокационных петель изменялась в первом эксперименте от 28,4 до 101,8 , во втором - 71,7 - 121,2 и от 101,4 до 146,2 средних расстояний между ближайшими стопорами - в третьем Зависимости Ф от L не являются монотонными.

Значение Ф , вычисленное по результатам работы [15] по формуле (6) для конфигурации, когда дислокационная петля отшнуровывается от источника Франка -Рида, составило 2,21, что сопоставимо со значением Ф для кардиоиды (см. табл. 1).

Иная ситуация в случае эволюции дислокационной петли от источника Франка -Рида, когда в плоскости залегания источника присутствует спектр препятствий с существенно различными прочностями и среди них есть атермические препятствия [16]. Ряд последовательных конфигураций дислокационной петли в этом случае представлен на рис.2.

Рис. 2 . Эволюция дислокационной петли от источника длиной 6 /, под действием внешнего напряжения т* Номера в углах рисунков соответствуют номерам дислокационных конфигурации из табл.2. В квадрате сетки каждого рисунка в среднем по 225 стопоров

Препятствия в плоскости кристаллографического скольжения, за исключением первого блока, в котором представлена эволюция дислокационного сегмента до конфигурации потери устойчивости - конфигурации, после которой все процессы происходят в над барьерном режиме (сегмент теряет устойчивость), не изображены, их в каждом из представленных фрагментов - более 200 тысяч.. Замкнутые маленькие кривые (часть из них на рисунке выглядит жирными точками) - «острова» незавершенного кристаллографического сдвига [19], оставшиеся за фронтом скользящей дислокации и представляющие собой труднопреодолимые участки плоскости кристаллографического скольжения, которые дислокация обходит по механизму Орована. Конфигурация 11 - дислокационная конфигурация в момент замыкания сегмента-источника в дислокационную петлю (момент срабатывания источника). Вставка в нижней части рисунка («хвост» от источника) - конфигурация, оставшаяся после отшнуровывания дислокационной петли. Его «геометрия» существенно влияет на генерацию источником последующих петель, вплоть до запирания источника. Количественная информация о дислокационных конфигурациях, частично представленных на рис.2, сведена в табл. 2

Таблица 2

Некоторые характеристики дислокационных петель, представленных на рис. 2

№	Число узлов	Периметры		Площади		Пройдено стопоров
		PL*	РО*	SL*	SO*	всего	перереза ние.м	по мех. Орована
1	3	4	5	6	7	9	11	17
2	70	90,9	4,19	365,3	0,32	315	301	14
3	586	652,8	158,53	7570,1	140,49	6893	6452	441
4	906	992,6	428,03	16070,7	365,19	14963	13902	1061
5	1412	1566,8	699,79	25153,5	570,00	23609	21924	1685
6	1487	1680,5	791,48	27387,6	649,39	25732	23869	1863
10	1520	1715,1	1126,02	33326,8	1061,46	32324	28885	3439
11*	1473	1655,3	1209,47	33772,6	1262,84	32630	29110	3520
12	1563	1768,9	1908,32	44685,4	2905,74	41782	37238	4544
20	2045	2279,4	2048,84	52024,2	2961,56	50205	43681	6524
21	2542	2830,0	2208,18	59337,4	3028,89	57201	50263	6938

В табл.2 в колонке «число узлов» приведено число стопоров, с которыми в данный момент времени контактирует дислокационная петля, где PL* и РО* -периметры петли и всех островов незавершенного кристаллографического сдвига в данной конфигурации в единицах среднего расстояния между ближайшими стопорами в плоскости кристаллографического скольжения ls ; SL* и SO* - площади, охватываемые дислокационной петлей и островами незавершенного кристаллографического сдвига в единицах (ls)2

Уже простой взгляд на рис.2 убеждает, что предположение самоподобия эволюционирующей дислокационной петли существенно нарушено и формулу (6) для вычисления геометрического параметра использовать, вообще говоря, нельзя. Это же следует и из данных, представленных на рис.3, на котором, в целях сравнения результатов, все же приведены значения ФШ1

Рис.З. Зависимости геометрических характеристик дислокационных конфигураций от средней ширины дислокационной петли (пояснения в тексте)

Зависимости (а) непосредственно регистрируются в машинных экспериментах, (б) - результаты численного дифференцирования кривых (а). В первом и во втором (разница в длинах источников - 4 ls и 12 ls соответственно) блоках - результаты по «до критическим» конфигурациям (блок 1 на рис.2). Зависимости, представленные в третьем и четвертом блоках рисунка, построены по конфигурациям дислокационных петель от соответствующих источников Их в каждой ячейке по две - «короткие» кривые (незаполненные символы) и «длинные» (темные кружочки). Первые из них построены без учета островов незавершенного кристаллографического сдвига, при построении вторых в периметр дислокационной петли включены их периметры, а из площадей, ограниченных дислокационной петлей, вычтены площади островов (в этих областях не прошел кристаллографический сдвиг). Как и следовало ожидать, значительна разница между Ф^р и ФшГ Встречаются конфигурации с отрицательными значениями геометрического параметра; они как раз приходятся на те моменты, когда в результате эволюции дислокационной петли у нее сокращается периметр при некотором возрастании площади (петля «округляется»).

Заключение

Конечно же, усреднение по достаточно представительной группе дислокационных петель значительно сгладит различие теоретических и ЭВМ-экспериментальных оценок рассматриваемого в статье геометрического параметра Кроме того, при количественном описании интенсивности генерации дислокаций в процессе пластической деформации необходимо учитывать и длительность деформирующего воздействия; в простейшем варианте хотя бы два предельных случая: 1) когда время деформирующего воздействия меньше времени элементарного акта кристаллографического сдвига - формирования одной дислокационной петли (импульсное нагружение), 2) когда время деформирующего воздействия превышает время образования дислокационной петли и даже время формирования зоны сдвига, то есть время формирования всей серии дислокационных петель, испускаемых источником до его остановки (статический случай). После этого реально подняться на следующий структурный уровень в описании пластической деформации - зону сдвига. Но это предмет последующих исследований и публикаций