О гипергеометрическом подходе к решению алгебраических уравнений

Рассмотрим общее алгебраическое уравнение:

zⁿ + x 1 zⁿ^ + ... + x_pz^np - 1 — 0, n> n 1 ... > n_p 0.

В 1921 г. шведский математик Меллин предъявил интегральную формулу [Mellin, 1921], а также разложение в гипергеометрический ряд для решения z(x) — z(x 1 ,...x_p) рассматриваемого уравнения (см. также [Семушева, Цих, 2000]). Им было найдено решение для ветви с условием z 0 ( 0 ) — 1, которое называется главным решением. Нетрудно проверить, что все остальные решения уравнения (1) получаются из главного по формуле:

z j (x) — s^jz(sⁱⁿ 1 x 1 ,...,s^Jnpx_p),j — 1,... ,n - 1,

2ππ где s — e n - первообразные корни из единицы степени n.

В статье [Семушева, Цих, 2000] на основе интегрального представления Мел-лина и теории многомерных вычетов был вычислен ряд Тейлора и описана его область сходимости для главного решения уравнения (1). Этот ряд следующий:

( - 1 fr

^ n n

V ^x 1 k 1

1 - n 1

где n i —n - n i , | k | — k 1 + . + k_p , Г(к) - гамма функция Эйлера.

^ n n

В данной работе рассматривается уравнение (1) при p - 1 . В этом случае (1) содержит лишь один параметр и имеет вид:

z^Il+xz^m - 1 = 0                                              (3)

(здесь x и m обозначают соответственно x 1 и п 1 ).

В статье будет получена формула для решения (3) в классе гипергеометрических функций вида:

„ Fn -i (ai, • •, an; в, • •, вп -1; y(x» , где y(x) - функция, линейно зависящая от параметра x. Напомним, что обобщенной гипергеометрической функцией nFn-1 (а1, —, ап; в1, —, вп-1 ‘Л) называется ряд:

n ^F n -1 ^(а 1 ’ •

то

•, ап ’ в1 , — • , вп-1 ’О — Е к-0

^(а 1 ) k • — • ^(a n )_k

(в 1 ) k • — • (в п - 1 ) k k!

t k ,

где (а ) _h

Г(а + к) Г(а)

символ Похгаммера.

Теорема . Главное решение z 0 (x) уравнения (3) допускает представление в виде суммы обобщенных гипергеометрических рядов:

п - 1

z 0 (x) = -  £ п s=0

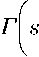
1 + ms

п

s! Г 1 -

1 + ms

п

xs

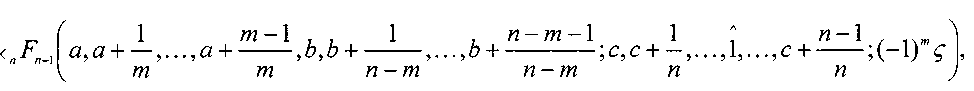
c = c(s) = - +1, п п a = a(s) = — + —, b = b(s) = — - —-----, п mn п п(п - m)

где

и применим к нему формулу дополнения:

1 _ r(z) sin nz

Г( 1 - z)

.

π

1 ”

z 0 (x)- Е п к- 0

( - 1 )^к Г | ¹ + mk | ________ I п п )

< 1 п - m к! г I---к +1

I п п

x

к

Тогда получим, что

Г ^f 1 + mk j г I

_ /        1 V n n J ¹

z 0 (x) =X —-------- nn k=0

1 +n n n k!

m , V J 1 , mk )

— k I sin n I + I

J     V n    n J ь

----------------- x

.

Далее воспользуемся формулой Гаусса–Лежандра для гамма-функции [Бейтмен, Эрдейн, 1973], которую запишем в следующем виде:

m -1 ( _r A

ПГ |z + r| Т-1/ \ _   r=0 V m J m — 2,3,4,....

r(mz)   -----1-------1---- ,

—(m -1 ) — mz

( 2n ) ²     m ²

Согласно ей, множители, стоящие в (8), будут такими:

k!- Г n I - + 1

V V n n

¹ (n - 1 )  - ¹ - k

( 2n ) ² n ²

n ^-1 f Ъ 1 F A П Г | ^k + ¹ + - |, r= 0 V n n n J

Г ^{f 1} + m^ I - г m ^k +

mk

n n

V V n mn

¹ (m - 1 )

( 2n ) ²     m

mk n

m —1 f "I Fi

П Г I ^k + — + r 1 | ,

_Г 1 = 0 V n mn m J

Г I ^-

m , — k

n

n J         1 (n - m - 1 )         1 + 1 - k-^m

( 2n ) ²       (n - m) ^{2 n n}

П r|k - r2=0 V n n(n - m)

n - m - 1

+ — n

r 2

.

- m

Подставляя полученные выражения в (8) и очевидные действия, перепишем (8) в виде:

выполняя некоторые достаточно

z 0 (x) - -

n n ² m

1 1

----x

11 +-

^{2 -}(n - m) ^{2 -}

m - 1 i 1,     1      r A n - m - 1 / Ь

П Г I ^k + — + ^r П Г I ^k -

” _r = о ^ n mn m)_r =o —п n(n - m)

x X ^{1                   2}

k- 0

+ —

n

^r 2

где g -

m^m(n - m)ⁿ - ^m

nn

n — 1

П г | ^k + 1 + - r= 0 V n n n_

— I k m ^ n • _f 1 , mk) ---C n Sinn — +   ,

V n n J

xⁿ . Заметим, что в полученном представлении решения z 0 (x)

z 0 (x)-

3 11      11

-- _              _+—

V nn ² m ^{2 n} (n - m) ^{2 n}

x

m - 1                          n - m - 1

s  П г I - + — + r1 +1 |n г |  --1— + - n-1   ^ n mn m n n(n - m) n n у r1 0 vy '2 0 v_______ c Е                 - s-0   l-0                  п г \ - +1 + - + l | r-0 (n n n J

r 2

^^^^^^B

— + l I m A -  (1 ms    .I c sinnI   ++ ml I.

I n n J

Далее, следуя представлению обобщенного гипергеометрического ряда, представим внутренний ряд в виде (4), для этого воспользуемся ранее упомянутой формулой Гаусса – Лежандра:

m - 1                                  ¹ (m -1 )

П г | ^- + — + —I -( 2n ) ² ' )

- 1 = о ( n mn m J

m

1 ms 1

2 n n

г | ms ₊ 1 ( n n

11 n - m 1 n ^- m - 1                                                   (n - m - 1 )            - -+

П г I-- ¹ + ^M = ( 2n ) ² ' ) (n - m) ² n n г I n-^s - ¹

r2=0 (n n(n - m) n - m J                             ^ n n n -1                                1 (n-1) -i-s

Пг|s + 1 + -| -(2n)2   n 2 г(s +1), r=о < n n n J

1 , ms I 1 , ms а также тем, что sinnI — + — + ml I = (-1) sinnI — + — n n

n n

В результате решение z 0 (x) уравнения (3) представится следующим образом:

ms , 1 1 „| n - m   1

— + I г I-----s n n J ^ n n s!

s - ( ms 1 x Sin n I   + —

I n n

x

n - 1

z 0 (x) = -    Е nns=0

x

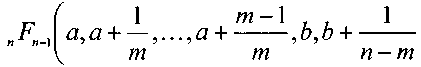
,  n-m-\      1 _Л b +---------; с, c + —,..., 1

n-m     n

и — 1          I

^;(-1)Ч L

и            )

где значения a = a(s), b = b(s), c = c(s) находятся согласно (6). После применения ms 1 I I ms 1 I - формулы дополнения к произведению г| — + — |sinn| — + — I, убеждаемся в < n n J    < n n J справедливости (5).

Каждый из полученных рядов сходится при | c(x) |< 1 (см., например, [Бейтмен,

Эрдейи, 1973]), а это в силу (7) и означает, что найденные ряды сходятся в круге i i              nn

|x|<----------- mm(n - m)n-m

Отметим, что все точки дискриминантного множества уравнения (3) лежат на граничной окружности

nn

|x|- mm(n - m)n-m

найденного круга сходимости ря-

дов [Михалкин, 2006].