О глобальных свойствах уточнённого порядка

Уточнённый порядок играет важную роль в теории роста субгармонических функции, в ряде других разделов математики.

Абсолютно непрерывная функция р ( r ) на полуоси ( 0 ,” ) называется уточнённым порядком в смысле Валирона, если выполняются следующие два условия :

• 1)    существует предел l™ ^{р ( r} ) = ^{р (} ” ) = ^{р е (} - ”, ⁺ ” ) ^{, (1} )

• 2)    lim r ln гр ( r ) = 0. ( 2 ) r→ ∞

В приложениях чаще всего используется не сам уточнённый порядок р ( r ) , а функция V ( r ) = r^{p ( r} ) . Отметим следующее свойство уточнённого порядка.

Отметим следующее свойство уточнённым порядком (см., пример [1])

Теорема 1. Для любого t >0 существует предел lim r→ ∞

V ^{( tr} ) V ( r )

= t^p, ( 3 )

и этот предел равномерный на любом сегменте [ a,b ⁽ 0 <^х ).

Если р (r) - уточнённый порядок, то существует дифференцируемый, и даже аналитический, уточнённый порядок р 1 (r) такой, что lim r → ∞

V ^{( r} )

V 1 ( r ) ¹

где V 1 ( r ) = г^{р 1 ( r} ).

Поэтому предположение о дифференцируемости уточнённого порядка часто не ограничивает общности рассуждений. В дальнейшем мы будем предполагать, что функция р ( r ) является непрерывно дифференцируемой на полуоси ( 0 ,” ) .

Далее будет исследована функция , о которой уже говорилось в анатоции. Терема 2. Пусть р ( r ) - нулевой уточнённый порядок ( р ( r ) ^ 0 ,r ^ ^ ), удовлетворяющий условию р ( r ) = ^- р ^{( r} ) и пусть

V ( rt )              V ( rt )

у ⁽ t ) = r >  ⁰         ,у ⁽ t ) = inf        .

V ( r )            r > 0 V ( r )

Тогда справеднливы следующие утверждения:

• 1)    у ⁽ t ) ,у ⁽ t ^{)e (0} ;^ro ) ;

• 2)    у ⁽ t ) > у ⁽ t ) ,у ⁽1 ) = у ⁽1 ) = 1 ;

• ^{3)    у ( 1} ) = ? 1 t ) ;

• 4)    у ( t 1 t 2 ) ^у ( t 1 ) у ( t 2 ) ,у ( t 1 t 2 ) ^Y ( t 1 ) у ( t 2 ) ;

• 5)    у ( t ) >V ( t ) ,у ( t ) ( t ) ;

• 6)    Функции у ( t ) и у ( t ) являются непрерывными функциями на полуоси ( 0 ,” ) .

Обычно уточнённый порядок р (r) применяют для исследования асимптотического поведения функцийf(r) по направлению r .-х. В этом случае поведение функциир (r) в окрестности нуля не играет никакой роли. Однако, в некоторых вопросах поведение Р (r) в окрестности нуля также важно. Удобным, является условие: р (r) удовлетворяет равенству р (r-)--р(r), или, что то же самое, V(r)-V(1). Принятие таких ограничений позволяет доказать следующую теорему.

Теорема 2. Пусть р (r) - нулевой уточнённый порядок (р (r) ^ 0,r ^ да), удовлетворяющий условию р (1)--р(r) и пусть у (t)=r>0

V ( rt )

V ⁽ r ) '

Тогда у (t) - непрерывная функция на полуоси (0,”) и выполняются соотношения limJnriti- о, limJniW-0.

t ^ да In t         t ^ + 0       1

ln

t

Отметим, что в случае если р ( r ) - р+р ( r ) , где уточнённый порядок р ( r )

удовлетворяет условию теоремы 1 получаем глобальное неравенство

• V ⁽ rt ) ру ⁽ t ) V ⁽ r ) , ⁽ r ,t ) е ⁽0 ,го ) . ( 5 )

Использование этого неравенства позволяет упростить доказательство ряда известных утверждений.

Теорема 3. Пусть – произвольный уточнённый порядок, – множество из единичной сферы, пусть

А >0

о

. Тогда, если при

выполняется неравен-ство

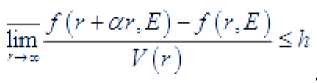
то равномерно на сегменте

выполняется неравенство

— /(>+^:£)-/(>=£)

JR

1Ш1---------—--------

Последнее означает, что функция

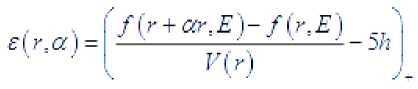
стремится к нулю при

Равномерно на сегменте

Доказательство. Обозначим /(г) = 7(л₌£) , r - s'

. В новых обозначениях неравенство (4.13) выглядит так

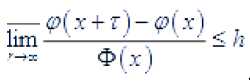
[-ln2Jn(l + 2d)]

Если утверждение теоремы неверно, то существуют последовательность

и посл-едовательность и

такие, что выполняется

неравенство

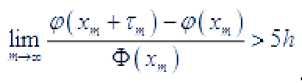
. Обозначим

5e(0=min(ln2:ln(l + 25)-lnd))) Пусть

– возрастающая последовательность измеримых множеств. Из неравенства

(4.14) следует, что -:-L

Далее обозначим

hm mes£„ = J

. Поэтому ™-z

F„ = {/? € [-J, to (1 + Ь)]: ф (x_t + r_t)- a>( x_s + r_t - p ) < 2ЛФ (x_t + r_t - p) 3 k >  m}

– также возрастающая последовательность измеримых множеств. Из

Uf« =[-^ to(l+b)]

неравенства (4.14) следует, что                     . Поэтому ton mesF„ = to (1 + b) + о

• 5. e | 0₇: 8 I T rxrnn

Пусть         . Тогда существует число такое, что при будут выпо-лняться неравенства

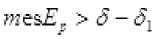
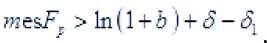
Обозначим

^=M-f;

(арифметическая разность множеств)

Справедливы вклю-чения

Оба множества

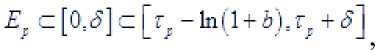
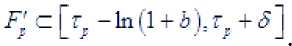
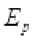
и являются частью сегмента

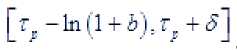
Сумма мер этих множеств больше длины указанного сегмента. Поэтому пересечение этих множеств не пусто. Пусть          . Тогда         , где

PeF,

. Поэтому выполняются нерав-енства

^(x, + «)-$>(x, ) < 1ИФ^х_р )

p(x, +5) -^(r^ + r, - ^ ) < 2ЙФ(х^ + г, - з )

Складывая эти неравенства, и учитывая равенство               , получим

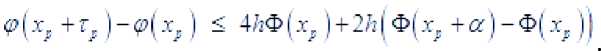
. Далее находим

Обозначим

Ф ( х_? + а )- Ф ( х, ) г( е\ ) - Г( г_; )

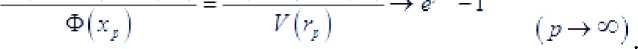
Так как ае (0,J), то при достаточно малых ^ и достаточно больших -:' будет +5      )<5йФ(^ )

выполнять-ся неравенство                        . Это противоречит (6).

Теорема доказана.

1 R         G           ^([r^jx£)

В леммах 1, где встречается функция           , она определяется различным образом. Сейчас мы сформулируем условия, обеспечивающие lim ^((r^lx-ff)

существование предела Р--^:         . При выполнении этих условий функции, которые в леммах 1 обозначены одним символом совпадают.