О характере математической некорректности обратной задачи эллипсометрии для сверхтонких поверхностных пленок
Автор: Бобро В.В., Семененко А.И.
Журнал: Научное приборостроение @nauchnoe-priborostroenie
Рубрика: Оригинальные статьи
Статья в выпуске: 4 т.10, 2000 года.
Бесплатный доступ
В работе изучен характер математической некорректности обратной задачи эллипсометрии для сверхтонких (менее 10 нанометров) прозрачных поверхностных пленок на однородной подложке. Показано, что математическая некорректность в этом случае обусловлена не только экспериментальными ошибками в измерении поляризационных углов, но также и неадекватным выбором модели отражающей среды, проявляющимся в неточном задании параметров подложки, считающихся известными, и в пренебрежении даже очень тонким (порядка 0.1 нанометра) переходным слоем на границе между пленкой и подложкой. Эти выводы носят не только качественный характер, они подтверждены как реальным, так и численным экспериментом, проведенным с помощью специальной математической программы.
Короткий адрес: https://sciup.org/14264150
IDR: 14264150 | УДК: 535.5:
Текст научной статьи О характере математической некорректности обратной задачи эллипсометрии для сверхтонких поверхностных пленок
Реализация предельных возможностей метода эллипсометрии обеспечивается не только повышением точности измерения поляризационных углов Ψ и Δ, но существенно зависит и от надежности методов интерпретации экспериментальных результатов. Речь идет прежде всего о методах решения обратной задачи эллипсометрии. Это очень сложная проблема.
Существенные трудности в решении обратной задачи эллипсометрии проявляются прежде всего при попытке определения параметров сверхтонких (менее 10 нм) прозрачных поверхностных пленок на однородной подложке. Эта задача для прозрачных пленок достаточной толщины является тривиальной и может быть решена (при известных оптических константах подложки) с помощью номограммы [1]. Однако при переходе к сверхтонким прозрачным пленкам ситуация резко меняется. Параметры таких пленок исключительно неустойчивы относительно экспериментальных ошибок поляризационных углов Ψ и Δ. Даже небольшие ошибки (порядка 1 минуты) в измерении этих углов при обычном подходе к решению обратной задачи приводят к совершенно нереальным значениям параметров пленки [2].
НЕУСТОЙЧИВОСТЬ РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ НА СВЕРХТОНКИХ ПЛЕНКАХ
Это можно понять, проанализировав номограмму для системы подложка—прозрачная однородная пленка, построенную на координатной плоскости (Ψ, Δ). Каждому циклу номограммы отвечает конкретное значение показателя прелом- ления пленки, толщина же пленки изменяется вдоль цикла. Для определенности рассмотрим номограмму рис. 1 для случая, когда подложкой является кремний (см., например, [1]). Циклы номограммы сходятся в начальной точке О, и их расположение относительно осей Ψ и Δ таково, что наблюдается сверхчувствительность показателя преломления пленки n относительно очень слабого изменения поляризационного угла Ψ (см. рис. 1). Если экспериментальная ошибка сдвигает Ψ в сторону меньших значений (влево по номограмме), то это резко увеличивает значение n. Например, для сверхтонкой пленки SiO2 показатель преломления может достигать совершенно нереального для SiO2 значения = 3.2 и даже больше, в то время как толщина d относительно стабильна. Если же экспериментальная ошибка сдвигает угол Ψ в сторону бóльших значений (вправо по номограмме), то в этом случае ситуация более сложная. Показатель преломления по-прежнему совершает бросок, но к значению n = 1, достигая также совершенно нереальной величины = 1.01. Что касается толщины пленки, то ее поведение определяется следующим обстоятельством.
Для прозрачной пленки наблюдается периодичность циклов по толщине [1] с величиной периода d 0 = 11 X - ! ■ (1) 2-^ n - n0 sin ф0
где X — длина световой волны; n 0 — показатель преломления внешней среды; ф 0 — угол падения светового пучка.
При n ^ 1 изменение периода d 0 не носит принципиального характера, но сам цикл в этом
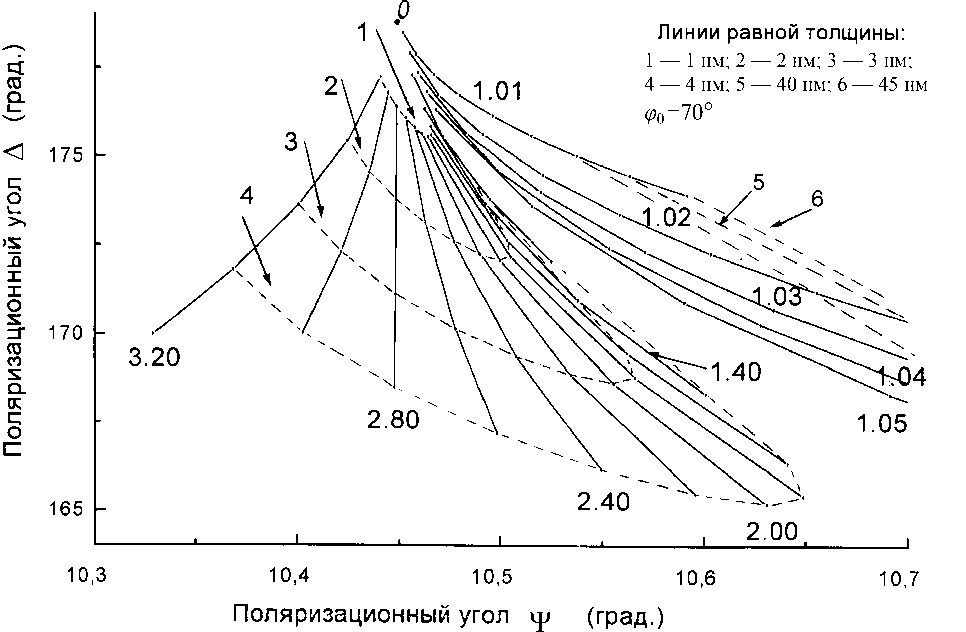
Рис. 1. Номограмма для системы кремний—прозрачная однородная пленка
случае, как видно из рис. 1, в пределе стягивается к начальной точке О, т.е. при n ^ 1 интервал толщин (0, d 0 ) распределяется по циклу с возрастающей плотностью. Иначе говоря, линии равной толщины на номограмме, отвечающие значениям d = 5, 10, 15, 20, 25 и более нанометров, в местах их пересечения с циклами, которым соответствуют значения n , близкие к единице, приближаются к точке О . А это означает, что при сдвиге Ψ вправо не только показатель преломления n ^ 1, но и толщина d сверхтонкой пленки ( d < 5 нм) увеличивается во много раз, достигая значений 30– 35 нанометров.
ИНТЕРПРЕТАЦИЯ НЕУСТОЙЧИВОСТИ, УТОЧНЕНИЕ КЛАССИЧЕСКОЙ МОДЕЛИ
Таким образом, пытаясь определить параметры d и n сверхтонкой прозрачной пленки, используя классический подход, мы попадем в область абсолютной нефизичности. Это и есть проявление истинной математической некорректности. Возможна также ситуация, когда задача по определению двух параметров на одном угле падения, несмотря на полную определенность математической проблемы (в том смысле, что число неизвестных параметров равно числу уравнений), из-за экспериментальных ошибок не имеет решения. Это тоже является проявлением истинной некорректности [3].
К математической некорректности при решении обратной задачи для сверхтонких пленок может приводить и неточный выбор модели отражающей среды, проявляющийся в неточном задании параметров подложки ( n s , k s ), считающихся известными, и в пренебрежении даже очень тонким (порядка 0.1 нм) переходным слоем на границе между пленкой и подложкой. В этом случае экспериментальная точка (Ψ э , Δ э ), которую в рассматриваемой ситуации целесообразно считать точно заданной, заметно сдвигается (влево или вправо) относительно начальной части упрощенной номограммы, отвечающей идеальному случаю (переходный слой отсутствует, а параметры подложки заданы точно). Это ясно прослеживается на рис. 2.
Предположим сначала, что параметры подложки заданы точно, а переходный слой, толщина di которого удовлетворяет условию di << d, (2)
существует, но игнорируется. Если этот слой оптически менее плотен по сравнению с пленкой, то начальная часть цикла, отвечающая переходному слою и исходящая из точки О (чистая однородная подложка), будет более пологой по сравнению со следующей частью цикла, начинающейся в точке
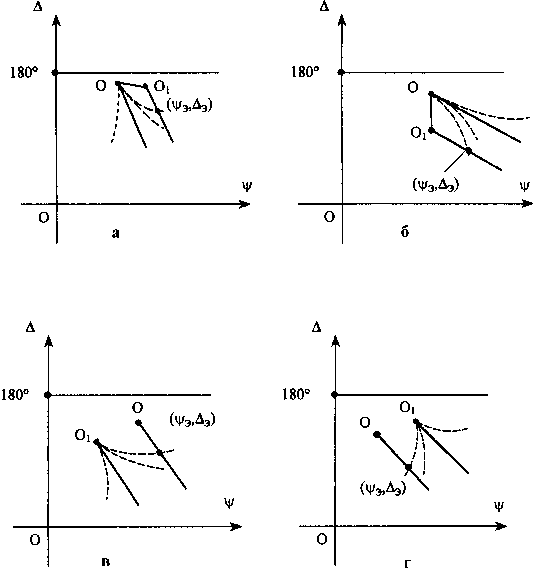
Рис. 2. Графическая оценка ошибок в определении d и n , обусловленная пренебрежением переходным слоем и неточным заданием расчетных значений оптических постоянных подложки: а, б — переходный слой игнорируется, подложка задана точно; в, г — переходный слой отсутствует, параметры подложки заданы неточно
0 1 и отвечающей конкретной однородной пленке. В случае пренебрежения переходным слоем ( d i = 0) циклы для пленки начинаются уже в точке О , образуя упрощенную номограмму. Как видно из рисунка 2, а это обеспечивает сдвиг экспериментальной точки (Т э , А э ) относительно упрощенной (идеальной) номограммы для пленки вправо, что приводит к n ^ 1 и резкому увеличению расчетной толщины пленки. Если же переходный слой оптически более плотен по сравнению с пленкой, то возникает ситуация, изображенная на рисунке 2, б. Здесь экспериментальная точка (Т э , А э ) относительно упрощенной номограммы для пленки сдвигается уже влево, что приводит к существенному росту показателя преломления и не столь значительному изменению толщины пленки.
Рассмотрим теперь другую ситуацию, когда переходный слой отсутствует, а параметры подложки заданы неточно. Известно [1], что начальной точке О номограммы в случае прозрачной подложки отвечает значение А = 180 ° , а в случае поглощающей — А < 180 ° , при этом с ростом коэффициента поглощения начальная точка сдвигается вниз и наоборот.
Что касается показателя преломления, то при его уменьшении значение Т в начальной точке уменьшается (при весьма незначительном уменьшении угла А) и наоборот. Будем обозначать начальную точку, отвечающую подложке с истинными значениями оптических констант, через О , а начальную точку, отвечающую подложке с приближенными (расчетными) значениями оптических констант, — через О 1. Из предыдущего ясно, что может иметь место любое относительное расположение точек О и О 1 , а это означает, что экспериментальная точка (Т э , А э ), в принципе, может быть сдвинута как вправо (см. рис. 2, в), так и влево (см. рис. 2, г) относительно исходящей из точки О 1 номограммы для пленки, что приводит к описанным выше результатам.
ЧИСЛОВОЕ МОДЕЛИРОВАНИЕ ЭФФЕКТА ВОЗНИКНОВЕНИЯ ПОГРЕШНОСТЕЙ
ДЛЯ СВЕРХТОНКИХ ПЛЕНОК
Для количественного подтверждения путем проведения численного эксперимента полученных здесь качественных результатов была создана специальная математическая программа, смысл которой сводится к следующему. Реальной будем считать отражающую систему подложка—переход-ный слой—однородная пленка. Для параметров однородной пленки ( d f , n f ), переходного слоя ( d i , n i , kt ) и подложки ( d s , k s ) этой системы задаются конкретные значения и рассчитываются для них поляризационные углы Т э , А э , которые считаются "экспериментальными". В отличие от поляризационных углов реального эксперимента они не содержат истинных экспериментальных ошибок. Чтобы оценить эффект, возникающий в результате пренебрежения переходным слоем, обратную задачу относительно параметров d f и n f однородной пленки решаем для упрощенной модели подлож-ка—однородная пленка, не содержащей переходного слоя. Для упрощенной модели с теми же значениями параметров однородной пленки и подложки, что в реальной модели, рассчитываем поляризационные углы Т0, А 0. При решении обратной задачи для упрощенной модели относительно параметров d f и n f пленки углам Т 0 , А 0 соответствовали бы истинные значения параметров пленки. Но обратную задачу для упрощенной модели, очевидно, необходимо решать с "экспериментальными" значениями поляризационных углов Т э , А э . В этом случае величины
5 Т э = Т э -^ 0 ,
5 А э = А э -А 0
как бы играют роль "экспериментальных " ошибок, искажающих в упрощенной модели значения параметров пленки. Определяя в процессе решения об- ратной задачи df и nf для упрощенной модели по значениям Тэ, А э и зная их истинные значения, находим в результате ошибки этих параметров 8df и 8nf.
Аналогичным образом, рассматривая реальную модель подложка—однородная пленка, можно оценить влияние ошибок в задании оптических постоянных подложки ( ns и ks ) на точность определения параметров пленки d f и n f . В этом случае, как и в предыдущем, для реальной модели рассчитываются углы Ψ э , Δ э , а для упрощенной модели, которая отличается от реальной только введенными ошибками для оптических констант подложки 8n s и 8ks , рассчитываются углы Т0, А 0 . И здесь величины (3) играют роль "экспериментальных" ошибок, искажающих в упрощенной модели значения параметров пленки. Определенные в процессе решения обратной задачи (для упрощенной модели по значениям Ψ э , Δ э ) параметры пленки d f и n f будут отличаться от истинных значений, задавая ошибки 8d f и 8n , обусловленные неточностью в задании оптических постоянных подложки.
Можно рассмотреть и суммарный эффект, обусловленный пренебрежением переходным слоем и неточным заданием параметров подложки.
Созданная на этой основе математическая программа позволила провести численный эксперимент, который полностью подтвердил качественные выводы, сделанные в этой работе. Численный эксперимент показал также, что роль неучтенного тонкого переходного слоя на границе раздела подложка—пленка и неточностей в задании оптических констант подложки возрастает с уменьшением толщины пленки, перекрывая при определенных условиях влияние чисто экспериментальных ошибок. В этом плане большой интерес представляют экспериментальные исследования сверхтонких поверхностных пленок в рамках упрощенной модели подложка—пленка.
ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА
Теоретический анализ, проведенный в данной работе для сверхтонких поверхностных пленок, нашел яркое подтверждение при экспериментальном исследовании образцов, каждый из которых представляет собой сверхтонкую пленку SiO 2 на кремнии.
Рассмотрим первую группу из пяти образцов Si—SiO2. Поляризационные углы Т и А , измеренные для всех образцов на пяти углах падения (от 50 ° до 70 ° через 5 ° ), представлены в табл. 1.
Считая оптические константы кремниевой подложки на длине волны X = 632.8 нм известными:
n s = 3.865, k s = 0.023, (4)
определим толщину d и показатель преломления пленки n , используя обычный подход к решению обратной задачи, например метод Бокса с пошаговой минимизацией [4]. Сделаем это на каждом угле падения и на наборе углов падения, учитывая, что обратная задача с функционалом невязки, определенном на наборе углов падения, дает в определенном смысле (но не в арифметическом) усредненные по углам падения результаты ( d ср и n ср ). Окончательные итоги приведены в табл. 2. Как следует из табл. 2, для первой группы образцов реализуется одна из описанных выше ситуаций. Для образцов этой группы показатель преломления пленки n ^ 1, а ее толщина d достигает значений 30–35 нанометров. Особенно резко это проявляется для предельно тонких пленок с реальными толщинами 1.6–3 нм. С увеличением толщины эффект этого рода уменьшается, сохраняясь до реальных толщин = 10 нм.
Табл. 1. Поляризационные углы для 1-й группы образцов Si—SiO 2
|
Номер образца |
Т , А |
Угол падения |
||||
|
50° |
55° |
60° |
65° |
70° |
||
|
1 |
Т |
31° 28' |
27° 50' |
23° 18' |
17° 42' |
10° 32' |
|
А |
178° 55' |
178° 33' |
177° 58' |
177° 02' |
174° 33' |
|
|
2 |
Т |
31° 32' |
27° 52' |
23° 23' |
17° 48' |
10° 37' |
|
А |
178° 17' |
177° 52' |
177° 02' |
175° 38' |
172° 03' |
|
|
3 |
Т |
31° 31' |
27° 52' |
23° 24' |
17° 48' |
10° 37' |
|
А |
177° 56' |
177° 18' |
176° 16' |
174° 20' |
169° 41' |
|
|
4 |
Т |
31° 29' |
27° 52' |
23° 22' |
17° 46' |
10° 46' |
|
А |
176° 56' |
175° 28' |
174° 00' |
171° 04' |
163° 38' |
|
|
5 |
Т |
31° 28' |
28° 00' |
23° 46' |
18° 41' |
12° 50' |
|
А |
170° 31' |
167° 20' |
162° 20' |
154° 26' |
136° 31' |
|
Табл. 2. Параметры пленки SiO 2 на образцах 1-й группы
|
Номер образца |
Угол падения |
d (нм) |
n |
d ср (нм) |
n ср |
|
1 |
50° |
14.31 |
1.029 |
17.82 |
1.022 |
|
55° |
31.02 |
1.013 |
|||
|
60° |
5.20 |
1.088 |
|||
|
65° |
22.16 |
1.018 |
|||
|
70° |
26.39 |
1.015 |
|||
|
2 |
50° |
40.60 |
1.018 |
27.93 |
1.023 |
|
55° |
35.38 |
1.018 |
|||
|
60° |
35.30 |
1.018 |
|||
|
65° |
44.48 |
1.014 |
|||
|
70° |
31.74 |
1.020 |
|||
|
3 |
50° |
29.37 |
1.030 |
26.37 |
1.032 |
|
55° |
26.51 |
1.032 |
|||
|
60° |
30.86 |
1.027 |
|||
|
65° |
29.24 |
1.029 |
|||
|
70° |
24.55 |
1.035 |
|||
|
4 |
50° |
9.61 |
1.170 |
8.32 |
1.223 |
|
55° |
13.62 |
1.125 |
|||
|
60° |
8.94 |
1.201 |
|||
|
65° |
6.04 |
1.371 |
|||
|
70° |
6.76 |
1.305 |
|||
|
5 |
50° |
14.99 |
1.597 |
17.43 |
1.421 |
|
55° |
17.02 |
1.438 |
|||
|
60° |
18.15 |
1.397 |
|||
|
65° |
19.29 |
1.347 |
|||
|
70° |
17.45 |
1.422 |
Табл. 3. Поляризационные углы для 2-й группы образцов Si—SiO2
|
Номер образца |
Ψ , ∆ |
Угол падения |
||||
|
50° |
55° |
60° |
65° |
70° |
||
|
1 |
Ψ |
31° 26' |
27° 47' |
23° 16' |
17° 37' |
10° 26' |
|
∆ |
178° 56' |
178° 33' |
178° 04' |
177° 02' |
174° 39' |
|
|
2 |
Ψ |
31° 27' |
27° 49' |
23° 17' |
17° 39' |
10° 31' |
|
∆ |
177° 57' |
177° 15' |
176° 11' |
174° 15' |
169° 15' |
|
|
3 |
Ψ |
31° 27' |
27° 47' |
23° 18' |
17° 46' |
10° 40' |
|
∆ |
176° 36' |
175° 27' |
173° 44' |
170° 35' |
163° 40' |
|
|
4 |
Ψ |
31° 30' |
27° 59' |
23° 36' |
18° 33' |
12° 41' |
|
∆ |
170° 17' |
166° 56' |
161° 58' |
153° 33' |
135° 29' |
|
Объяснить полученные результаты можно как наличием очень тонкого и оптически менее плотного по сравнению с пленкой переходного слоя на границе раздела пленка—подложка, так и неточно заданными параметрами подложки. Влияние очень тонкого переходного слоя очевидно, но действуют оба фактора.
Табл. 4. Параметры пленки SiO 2 на образцах 2-й группы
|
Номер образца |
Угол падения |
d (нм) |
n |
d ср (нм) |
n ср |
|
1 |
50° |
1.87 |
2.90 |
2.48 |
3.13 |
|
55° |
2.02 |
2.98 |
|||
|
60° |
1.76 |
2.86 |
|||
|
65° |
2.13 |
3.05 |
|||
|
70° |
2.39 |
3.19 |
|||
|
2 |
50° |
2.92 |
1.66 |
3.77 |
2.76 |
|
55° |
3.32 |
1.46 |
|||
|
60° |
2.91 |
2.31 |
|||
|
65° |
2.89 |
2.26 |
|||
|
70° |
2.97 |
2.33 |
|||
|
3 |
50° |
5.12 |
1.63 |
4.74 |
2.25 |
|
55° |
4.76 |
2.00 |
|||
|
60° |
4.71 |
1.98 |
|||
|
65° |
5.64 |
1.48 |
|||
|
70° |
4.48 |
1.94 |
|||
|
4 |
50° |
16.02 |
1.54 |
15.06 |
1.64 |
|
55° |
16.87 |
1.48 |
|||
|
60° |
15.34 |
1.62 |
|||
|
65° |
16.28 |
1.53 |
|||
|
70° |
15.02 |
1.64 |
Обратимся теперь ко второй группе из четырех образцов Si—SiO 2 . Значения поляризационных углов для каждого образца на пяти углах падения указаны в таблице 3.
Окончательные итоги для этой группы, полученные тем же путем, что и для первой группы образцов, представлены в таблице 4.
Как следует из этой таблицы, для образцов второй группы реализуется уже вторая из описанных выше ситуаций. Результаты здесь также нереальные, хотя и несколько другого характера. В этом случае для каждого угла падения n → 3 , а толщина d изменяется относительно мало. Этот эффект также особенно отчетливо проявляется для предельно тонких пленок, сохраняясь до толщин ≈ 10 нм. Полученные результаты, как и в случае образцов первой группы, можно объяснить совместным влиянием очень тонкого, но уже оптически более плотного (по сравнению с пленкой) переходного слоя и неточностей в задании оптических постоянных кремниевой подложки.
Исследуя реальные образцы со сверхтонкими пленками, нельзя забывать и о влиянии чисто экспериментальных ошибок в определении поляризационных углов Ψ и Δ. Для сверхтонких пленок это влияние, конечно, огромно. В то же время систематичность бросков в значениях параметров пленки, наблюдаемых как для образцов первой, так и образцов второй группы, может быть объяснена прежде всего суммарным влиянием неучтенного переходного слоя и ошибок в задании оптических постоянных подложки.
Эффект, наблюдаемый при исследовании сверхтонких пленок и обусловленный совместным влиянием экспериментальных ошибок в определении углов Ψ и Δ, неучтенного переходного слоя и неточного задания оптических постоянных подложки, очевидно, должен ослабевать с увеличением толщины пленки. В некоторой степени, если судить по значению показателя преломления пленки, это проявляется уже на четвертом и пятом образцах первой группы и четвертом образце второй группы.
ЗАКЛЮЧЕНИЕ
Таким образом, выявленные нереальные и даже абсурдные результаты как численного, так и реального экспериментов говорят о математической некорректности задачи по определению параметров сверхтонких пленок. Для получения физически обоснованных результатов необходимо отказаться от классического подхода к решению обратной задачи для сверхтонких поверхностных пленок и перейти для этого случая к использованию методов решения некорректных математических задач.
Список литературы О характере математической некорректности обратной задачи эллипсометрии для сверхтонких поверхностных пленок
- Ржанов А. В., Свиташев К. К., Семененко А. И. и др. Основы эллипсометрии. Новосибирск: Наука, 1979. 422 с.
- Бобро В.В., Мардежов А.С., Семененко А.И. Обратная задача эллипсометрии для сверхтонких поверхностных пленок//Автометрия. 1997. № 1. С. 50-52.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 185 с.
- Box M.J. A new method of constrained optimization and a comparison with other methods//Comp. Journ. 1965. V8. P. 42-51.


