О качестве аппроксимации данных с периодической составляющей

Аппроксимация временных рядов различной природы является необходимой частью различных исследований, посвященных анализу данных и прогнозированию. Многие процессы обладают периодичностью, которая отражается в получаемых наблюдениях, и вносит существенный вклад в формирование временных рядов, описывающих эти процессы. Существует много достаточно точных методов аппроксимации временных рядов с периодической составляющей: SSA [1, 2], спектральный анализ [3] и другие методы, основанные на цифровой фильтрации. Но применение этих методов требует или доступа к платным пакетам прикладных программ, или серьезной математической подготовки для их самостоятельной реализации, поэтому многие специалисты сталкиваются на этапе аппроксимации с определенными трудностями. Одним из самых известных и простых методов аппроксимации временных рядов с периодической составляющей является тригонометрическая регрессия. Этот метод до сих пор развивается и дополняется [4], но различные модификации метода связаны с априорными сведениями о структуре ряда. Рассмотрим простейший случай, когда исследователь не обладает глубокими математическими знаниями и не знает ничего о данных, кроме периода.

В качестве примера возьмем временные ряды с ярко выраженной периодичностью – среднемесячные значения температуры воздуха, полученные на 134 метеорологических станциях на Азиатской территории России за 44 года, начиная c 1966 года. Перед аппроксимацией периодической составляющей из рядов были исключены линейные тренды, все коэффициенты при переменной оказались незначимы.

К данным были применены три метода выделения периодической составляющей: тригонометрическая регрессия Фурье, сезонный эффект и сезонное сглаживание.

В первом методе анализ ряда производится с помощью линейных комбинаций функций времени – синусов и косинусов. Периодическая составляющая ряда y аппроксимируется функцией следующего вида [5]:

m - 1

g ( t ) = a 0 + 2

j = 1

a 2 j - i cos

~ t + a, к m 7

sin

~1

к m 7

+ a m - 1

T ,

где m - период тренда, T - длина ряда. Коэффициенты имеют вид:

a

1T

о = ^^yt

T =

2V™2n a2j-1   y^yytcos j t• j 1,.", 21 •

2       2njm a2j =jLytsin^rt • J = V^y-1 •

1T am -1 =-E yt (-1) • T t=1

При использовании метода сезонного эффекта периодический тренд g(t) можно определить однозначно соотношением [6]:

у h - 1 g^(t) = ТЕ y t + mj h j = 0

_T ^ ^y i • t = 1,

T i = 1

m,

T где h = —, то есть вычисляется m значений, которые повторяются до конца ряда.

Метод сезонного сглаживания состоит в использовании отклонений от сглаженных значений. Соответствующие оценки для периодического тренда g(t) опять же определяются вычисленными m значениями, которые затем повторяются. Значения g ( t ) вычисляются по следующим формулам [6]:

h — 1

h - 1

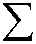
t + m j

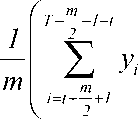
1 (

+- y

2 t

t +

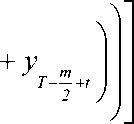
t = 1,

m

"2 ’

h - 1

h - 2

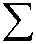
t + m j

m

m t +—

+ - y 2 t

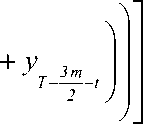
m,

где y * —

m

m

E y + i +^ y

=— m + 1         ² V ¹

m

m t+

m

, t —    + 1

,...

m

,T -—- скользящее среднее

с m членами.

В таблице 1 приведены средние абсолютные ошибки аппроксимации и прогнозирования на 12 лет тремя рассмотренными методами для четырех рядов, полученных на станциях в Томске, Диксоне, Оймяконе и Хабаровске. Ошибки вычислены по формуле:

T

X — 7 Ely - -y-b

T - — 1

где T – число элементов временного ряда, y – значение ряда в момент i , y ˆ – прогноз значения ряда в момент i .

Таблица 1

Средняя абсолютная ошибка	Томск	Диксон	Оймякон	Хабаровск
Регрессия Фурье	2.08	2.393	2.042	1.366
Сезонный эффект	2.08	2.393	2.042	1.366
Сезонное сглаживание	2.081	2.389	2.042	1.365
Прогноз регрессией Фурье	2.141	2.403	2.272	1.427
Прогноз сезонным эффектом	2.139	2.386	2.264	1.426
Прогноз сезонным сглаживанием	2.078	2.337	2.379	1.392

Ошибки, вычисленные при использовании регрессии Фурье и сезонного эффекта, одинаковы для всех рассмотренных рядов. Такой результат обусловлен тем, что в рассмотренных данных периодичность составляет больше 90 процентов, а линейный тренд предварительно удален.

В таблице 2 приведены ошибки прогнозирования временного ряда из среднемесячных значений температуры воздуха в Томске за 126 лет с 1875 г. по 2000 г.

Таблица 2

Интервал прогноза	Регрессия Фурье	Сезонный эффект	3-й метод
12 лет	2.306	2.292	2.279
24 года	2.243	2.236	2.226
36 лет	2.257	2.257	2.251
60 лет	2.188	2.184	2.184
80 лет	2.189	2.185	2.188

Как видно из приведенных таблиц, значения ошибки аппроксимации и прогноза очень близки.

На рисунке 1 приведена карта Азиатской территории России, на которой отмечены 134 метеорологические станции, где были получены исследуемые данные. Число, обозначающее станцию, – это относительная ошибка аппроксимации в процентах (в отношении к среднеквадратическому отклонению) ряда среднемесячного значения температуры, полученного на данной станции.

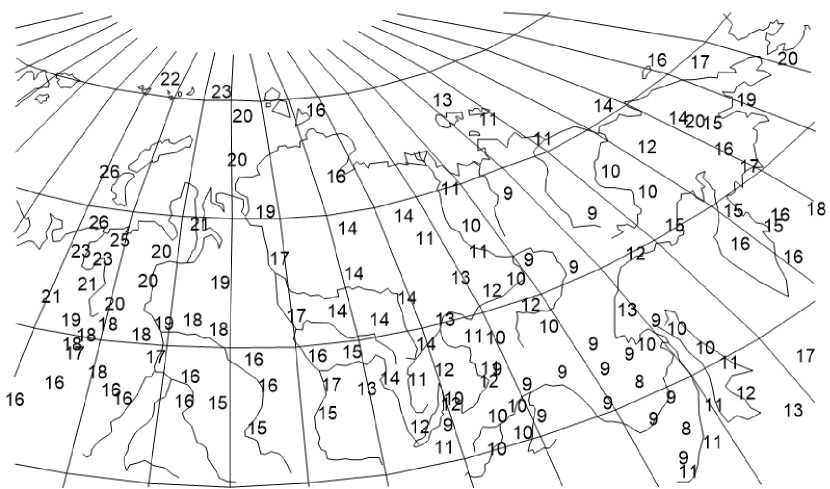
Рисунок 1  – Карта метеорологических станций с указанием относительной ошибки аппроксимации данных, полученных на этой станции.

Как видно из рисунка, масштаб ошибки скорее связан с географическим местоположением станции, где данные получены, то есть со спецификой рядов. Вариация ряда незначительно влияет на качество оценки – это видно на рисунках 2 и 3, на котором проиллюстрированы зависимости соответственно значения средней абсолютной ошибки и средней относительной ошибки аппроксимации от среднеквадратического отклонения ряда.

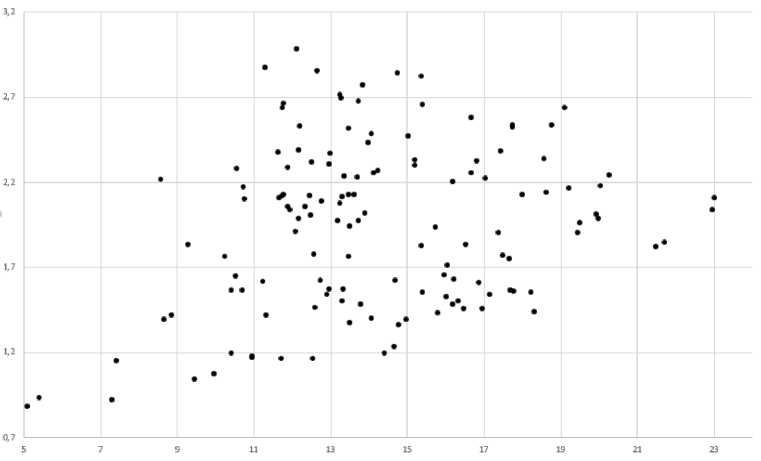
Рисунок 2 – Зависимость средней абсолютной ошибки аппроксимации от среднеквадратического отклонения ряда.

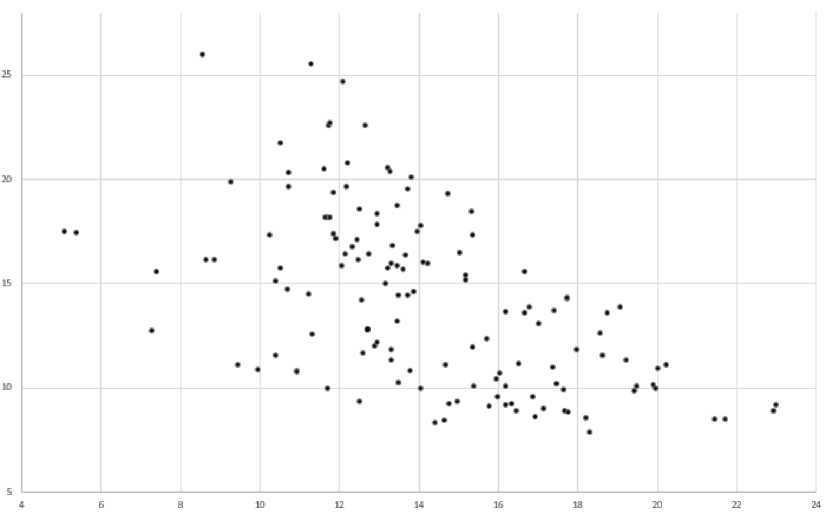
Рисунок 3 – Зависимость средней относительной ошибки аппроксимации от среднеквадратического отклонения ряда.

В заключение хотелось бы отметить, что результаты сравнения ошибок аппроксимации методов Фурье и сезонного эффекта показывают, что для рядов с сильной периодической составляющей можно использовать более простой второй метод без потери качества оценки.

Результаты были получены в рамках выполнения базовой части государственного задания Минобрнауки России, проект 8.9628.2017/8.9.