О классе графов, обладающих сильными перемешивающими свойствами
Автор: Исаев М.И., Исаева К.В.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Математика, информатика, управление, экономика
Статья в выпуске: 3 (19) т.5, 2013 года.
Бесплатный доступ
Рассматриваются три свойства перемешиваемости графа: большая алгебраическая связность, большая константа Чигера (изопериметрическое число) и большой спектральный зазор между 1 и вторым по величине собственным значением матрицы переходных вероятностей случайного блуждания по графу. В работе доказывается эквивалентность данных свойств (в некотором смысле). Получены оценки вероятности, что случайный граф обладает указанными свойствами перемешиваемости. Кроме того, приведены асимптотические формулы для числа эйлеровых ориентаций и числа эйлеровых циклов в неориентированном простом графе.
Алгебраическая связность, изопериметрическое число, матрица лапласа, эйлеровы циклы и ориентации
Короткий адрес: https://sciup.org/142185927
IDR: 142185927 | УДК: 519.17
Текст научной статьи О классе графов, обладающих сильными перемешивающими свойствами
Пусть G — неориентированный простой граф с множеством вершин VG и множеством ребер EG. Определим (п х п)-матрицу Q следующим образом:
Qjk =
-1, dj, 0
{vj,vk} E EG, j = k, в остальных случаях,
где п = | VG | ii dj обозиачас'т степень vj E VG. Матрица Q = Q ( G ) называется лштщщеи. Лапласа графа G. Собственные значения Ai < A2 < ... < An матрицы Q являются неотрицательными вещественными числами, причем количество нулевых собственных значений совпадает с количеством компонент связности, в частности, Ai = 0. Число А2 = A2(G) называется алгебраической связностью графа G.
Классическая теория алгебраической связности была, развита. Фидлером, см. [6], [7]. Отметим также, что число A2 (G) является дискретным аналогом наименьшего положительного собственного значения дифференциального оператора. Лапласа, на. римановом многообразии. (Для дополнительной информации о спектральных свойствах матрицы Лапласа см., например, [14] и ссылки, приведенные там.)
Пусть Т^ — множество простых графов G, обладающих следующим свойством.
Свойство 1. Алгебраическая связность A2(G) >y|VG|.
Для подмножества вершин А С VG пусть дА обозначает множество всех ребер, соединяющих вершину из А и вершину не из А:
дА = {{u, v} E EG :и E A,v EVG \ А} .
Константа Чигера (или изопериметрическое число) графа G, обозначаемая 4(G), определяется следующим образом:
«(G) = min { :А CVG, 0 <|А|<^}.
Число 4(G) является дискретным аналогом изопериметрической константы (Чигера) в теории римановых многообразий и имеет много интересных интерпретаций (для более подробной информации см., например, [13] и ссылки, приведенные там).
Пусть С^ — множество простых графов G, обладающих следующим свойством.
Свойство 2. Константа Чигера i(G) > 7|KG|.
Пусть Р = Р(G) обозначает матрицу переходных вероятностей случайного блуждания по графу G:
Р* ={*0
{о , ,v k } е EG, в остальных случаях.
Собственные значения Р таковы, что
1 = Х1 >Х 2 ••• >Х п > -1.
Граф G связен тогда и только тогда, когда случайное блуждание является неприводимой цепью Маркова. В этом случае существует единственное стационарное распределение и кратность собственного значения Х 1 = 1 равна одному. (Для дополнительной информации о случайных блужданиях на графах см., например, [9] и ссылки, приведенные там.)
Пусть М - — множество простых графов G, обладающих следующим свойством.
Свойство 3. Спектральной зазор 1 — X2(G) >7 и mind, > 7|KG|.
,
Известно, что графы из Т-, С-, М - имеют сильные перемешивающие свойства. Мы называем Т - ПС- ПМ--классом 7-перемешивающих графов. В действительности (см. раздел 2 настоящей работы), Свойства. 1-3 эквивалентны в следующем смысле: если граф удовлетворяет одному из этих свойств при 7 = 7о > 0, то он удовлетворяет всем свойствам 1-3 для некоторого 7 > 0, зависящего только от 70.
В разделе 3 оценивается вероятность случайного графа быть 7-перемешивающим. Рассматривается модель Гильберта, случайного графа: каждая пара, вершин может соединяться ребром независимо с некоторой фиксированной вероятностью 0 < р < 1. Оказывается, что в этой модели практически все графы (асимптотически) получаются 7-перемешивающими при некотором 7 > 0. зависящиэi только от р.
В разделе 4 построено общее семейство графов, удовлетворяющих свойствам 1-3 (см. пример 3 и замечание 1). Например, семейства полных графов {К п } и полных двудольных графов {К п,п } являются частными случаями этого общего семейства. В разделе 4 обсуждаются также другие важные примеры.
Кроме того, в настоящей работе рассматриваются две задачи перечисления: подсчет числа эйлеровых ориентаций (ЕО) и подсчет числа эйлеровых циклов (ЕС) в неориентированном простом графе. Известно, что обе эти задачи являются полными для класса #Р (см. [2], [10]) и, следовательно, трудными с точки зрения теории сложности.
В работах [4], [5] было определено асимптотическое поведение числа, эйлеровых ориентаций и числа эйлеровых циклов для случая 7-перемешивающих графов (точнее, для графов, удовлетворяющих свойству 1).
В разделе 5 приведены асимптотические формулы для ЕО, ЕС, а также проведено сравнение с точными значениями для небольших графов. В действительности, если граф G является 7-перемешивающим, то для любого е > 0 относительная погрешность |d(G)| < Сп-1/2+е, где С > 0 зависит только от е и 7. Доказательство этих формул можно найти в препринтах [e-print: hal-00730657] и [e-print: hal-00739760], планируемых для публикации в ближайшее время.
-
2. Эквивалентность свойств 1-3
Известно, что для простого графа Gen вершинами
п
(3a)
(3b)
А2 (G) <----- min d , ,
А2 (G) > 2 min d , — n + 2,
A2(G) < z(G) < ^G^imxdj^,
A2(G) < A2(Gi ) + 1, (5а)
A2(G) < А2(G ‘ ), (5b)
где Gi — граф, полу чающийся из G посредством удаления одной вершины и всех смежных ей ребер, G — произвольный граф такой, что V G‘ = VG и EG С EG.
Оценки (3), (5) были получены в [6]. Оценки (4) приведены в [13].
Используя (4) и неравенство dj < п, получаем, что для любого уо > 0
^70
С С71
11 ^70 С ^71 ,
где 7 i > 0 'зависит только от уо.
Пусть ж G R” и М — (п х п)-матрица. Мы используем обозначения:
||ж | = VЖ ж,
\\М || = sup | Мх | .
$GRn, ||Д | =і
Для того чтобы завершить доказательство эквивалентности Свойств 1-3, нам потребуется следующая лемма.
Лемма 1. Пусти a,bi,b2 > 0. Пусти А — симметричная положителино определенная (п х nj-матриир такая, что для некоторого о G R”. о = 0.
Ao = 0,
(7а)
и для любого u G R” такого. что iFw = 0.
|| Au| | > a ||u|| .
(7b)
Тогда для любой симметричной (п х п)"матрицы В такой, что
|| В || < bi и ЕТВЕ > Ь 2 |го |2 ,
(7с)
выполняется следующее утверждение:
I
det(A - АВ) = 0
А = 0
для некоторого р = р(а, bi,b2) > 0.
Доказательство леммы 1 приведено в конце данного раздела.
Заметим, что
Р = I - D- Q,(9)
где Q и Р - матрицы, определенные в (1) и (2) соответственно, I обозначает единичную матрицу п D — диагональная матрица.. Djj = dj.
Пусть Ai = 1Q, Bi = ^D и гоi = [1,..., 1]Т. Используя (9), получаем, что det(Ai - AI) = 0 ^^ det(Q - АпІ) = 0;
det(Ai - ABi) = 0 ^^ det(P - (1 - A)I) = 0
для любого u G Rn таког*). что uTrw i = 0.
uTAiu > —A2(G)uTu;(12)
п
||В1\ < — max dj < 1, wТ В1 wi > — min dj wTw 1.
Комбинируя свойство 1, (За), (10) - (13) и лемму 1, получаем, что для любого 79 > 0
Т70 С ^^4^2 ,
гл.° 72 > 0 'зависит то.тько от 79.
Пусть А2 = D-2 QD-2, В = nD-1 и w2 = D 2 w 1, г де Ds — диагональная матрица, Djj = (dj)s- Используя (9), находим, что det(A2 — АІ) = 0 ^^ det(P — (1 — А)7) = 0;
det(A2 — АВ2) = 0 ^^ det(Q — АпІ) = 0
для любого п Е R” такого, что бТ w2 = 0.
йТ А2П > (1 — X2(G))nTп;
\В2Н <----—, wTВ1ш2 = nwTw1 > wTw2.
min di j j
Комбинируя свойство 3, (15) - (18)
и лемму 1, получаем, что для любого 79 > 0
•М70 С Т73 ,
где 73 > 0 'зависит только от 79.
Собирая вместе (6), (14) и (19),
Теорема 1. Пусти Т7 , С7 , М7 любого 7о > 0
мв1 получаем искомое утверждение.
множества, рассматриваемые в разделе 1. Тогда для
Т70 и С70 и М70 С Т7 П С7 П М7, где 7 > 0 зависит тполько от 79.
Теперь осталось доказать лемму 1.
Доказательство. Пусть det(A — АВ) = 0. Тогда для некоторого б Е Rn, б = 0, Аб = АВб.
Пусть б = бц + бт, где б^ \| ши б^w = 0. Согласно (7а) имеем, что б^ Аб = 0.
Так как А = 0, используя (21), получаем, что б^ Вбц = —б^ Вбт.
Используя (7с), (22) и неравенство Коши-Шварца находим, что ь1НбНННбт\ > \б|\\Вб±\ > |б[ Вб = \бТВб|| > ь2\б|\2.
Поэтому имеем, что
«бт» > ^==И< V ь1 + ь2
Используя (7Ь), (7с) и (23), находим, что
»Аб» > а»6!»,
«Вб«< Ь1«б«<
w|±3 „бщ.
Ь2
Комбинируя (21) и (24), получаем, что ab2
А >. bi V bi + ь2
-
3. Вероятность случайного графа быть у-перемешивающим
Пусть £ — случайная величина, принадлежащая биномиальному распределению В (М,р):
М 'р к (1 - р) М - к , 0 <р< 1,М е N.
Рг (^ = fc) =
Заметим, что
Рг (^ < аМ ) < с
м
для некоторых а > 0, с > 1, зависящих только от р. опенки: для 1 < к < Р ( М +2 1)
Это следует, например, из следующей
Рг ^ = к)
Рг ^ = к — 1)
М—к + 1 р к 1 — р
≥
еЪ (м + 1) р 2
^2 (М + 1) 1 — р - .
Пусть G — случайный граф, принадлежащий модели Гильберта G(п,p):
V
i
<
i
Для подмножества вершин А С VG, используя (26), находим, что
Рг(|дА| < а|А|(п — |А|)) < с -| л | ( п -| л | 1
.
Используя (27), получаем, что
Рг(i(G) <
ап, т) <
≤
£ Рт(|дА|<а|А|П) <
A c VG, 0< | Л |< 5
£ £ гг(|8А|<а|А|(п - |А|)) <
≤
к=1 |A|=k n/2
Е п!
к!(п к=1 v
-
к) °
n/2 .-k(n - k) < £
для некоторого 3 > 1.
≤
(1 + c-n/2)n
— 1 < 3
-
к=1
n
'П'.
к!(П—к)!. (с " /2)к<
зависящего только
от р.
Согласно (28) и теореме 1, получаем, что вероятность случайного графа (в модели Гильберта G(n,p)) быть у-перемешивающим не менее чем 1 — 3-n, гДе У = У(р) > 0 и 3 = 3 (р) > 1-
-
4. Некоторые основные свойства и примеры
Заметим, что согласно (ЗЬ) и теореме 1, если min dj — ct|vg| то Граф G является у-перемешивающим для некоторого ^ > 1/2, Для некоторого у = у(а) > 0.
— два полных графа с п вершинами. Определим G^ следу-
Пример 1. Пусти Kn и Kn юхуим образом:
VG^ = VKn и VKn,
Edn1 = EKn и EKn U E+ , где E+ = {{щ, йг}, г = 1,..., п}.
Для G = Gn) имеем. нт<:> для всех j = 1,..., 2n dj = n + 1 > jVG'.i , однако
*(G®) |E + |
.vk ' 0 npnn ^^ /6 n ^
Поэтому семейство {G^)} не удовлетворяет свойству 2 (и, следовательно, свойствам 1, 3). Кроме того, отметим, что это семейство графов имеет также большую вершинную и реберную связность.
Пример 2. Пусть Кп — полный граф с n вершинами. Определим GTl следующим образом:
VG^ = VKn U{ v n+i} , EG ^2) = EKn U{vn,vn+i}.
Для G = Gn2) iimccai. что mindj = 1. олпако спектральный ’ва’вор> 1 — X2(Gn2)) — 1/2 при j n — 2. Примеры 1 и 2 показывают, в частности, что оба условия свойства 3 являются существенными.
Пример 3. Пусть G o — связный простой граф с т > 1 вершинам и. Пусть c i ,c 2 ,. — некоторые натуральные числа. Определим G^ следующим образом:
.
., cm
VG j3 = { v j : г = 1 ,..., ncj , j = 1 ,..., т } ,
{ v jl ,v j2} G EG® { v ,i ,v j2} G EG o .
Оценим константу Чигера (изопериметрическое число) z(G®). Пусть
т co = min щ, С = > щ .
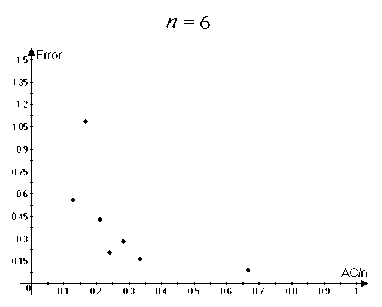
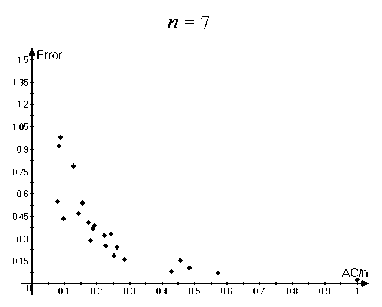
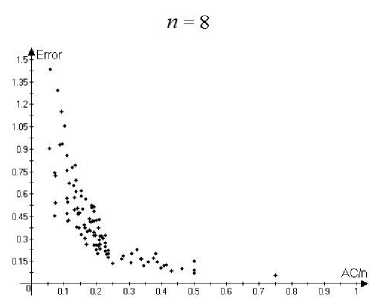
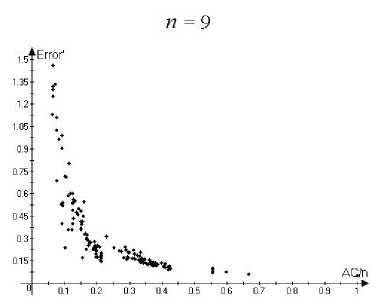
i Заметим, что степень каждой вершины V G^3) не менее con (29а) и |VG®| = Cn. (29b) Пусть А С VG^3). |А| < Cn/2. • Случай 1. |А| < con/2. Используя (29), находим, что 15А| — сНЛІ-ІД2 > фМ = co|VG®| 2С |А|. • Случаи 2. |А| > con/2. Пусть Vi,V2 С VGo такие, что vj G Vi < > | {vj : vj G А} | — con 2т, cjn . vj G V2 < > | {vj : vjG А} | — Используя con/2 < |А| < Cn/2. находим, что Vi UV2 = VGo, |Vi| > 0, |V2| > 0. Так как Go — связный, мьi можем найти vj1 G Vi, vj2 G V2 такие, что {vj1, vj2} G EGo. Оценивая число ребер в ӘА, соответствующих этим вершинам, получаем, что cocj2n2 Д2Д c^lVU^I |- 4т > 2тС|А| 2тС2 |А|. Комбинируя (30), (31) и теорему 1, получаем, что семейство свойствам 1-3 с у > 0, зависящим только от Gq, ci,..., cm. { VG^ удовлетворяет Отметим также, что пример 3 может быть модифицирован таким образом, что константы ci,... ,cm > 0 необязательно являются натуральными числами. Мы предположили это только для простоты доказательства. Замечание 1. Комбинируя (5), теорему 1 и пример 3, момсно доказать свойства 1-3 для большого числа классических примеров (включая семейства {Кп}, {Kn,n} и множество других). 5. Асимптотические оценки для у-перемешивающих графов 5.1. Эйлеровы ориентации Эйлерова ориентация графа G — такая ориентация его ребер, что для любой вершины число входящих ребер и выходящих ребер одинаково. Обозначим EO(G) — число эйлеровых ориентаций, эйлеровы ориентации полного графа Кп называются регулярными турнирами. Эйлеров цикл в графе G — замкнутый путь, который использует каждое ребро G ровно один раз. Обозначим EC(G) — число различных эйлеровых циклов с точностью до циклического сдвига. Известно, что EO(G) = EC(G) = 0, если степень хотя бы одной вершины графа G нечетная (для дополнительной информации см., например, [1]). В этом разделе мы везде предполагаем, что все вершины графа имеют четную степень. Рассматрим две задачи перечисления: подсчет числа эйлеровых ориентаций и подсчет числа эйлеровых циклов в неориентированном простом графе. Известно, что обе эти задачи являются полными для класса #Р, см. [2], [10]. Результаты, представленные в этой секции, основаны на оценках из [4], [5]. Доказательства можно найти в препринтах [e-print: hal-00730657] и [e-print: hal-00739760], планируемых для публикации в ближайшее время. Известно, что задача подсчета числа эйлеровых ориентаций может быть сведена к подсчету числа полных паросочетаний такого класса двудольных графов, для которых это может быть сделано приближено с большой вероятностью за полиномиальное время, см. [10]. Однако степень соответствующего полинома большая, и поэтому, в действительности, эти алгоритмы имеют большое время работы при уровне относительной погрешности О(п-1/2). Для у-перемешивающих графов верна следующая асимптотическая формула. Утверждение 1. Пусть G — неориентированный простой граф с п вершинами V1, v2, ..., Vn, имеющими четную степень. Пусть G также является у-перемешивающим графом для некоторого у > 0. Тогда EO(G) = (1 + 5(G)) 2IEGI + ^-1 ^-1 1 7Ж) П Ра {у Xk }EEG Р' = 1 4(d, + 1)2 2(dj +1)(dk + 1) 4(dk + 1)2 , где dj обозначает cmепень вершины щ, t(G) — число остовнь.ix деревьев графа G, и для любого е > 0 |5(G)| < Cn-1/2+e, где константа C > 0 зависит тполько от у и е. Замечание 2. Отметим, что согласно теореме Кирхгофа (матричной теореме о деревьях), см. [8], имеем, что t(G) = —A2A3 • • • An = det М11, п где Мр — минор матрицы Q, получающийся посредством удаления первой строки и первого столбца. Замечание 3. Для полного графа A2(Кп) = п, ЕКп = ^2-1), t(Kn) = пп-2, П р- = (1 - 4П2 - 21 Д <ик }ЕЕК„ 1 4п2 ) п(п— 1) 2 п(п— 1) 2 = е 1/2 + О(п 1). Результат утверсисдения 1 для этого случая сводится к результату из [12] о подсчете числа регулярных турниров в полном графе. Подробное доказательство утверждения 1 приведено в препринте [e-print: hal-00730657]. В настоящей работе мы только проводим сравнение ответов, полученных с помощью формулы (32) с точными значениями для маленьких графов. Пусть Error(G) = ЕО approx (G) - EO(G) EO(G) где EOapprox(G) соответствует правой части (32). Следующие графики (см. рис. 1) демонстрируют зависимость Error(G) от отношения A2(G)/n, где A2(G) — алгебраическая связность и п = | VGI =6, 7, 8, 9: Рис. 1. Зависимость Error(G) от отношения A2(G)/n Графики из рис. 1 показывают, в частности, что Error значительно убывает при возрастании A2(G)/п. 5.2. Эйлеровы циклы В отличие от эйлеровых ориентаций даже приближенные и вероятностные эффективные алгоритмы для подсчета числа эйлеровых циклов в общем случае до сих пор не были получены в литературе и известны толвко для специальных классов графов, обладающих невысокой плотностью, см. [3] и [15]. Тем не менее, для у-перемешивающих графов верна асимптотическая формула для ЕС(G), аналогичная (32). Это формула немного более сложная, поэтому нам потребуются некоторые дополнительные обозначения. Пусть W = Q-1 = (Q + J )-1, где Q — матрица Лапласа и J обозначает матрицу, все элементы которой равны 1. Пусть a = («1,..., an) € Rn такой, что aj = ^зз. Пусть В = Qa л С1 = exp (- £ £ <.В I , ,33) j=1 k=j+1 (п В2 \ -£ 2№+Щ I' 3=1 где dj — степеіп> вершины Vj € VG. Пусть ад = €г(л(д)^ л(д)^), где tr(•) — след матрицы, Л(Ө) обозначает диагональную матрицу с элементами на диагонали, равными компонентам вектора QӨ. Пусть Дб = (е^,..., еД)) € Rn такое, что ejfc) = Sj^. г,те 5jk — символ Кропокера. Пусть т^ = Д(е(^)). Сз = exp п ∑︁ 3=1 т3 2(dj + 1) Наконец, пусть С4 = П Рзк, {«з ,«k\^EG где Pjk такое же, как и в (32). Утверждение 2. Пусти G — неориентированный простой граф с п вершинами V1,V2,..., vn, имеющими четную степени. Пусти G такоюе является у-перемешивающим графом для некоторого у > 0. Тогда (п П (м3 - 1)!2|eg|-^-1к-2-1 .'.С-ОШС I , (37) 3=1 ) где. С1,С2,Сз,С4 определены о (33). (34). (35). (36) соответственно, dj обозначает степень вершины Vj. t(G) — число остовных деревьев G. и для любого е > 0 |5‘(G)| < С‘п-1/2+е, где константа С‘ > 0 зависит только от у и е. Замечание 4. Мосисно получить для случая G = Кп, что С1С2С3 С4 = 1+ О(п-1). Используя замечание 3 и формулу Стирлинга для факториалов, результат из утвер-мсдения 2 для этого случая момсет быть сведен к результату из [И] о подсчете числа эйлеровых циклов в полном графе. Подробное доказательство утверждения 2 приведено в препринте [e-print: hal-00739760]. В настоящей работе мы только проводим сравнение ответов, полученных с помощью формулы (37), с точными значениями для маленьких графов. Пусть Error'(G) = ЕС approx (G) - ЕС(G) ЕС (G) где EСapprox(G) соответствует правой части (37). Следующие графики (см. рис. 2) демонстрируют зависимость Error'(G) от отношения A2(G)/n, где A2(G) — алгебраическая связность и п = | VGI =6, 7, 8, 9: Рис. 2. Зависимость Error' (G) от отношения A2(G)/n Графики из рис. 2 показывают, в частности, что Error' значительно убывает при возрастании A2(G)/п.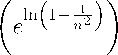
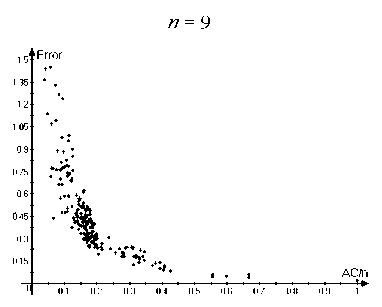
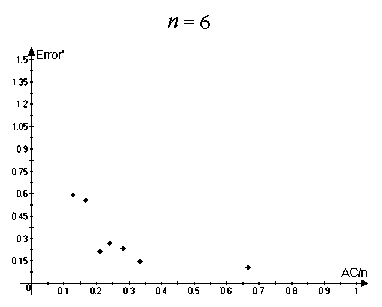
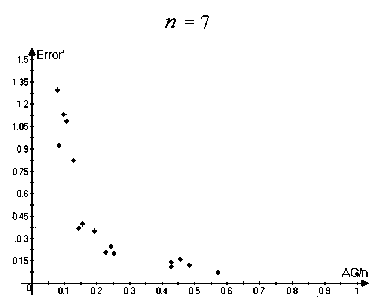
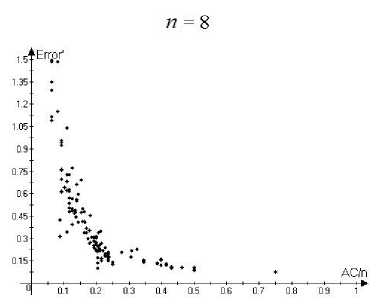
Список литературы О классе графов, обладающих сильными перемешивающими свойствами
- Biggs N.L., Lloyd E.K., Wilson R.J. Graph Theory//Clarendon Press, Oxford. -1976. -P. 1736-1936.
- Brightwell G., Winkler P. Note on Counting Eulerian Circuits//Proceedings of the 7th ALENEX and 2nd ANALCO 2005, ALENEX/ANALCO 2005. Vancouver, BC, C Demetrescu. R. Sedgewick and R. Tamassia (eds.). -2005. -P. 259-262. -e-print: arXiv:cs/0405067.
- P. Chebulu, M. Cryan, R. Martin, Exact counting of Euler tours for generalized series-parallel graphs//Journal of Discrete Algorithms. -2012. -V. 10. -P. 110-122.
- Isaev M.I. Asymptotic behaviour of the number of Eulerian circuits//Electronic Journal of Combinatorics. -2011. -V. 18(1). -P. 219.
- Исаев М.И. Асимптотическое поведение числа эйлеровых ориентаций в графах//Математические заметки. -2013. -Т. 93. -В. 6. -C. 828-843.
- Fiedler M. Algebraic connectivity of graphs//Czech. Math. J. -1973. -V. 23(98). -P. 298-305.
- Fiedler M. Laplacian of graphs and algebraic connectivity//Combinatorics and Graph Theory. -1989. -V. 25. -P. 57-70.
- Kirchhoff G. Uber die Aufl¨osung der Gleichungen, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Str¨ome gef¨uhrt wird//Ann. Phys. Chem. -1847. -V. 72. -P. 497-508/Translated by J. B. O’Toole in I.R.E. Trans. Circuit Theory, CT-5. -1958. -V. 4.
- Lovasz L. Random walks on graphs: A survey//Combinatorics, Paul Erd¨os is eighty. -1993. -V. 2. -P. 1-46.
- Mihail M., Winkler P. On the number of Eulerian orientations of a graph//Algorithmica. -1996. -V. 16. -P. 402-414.
- McKay B.D., Robinson R.W. Asymptotic enumeration of eulerian circuits in the complete graph//Combinatorics, Probability and Computing. -1998. -V. 7(4). -P. 437-449.
- McKay B.D. The asymptotic numbers of regular tournaments, eulirian digraphs and eulirian oriented graphs//Combinatorica. -1990. -V. 10(4). -P. 367-377.
- Mohar B. Isoperimetric numbers of graphs//J. Combin. Theory Ser. B. -1989. -V. 47. -P. 274-291.
- Mohar B. The Laplacian spectrum of graphs//Graph Theory, Combinatorics, and Applications. -1991. -V. 2/Ed. Y. Alavi, G. Chartrand, O. R. Oellermann, A. J. Schwenk. -P. 871-898.
- P. Tetali, S. Vempala, Random sampling of Euler tours//Algorithmica. -2001. -V. 30. -P. 376-385.


