О компьютерном моделировании микрофлюидных систем

В развитие работ [1, 2] в данной статье приводятся результаты моделирования микрофлюидной системы осесимметричной и плоской геометрии. Распространенная на практике процедура ввода пробы (стекинг) посредством электрического поля формирует струйное течение на входе в капилляр, и возникает необходимость анализа струйных потоков в микрофлюидных системах.

Микрофлюидные системы с выпуском представляют интерес при изучении электрокинетиче-ских течений в сложных геометрических конфигурациях с различными граничными условиями. В этой статье представлен анализ влияния инерционных эффектов и реологии в электрокинети-ческих течениях. В стандартных приложениях микрочипов поле электрокинетического потока можно разделить на внутреннюю область, где доминируют вязкие и электростатические силы, и внешнюю область, где доминируют силы инерции и силы давления. Эти две области разделяются условиями для скорости скольжения, которые определяются уравнением Гельмгольца—Смо-луховского. Справедливость этого предположения исследуется посредством анализа поля скоростей в двумерных течениях в канале с движением за счет давления и импульсным запуском электрического поля. Определены условия аналогии между полем скоростей и электрическим полем: однородный поверхностный заряд, малые числа Рейнольдса и Струхаля, однородные свойства жидкости, нулевой перепад давления между входом и выходом.

Электрокинетика представляет собой движение жидкости относительно фиксированной заряженной сплошной поверхности. Это движение происходит в том случае, когда электрическое поле прилагается к электрическому двойному слою, который спонтанно образуется при взаимодействии жидкости и поверхности при их контакте. Толщина этого двойного слоя определяется противоположно направленными силами электростатического притяжения и тепловой диффузии, а также реологией смеси и некоторыми другими факторами и имеет значение порядка длины Дебая. При разработке микрофлюидных техноло- гий целесообразно использовать электрокинетиче-ский механизм в качестве метода контроля жидкостей в чипах микрофлюидных систем. Электро-кинетическая подача смеси в чипах широко используется при электрофоретическом и хроматографическом разделениях и в других "микрочипо-вых лабораториях", имея существенные преимущества по сравнению с автономными капиллярными системами, включая возможность мультипликации сетевых канальных потоков и уменьшения времени анализа.

В связи с обозначенным преимуществом чипов весьма актуален анализ процедуры ввода пробы (стэкинг) и учет реологии смеси, что является необходимым при анализе биологических жидкостей.

В различных исследованиях относительно теории электроосмотических потоков были проанализированы эффекты инерции потока, градиентов давления, неоднородность Z -потенциала в микро-флюидных каналах.

ФОРМУЛИРОВКА ПРОБЛЕМЫ

Анализ работ, посвященных течению в микро-флюидных системах показывает, что инерционные силы играют немаловажную роль. Процедура ввода пробы (стекинг) в микрочиповый крест несомненно носит струйный характер [3]. Струе -видная форма пробы формируется посредством электрических сил в поперечном сечении перпендикулярно направлению ее ввода. Учет электрических сил микрофлюидных систем в уравнении движения можно осуществить двояким путем [4]. Первый — разбиение на две зоны области течения: в первой, прилегающей к стенке капилляра, пренебрежимо малы силы инерции и имеет место баланс сил давления, вязкости и электрических сил; во второй, вдали от стенки, силы инерции сравнимы с остальными, число Рейнольдса порядка единицы и более, а электрические силы стремятся к нулю на оси капилляра. Второй путь — более целесообразен при компьютерном моделировании микрофлюидных систем: моделирование электрических сил во всем профиле течения в капилляре. Помимо этого, в компьютерной модели учитывается тепловыделение при течении пробы с буфером в капилляре — наличием архимедовых сил в уравнении движения; наличие частиц (необходимое условие возникновения электрофореза) моделируется отрицательной архимедовой силой.

В данной статье в продолжение работ [1, 2] описывается компьютерное моделирование течения в микроканале с учетом электрических сил.

УРАВНЕНИЯ КОМПЬЮТЕРНОЙ МОДЕЛИ

Уравнения компьютерной модели микрофлю-идной системы имеют вид:

∂u∂

ρ⋅u⋅    +ρ⋅v⋅=

∂x∂

_ д p   1 д i дт

=--+--" — (У " —) + Fn + F л, дx  yi дУ^ дy^

р. ^y-jul + р .^Tv=о, ∂x∂

F q = q - E , F a = в "  g -A T ,

ρ ⋅ c p

∂∆T∂∆

⋅ u ⋅      + ρ ⋅ c ⋅ v ⋅

∂x       p∂ a ∂∂∆

— (y)

yi ∂y∂

∂C      ∂СD

ρ⋅u⋅    + ρ⋅v⋅=

∂x         ∂yy

∂     ∂ С

У⁽ y "  ^), ∂ y     ∂ y

i = 0 — плоская геометрия; i = 1 — осесимметричный случай.

Рассматривается течение пассивной смеси пробы с буфером или течение смеси с незначительной скоростью химической реакции.

Следует заметить, что трансформация уравнений Навье—Стокса в уравнения пограничного слоя обусловлена тем, что длина капилляра много больше его характерного поперечного размера, т. е. продольный масштаб много больше поперечного. Можно показать, что в этом случае вторые производные от скорости, избыточной температуры и концентрации пробы по продольной координате малы по сравнению со второй производной по поперечной координате: по терминологии Сантьяго X. [4] — во второй зоне, вдали от стенки капилляра.

Граничные условия:

u = u _G, C = 0, A T = 0    для y ^^ ;

д и _ д С      дА T _           _(2)

— = 0, — = 0, --- = 0 для y = 0.

,,

∂y      ∂y∂

Начальные условия:

x = 0, и = и 0, C = 0 для |y| < d;(3)

и = 0, C = 0 для |y | >  d .

Интегральные соотношения для рассматриваемой системы имеют следующий вид.

Для импульса:

те                     те

Р • J и2 • у • dу =J (Fq + FA) • у • dy;

для массового расхода:

те

р - J u • C • у • dу = const = G0.

Наличие инвариантов струйного течения позволяет получить численное решение задачи (1) при автоматическом контроле счета.

Введем замену переменных:

q = x, n = [2 J C • u • у • dу ] .

Запишем уравнение переноса импульса в новых переменных (2-я зона):

I u              I        I u .

— = ( C 2 / n ) —( uy ²—) +

Iq         In     ПIn

+ ( C / n ²)(1 - 1/Sc)( uy ² | u I C ) + дп In

+ (Gr/Re) A T / u.                     (4)

Аналогично преобразуется уравнение конвективной диффузии и переноса избыточного теплосодержания:

^| C = ( C ²/Sc • n ) C- ( uy¹ dq             In

IC ) nIn

^ = (aT2 Pr^n)C-fuyу iq              In

I2AT1 n • In

А поперечная компонента скорости v определяется из уравнения неразрывности:

v = - u / у (1/ u ²) C-I n

у=

„ , ( 2 I u C / n uy

v v    In

dn -

-

(Gr/Re)( u / у ) J|^

12 г ndn J u • C

ⁿ d n , u ³

(Все величины безразмерны. В качестве масштаба скорости, температуры, концентрации выбраны их начальные значения на входе в капилляр, а в качестве масштаба длины — диаметр капилляра).

Начальные и граничные условия в новых переменных имеют вид:

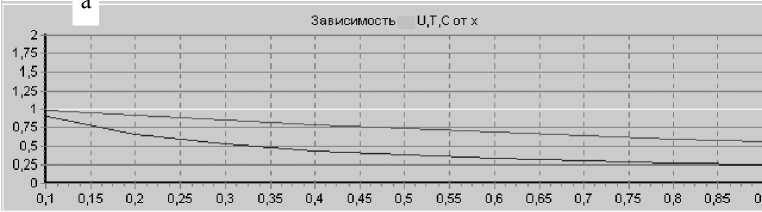
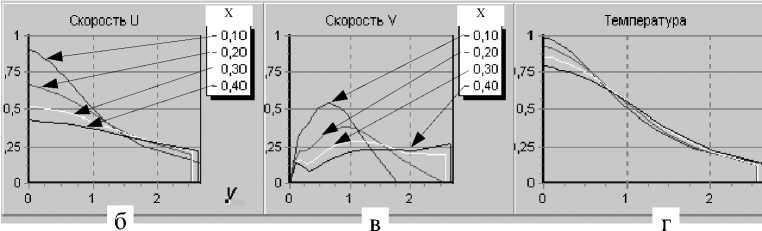
Рис. 1. Изменение продольной (U) и поперечной (V) компонент скорости смеси, избытка температуры (T) и концентрации пробы (C): а — вдоль оси капилляра; б, в, г — в поперечных сечениях (0.1, 0.2, 0.3, 0.4)

а

бвг

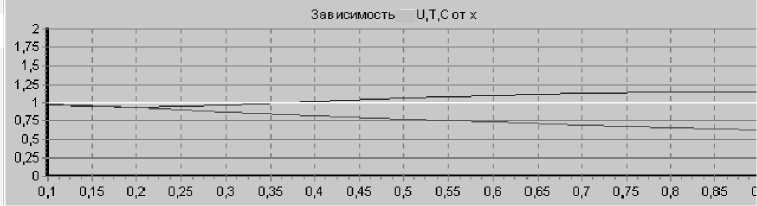
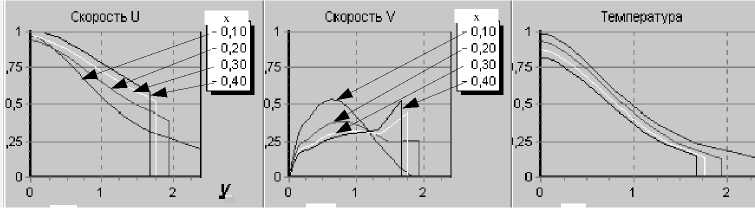
Рис. 2. Изменение продольной (U) и поперечной (V) компонент скорости смеси, избытка температуры (T) и концентрации пробы (C) при тепловыделении (Gr/Re =2): а — вдоль оси капилляра; б, в, г — в поперечных сечениях 0.1, 0.2, 0.3, 0.4

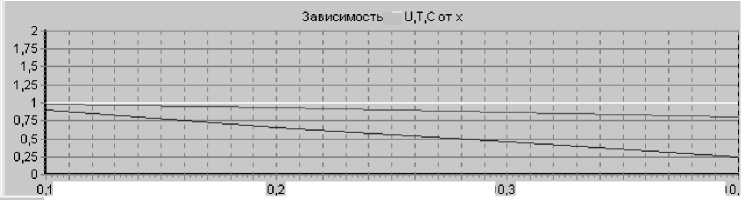
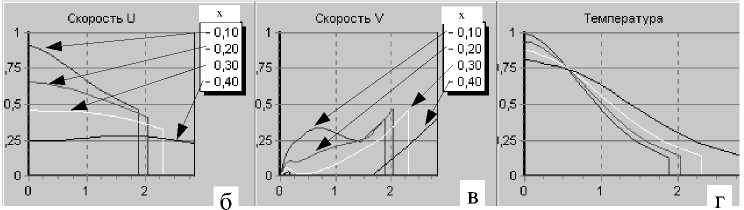
Рис. 3. Изменение продольной (U) и поперечной (V) компонент скорости смеси, избытка температуры (T) и концентрации пробы (C) при наличии частиц или с охлаждением (Gr/Re = – 0.5): а — вдоль оси капилляра; б, в, г — в поперечных сечениях 0.1, 0.2, 0.3, 0.4

u = 1, C = 1, A T = 1: 0 <  n <  1, £ = 0;

u = 0, C = 0, A T = 0: n = 1, £ = 0; d u   d C  dA T

7-              0 = v : n = 0; ^ >  0;

dn  on   on u = u G, C = 0, AT = 0: n = 1, ^ > 0-

Таким образом, решение задачи свелось к численному интегрированию уравнений (4–6)

с начальными и граничными условиями (7) в конечной полосе интегрирования по η от 0 до 1. Непосредственно численное интегрирование осуществляется методом прямых при равномерном разбиении полосы интегрирования ( ξ > 0, 0 ≤ η ≤ 1) на Р частей ( Р в расчетах варьировалось от 10 до 20).

На рис. 1–3 приведены результаты расчета полей продольной и поперечной компонент скоро- сти, концентрации пробы, избыточной ру ры в различных поперечных сечениях капилляра и вдоль его оси. Продольная скорость на границе 2-ой зоны (uG) полагалась равной нулю.

При отсутствии тепловыделения и при его наличии профили продольной скорости, температуры и концентрации быстро становятся пологими и выходят на автомодельный режим (на расстоянии порядка 0.4 диаметра капилляра); при охлаждении ситуация принципиально иная: продольная скорость быстро уменьшается вдоль оси капилляра, а профили характерных величин "помнят" начальные значения. Кроме того, в этом случае вдоль оси вблизи входа в капилляр поперечная скорость имеет значительные градиенты, что приводит к генерации возмущений в потоке.

Другой характерный вариант расчета течения в микроканале приведен ниже для плоской геометрии (рис. 4, 5).

Следует отметить, что при компьютерном моделировании течения в микроканале использовалось выражение для функции тока в уравнении движения

Ψ = cos h [ kh ( y – 1/2)]/ cos( kh /2),

Ψ — функция тока; k — величина, обратная длине Дебая; h — ширина канала.

Из рис. 4 видно, что наименьшие поперечные градиенты продольной скорости пробы при вводе в капилляр наблюдаются на расстоянии около 0.5– 0.6 (равенство скоростей на оси капилляра и около его поверхности).

На рис. 5 показано изменение продольной ком-поенты скорости ( U ) вдоль оси микроканала. Следует отметить, что учет электрических си дит к характерной перестройке профиля серповидной формы примерно с расстояния порядка 0.6 от входа в микроканал. В данном случае профили становятся фрактальными (афиноподобными), т. е. осуществляется выход на автомодельный режим.

ЗАКЛЮЧЕНИЕ

Анализ результатов компьютерного моделирования течения пробы с буфером с учетом ее ввода посредством электрического поля позволяет выбрать адекватную микрогидродинамическую модель и оптимальные области проведения концентрирования пробы и ее измерения.

Работа выполнена при поддержке грантов:

• 1.    Научная программа Санкт-Петербургского научного центра РАН "Аналитические приборы на основе микрофлюидных технологий" (раздел 2, проект 2, 2003 г.);

• 2.    Межведомственная    научно-техническая

программа "Вакцины нового поколения и диагно-

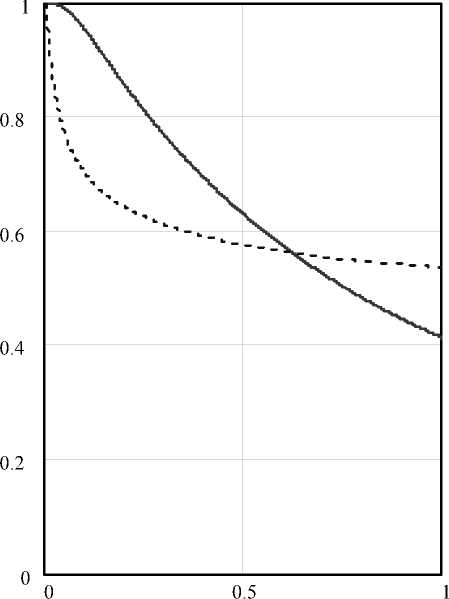
Рис. 4. Изменение продольной скорости смеси пробы с б уфером вдоль оси микроканала.

изменение скорости на оси микроканала, — — — вблизи поверхности микроканала

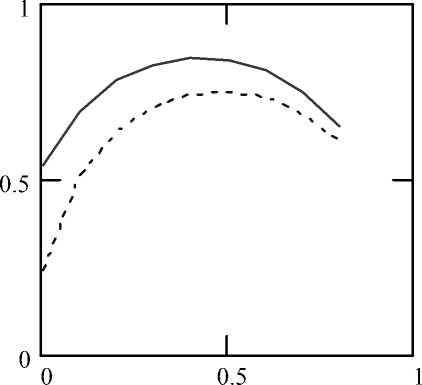
Рис. 5. Профили скорости смеси пробы с бу феро м вд оль оси микроканала на расстоянии

^_      0.1,

— — — 0.4

от входа в микроканал

стические системы будущего. Новые принципы детекции и разработка на их основе приборов для автоматизации лабораторно-диагностических методов исследования" (ГК N43.269.11.0206, 2002– 2006 гг.).