О комплексировании сейсмических и электромагнитных активных методов для картирования и мониторинга состояния двумерных неоднородностей в N-слойной среде
Автор: Хачай Ольга Александровна, Хачай Андрей Юрьевич
Статья в выпуске: 2 (219), 2011 года.
Бесплатный доступ
Даны анализ решения двумерной прямой задачи для сейсмического поля в динамическом варианте с использованием интегральных и интегродифференциальных уравнений, а также совместный анализ решений двумерных задач для переменного электромагнитного и сейсмического поля для моделей N-слойной среды с двумерными однородными включениями
Комплексная сейсмическая и электромагнитная методика, алгоритмы решения прямой динамической задачи сейсмики, совместный анализ прямых двумерных задач для сейсмического и электромагнитного поля, двумерная однородная неоднородность в n-слойной среде
Короткий адрес: https://sciup.org/147154732
IDR: 147154732 | УДК: 550.830+539.3
Текст научной статьи О комплексировании сейсмических и электромагнитных активных методов для картирования и мониторинга состояния двумерных неоднородностей в N-слойной среде
В связи с усложнением решаемых геологических задач все более актуальной становится проблема создания комплексных методик исследования. При комплексировании геофизических методов необходимо пространственное совмещение систем наблюдения и создание единых интерпретационных алгоритмов. В Институте геофизики УрО РАН разработана единая ЗО-методика наблюдений с использованием электромагнитных и сейсмических полей (в динамическом частотногеометрическом варианте), опирающаяся на единую концепцию трехэтапной интерпретации [10-13], которая включает в себя единую систему векторных наблюдений сейсмических и электромагнит ных полей. Используются локальные контролируемые источники возбуждения, для которых выполняются следующие условия: а) единая геометрия нормального поля, б) отсутствие одной или нескольких компонент в измеряемом поле в случае квазислоистой среды. Нами реализован вариант возбуждения электромагнитного поля вертикальным магнитным диполем и сейсмического поля вертикальной силой. Единый подход в интерпретации реализован для предварительно обработанных входных данных: сейсмические данные переводятся из временной области в частотную посредством преобразования Лапласа (для действительного параметра), а электромагнитные данные -
посредством преобразования Фурье (для действительной частоты) [И].
При проведении натурных экспериментов в рамках единой методики возникает возможность количественной оценки сопоставимости информации по различным полям о строении и физических свойствах среды, которая следует из критерия подобия систем наблюдений. В работе [8] изложены теоретические принципы построения такого критерия и алгоритмы его определения для нормальных полей в средах без включений.
В работе [4] изложена идея алгоритма построения критерия подобия для сейсмических и электромагнитных полей от сингулярных источников, эквивалентных проявлению искомого локального объекта в рассматриваемых полях. При этом объект в сейсмическом поле аппроксимируется погруженной точечной горизонтально действующей силой в W-слойном упругом изотропном полупространстве, в электромагнитном поле это погруженный горизонтальный магнитный диполь в TV-слойное изотропное проводящее полупространство. Выбор сингулярных источников определялся подобием морфологий создаваемых ими полей при взаимно перпендикулярном направлении моментов электромагнитного и сейсмического сингулярных источников. Разработан итерационный алгоритм вычисления электромагнитного и сейсмического полей при условии расположения аномальных источников в произвольном слое TV-слойной среды [5-7].
Настоящая работа посвящена выводу интегральных уравнений двумерной прямой задачи для сейсмического поля в динамическом варианте и совместному анализу интегральных уравнений двумерных задач для электромагнитного и сейсмического полей. Полученные результаты будут использованы для выбора критериев комплексиро-вания сейсмических и электромагнитных методов исследования сложно построенных сред.
1. Прямая динамическая задача сейсмики. Постановка задачи
Основное дифференциальное уравнение динамики упругого тела имеет вид [2]
_ - 82й yAu-v(X-vy?)graddivu + <5F0 = G——. (1)
8г
Здесь й(их,иу,и2) - вектор смещения; FQ(F0x,F0y,F0,') - вектор массовых сил; X и и - постоянные Ламэ; о - плотность среды; t - время.
Мы будем изучать сейсмическую задачу для случая установившихся колебаний [2]:
uAu + (X + y)graddiv'U + nF + or(2)
Введем обозначения:
* Х + Ц О 2 12
А = Дч--graddiv; — <о - к2 .(3)
Вц
Тогда уравнение (2) с учетом (3) можно переписать в виде
/Хйл-к2й =—F.(4)
В
Используя векторные преобразования [1], получим
(X + 2и) graddiv ы - yrotrotH + to2ей = -aF .
Представим и и F в виде:
й = gradtp + roly ; F = grad^ + rotW .(6)
Введем обозначения:
й] = grady. й2 = roty .
Тогда divu = divux = Аф; rotii = rotu2 =
= graddivy - Аф(7)
и graddivu = grad Аф; rotrotu = -rot Ay .
Внесем в (5) выражения (6), (8):
(X+ 2y) grad Ay+grot Аф+co2 agrady+
+ ygoroty = -G(gradФ + roW).(9)
Следовательно, чтобы удовлетворить (9), достаточно положить
(X + 2р)^гай?Дф+ ©2о§габ/ф = -agradФ;
grot Ay + со2 oroty = -ого^, или
(Х + 2ц)Дф + <в2аф =-пФ;
рАф + о2стф = -оФ.
Введем дополнительно обозначение:
С учетом (11) уравнения (10) можно записать в виде:
Дф + &2ф =---—Ф;
Х + 2р р
Будем предполагать, что среда является упругой и выполняется известная линейная зависи мость между компонентами тензора напряжений и деформаций [2]:
8и f 8и 8и А
=Xdivu + 2u. —-; т. =т, =р —-ч--— ;
-
х & Ау у' ( 8у дх )
су.. — Xdtvu + 2ц----* TY_ — Тту — ц-- 1--— 1 (13)
бу ( oz ах)
а. = Xdivii + 2р—-
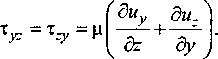
Воспользуемся приведенными в работе [2] наиболее часто употребляемыми граничными условиями: условиями закрепленной и свободной границы. В первом случае обращается в ноль вектор смещения на границе, во втором случае обращаются в ноль векторы напряжения, действующие на площадку границы с нормалью й.
Для системы уравнений (12) в [2] сформули рованы условия излучения в виде:
гйх = 0(1), ги2 = 0(1),
(6йх ]
г —--ikxux = о(1);
V 5г )
(8й2 )
Г -- --1К2иг = о(1).
V 8г )
-
2. Задача о дифракции звука на двумерной упругой неоднородности, расположенной ву-м слое TV-слойной среды
Рассмотрим более общую задачу дифракции звука на двумерной упругой неоднородности, расположенной в у-м слое Л'-слойной среды. Вывод соответствующих уравнений для задачи дифракции звука на двумерной упругой неоднородности, расположенной в упругом пространстве, сделан в работе [2].
Эту задачу будем решать, используя подход, изложенный в работе [3]. Массовые силы будем считать потенциальными и сосредоточенными в первом слое У-слойной среды. Плоскость ХОУ совпадает с верхней плоскостью 1-го слоя, z = 0. Ось 01 направлена вертикально вниз. Образующие двумерной неоднородности в виде цилиндра произвольного сечения направлены вдоль оси OY. Положим ц = 0, тогда в каждом из слоев выполняется первое уравнение из (12), преобразованное к виду:
Аф,+^Ф, = -2л/;(У0;
о (15)
w =
gradtp; j\
2лЛ, где / = 1,..., и; Ф, = Ф при z = 1, при / /1 Ф, = 0. Волновое число в z-м слое равно согласно (11):
Введем обозначение:
k^M^ = kXi - волновое число в слоистой среде;
.,У и
К^М^
кх р ч М € Sq , с
к(М), Mt So; J kjt
Индекс ji обозначает свойства среды внутри неоднородности, находящейся в пространстве с поверхностью So. В общем случае в произвольном слое или внутри неоднородности уравнение (15) с учетом (16) и (17) будет иметь вид:
^,+кЧМ)ц>х=-2^(М). (18)
Граничные условия в среде без разрывов, заключающиеся в непрерывности вектора смещения и тензора напряжений согласно (6) и (13) на границах раздела имеют вид:
5ф, 9Ф,+1 =0| .PM ■
8z 8z 'zs/‘’ ’ V 8n)jj \6n)/
[о,(го2Ф,+ Ф,)]-[ст,+1(<й2ф;+1 +ФМ)] = оЦ;
^а(со2ф + Ф)] =^о(ю2ср + ф/| ; (19)
|Ъ(®2ф+Ф)]|г=0 = О, где индекс ji обозначает значения о, ф, Ф на границе неоднородности с внутренней стороны, ja -с внешней стороны границы неоднородности, которая расположена ву-м слое; L - граница раздела слоя, с индексом i - со стороны z-ro слоя, с индексом z+1 -со стороны z+1-го слоя. Условия затухания на бесконечности согласно (6) и (14) имеют вид:
rgrad^j = 0(1), r(^- - г^ф,) = о(1). (20)
8г
Пусть
Ф,=Ф,-Ф^ (21)
где i = 1, ...J, ...,N; ф° - потенциал нормального сейсмического поля в слоистой среде в отсутствие неоднородности: ф“; = ф® и
5ф“ дф“+1 _0|
8z 8z lzeL-’ (23)
[о/ю^ + Ф;)]-[а,+1(ю2ф°+1 +Ф,+1)] = 0|гбА.. и о дф°
На контуре неоднородности ф и --- непрерыв-
8п ны. ф, - потенциал аномального сейсмического поля, который, с учетом (18), (17) и (21) удовлетворяет уравнению
Аф,- +
К2 (М
)ф, = -(У 2
(М) - к2
и граничным условиям:
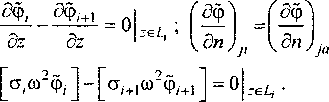
На контуре неоднородности
№v
Функция источника сейсмического поля GSp(.M,M°^ определяется решением следующей краевой задачи для У-слойной среды:
&GSpj+k2GSpj(M,M°) =-lid^M - М°) (27)
и граничным условием:
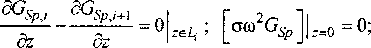
[<М%, ] - [CT,+i®2%/+i ] = о| 2eL, ■
На контуре неоднородности GSp^M ,М°^ и
8GS (М, М°)
——-----— непрерывны. Применим формулу
Эп
Грина [3] для функций ф, и GSp(.M,M°) для каждого слоя /V-слойной среды при i 4 j-
2л
Л+1
8GSP, г Вп
9GSp^x 3^>M ]J;
Я Gs ,+x — №+1 -
Bn Bn )
_ 2лфу(М°),М° eS,;
0, М° е Sj.
Приz =j
9GSp,j г 5Ф
Ц,
Вп Sp’J
^Gspj+x с
7+1
~™.....™" #GSpJ ^dc = о(М°ЖМ°). (33)
2л 4 Вп
Воспользуемся равенством [3]:
(^/о ji ) Г f 0 z » 9GSp,j .......' Ф ф(^)™™
2 л Вп
9GSp,j r Bn Spd
5фА
Вп
WJU =
_ 2лфДЛ/°), ЛГ° е S,;
0, М° й 8,-.
Помножим выражения (29) и (30) на
'(ova-GvV) 0(M0),
= i п (34)
О, M°£SC.
Тогда выражение (33) с учетом (34) можно переписать в виде: (к1 -к2 1
$WG^M,M°>hM +-^ФО(ЛГ°)-
271 Sc° Ji йр^=^^ ^ еs
2л Sp’J Вп
2 _ 2
^^~- JJ^^ J (M,M°)dTM +<р0(М°)-
о, и сложим
их с учетом граничных условий (28), в результате чего получим:
0Gsp,j
--Gs ——)dc =
2тг он on
о(М°)ф(Л/0), М° е Sj -Sc;
0, М° iSj-Sc.
Применим формулу Грина для функций GSpj(M,M0) для внутренности области учетом (25), (29), (31), (33) получим:
г2 _ I-2 2Jl^^M)Gsp^M,M0)dTM -
Ф/, и
8Г, с
, —de = ф(Л/0), 7И° « Sc.
о(Л/)2л^ Pd Вп 7 С
Таким образом, решив интегродифферен-циальное уравнение и определив распределение потенциала вектора упругих смещений внутри неоднородности, мы можем определить, используя второе интегро-дифференциальное представление, потенциал вектора упругих смещений в любом слое, затем используя соотношение (6), вычислить распределение вектора упругих смещений в любом слое.
1 r,~ 8GS , дф
""GsPj ~^dc =
2тс £, on on
^М°\ М° е8с; 0, М° 6 sc.
Помножим выражение (32) на av, и сложим с (32), с учетом граничных условий на контуре С неоднородности получим: ^AlAM ^M)GSp^M,M°)dTM +
2л ф 8п
3. Сопоставление алгоритмов для сейсмического (дифракция звука) и электромагнитного двумерного моделирования (Н-поляризация)
Сравним полученные выражения с решением задачи дифракции электромагнитного поля в рамках той же геометрической модели [3].
к1 -к2
Нх<м^=НАММАМ, M°)dTM +
2л "
а- vJ iHAM)—^dcA-^H^AM0), M° eSc;
k22n •( Bn k2L к2(к^Хк2 -к2Л
НАМ°Ж ---ГТ^^Я HAM)GAM,M°)dTM +
2^
k2(M°XkP -кЪ г BG „ „.
+---г—^— J-4>HAM)—dc+H°AM°), m°^sc.
к2к22и [. Вп
Здесь ^2(Л/°) = /<оц0о(Л/0), Цд = 4я-10 7™, о^М0) -м проводимость в точке Xf1; i - мнимая единица; НХ{М^) - суммарная составляющая магнитного поля; Н®(3/°) - составляющая магнитного поля слоистой среды в отсутствие неоднородности; k,, = z 1 6Gmi__Lf^+ll k2 дп k^ дп Сопоставим полученные уравнения для сейсмической и электромагнитной задачи: ^М°) = JJ W^M, M^dxM + +—---—®GSj—dc H-^-zp (M \М eSc; о.,2л • 4 дп о„' к2-!? Нх^) = \\Hx{M)Gm{M,M0)dxM + 2л у 1Л — к~ г^Ск^ -ААЦнX к2 2л дпк Различие в граничных условиях для сейсмической и электромагнитной задач приводит к различному типу уравнений: в сейсмическом случае -к интегродифференииальному уравнению, в электромагнитном случае - к нагруженному интегральному уравнению Фредгольма второго рода. Если при решении прямой электромагнитной и сейсмической задач в динамическом варианте удается установить подобие в явных выражениях для составляющих электромагнитного и сейсмического полей при определенных типах их возбуждения, то с усложнением структуры среды, как показывает полученный результат при анализе сейсмических данных, связанных с решением для продольных упругих колебаний, подобие исчезает. Это означает, что сейсмическая информация является дополнительной к электромагнитной информации о структуре и тем более о состоянии среды. 4. Алгоритм моделирования дифракции линейно поляризованной упругой поперечной волны на двумерной неоднородности, расположенной в j-м слое Л-слойной среды Рассмотрим задачу о дифракции линейно поляризованной упругой поперечной волны на дву мерной неоднородности, расположенной в j-м слое Л'-слойной среды, используя подход, описанный в работе [3] для электромагнитной двумерной задачи (случай Н-поляризации). Геометрическая модель среды аналогична описанной выше в предыдущей задаче. В этом случае в уравнении (5) Fv, F. равны нулю, и. = иу = 0, а составляющая вдоль оси ОХ не зависит от х. Составляющие тензора напряжения (13): . ди, ди, п х =о> =°_- =°;^ =°-(4°) ■ дуdz Тогда наша задача с учетом (8), сводится к решению следующей задачи: \их1+к2,их,=-2^М^ ^М)=^-Рх>,(41) где / = 1, ...,п; Fxi = F при /=1, при 1ф 1 Fxi =0. Волновое число в /-м слое равно согласно (3): ^2/ = А2 = Ю2 —.(42) И, Введем обозначение: к(М) = k2i - волновое число в слоистой среде, / = 1, ..., пи к^ ц 1 М е So; k(M-),M$S0-, (4э) Индекс ji, как и в предыдущей задаче указывает на свойства среды внутри неоднородности. В общем случае в произвольном слое или внутри неоднородности уравнение (41) с учетом (42) и (43) будет иметь вид ^х. +К2(М)иХ1 = -2к/,(М). (44) Граничные условия, заключающиеся в непрерывности вектора смещения и тензора напряжений на всех границах раздела, сводятся к непрерывно-ди„ D сти uxj и ц. ——. Выполнены условия затухания дп на бесконечности. Пусть йх,=их1-ихм (45) . о где z = 1, ...,j,ji, ..., п; uxj - составляющая нормального сейсмического поля в слоистой среде в отсутствие неоднородности: и^ = и® и \u°xiA-k2_A=-MW-, (46) P,^L-P,+I™!1 = o|^ ; U® -иА = оЦ • (47) dz dz ' 1 1 ' „ о Sw® На контуре неоднородности их и —- непре-дп рывны. йХ1 составляющая аномального сейсми- ческого поля, которая, как легко показать аналогично (24), удовлетворяет уравнению Ай„ +К\МК, = Ц^ШчР^Д (48) 2л / —- Ос. ; —_— ди ди dcJO Функцию источника сейсмического поля СЧ^М,М°) выберем следующим образом: она ц(Л/°)йг(М0), Мй eSj -Sc; a Hja “ Му - 0, M^Sj-Sc; Применим формулу Грина для функций GSsJ(M,M°) для внутренности области учетом (44), (46), (48), (50) получим: к2 -к2 dXJi и с dGSs j дйх ™дп GssJ~d^ de,, = определяется как решение следующей краевой задачи: и удовлетворяет граничным условиям: 8GSs,i 5Gs +1I Ц/ -Т— - И/+1 —Т---= 0 -ед ; ozoz ' Gs$ |z=o - 0; GSs j -GSs>l+1 - 0|,ед . На контуре неоднородности G4s(M,M°) и ——------ непрерывны. Применим формулу ди Грина [3] для функций й„ и GSs(M,M()) для каж дого слоя TV-слойной среды при i^j: 2кйх,(М°), М° е S,; 0, М0 г S,. При / =j 2miXJ(M°\M° eSj -Sc; 0, M° б5^8с. Помножим выражения (52) и (53) на р, и сложим их с учетом граничных условий (49) и (51), в результате чего получим: йх<М°\ М° eSc; 0, М° ^Sc. Помножим выражение (55) на ц/( и сложим с (54), с учетом граничных условий на контуре неоднородности получим: Sc ^■ja~ М-д) 1 O/izx^G&y , -- ---—Ф «“ (М )---—de + 2л ди + ^ ^G^ ^dc = ^М^мЧ (56) 2л £ ди Воспользуемся равенством [2] _^ - Нд ) г Г о(М)^2м _ G= 2л А диди ) ^-^(М0), М°eSc; =)(57) 0, M°$SC. Тогда выражение (56) с учетом (57) можно переписать в виде: 8С^Д ц^2п •’ ■ ди' 2 _ 2(58) Д Мх^., (М, M°)dTM +и°х(М°)+ ^(логл "- ц(М°)2л ^. 9п В выражениях (58) выписан алгоритм моделирования сейсмического поля для поперечных упругих колебаний в W-слойной среде, содержащей двумерную неоднородность. Первое выражение есть интегральное нагруженное уравнение Фредгольма второго рода, решением которого является распределение составляющей вектора упругих смещений для поперечных колебаний внутри неоднородности. Второе выражение есть интегральное представление для вычисления вектора упругих смещений в любом слое /V-слойной среды. 5. Сопоставление алгоритмов для сейсмического (линейно поляризованная поперечная упругая волна) и электромагнитного двумерного моделирования (Н-поляризация) Сопоставляя выражения (58) с соответствующими выражениями для электромагнитного поля (Н-поляризация) (36) мы видим наличие подобия интегральных структур этих выражений. Различие имеется в коэффициентах при соответствующих членах в выражениях (36) и (58), что можно учесть в выборе системы наблюдения того или иного поля. Следует учесть также различие в частотной зависимости отклика среды на сейсмическое и электромагнитное возбуждения. Однако при соблюдении коэффициентов подобия сейсмическое поле, возбуждаемое поперечными колебаниями, и электромагнитное поле будут содержать подобную информацию о структуре неоднородной среды и связанном с ней состоянии. Эти результаты подтверждаются натурными экспериментами, изложенными в работах [9, 12]. Заключение Предложен алгоритм решения прямой двумерной задачи для сейсмического поля в динамическом варианте при возбуждении источниками продольных и поперечных колебаний в виде интегро-дифференциального (в первом случае) и нагруженного интегрального уравнения Фредгольма второго рода (во втором случае) для решения внутренней задачи и соответствующих интегро-дифференциальных и интегральных представлений для решения внешней задачи. Произведено сопоставление полученных алгоритмов с алгоритмом решения прямой задачи для дифракции электромагнитного поля на двумерных неоднородностях, полученного В.И. Дмитриевым [3] (Н-поля-ризация). Показано, что для более сложных, чем горизонтально-слоистые структуры геологических сред, подобие электромагнитной задачи и сейсмической для продольных колебаний нарушается. Следовательно, эти наблюдения позволяют получить взаимно дополнительную информацию о структуре и тем более о состоянии среды. Эти поля различным образом отражают особенности неоднородных структур и реагируют на изменение их состояния. При возможности прослеживания сейсмических возмущений в виде колебаний толь ко сдвигового типа и наблюдений магнитной составляющей электромагнитного поля Н-поля-ризации в двумерной среде установлено их подобие, что может быть использовано при построении совместных систем наблюдения.
и граничным условиям:
Вйх; дйх ,+1
ц, И/+1 я =0
OZ OZ
Йх_, ~йх,М =0|.-еД “х\;
( 8й. А ( Эй.
1 SnJj, 1 SnJja
:=0 = 0’
ди°
(н7, нуо) я ;
ди
(49)
йх,р-йх,,а =0.
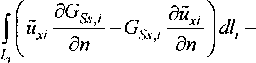
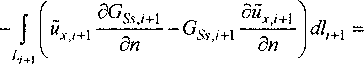
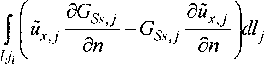
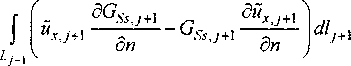
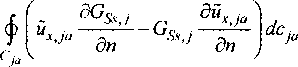
Список литературы О комплексировании сейсмических и электромагнитных активных методов для картирования и мониторинга состояния двумерных неоднородностей в N-слойной среде
- Кочин, Н.Е. Векторное исчисление и начала тензорного исчисления/Н.Е. Кочин. -М.: Изд-во АН СССР, 1951. -426 с.
- Купрадзе, В.Д. Граничные задачи теории колебаний и интегральные уравнения/В.Д. Купрадзе. -М.; Л.: Гос. изд-во технико-теоретической литературы, 1950. -280 с.
- Дмитриев, В.И. Дифракция плоского электромагнитного поля на цилиндрических телах, расположенных в слоистых средах/В.И. Дмитриев//Вычислительные методы и программирование в слоистых средах. -М.: Изд-во МГУ, 1965. -Вып. III. -С. 307-316.
- Хачай, А.Ю. Изучение критерия подобия сейсмических и электромагнитных полей от погруженных сингулярных источников для осуществления активного мониторинга нестационарной среды/А.Ю. Хачай//Глубинное строение, геодинамика, мониторинг. Тепловое поле Земли. Интерпретация геофизических полей: материалы Третьих науч. чтений Ю.П. Булашевича. -Институт геофизики УрО РАН, 2005. -С. 143-145.
- Хачай, А.Ю. Алгоритм решения прямой задачи электромагнитных исследований при возбуждении горизонтальным магнитным диполем, расположенным в произвольном слое п-слойной изотропной проводящей среды/А.Ю. Хачай//Информатика и математическое моделирование. -Екатеринбург, 2006. -С. 136-168.
- Хачай, А.Ю. Алгоритм решения прямой динамической задачи сейсмики при возбуждении горизонтальной точечной силой, расположенной в произвольном слое N-слойной упругой изотропной среды/А.Ю. Хачай//Информатика и математическое моделирование. -Екатеринбург, 2006. -С. 170-278.
- Хачай, А.Ю. Алгоритм решения прямой динамической задачи сейсмики при возбуждении точечным источником вертикальной силы, расположенной в произвольном слое N-слойной упругой изотропной среды/А.Ю. Хачай//Информатика и математическое моделирование. -Екатеринбург, 2006. -С. 279-310.
- Использование комплексной попланшетной сейсмической и электромагнитной методик для решения задач картирования приповерхностных неоднородностей/O.A. Хачай, B.C. Дружинин, Ю.С. Каретин и др.//Геофизика XXI столетия: 2001 г.: сб. тр. третьих геофизических чтений им. В.В. Федынского. -М.: Научный Мир, 2001. -С. 327-337.
- Хачай, O.A. Изучение критерия подобия для сейсмических и электромагнитных исследований в частотно-геометрическом варианте/O.A. Хачай, Т.А. Хинкина, В.В. Бодин//Астрономо-геодезические исследования. -Екатеринбург: УрГУ. -2001. -С. 30-35.
- Трехмерный электромагнитный мониторинг состояния массива горных пород/O.A. Хачай, Н.П. Влох, E.H. Новгородова и др.//Физика Земли. -2000. -№ 12. -С. 1-8.
- Хачай, O.A. Предпосылки сейсмоэлектромагнитного мониторинга нестационарной среды/O.A. Хачай, Т.А. Хинкина, В.В. Бодин//Российский геофизический журнал. -2000. -№ 17-18. -С. 83-89.
- Метод картирования зон потенциальной неустойчивости массива горных пород различного вещественного состава с использованием данных динамической сейсмики и электромагнитных индукционных исследований/O.A. Хачай, В.В. Бодин, E.H. Новгородова и др.//Горный информационно-аналитический бюллетень. -2001. -№ 3. -С. 10-16.
- Хачай, O.A. Исследование разрешающей способности попланшетной электромагнитной методики для активного картирования и мониторинга неоднородных геоэлектрических сред/O.A. Хачай, E.H. Новгородова, А.Ю. Хачай//Физика Земли. -2003. -№ 1. -С. 30-41.


