О конечном элементе на основе вариационного принципа Кастильяно для плоских задач теории упругости

Y.S. Sukhodolova, N.A. Trufanov

State National Research Polytechnic University of Perm, Perm, Russian Federation

ABOUT A FINITE ELEMENT BASEDON THE CASTIGLIANO VARIATIONAL PRINCIPLEFOR PLANE ELASTICITY PROBLEMS

We investigate the variant of the finite element method for plane elasticity problems, based on Castigliano variational principle. The quantitative characteristics of the convergence of the method on the example of solving the problem of tensile plate of variable load are resulted. We make recommendations for the implementation of the static boundary conditions in plane elasticity problems .

Keyword : finite element method, Castigliano variational principle, static boundary conditions.

Метод конечных элементов (МКЭ) представляет собой эффективный численный метод решения задач теории упругости [1–3]. Для построения конечно-элементных соотношений применяются различные вариационные формулировки, из которых наиболее широкое распространение получил подход, основанный на вариационном принципе Лагранжа – метод конечных элементов в перемещениях, согласно которому в качестве узловых неизвестных выбираются перемещения уз- лов элемента. В ряде случаев более удобным является использование метода конечных элементов в напряжениях, основанного на вариационном принципе Кастильяно [3]. Представляет интерес также развитие эффективных итерационных процедур решения краевых задач теории упругости, например метода геометрического погружения [4], а также его возможных конечно-элементных реализаций [4], в том числе с применением МКЭ в напряжениях [5].

Согласно вариационной постановке задачи теории упругости в напряжениях, основанной на принципе Кастильяно [6,7], решение ищется на множестве статически допустимых полей напряжений, удовлетворяющих статическим граничным условиям и уравнениям равновесия. Если в качестве узловых неизвестных при формулировке соотношений МКЭ выбрать компоненты тензора напряжений, удовлетворение уравнениям равновесия приведет к дополнительным условиям на неизвестные и значительному усложнению конечных соотношений. В случае плоской или осесимметричной задачи теории упругости удобна формулировка краевой задачи с использованием функции напряжений Эри [6], так как при этом автоматически удовлетворяются уравнение равновесия в каждой точке тела. Рассмотрим возможности МКЭ в напряжениях в терминах функции напряжений для плоской задачи теории упругости.

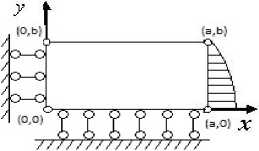
Рассматривается плоская задача теории упругости в декартовой системе координат об определении напряженного состояния прямоугольной пластины при продольном ее растяжении переменной распределенной нагрузкой (рис. 1). Поскольку задача симметрична относительно осей Ox и Oy , то для удобства будем рассматривать четверть пластины.

P ( y ) = 2o [ 1 - b^

Рис. 1. Расчетная схема поставленной задачи

Функционал дополнительной энергии упругой системы имеет вид

П- <*^) = 41?iIЕ°2 + °2 -2v°x°y + 2(’ + vK1dxdУ.°)

2E 00

Граничные условия задачи:

ux ( 0, У )= uy ( x,0) = 0,

/°xx ( a, У ) = P ( У ) ,

^T xy ( a , У ) = ^T xy ( ^x , b ) = ^T xy ( °, У ) = ^T xy ( ^x ,0 ) = ° yy ( ^x , b ) = °-

Поскольку известные из граничных условий перемещения на сторонах пластины нулевые, в (1) отсутствует интеграл, отражающий работу поверхностных сил на заданных перемещениях.

Связь функции напряжений Эри и компонент тензора напряжений имеет вид

5 ² ф      _ 5 ² ф      _ 5 ² ф

e y^’ ° ^yy =dx? , ^{T xy} =~^ y■

Тогда (1) примет вид ab

^П - ( ° )=^ ii

2E 00

'а ² ф? v^d y ² >

/ ^2   \ d ф v dx 2 v

- 2 v

'

v

а ² ф^л 'а ² ф^А a y ² Да x ² _v

+ 2 ( 1 + v )

f _я2 >

Vd x d y J

d x d y .

Для дискретизации функционала (5) выберем прямоугольный конечный элемент с четырьмя узлами в углах (рис. 2). Поскольку по форме задача для функции напряжений (бигармоническое уравнение) соответствует задаче об отыскании прогиба прямоугольной пластины, а возможные типы граничных условий в обеих задачах одинаковы (условия на искомые функции и их первые и вторые производные по координатам), разумно исследовать возможности конечных элементов, апробированных для задач изгиба пластин. Известны рекомендации [1, 3]

по применению прямоугольного конечного элемента с тремя неизвест- ными

{5J ⁷ =U ,

ap2 , ( 5») ^dx J i V dy J i

> в каждом узле. Однако в таком случае в

угловых точках элемента возникает противоречие, так как в них нельзя

52ф   д2ф обеспечить выполнение равенства ----=---- при произвольных зна- дx ду дx ду чениях узловых неизвестных элемента [8].

^ xx ( 0,0 ) , Па

А______

(1,1) —о

k

l

i

(0,0)

j

---о---►

(1,0) т xy ( 0,0 ) , Па

Рис. 2. Прямоугольный конечный элемент в локальной системе координат

Для преодоления этого затруднения примем смешанную произ водную

{ 5 _г } ^Г = k

в качестве одного из узловых   параметров:

^дфк ^5ф^ ^Л д ² ф^Л k dx J i ’ I dy h ’ I^d x ^д у J ,

Используя локальную систему координат, функцию напряжения Эри в элементе можно аппроксимировать выражением [8]

ф(Z,n) = Z(Nчф, + NЧ ^ + Nх ^ + N4 ^J = {N (Z.n)}" {«e}, (6) 7=7 k             дx ду дx ду J v             1 ’ где {Ne (Z, n)} — столбец функций форм элемента;

{ S e } = { S i , о j , о k , о , } - столбец узловых неизвестных элемента;

N 1 , = N , , ( Z ) N „ , ( n ) , N 2 , = N 0 , ( Z ) N 1 , ( n ) ;

N 3, = N , , ( Z ) N 0 , ( n ) , N « = N , , ( Z ) N ,, ( n ) ■

Функции формы N j в уравнениях (6) определяются как

N 0, ( Z ) = N 04 ( Z ) = 1 - 3 Z ² + 2Z³, N 0, ( n ) = N ы ( n ) = 1 - 3 n 2 + 2p²,

N 11 ( Z ) = N .4 ( Z ) = a ( Z- 2 Z’ + Z ³ ) , N 11 ( n ) = N .2 ( n ) = b ( n- 2 n ² + n ³ ) , N 0, ( Z ) = N „3 ( Z ) = 3 Z ² - 2 Z ³, N 04 ( n ) = N 03 ( n ) = 3 n ² - 2 n ³,

N 12 ( Z ) - N 13 ( £ ) -- a ( z ² -z ³ ) , N 14 ( n ) = N „( n ) = — b ( n 2 -П 3 ) .

Аппроксимирующая функция является неполным полиномом шестого порядка по Z и П (опущены сл а гаемые, содержащие степени выше третьих по любой переменной). При таком способе аппроксимации функция Эри и ее первые производные непрерывны вдоль сторон соседних элементов.

Используя связь функции напряжения Эри (4), введем следующее обозначение:

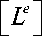
^ (Nel 5У 21 }

T

-^I Ne } 5 x² ’

T

5 у 5 x

IN}

T

4 5 ² b ² 5п 2

4 5 ²

a? TF

I Ne}}

I Ne}}

4 5 ²

ab 5Z5n

I Ne}}

где [ L e J - матрица градиентов конечного элемента для функции напряжений в случае плоской задачи. Таким образом, функционал (5) для конечного элемента примет вид

^П с - 5 II ( s e } [ LT [ D — ' J[ L U⁸ " ! d z d П= 0.

где I D ^{- 1} I - матрица констант упругой податливости:

: D "J- E

1 - v¹

- v ( 1 + v )

- v ( 1 + v )

1 - v ²

1 + v

в случае плоско-деформирован-

ного состояния;

[ D "J- E

- v

- v   0

0 1 + v

в случае плоско-напряженного состояния.

Согласно вариационному принципу Кастильяно требование ста- ционарности функционала дополнительной энергии

-5П.=0

5 I 8 }       '

где

Пс = ^ ПС , приведет нас к системе линейных алгебраических уравне-e ний [C]{3} = {^}, где {5} - глобальный столбец узловых неизвестных.

Основные трудности, возникающие при реализации данного варианта метода конечных элементов, заключаются в задании граничных условий в напряжениях. Граничные условия в перемещениях для данной вариационной формулировки являются естественными, и их учет труда не составляет. Выполнение главных статических граничных условий (3) может представлять собой достаточно сложную процедуру. Рассмотрим учет граничных условий на примере одной стороны элемента с узлами i и j , параллельной оси o y . В любой точке на этой

^{8 2} ^

стороне сxx = —-. Дважды интегрируя это выражение и определяя 5у константы интегрирования через ф и фy в узловых точках, получим yj

• -ф у +ф yj = Р xx ^d У ^, yi

yj y

• ^-ф _/ +ф ₇ .^- ф y b = Jj* G xx .

yiyi

Для учета таких линейных ограничений на узловые неизвестные была реализована попытка применения метода штрафных функций: введены штрафы к функционалу дополнительной энергии упругого тела за невыполнение заданных на границе условий в напряжениях. Исследованы возможные варианты выбора штрафных коэффициентов, при варьировании которых можно отслеживать выполнение статических граничных условий на каждой грани. В качестве второго способа было опробовано решение методом наименьших квадратов переопределенной системы, включающей исходную СЛАУ, дополненную записанными граничными условиями на узловые неизвестные. Применение обоих способов дает неудовлетворительное качество численного решения.

Качественное решение обеспечивается в случае задания в граничных узловых точках элементов значений как самой функции напряжений Эри, так и ее первых производных с помощью модификации глобальной матрицы податливости. Для этого необходимо проинтег- рировать по внешним границам элементов заданные условия в напря- жениях (вычислить интегралы вида:

yy

f ( У ) = j o xx d у , g ( y ) = j f ( y ) d y .).

Для сравнительного анализа результатов поставленная задача решена тремя способами:

• 1)    МКЭ, основанным на вариационном принципе Кастильяно;

• 2)    МКЭ, основанным на вариационном принципе Лагранжа (четырехугольный билинейный элемент);

• 3)    путем прямой минимизации функционала дополнительной энергии упругого тела методом Ритца [9].

Для получения приближенного аналитического решения методом Ритца была выбрана аппроксимация решения на основе базисной функции вида

* = 2 Sy ²

f 1 - 1 y )

I ⁶ b ² )

+ ( x x

- a ² ) ( yx - b ² ) ( a , + a ₂ xx +a ₃ y ² ) ,

где a , , a ₂, a ₃ - неизвестные постоянные, S = 20.

Подставляя все в функционал (5) и дифференцируя по неизвестным постоянным коэффициентам, придем к линейным уравнениям относительно a , , a ₂ , a ₃, получим следующее их значение:

S             S              S

• a, = 0,07983, a₂ = 0,1250- S -, a₃ = 0,01826- S- .

• ¹               a ⁴ b ^{2     2}             a ⁶ b ^{2     3}               a ⁶ b ²

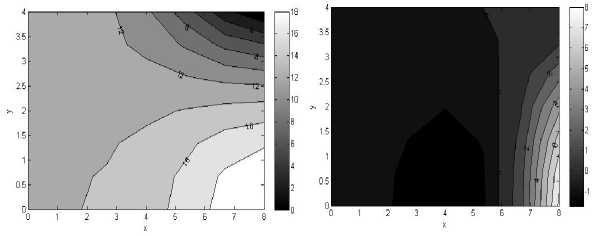
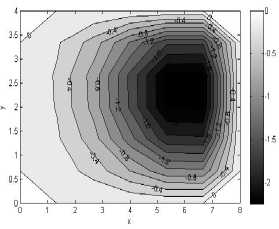
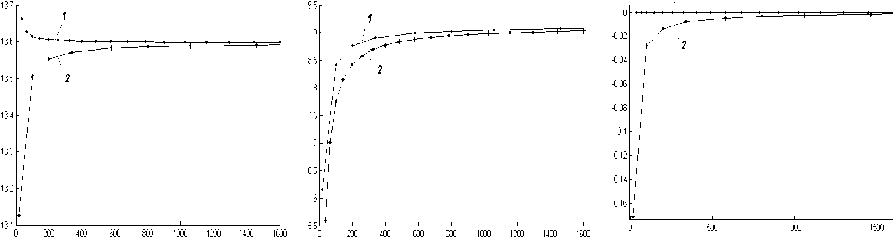
Приближенное решение задачи представлено на рис. 3. На рис. 4 представлены результаты, полученные методом конечных элементов в напряжениях на сетке 10 x 10 узлов. Для сравнительного анализа метода конечных элементов в формулировках Лагранжа и Кастильяно представлено изменение напряжений в конкретных точках пластины в зависимости от числа узловых неизвестных в конечно-элементных сетках (рис. 5). МКЭ в формулировке Кастильяно при определении напряжений имеет значительно более высокую скорость сходимости.

Известно, что в случае плоско-деформированного состояния реализация метода конечных элементов в перемещениях испытывает значительные затруднения для слабосжимаемых изотропных материалов, а для несжимаемых материалов в традиционной формулировке решение невозможно.

а

б

в

а

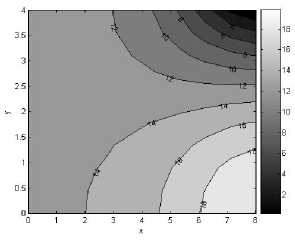
Рис. 3. Приближенное аналитическое решение задачи. Изолинии равных значений напряжений: а - ст xx , Па , б - ст _yy , Па , в - т _xy , Па

б

в

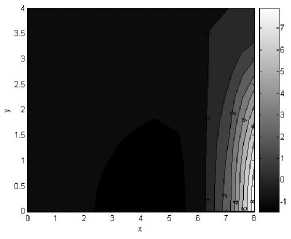
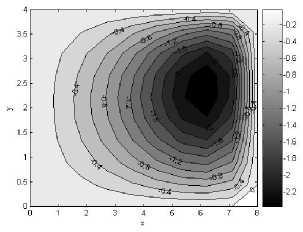
Рис. 4. Решение методом конечных элементов в напряжениях. Изолинии равных значений напряжений: а - ст xx , Па , б - ст _yy , Па , в - т xy , Па

^ст yy ( 0,0 ) ,^Па                    ст xx ( 0,0 ) , Па                    ^т xy ( 0,0 ) ,^Па

а       N           б       N

N

Рис. 5. Изменение напряжений с увеличением числа степеней свободы в конечноэлементном аналоге: 1 – решение на основе вариационного принципа Кастильяно, 2 - решение на основе вариационного принципа Лагранжа; а - ст xx ( 0,0 ) , Па , б - ст yy ( a ,0 ) ,Па , в - т xy ( 0,0 ) ,Па

Для формулировки в напряжениях эти ограничения отсутствуют. Рассмотрим результаты применения МКЭ в напряжениях к решению задачи о поперечном сжатии переменной распределенной нагрузкой изотропного бруса с коэффициентом Пуассона, равным 0,5: левая грань бруса закреплена жестко, на правой грани приложена параболи- ческая сжимающая нагрузка, верхняя и нижняя грани свободны от нагрузок. На рис.6 представлены графики сходимости решения по нормальным напряжениям: изображены напряжения в центральной точке пластины в зависимости от числа узловых неизвестных. Решение практически сходится при 1600 степеней свободы, что соответствует конечно-элементной сетке 20 х 20 узлов.

о „ ( 0,0 ) , Па

^g yy ( 0,0 ) ,Па

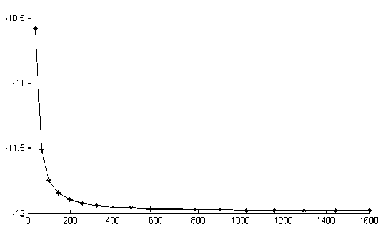
а            N                 б            N

Рис. 6. Изменение напряжений с увеличением числа степеней свободы. Решение методом конечных элементов в напряжениях: а - о xx ( 0,0 ) , Па , б - g yy ( 0,0 ) , Па

Таким образом, применение метода конечных элементов на основе вариационного принципа Кастильяно позволяет получать хорошие численные результаты по определению полей напряжений на сетках достаточно низкой размерности, в том числе для несжимаемых материалов. Такие формулировки имеют определенные сложности при построении криволинейных элементов. Преодоление данных затруднений возможно в рамках реализации общей процедуры метода геометрического погружения на основе вариационного принципа Кастильяно [4, 5].