О конвективных вихрях Карига в палеозойском мантийном клине под Тимано-Печорской плитой как механизме выноса углеводородов

Тимано-Печорская плита на западе и юго-западе ограничена складчатыми сооружениями Тиманского кряжа, а на востоке и северо-востоке — Уралом и Пай-Хоем. Геофизическими методами устанавливается северная граница провинции, проходящая по субширотному глубинному разлому приблизительно в 50 км к северу от о. Колгуев в Баренцевом море. В рельефе плиты выделяется ряд параллельных Тиманскому кряжу крупных впадин (Ижма-Печорская, Денисовская, Хорейверская, Коро-таихинская, Косью-Роговская), разделенных региональными поднятиями (Восточно-Тиманский и Печоро-Кол-винский мегавалы, Шапкино-Юрьяхинский, Лайский, Колвинский, Варандейский валы, вал Сорокина). Отмечается, что с валами связаны основные нефтегазоносные зоны [6]. Вытянутые параллельно юго-западной границе Тимано-Печорской плиты чередующиеся зоны топографических поднятий и депрессий и подобным образом вы- тянутые периодически чередующиеся аномалии плотности [1] свидетельствуют, что своим происхождением эти структуры могут быть обязаны 2D-конвекции в мантийном клине, образовавшемся при закрытии в палеозое Палеоуральского океана, и связанной с этим процессом суб-дукцией Русской плиты под Тимано-Печорскую. После закрытия океана в конце палеозоя субдукция прекратилась [9]. Однако и в наше время наблюдаемая на профиле «Кварц» наклонная зона повышенных сейсмических скоростей в мантии на глубинах ~ 50—100 км, падающая в восточном направлении под углом ~ 8—9° [8], вероятно, свидетельствует, что субдукция Русской плиты под Тимано-Печорскую действительно имела место и наклонная зона повышенной плотности является остаточным фрагментом Русской плиты, субдуцировавшей под Тимано-Печорскую в палеозое. Впоследствии вариации рельефа, возникшие вследствие горизонтальных изменений температуры в мантийном клине, охваченном 2D-конвек- цией, сохранились до настоящего времени, поскольку, согласно исследованиям [14], именно благодаря конвекции в мантийном клине и связанному с ней переносу базальтовой магмы происходит процесс роста коры на литосферной плите над субдуцирующим блоком. Следует отметить, что мелкомасштабная конвекция, исследуемая в настоящей работе, возникает при весьма специфических условиях (крайне малый угол и достаточно большая скорость субдукции) и не исследовалась ни в статье Т. В. Геруа [14], ни в цитируемых там работах, где рассматривались химико-плотностная конвекция, а также конвекция в виде плюмов и валов, ориентированных в направлении субдукции. Нефтегазоносные зоны на Тимано-Печорской плите также вытянуты параллельно Тиман-скому кряжу, приурочены к топографическим поднятиям и, возможно, тоже связаны с конвективными потоками, восходящими в мантийном клине и выносившими нефть мантийного (как отмечается в работе [7]) происхождения. Предполагая, что размер 2П-конвективной ячейки Карига термической мантийной конвекции равен длине волны вариаций рельефа, можно, как уже было предложено ранее [2], оценить среднюю скорость субдукции Русской платформы при закрытии Палеоуральского океана (~ 5—6 см/год). Эта скорость получается из предположения о постоянстве вязкости в мантийном клине, и в настоящей работе представляется важным рассчитать характерные масштаб и локализацию конвективной неустойчивости для более реалистического реологического закона, учитывающего эффекты фазовых переходов и зависимость коэффициента вязкости от температуры и давления, и, как следствие, уточнить оценку скорости субдукции. Коэффициент вязкости в мантийном клине, вероятно, очень мал, порядка 1018 Па-с и менее, что связано с наличием воды, поднимающейся в мантийный клин из субдуцирующего блока [5]. Как отмечается [11], добавление 102—103 г воды на тонну оливина уменьшает вязкость на два порядка по сравнению с условиями отсутствия воды в горной породе. В предлагаемой модели понижение вязкости из-за присутствия воды учитывается усредненно путем использования реологических параметров «влажного» оливина.

Методы и подходы

В качестве модели термомеханического состояния мантийного клина между подошвой Тимано-Печорской плиты и поверхностью Русской плиты, пододвигающей Тимано-Печорскую под углом в со скоростью V, примем модель, получаемую при Pr ^~ в приближении Буссинеска из системы двумерных безразмерных уравнений гидродинамики для функции тока у и температуры T [14]:

2     -2 . ..2     -2 .       ..2 .2

^(d zz ^{- d} xx ) n ^(d zz -8 xx ) y + 48 xz n S xz v =

= RaT - Ra ⁽⁴¹⁰⁾Г⁽⁴¹⁰⁾ - Ra ⁽⁶⁶⁰⁾r < ⁶⁶⁰⁾ ,        (1)

xx   x

Di т ²

8 T = A T - у Tx + V T₇ + — х -ik" + Q . t         v z x v x z Ra ₂n

Здесь n — безразмерный коэффициент динамической вязкости, символ д и индексы означают частные производные по координатамx (горизонтальной), z (вертикальной) и времени t, А — оператор Лапласа, Г(410) и г(660) — объемные доли тяжелой фазы на фазовых переходах на глуби нах 410 и 660 км, компоненты скорости Vx и Vz связаны с функцией тока как

V x = V x . V. = - V x .                  (3)

а безразмерные числа Рэлея Ra, фазовые Ra(4100, Ra(660) и диссипативное Di есть аР gd 3T         8

Ra = —₌—¹ = 5.55 х 10 , ηχ

, (410) ,3

Ra(410) = бр  gd = 6.6 х108 ηχ s (660) ,3

Ra ⁶⁰ = ^бр    ’gd = 8.5 Хю ⁸

ηχ

Di = ^g d = 0.165,                   (4)

cp где а = 3х10-5 K1 — коэффициент теплового расширения, p = 3.3 г-см-3 — плотность мантии, g — ускорение силы тяжести, cp = 1.2х103 Дж-кг-1-К-1 — удельная теплоемкость при постоянном давлении, T(= 1950 К — температура основания переходной зоны мантии (ПЗМ) на глубине 660 км, считающейся нижней границей модельной области, Q = 6.25х10-4 мВт.м-3 — объемная мощность тепловыделения в коре, тik — тензор вязких напряжений, d = 660 км — вертикальный размер модельной области, П = 1018 Па.с — масштабный множитель вязкости, х = = 10-2 см2. с-1 — коэффициент температуропроводности, 6p(410) = 0.07p и 5p(660) = 0.09p — скачки плотности на фазовых переходах на глубинах 410 и 660 км. В (1), (2) масштабными множителями для времени t, напряжений тik и функции тока у служат соответственно величины d2-x-1, Пx2-d-2 и х. Предполагая реологию линейной для диффузионного механизма ползучести, доминирующего в мантии на глубинах более ~ 200 км [11], примем зависимость коэффициента вязкости n от температуры Tи литостатического давленияp в виде [5]:

/ X m *      *

р | h | E + pV

П = I I exp

2 A ( b * J        RT

,

где для «влажного» оливина A = 5.3 х 10¹⁵ с ^-1, m = 2.5, размер зерна h = 10^-2 — 1 см, вектор Бюргерса b * = 5 х 10^-7 мм [4], энергия активации E = 240 кДж ^. моль^-1, объем активации V = 5 см^{3 .} моль^-1, ц = 300 ГПа — нормирующее значение модуля сдвига, R — универсальная газовая постоянная. При этих значениях констант, выбранном масштабном множителе П = 10¹⁸ Па ^. с и размере зерна h = 10^-2 см безразмерный коэффициент вязкости, который также обозначим через n , равен:

14.8 +1.34(1 - z )

- „ . „-7

П = 5.0 х10 exp

T

где T — безразмерная температура, а безразмерная координата z , нормированная на d , отсчитывается вверх от основания ПЗМ (ось x направлена по нижней границе ПЗМ против субдукции). Отношение сторон модельной области примем равным 1:6, так что при субдукции по диагонали модельной области угол субдукции составит в = 9°, а принятая в расчетах скорость V = 6 смтод^-1 в единицах x ²'d^-1 равна V = 1.25 х 10³, т. е. в субдуцирующей плите ее компоненты V_x = —1.233 х 10³ и V z = -0.164 х 10³.

Следуя авторам [10], примем фазовые функции Г ( ¹⁾ в виде (напомним, что ось z здесь направлена вверх, поэтому знаки изменены):

г ( ' ) 1 fi z- - z ⁽ ' ) T ))

^Г = 2 ¹ - th ----( I T” ,

• ²    ^ w J

7 ^{( 1 )}(T}—7⁽¹ ) —__ ( T T^{( 1} )

z ^{( T} ) - z 0-- ^{( T -} T 0 ) ,               (7)

ρg где z(!)( 1) — глубина 1-го фазового перехода, z0') и T0') — усредненные глубина и температура фазового перехода, Y(410) = 3 МПа-K-1 и Y(660) = —3 МПа-K-1 — наклоны кривых фазового равновесия, w(1) — характерная ширина 1-го фазового перехода T(410) =1800 K, T3(660) = 1950 K — средние температуры фазовых переходов. Теплоты фазовых переходов [9], в (2) не учитываются ввиду несущественности в случае развитой конвекции. Из (7) получаем:

г(1)      ^) сГ2 z-z0') + Y( ' \T-T0( '))/Pg x = " 2pgw(1)                  w(')

x T_x

откуда видно, что фазовый переход с Y^ > 0 усиливает конвекцию (при 1 = 410), а фазовый переход с Y *) < 0 (при 1 = 660) — ослабляет. В безразмерном виде z 04 ¹⁰⁾ = 0.38, z 0 ⁶⁶⁰⁾ = 0, w ⁽ h = 0.05, У⁴¹⁰⁾ = 2.55 х 10⁹, У⁶⁶⁰⁾ = —2.55 х 10⁹, T ₀ ⁽⁴¹⁰⁾ = 0.92, T ₀ ⁽⁶⁶⁰⁾ = 1, и в (1):

х ( 1 )       ( 1 )

( 1 ) ₌ ⁵P Y _v

Г x         в (1) о (') Х р Ra 2 w z - z О!1 + 71'1 ^ (T - T())

Х ch"²------------- P R a ------------x T x .       (9)

w

В качестве граничных условий приняты изотермич-ность горизонтальных и адиабатичность вертикальных границ, условия прилипания и непроницаемости границ (кроме «окон» внедрения и выхода субдуцирующей плиты, в которых задана скорость субдукции и проницаемости удаленной от зоны субдукции границы под прямым углом, близким к углу выхода вынужденного мантийного потока при пологой субдукции). Величина Q в (2) отлична от нуля в континентальной и океанической коре мощностью 40 и 7 км соответственно. Начальная температура вертикальных границ принята по модели охлаждения полупространства в течение 1 млрд лет для Тима-но-Печорской плиты и 100 млн лет для Русской плиты. Безразмерное т^ в (2) удобно выразить через у как тk = 4n2[(Vzz -Vxx)2/2 + 2VXz].          (10)

Результаты и обсуждение

Для построения согласованной модели мелкомасштабной термической конвекции в мантийном клине между настилающей Тимано-Печорской плитой и субдуцирующей Русской плитой, ради повышения точности вычислений вначале необходимо положить в (1) — (2) Ra ^ 0, Di = 0, т. е. рассчитать модель погружающейся плиты, мантийного клина и настилающей плиты без учета вязкой диссипации и конвекции. Это связано в тем, что при Ra и Di (4) конвекция проходит стадии с большими скоростями, и для обеспечения устойчивости расчета требуются крайне малые шаги по времени. Полагая вначале в (1) — (2) Ra ^ 0, Di = 0, т. е. учитывая только теплопроводность и адвекцию тепла и интегрируя (1) — (2) по пространственным координатам методом конечных элементов на сетке 104 х 104 и по временнуй координате методом Рунге — Кутта 3-го порядка, получим квазистационарные безразмерные у и T = T_R, изображенные на рис. 1 и 2, где линии тока на рис. 1 показаны с интервалом 0.25, а изотермы на рис. 2 — с интервалом 0.05 (вертикальная шкала на рисунках растянута в два раза). Плита, субдуцирующая с заданной скоростью V , считалась жесткой, а коэффициент вязкости в зоне трения литосферных плит при температурах ниже 1200 K понижался по сравнению с (5) на два порядка величины. Последним учтен эффект смазки за счет субду-цирующих осадков, которые частично затягиваются погружающейся плитой и препятствуют прилипанию к ней настилающей литосферы [13]. Полагая затем безразмерные параметры в (1) — (2) согласно (4), то есть включая эффекты диссипации и конвекции, и интегрируя (1) — (2), находим, что показанный отрицательными линиями тока на рис. 1

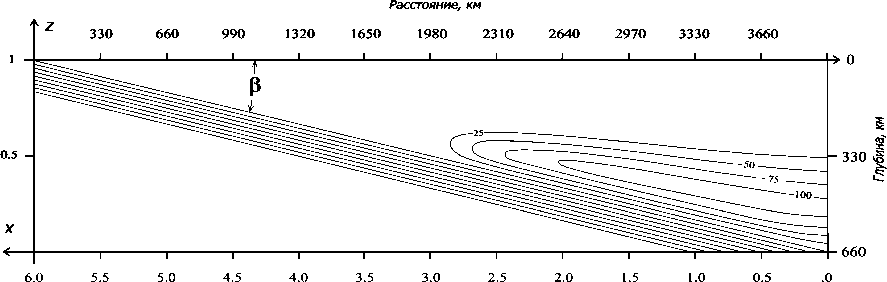
Рис. 1. Квазистационарное распределение безразмерной функции тока в области субдукции Русской плиты под Тимано-Печорскую без учета эффектов диссипативного нагрева и конвекции. Параллельные эквидистантные линии тока соответствуют субдуцирующей Русской плите, линии тока с отрицательными значениями у — вынужденному движению, вызванному субдукцией

Ris. 1. Quasi steady-state non-dimensional streamfunction in the zone of subduction of the Russian plate under the Timan-Pechora plate at Peleozoic with no effects of dissipative heating and small scale convection. Parallel equidistant streamlines represent subducting Russian plate, streamlines with negative у correspond to mantle flow induced by subduction

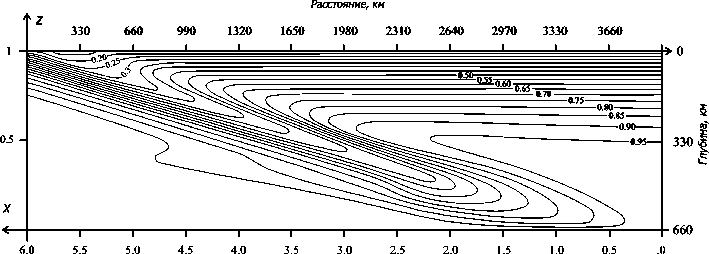
Рис. 2. Квазистационарное распределение безразмерной температуры в мантийном клине без учета эффектов диссипативного нагрева и конвективной неустойчивости

Ris. 2. Quasi steady-state non-dimensional temperature in the mantle wedge with no effects of dissipative heating and small scale convective instability

вынужденный мантийный поток в мантийном клине за время ~ 1.5 х 10^-4 (в размерном виде ~ 1.3 млн лет) частично разрушается конвекцией, которая по достижении квази-стационарного режима принимает вид, изображенный на рис. 3 вихревыми линиями тока с интервалом 0.25. На рис. 3 видно, что масштаб конвективных ячеек Карига — порядка 300 км, а густота линий тока соответствует скорости конвективных движений менее или порядка 10 см-год^-1. В верхней части рис. 3 показаны связанные с конвекцией изостатические вариации рельефа, вычисленные по формуле:

h = a dT 1 ^{P m} f ( T - T R )dz ,             (11)

^P c 0

где переменные под знаком интеграла безразмерны (TR — температура, показанная на рис. 2), а рm и рc — плотности мантии и коры. Видно, что вариации рельефа составляют несколько сотен метров, и топографические поднятия располагаются над восходящими конвективными потоками, показанными стрелками a, b, c и d. Характерный размер конвективных ячеек (вихрей Карига) порядка пространствен ного периода расположения топографических поднятий в рассматриваемом регионе (~ 300 км), а горизонтальная протяженность AB конвективной зоны та же, что у всей Тима-но-Печорской нефтегазоносной провинции (~ 1300 км). Это дает основание утверждать, что в рамках модели с реалистической реологией мантии, учитывающей влияние фазовых переходов и зависимость вязкости от температуры и давления для «влажного» оливина, скорость субдукции Русской плиты под Тимано-Печорскую может быть оценена в ~ 6 смтод-1. Отметим, что образование в мантийном клине конвективных валов, ориентированных поперек субдукции, как на рис. 3, характерно для малых углов субдукции и уже при в = 30° поперечные валы не возникают [3,14]. При рассмотренном угле субдукции в = 9° конвекция не возникает при скорости V< 5 смтод-1. Очевидно, наличие двумерной конвекции в узком мантийном клине связано с бульшими, чем в широком клине, вязкими напряжениями и, следовательно, с бульшим диссипативным нагревом. Следует отметить, что в многочисленных исследованиях термомеханического состояния мантии в зонах субдукции (см., например, [13, 14] и обширную библиографию в этих статьях) не

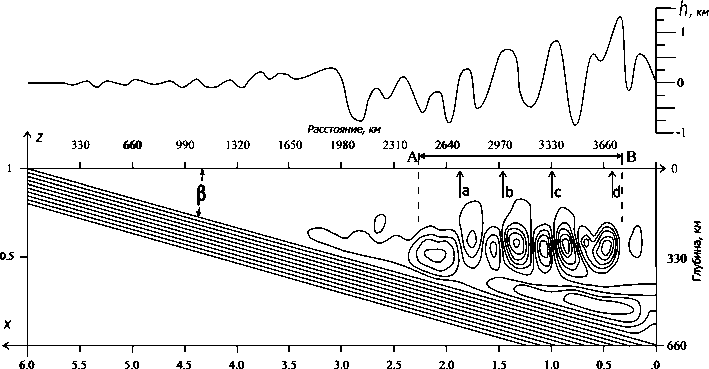
Рис. 3. Квазистационарное распределение безразмерной функции тока над нижней границей переходной зоны мантии с учетом диссипативного нагрева, конвективной неустойчивости и фазовых переходов. Вихревые линии тока соответствуют конвективным движениям (вихрям Карига), которые могут обеспечить вынос мантийных углеводородов к дневной поверхности вдоль линий a , b , c, d . AB — общая горизонтальная протяженность зоны с развитой конвекцией в мантийном клине. В верхней части рисунка изображены изостатические вариации рельефа, вызванные конвекцией

Ris. 3. Quasi steady-state non-dimensional streamfunction above the lower boundary of mantle transition zone with dissipative heating, convective instability and phase transitions. Vortices correspond to convective flows (Karig rolls) possibly providing vertical transport of mantle hydrocarbons to the Earth’s surface along the directions a , b , c, d

получалось конвекции в виде валов, поперечных к направлению субдукции, так как модели с крайне малыми углами субдукции не рассматривались.

Выводы

Характерный масштаб конвективных ячеек, полученных для реалистической реологии мантийного клина, сформировавшегося в палеозое в ходе закрытия Палеоуральского океана и субдукции Русской плиты под Тима-но-Печорскую, составляет ~ 300 км, что приблизительно совпадает с характерным пространственным периодом расположения топографических поднятий в Тимано-Печор-ском регионе. Горизонтальная протяженность всей Тима-но-Печорской нефтегазоносной провинции, в которой зоны нефтегазонакопления приурочены к поднятиям рельефа, совпадает с горизонтальной протяженностью зоны, в которой развивается конвекция. Скорость движения в конвективных вихрях может достигать десятка сантиметров в год, что, по-видимому, может обеспечить достаточно эффективный вынос базальтовой выплавки к дневной поверхности и формированию рельефа коры. Совпадение порядков величины конвективных ячеек и пространственного масштаба периодичности нефтегазоносных зон, приуроченных к топографическим поднятиям, служит подтверждением оценки скорости субдукции Русской плиты под Тимано-Печорскую в палеозое (~ 6 смтод-1).