О математических принципах построения областей виброизоляции

Основной из актуальных задач при проектировании систем управления является проблема корректного сопряжения генератора как источника питания и исполнительных органов. При этом привод от источника питания к исполнительной части устройства должен, кроме того, сглаживать вибрации от генератора, которые искажают требуемую динамику движения исполнительных органов. Решение этой проблемы является задачей виброизоляции или виброзащищенности пространства состояний исполнительной части устройства. В случае представления задач в виде линейных систем дифференциальных уравнений, решение проблемы опирается на принцип суперпозиции математической модели свободного движения управляющего объекта и управления с обратной связью. В случае нелинейного регулятора принцип суперпозиции решений, как известно, неприменим [2]. Колебательные системы с неидеальным источником энергии можно представлять как систему автономных динамических систем, содержащих подсистемы источника питания, связанных с колебательными системами, вообще говоря, нелинейными обратными связями по полному вектору состояния всей системы в целом. Термин «неидеальный источник» обязан своим происхождением именно формированию контуров нелинейных обратных связей между колебательными подсистемами и источником энергии. При этом поведение колебательных подсистем влияет на динамические характеристики источника. В свою очередь изменение характеристик источника питания влияет на поведение колебательных подсистем.

В данной статье подход к виброизоляции опирается на теорию устойчивости инвариантных множеств, построенной В.И. Зубовым [3].

Схема синтеза

Введем функцию F(xi,x2,™,x2n), повер- хности уровня которой являются односвязными и замкнутыми. Следуя работе [там же], запишем условие инвариантности для одной из поверхностей уровня функции F(x1,x2,...,x2n): ^L^дт + x2i lx--j(F(x))= ф(x)(С - F(x)), тогДа и только тогда, когда x = (x1, x2, „., x2n) удовлетворяет уравнению F (x) = C .

При этом, если положить, что n

^ ( x ) = E P 2 x 2 22 , где P ₂ i >  0 - константы и i = 1

F (x) определенно положительна, то и ее полная производная на движениях системы в области Q1 = {x e R2n | F(x) < C} будет определенно положительной функцией, в области П2 = {x e R2n | F(x) > C} — определенно отрицательной , то есть F (x) – функция Ляпунова. Так как поверхность уровня F (x) = С, помимо всего прочего, является инвариантной, то при выполнении условий существования решений задачи Коши и их единственности следует, что траектории, лежащие внутри области фазового пространства, ограниченной этой поверхностью, и вне нее, не могут ее пересекать.

Если данная схема синтеза удовлетворяет теоремам Зубова [3], то задача синтеза имеет положительное решение.

1. Постановка задачи стабилизации произвольного числа свободных апериодических движений

Рассмотрим следующую задачу:

Y ■ Q Y + AY + U ( Y , Y ) = 0 , y n - ^а У n ⁺ « n У п ⁺ u n ( ^{Y , Y} ) = 0,

Теорема [1]. Пусть будут выполнены условия: 1) система состоит из неидеального источника питания и n – 1 двойных апериодических звеньев; 2) коэффициенты U управления с обратной связью по вектору состояния системы ( ) удовлетворяют следующим соотношениям: а) коэффициенты внутриконтур-ного управления: p2,-2i—1 = a, в2i,2i =   ; б) со- ai отношения для коэффициентов обменных уп- равлений

2 α _i

P ²ⁱ     b ² , P ²¹

212^1. + 2e2j2L + P2L + P2L = 0 2     222

2αj bi       αbij      bj b2,12i,21-1   a 2; с) b2 = sa2, где j               ji ii i, j=1,2,...,n при i ^ j; 3) в неидеальном источнике устанавливается автоколебательный режим с амплитудой, равной величине полуоси эллипсоида an.

Тогда условия 1)–3) являются необходимыми и достаточными для стабилизации n – 1

n z i = 1

Г >ж a2

V ai

+1 bi   7

^ 1,

t ^i^

Будем искать такое управление с обратной связью, чтобы полная производная функции на движениях системы являлась полиномом четвертой степени по переменным состояния. Поэтому представляется целесообразным искать компоненты, стабилизирующие управление, в виде кубических полиномов: U i ( Y i , Y j , 1Y„ Y j ) = Р ₂ , ._2м УУ- + в 2 , ;2 , У 3 ' L e 2ij УУ ' L P yy

J== 7 =1 ^,

T                      i *j              T где     Y = ( У1, y 2,..„ y„),     Y = ( yv У2„.„ У n),

^Y = ( y i ,^у 2 , ™ ,y n ) — вектор состояния, скоростей и ускорений системы соответственно, вектор-функция U = (u , ,u ₂ ,...,u _n - 1 ) T - искомое стабилизирующее управление с обратной связью. Подсистема с номером n является искомым источником питания. Матрицы M , A – диагональные; A – матрица коэффициентов положительной обратной связи, определяющая неустойчивость процессов при отсутствии управления, где s i ² = ц ², при i = 1,2,..., n - 1, S' = w 2 .

апериодических звеньев в их пространствах состояний.

Таким образом, с учетом апериодичности группы процессов а² >  4ц², при i = 1,2,..., n – 1 следующие условия являются достаточными для стабилизации n – 1 апериодических звеньев в их пространствах состояний: систе-

ма состоит из неидеального источника питания и n –1 двойных апериодических звеньев; коэффициенты U управления с обратной свя-

зью по вектору состояния системы удовлетворяют соотношениям: коэффициенты внутри-

контурного управления: ^в 2 i ,2 i - 1 = ^а 2г , в 2 i ,2 i = ^ ; соотношения для коэффициентов об ⁱ менных уп ⁱ -

равлений

^в 2 i ,2 j

—

i

^a i^bi ^{+ а} i^b1 _R __R b i ²+ b ²   , ^{P 2i2j    P 2j2}i ,

^e 2i2j - 1 = _a 2 , где i = 1,2,... , n, S j = ^ j²_р b² = Э ²a² , j =

1,2,... , n при i ^ j . При выполнении этих условий

0 —a n J

Решение задачи опирается на следую-

щую теорему.

в неидеальном источнике устанавливается автоколебательный режим с амплитудой, равной величине полуоси эллипсоида a_n .

В частности, если в неидеальном источнике устанавливается автоколебательный режим с амплитудой меньшей величины полуоси a_n эллипсоида, тогда, по крайней мере в пространстве состояний одного из апериодических звеньев, возникают режимы вибраций в окрестности статического режима, звено теряет апериодичность и выходит на автоколебательный режим [1].

Отсюда вытекают два принципа виброизоляции процессов стабилизации апериодических звеньев, в случае, когда амплитуда установившегося процесса в источнике питания меньше a_n .

• 1.    Для того чтобы обеспечить виброизоляцию процессов стабилизации, достаточно ввести дополнительное апериодическое звено, движения которого поглощают вибрации, вызванные работой неидеального источника питания.

• 2.    Для обеспечения виброизоляции процессов стабилизации достаточно, чтобы неидеальный источник питания являлся двухконтурным. Причем оба контура должны быть колебательными.

• 2.    Алгоритм нелинейного поглощения вибраций

В случае устройства, работающего на двух колебательных звеньях, в пространстве исполнительного органа происходит демпфирование колебаний. Если динамика исполнительного органа описывается апериодическим звеном второго порядка, то установление автоколебательного режима в пространстве состояний управляющего колебательного контура определяет стабилизацию исполнительного органа в статическом режиме. Не теряя общности рассуждений, полагаем, что статический режим в пространстве исполнительного органа совмещен с началом координат. Заметим, что решение нелинейной задачи ста- билизации апериодического звена второго порядка посредством автогенератора эквивалентно задаче стабилизации двух апериодических звеньев первого порядка при выходе управляющего контура на режим генерации устойчивого автоколебательного процесса. Таким образом, приходим к следующей постановке задачи:

- a yi + ®2 y + u, (y„ yi) + u12 (y„ y2, yi, y2 ) = 0, - a2 y2 + ^ y 2 + u2 ( y 2, y2 ) + u21 ( y„ У2, y„ y2 ) = 0, y2 y

X i=1

y i ⁽ t ) + y ⁽ t )  ^ 1, lim y₂(t ) = 0, ^ = ® o .

• ²       2 t >+^    t ^+2          1    0

a i          i )

Согласно полученным достаточным условиям стабилизации, для амплитуды источника следует положить a 2 = Z 2 тогда, полагая в ₂ 4 = в ₄₂, получаем следующий расчет параметров синтеза.

• 1.    Коэффициенты в уравнении движения исполнительного звена - в ₄₁ = а ₄₄ Z _t ^{- 2} , - 2          ^а 44

• 2.    Коэффициенты для формирования контура обратной связи для обмена сигналами между неидеальным источником и исполнительным ^а 22 ^{+ а} 44     д д

^в 43 = ^а 44 a 2 , ^в 44 =    2 2 .

,       ω ²2 a 2²

органом - ^в 24 = _ю 2 Z 2 + _fl 2 _a 2 , ^в 42 = ^в 24 .

Численное моделирование представлено на рис. 1 (движение апериодического звена), рис. 1, 2 (выход источника питания на автоколебательный режим). В случае если амплитуда автоколебательного процесса источника питания не выходит на величину, равную полуоси эллипса, исполнительное звено начинает вибрировать (рис. 3, 4).

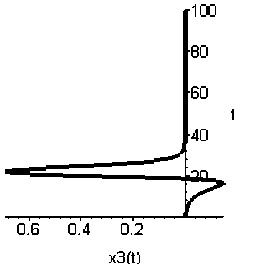
Рис. 1

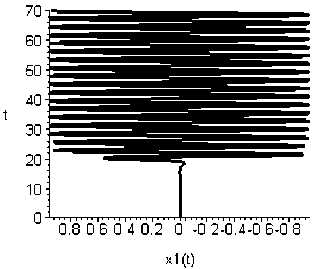
Рис. 2

62 А.С. Горобцов, Е.Н. Рыжов. О математических принципах построения областей виброизоляции

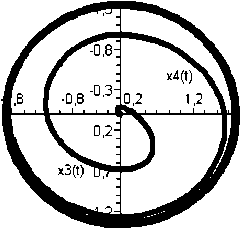
Рис. 3

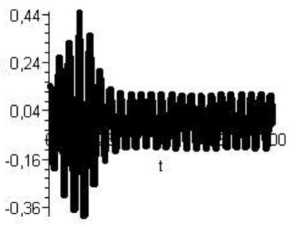
Рис. 4