О математической постановке задачи движения вязких сжимаемых теплопроводящих жидкостей в термоупругой трубке

При изучении динамических процессов в трубках, наполненных жидкостью, часто возникает необходимость учета как теплопроводности вязкой жидкости, заполняющей трубку, так и эффекта связанной термоупругости самой трубки, выполненной из некоего упругого материала. Отметим, что решение системы уравнений Навье—Стокса с учетом теплопереноса также сводится к решению связанной задачи для системы уравнений, включающих, например, вектор скорости течения жидкости и ее температуру. Поскольку задача термоупругости обычно ставится и решается в линейном приближении, то и систему Навье— Стокса целесообразно линеаризовать.

Ранее одним из авторов публиковались работы по сходной тематике, однако без учета теплопроводности и вязкости [1, 2]. Между тем, игнорирование этих факторов в ряде случаев может быть недопустимым.

В настоящей работе рассматривается в общем виде задача о движении вязкой сжимаемой теплопроводной жидкости в упругой теплопроводной трубке бесконечной длины, сводящаяся к решению линеаризованной системы уравнений Навье— Стокса и связанной системы термоупругости, описывающей динамику трубки. Подразумевается, что возмущение является гармоническим во времени.

СИСТЕМА УРАВНЕНИЙ НАВЬЕ—СТОКСА

Система уравнений Навье—Стокса для описываемого случая имеет наиболее полный вид [3]:

– уравнение неразрывности сжимаемой жидкости др +div (р v ) = 0,

– уравнение Навье—Стокса сжимаемой вязкой жидкости

Г dv             1                    Г п 1

р — + (vV)v = -Vp + nAv + ^ + — VV• v , (2)

Idt       'I

– уравнение теплопереноса сжимаемой вязкой жидкости

— + v •Vs ) = о' ^ + V •(kV T).(3)

. dt          J      8xk

Г dv d vk 2 dv1 d vz

Здесь °= n— + — - T^,k— 1 + ^5ik— — ^ оxk оxi 3 оxl J оxl вязкий тензор напряжений; ρ — плотность; p — давление; v — вектор скорости; T — абсолютная температура; η, ς — соответственно коэффициенты сдвиговой и объемной вязкости; κ — коэффициент теплопроводности жидкости; s — энтропия единицы массы жидкости.

Ранее подход к подобному решению для случая вязкой, теплопроводящей однородной безграничной жидкости был предложен, например, в работах [4–6]. Здесь придерживаемся подхода, изложенного в [6].

Уравнения (1)–(3) содержат пять уравнений при семи неизвестных. Для разрешимости этой системы необходимо добавить два термодинамических уравнения состояния, а именно зависимости плотности ρ и энтропии s через давление p и температуру:

р = р( p, T), s = s (p, T).(5)

В Приложении приведен подробный вывод следующих соотношений, лаконично изложенных, например, в [4, 5]:

dp = Y2dp - apdT,(6)

c ds = С dT - - dp.

Tρ

Расшифровка всех обозначений дана в Приложении.

Пусть в состоянии равновесия (покоя) жидкость характеризуется параметрами (используем индекс 0) v ₀ , p ₀ , ρ ₀ , T ₀ . Возмущенное состояние будем характеризовать штрихованными добавками с порядком приближения, равным количеству штрихов, а именно:      v — v ₀ + v ' + v '' + ...,

P = P о + P ' + P "+ ..., P = P o + P '+ P "+ ..., T = T o + + T ' + ... Аналогично и для параметров Y = Y 0 + Y ' + ..., a — a ₀ + a '+ ..., n = П 0 + П + -., S — s 0 + s ' + ... и т. д.

Рассмотрим вначале случай неподвижной изначально жидкости v ₀ — 0. Температура окружающей капилляр среды имеет постоянную температуру, также равную T ₀ .

Линеаризуем систему уравнений Навье— Стокса (1)–(3), оставляя стандартно только величины первого порядка малости (в переменных коэффициентах пока принимаются их значения, соответствующие равновесному состоянию температуры T ₀ и обозначаются нулем в нижнем индексе) и исключая переменные ρ ' и s ' с использованием соотношений (6), (7). Из этих соотношений имеем: др _ y 0 д p '         д T '       д s ' _ Ср о д T ' a 0 д p '

---— —;--- + a ₀ р ₀ ---,    — —-----, д t   c ₀ ² д t          д t         д t    T ₀ д t   р ₀ д t

Vs' — —p0 VT'- «0 Vp'. Окончательно линеаризо-T0

ванная система уравнений Навье—Стокса приобретает вид [ 5, 6 ]

—     Гa — -V -v'),(1а)

д t     Y 0 I 0 д t J’

P o —-V p + n 0 A v ' + 1 ^ 0 + ⁿ |VV- v ', (2а)

д tV

AT._ ± 0Г — - «T   .(3 а)

X 0 д t к д t

Здесь x ₀ — —0- — равновесный коэффициент ρ 0 c p 0

температуропроводности.

Для гармонических процессов с фактором e - ^{i — t} после исключения p ' с помощью выражения (1а) последние выражения приводятся к системе из двух уравнений [ 5, 6 ] (далее фактор e - ^{— t} опущен и выписаны выражения для амплитуд соответствующих величин при сохранении обозначений):

A v ' +	22 1 + ^L + _ i c o_ |vv. v' + i— v ' — « ° С ^V T ', (8)
	V 3   П 0    Y 0 —v 0 J          v 0       Y 0 v 0

A T '+ -^- T' — ^{Y 0} 1 V- v '.                  (9)

γ ₀ χ ₀      α ₀ χ ₀ γ ₀

Здесь v0 — n0 / р0 — кинематическая вязкость. После представления скорости v' через скалярный и векторный потенциалы v' — V^'+Vx ^'

в [ 5, 6 ] получено:

(A + в1 )Ф’ — - i^O4 T',(10)

β ₃

(A + в2)T' — (1 - Y0) в1 P.(11)

α ₀ χ ₀ γ ₀

Здесь e, — Y0®2/ (c02вз);(12)

в2 — i®(Y0 + e3 - 1) / (X0e3Y0);

e3 — 1 -i®Y0 (S0 + 4n0/3)/ (P0c02);

(A + k32) V' — 0,   k3 — 1+i.(15)

δv

Здесь S v — ^2v ₀/ to — глубина проникновения вязкой волны.

Таким образом, при решении линеаризованной системы уравнений Навье—Стокса получается система двух связанных уравнений в частных производных, например для переменных T ' и v ' (8, 9) или (10, 11) для переменных T ' и скалярного потенциала ϕ ' с коэффициентами, определенными из (12)–(14). Векторный потенциал ψ ' находится из простого уравнения (15).

СИСТЕМА УРАВНЕНИЙ ТЕРМОУПРУГОСТИ

В случае влияния температуры на деформацию, в частности, однородных изотропных упругих тел процесс описывается линеаризованной системой связанных динамических уравнений термоупругости [7, 8]:

P i ^ u = M i A u + ( X i + Ц 1 ) VV • u — rV T '+ P i f , (16) d t

АФ + ( к ' ) 2 Ф =-------- T ', ¹

2         ω ²

^{( i} ) = ( X + 2 M i ) / P i ,

A T ' + ^—T' = — i— HV- u .

Л

a T—± T

Л d t

—

ϖ

—

.

κ ₁

Здесь введены обозначения: λ1 , µ1 — упругие модули Ламе для тела; ρ1 — его плотность; f — массовая сила; Г = (3X + 2M^a, — термомеханическая постоянная; αt — коэффициент линейного κ термического расширения тела; Л = — — коэф-cε фициент температуропроводности; κ1 — коэффициент теплопроводности тела; cε — удельная теп-

Г T лоемкость п ри постоянной деформации; © = —0 ;

κ ₁

T ₀ — равновесная температура тела; ϖ — мощность внутренних источников тепла, отнесенная к единице объема.

При условии отсутствия массовых сил и тепловых источников уравнения термоупругости упрощаются:

P i '? ' = M i A u + (X i + M i) VV^ u — ГV T ', о t

После замены в (23) V • u = АФ и представления АФ из (22)

АФ =

Г

X + 2 M _i

T ' — ( к ' i ) ² Ф ,

получаем из (23)

A T ' + i ^— T' = — i— ©V • u = — i— ©АФ = Л

= i— © ( к ', ) 2 Ф

—

—^Г T ' I , X + 2 M _i J

откуда окончательно имеем

A T ' + i— —+ © T' = i— © ( к \ ) Ф . (Л J

Таким образом, для термоупругого тела получена связанная система уравнений (22), (24). Для векторного потенциала Ψ из (20) легко получить

( a + к '₃² ) T = 0,

k

k '₃²

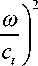
1 T + ©v-— -A г. Л 5 1        d t

2µ где ct = — — квадрат скорости поперечных ко-ρ1

лебаний в упругом теле.

Для стационарного процесса с временным фактором e ^— i ^{— t} система уравнений (i8), (i9) преобразуется соответственно к виду (обозначения для амплитуд оставляем прежними для упрощения записи)

^A u + ( X + M _i) VV • u + p— 2 u = rV T ',

A T '+ —T' = — i— ©V^ u . Л

После стандартного представления u = VФ + Vx T через скалярный и векторный потенциалы выражения (20), (21) преобразуются к виду

КРАЕВЫЕ УСЛОВИЯ

К уравнениям для однозначного их разрешения обычно добавляются краевые и начальные условия. Поскольку будем изучать стационарные задачи, ограничимся только краевыми условиями. Будем разделять температурные и механические краевые условия.

Механические краевые условия

Механические краевые условия на границе упругого тела и жидкости при наличии вязкости в жидкости подразумевают выполнение двух условий:

– непрерывность вектора скорости на границе раздела [3];

– непрерывность компонентов тензоров напряжений на границе [10].

При контакте жидкости или упругого тела с вакуумом подразумевается равенство нулю компонентов тензора напряжений на границе.

На бесконечной границе принимается условие отсутствия деформаций [10].

Температурные краевые условия

– Краевые условия температурного сопряжения на границе раздела жидкости и трубки при r = a 1 , где a ₁ — внутренний радиус трубки:

T '⁽ r = a l ) = T 2 *( r = a l ) ,

κ ₁

д T '( r = a 1 ) _    д T ₂'( r = a 1 )

-----------= k₂----------- д r               d r

Это означает непрерывность температуры и теплового потока на границе

– При теплообмене нагретого тела с окружающей средой принимается закон Ньютона конвективного теплообмена. Согласно этому закону, количество теплоты q , отдаваемое в единицу времени единицей площади граничной поверхности с температурой T ( x , t ) в окружающую среду с температурой T_out , равно

q ( x , t ) = a [ T ( x , t ) - To_Ut ] .             (26)

Здесь α — коэффициент теплопередачи; x принадлежит граничной (в данном случае торцевой поверхности).

Согласно закону Фурье и закону сохранения энергии, выражение (26) равно vT, а т 1      9 T (x, t)

^a [ T ( X , t ) ^- T ou, ] = ^-K— --- .

о n

Здесь x — точка поверхности тела (жидкости); κ — коэффициент теплопроводности тела (жидкости); n — вектор внешней нормали к поверхности теплообмена.

ВЫВОДЫ

Таким образом, в работе представлена математическая модель, позволяющая рассчитывать стационарные температурные поля и поля упругих колебаний в термоупругой трубке и вязкой теплопроводящей сжимаемой жидкости при условии связанности упругих и тепловых процессов. Освещены термодинамические процессы и вопросы постановки краевых условий.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках Федеральной целевой программы "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007– 2013 годы" и опытно-конструкторской работы "Раз- работка генетического анализатора для секвенирования и фрагментного анализа ДНК" (шифр заявки "20112,2-522-014-001", Государственный контракт № 16,522,12,2014 от 10 октября 2011 г.).

Приложение.

ТЕРМОДИНАМИЧЕСКИЕ СООТНОШЕНИЯ

Здесь приведем некоторые термодинамические соотношения, следующие из первого начала термодинамики (закона сохранения энергии) [3, 11– 14]. Рассмотрим однофазную систему (однородная среда). Наиболее важными переменными состояния термодинамической системы являются абсолютная температура T , плотность ρ, удельный объем V (объем единицы массы V = —), энтропия единицы массы s , внутренняя энергия единицы массы ε и давление p . Структура однофазной системы определяется функциональными соотношениями между переменными состояния. Следуя Гиббсу, выбирают в качестве основного соотношения [11]

s = s ( s , V ) (П1)

(функция ε ( s , V ) предполагается заданной заранее) и принимаются следующие определения p и T :

dsd

Р = —, T = — д V

.

(П2)

Полное дифференцирование (1) приводит с учетом (П2) к важному выражению:

Tds = ds + pdV = ds --p^dp,(П3)

ρ ²

которое для обратимых процессов (в этом случае выполняется равенство T d s = 5Q , а элементарная работа при квазистатическом расширении системы под воздействием всестороннего давления равна 5A = p d V ) сводится к выражению, совпадающему с формулировкой первого начала термодинамики:

5Q = d s + p d V = d s - -p ^d p .       (П4)

ρ ²

Здесь δQ — элементарное количество теплоты, подводимое к удельному объему V .

Между параметрами равновесного состояния термодинамической системы существует аналитическая связь [12]. Различные соотношения между переменными состояния T , ε , s , V , p и ρ, которые можно получить из (П1)–(П4), называются уравнениями состояния. Ясно, что, зафиксировав две переменные (в данном случае s и V ), можно определить все остальные. Уравнение, связывающее независимые внутренние и внешние параметры в равновесном состоянии системы, называется уравнением состояния. В общем виде это уравнение можно записать так

удельных теплоемкостей при постоянном давлении и объеме. Тогда для первой производной из (П6а) имеем

(d P 1 ( ^a p J T

γ

— peT = YPes = — .

c

(П8)

F ( p , V , T ) — 0,               (П5)

если в качестве независимых параметров принимается давление, температура и объем.

Рассмотрим два термических уравнения состояния, которые в дальнейшем будут использоваться:

F ( p, p , T ) — 0, которое разрешим относительно p

Упростим вторую производную справа в (П6а). Используя изобарный коэффициент расширения [13, т. 5, с. 82]

¹ (д V ) _ ¹ (d p )

V (a t J p    p (a t J p

имеем

P = p ( P , T ) ,              (П6)

dp | dT Jp

— ap .

(П9)

и F 2 ( s , p , T ) — 0, которое разрешим относительно s

s — s ( p , T ) .                 (П7)

(a s I Далее упростим выражение I 1 из (П7а).

( ^{a т} J p

Перепишем (П6), (П7) в дифференциальной форме:

Имеем [13, т. 5, с. 77]

(asj cp— T (aTJ . Откуда полУ-

dp =

(p 1

(ap J T

d p +

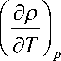
d T ,

(П6а)

чаем

a s j a T J p

c p T

.

(П10)

ds =

I— 1 (ap J T

d p +

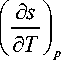
d T .

(П7а)

Наконец, найдем выражение

для

(a s)

— 1 из

(ap J T

Преобразуем выражения (П6а) и (П7а), используя известные термодинамические соотношения. Для первой производной справа в (П6а) понадобятся следующие соотношения. Для скорости звука в жидкостях справедливо выражение [13, т. 4, с. 546]

(П7а). Согласно [14, с. 277] имеем

as 1

(^a p J T

—

a v j — 1 (ap j aт Jp" p2 (aтJp

.

Откуда

c ^— в^Р ’

^L 1 ( ^a p J T

α

—

.

ρ

(П11)

где β_s — адиабатическая сжимаемость среды

e s —¹ U p 1 - P V^d p Js

Учитывая выражения (П8)–(П11), (П6а) и (П7а) преобразуются к виду

которая связана с изотермической сжимаемостью среды β_T

γ dp — — dp — ap d T, c2

(П6б)

вт — -ρ

^p 1 ( ^a p J T

d s — c p d T — — d p .

Tρ

(П7б)

соотношением в_т — в , где Y — ~ — отношение

cV

Отметим, что в работах [5, 6] последние выражения были приведены ранее в окончательном виде без вывода и расшифровки коэффициентов α , γ и c .