О механизме адиабатического сдвига при высокоскоростном нагружении материалов

A characteristic feature of instability of plastic deformation appears to be the localized shear, which very often takes place under high velocity loading. Mathematical modeling of shock is carried out in the research. The analysis is based on the statistic-thermodynamical theory of solid with microcracks,worked out earlier.The proposed description of plastic shear instability includes tonsorial structurial parameter, which specifies the volume concentration and preferred orientation of defects.

Для понимания физики и механики пластичности большой интерес представляет изучение локализации пластической деформации [1]. Ярким примером неустойчивости пластического сдвига следует считать формирование так называемых полос адиабатического сдвига при ударно-волновом нагружении материалов [2]. Полосы адиабатического сдвига возникают при взрывном нагружении, высокоскоростном соударении и играют значительную роль в ряде таких явлений, как дробление, эрозия, пробивание.

Локализация пластического сдвига является следствием резких структурных изменений в материалах и может сопровождаться полиморфными превращениями, фрагментацией, ориентационной и ротационной неустойчивостью.

Фрагментация структуры является естественной предпосылкой для зарождения и роста микротрещин. Микротрещины возникают в местах структурных несовершенств: участков с повышенной плотностью дислокаций, границ блоков и т.п. В настоящее время установлено, что зарождение и рост микротрещин играют существенную роль в процессе деформирования и разрушения материалов [3,4]. Особое значение в возникновении пластической неустойчивости имеют структурные изменения в материале, связанные с коллективными процессами в системе микротрещин.

Обсуждаемый класс явлений в последние годы исследуется нелинейной физикой деформирования и разрушения твердых тел [5-13], рассматривающей данные эффекты с позиций неравновесных кинетических переходов.

В настоящее время установлено, что деформирование и разрушение металлов сопровождается множественным зарождением и ростом микротрещин [14], кинетика которых существенно влияет на разрушение и релаксационные свойства [15].

В работах [5-7] предложена статистико-термодинамическая модель среды с микротрещинами. Система микротрещин описывается тензорным параметром плотности микротрещин p_ik . Тензор p_ik является независимой термодинамической координатой системы и характеризует объeмную концентрацию и преимущественную ориентацию микротрещин. Определяющие уравнения пластически релаксирующего тела с микротрещинами имеют вид:

ст = У - a p,

п = Y e^p — в Р ,

• (1)    p ′      (2) ^Δ p lm

σ ik ⁼ L iklm e lm    L iklm       ,

Δ t

• (2)   p ′      (3) ^Δ p lm

  .

  
  

пik = Liklmelm   Liklm ik iklm lm iklm  Δt

Здесь ξ, α, β, L(ν) - кинетические коэффициенты. В уравнениях (1)-(4): п = iklm                                                                                            ∂pik термодинамическая сила, действующая на систему, когда значения pik отличаются от равновесного; σi′k, eipk′, pik, пik и σ, ep, p, п - бесследовые и изотропные компоненты напряжений, пластических деформаций, параметра плотности трещин и тензора пik ; ΔPik = dpik -ωil pik -ωlk pil - тензорная производная по времени (производная по Яуманну Δtdt il ik lk il

[16]).

Уравнения состояния включают соотношения релаксационного типа для тензора напряжений (1),(3) и уравнения движения (2),(4) для параметра P_ik . В этих уравнениях учтены "перекрестные" эффекты: влияние трещинообразования на релаксационные процессы и пластичности на кинетику роста p_ik . В дальнейшем считаем, что пластические деформации подчиняются условию Sp e_i^p_k = 0 , а среднее напряжение определяется упругими составляющими тензора деформаций

ε _i ^e _k = 12 µ ( σ _ik - σδ _ik ) + 19 K σδ _ik

( µ , K- модули сдвигa и объeмного сжатия).

Коллективные эффекты в ансамбле взаимодействующих микротрещин сопровождаются структурными изменениями, вызывающими локализацию пластической деформации. Одним из видов локализованной пластичности является адиабатический сдвиг при высокоскоростном нагружении. Наиболее ярко неустойчивость пластического сдвига проявляется при высокоскоростном налетании ударника конечного размера на преграду. При определeнных условиях нагружения имеет место так называемое "выбивание пробки" [18]. При этом пластическая деформация (или разрушение) локализуются в узкой области, располагающейся по периметру цилиндрического ударника.

Рассмотрим задачу о динамическом нагружении круглой пластины при налетании цилиндрического ударника меньшего диаметра, имеющего общую с ударяемой пластиной ось симметрии.

При распространении волны сжатия эволюция системы микротрещин сопровождается слабым объeмным взаимодействием дефектов, объемная составляющая p= 3 Sp pik мала и практически не влияет на развитие разрушения. Основной вклад в процесс разрушения вносят ориентационно-сдвиговые компоненты pik, интенсивность которых характеризуется переменной p′ = (p′ik p′ik)1/2. Вводя для описания ансамбля дефектов переменные р и p', решаем систему определяющих уравнений (1)-(5) совместно с уравнениями движения. Функции пik и П, представлены в работе [7] через статистические интегралы.

Входящие в уравнения коэффициенты определялись из опытов по деформированию алюминия при ползучести [4].

В различных вариантах расчeтов ударник рассматривался упругим и абсолютно жeстким. Движение ударника в деформируемой среде описывается уравнением динамики твeрдого тела. При численной реализации использовалась явная разностная схема второго порядка точности [17].

Необходимым условием выбивания "пробки" является относительно высокая скорость ударника, его достаточно большие вес, плотность и длина. Локализация пластической деформации в форме образования характерной поверхности сдвига может произойти только тогда, когда кинетическая энергия ударника, превышающая некоторую предельную величину, передается мишени за достаточно малые времена, соизмеримые со временем распространения ударной волны по толщине пластины. При этом переданная энергия не распределяется по всему объeму мишени, а практически целиком затрачивается на образование поверхности пластического сдвига.

Если при соударении количество переданной энергии ниже порогового уровня, поверхность пластического сдвига, имеющая вид "светлой гладкой области" [18], распространяется только на часть толщины пластины. Вторая область ("тeмная с крупными зeрнами") свидетельствует о разрушении в виде грубого излома. При увеличении скорости соударения величина сдвиговой зоны увеличивается до тех пор, пока не охватит всю толщину образца. При последующем увеличении скорости соударения характер разрушения не меняется. Пластическое течение неразрывно связано с процессом трещинообразования [3,4]. Последний влияет на пластические микросдвиги и пластические ротации, которые можно связать с изменением ориентационной составляющей тензора плотности микротрещин, характеризуемой p ′ _ik .

При достижении некоторых критических параметров нагружения происходит быстрое увеличение концентрации микротрещин; в системе микротрещин реализуется неравновесный (кинетический) переход, который сопровождается скачкообразным изменением бесследовой компоненты p ′ _ik . На рис.1 представлено изменение параметра плотности трещин p ‘ по толщине и радиусу пластины при t=0.7 мкс. Кинетический переход приводит к резкому увеличению темпа релаксации напряжений, скачкообразному росту пластических деформаций, существенно изменяет структуру волнового фронта. Волновой профиль расщепляется на упругий предвестник и следующую за ним пластическую релаксационную волну. На рис.2 показано изменение σ _z по толщине и радиусу пластины в момент времени t=0.7 мкс. Наиболее интенсивно процесс трещинообразования и релаксации идет в узких полосах по периметру ударника. Как следствие, скорости пластических деформаций в рассматриваемых зонах больше, чем в центре. Большая величина пластических деформаций вызвана характером распределения напряжений по контуру ударника и большим темпом кинетического перехода в системе микротрещин. Hа рис. 3 показано распределение интенсивности скоростей пластических деформаций при t=0.7 мкс. По краям ударника формируются локальные области, в которых способность материала к пластической деформации резко возрастает.

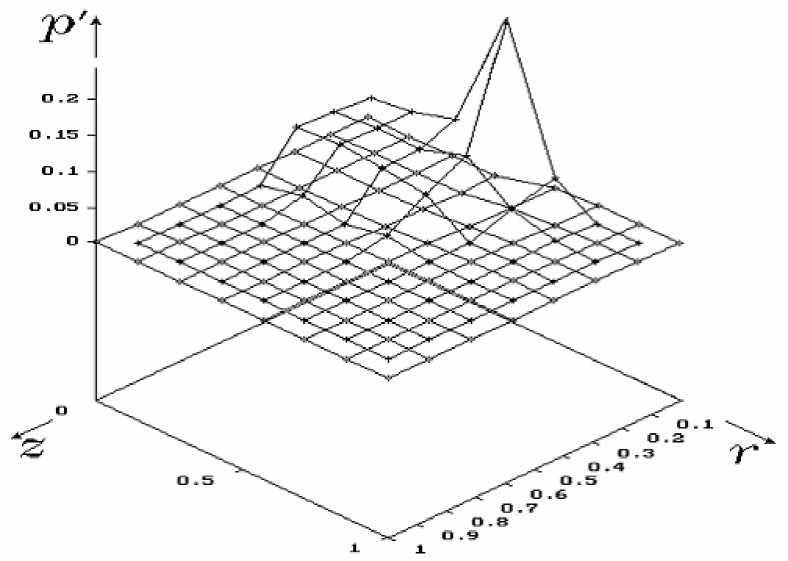
Рис.1. Изменение параметра плотности трещин p‘ по толщине и радиусу пластины при t=0.7 мкс

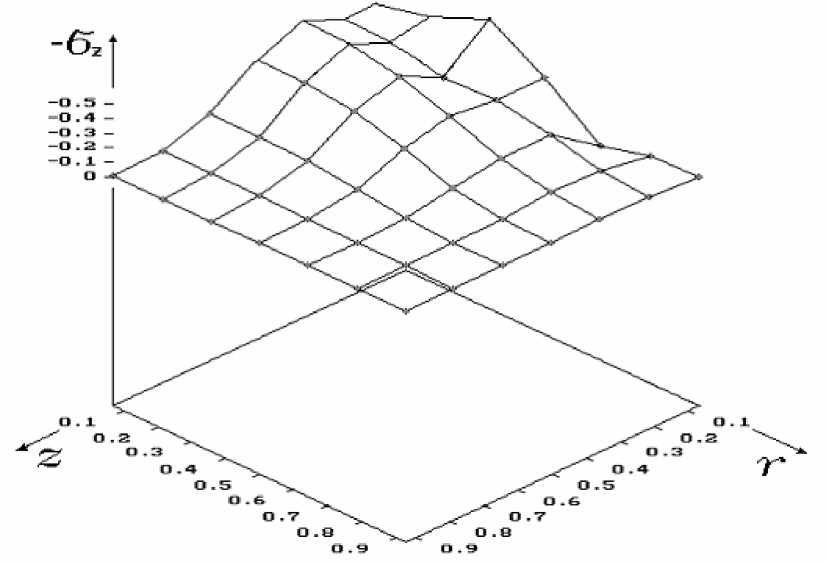
Рис.2. Изменение σ _z по толщине и радиусу пластины в момент времени t=0.7 мкс

Локализованный и пороговый характер процесса выбивания "пробки" подтверждается экспериментальными результатами [18-20].

В областях неустойчивости пластического сдвига качественно ситуация аналогична фазовому переходу первого рода. Ориентационный переход сопровождается появлением более упорядоченной системы микротрещин и формированием направлений "легкого" скольжения. Для того чтобы область пластического сдвига проходила по всей толщине преграды, необходима реализация ориентационно-кинетического перехода последовательно в каждом сечении.

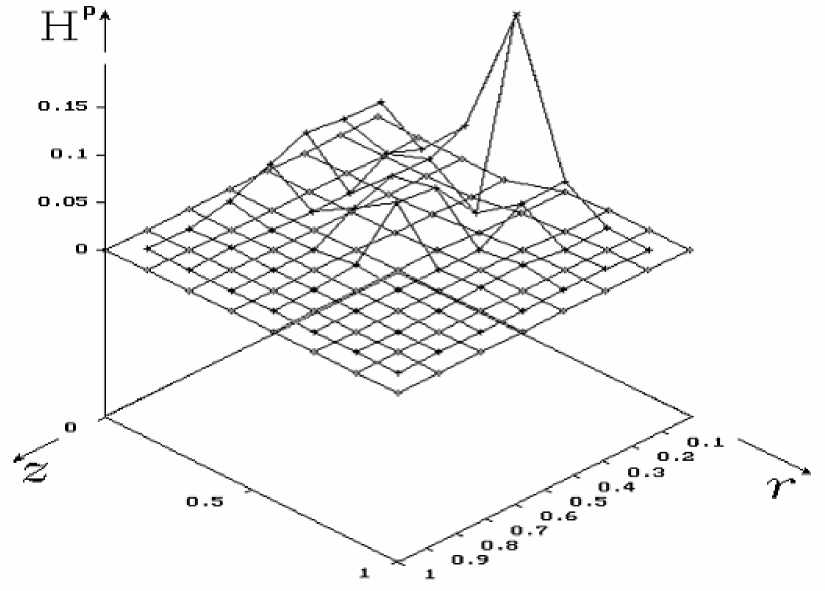
Рис.3. Распределение интенсивности скоростей пластических деформаций при t=0.7 мкс