О механизме осевого подъема жидкости в результате свободного падения цилиндрического сосуда

По меньшей мере с начала шестидесятых годов М.А. Лаврентьев [1] был озабочен объяснением эффекта удивительно высокого всплеска воды, который формируется в момент соударения заполненной про- бирки с массивной горизонтальной плитой (столешницей). Высота подъема «выбитой» из пробирки воды на порядок превышала высоту падения пробирки. Установлено, что эффект не зависит от конфигурации донышка пробирки и усиливается при увеличении жесткости материала плиты. Там же (в главе «Неустановившиеся течения») в рамках неупругих моделей жидкости и твердого тела приведена качественная интерпретация эффекта. Количественные оценки не получены, потому что не учтены три весьма существенных обстоятельства. Во-первых, не учтен фактор превращения тяжелой жидкости в невесомую, в момент ликвидации удерживающей пробирку вертикальной связи, что влияет на конфигурацию свободной поверхности (мениска). Подобно системе отсчета «падающего лифта» [2] связанная с пробиркой система координат становится инерциальной. Это должно отражаться на величине капиллярной постоянной [3] воды, которая в поле тяжести равна 4 мм. Во-вторых, невозможно объяснить многократные отскоки пробирки от плиты, игнорируя упругие свойства стекла. В-третьих, возможность использования при анализе процесса модели несжимаемой жидкости определяется соответствием его характерных параметров неравенству s/c << τ [3], в котором c – скорость звука в жидкости (для воды c ≈ 1500 м/с), а s и τ – характерные значения расстояния и промежутка времени, соответствующие существенному изменению скорости жидкости. Значения τ могут быть получены из соотношений контактной задачи [4]. Оценочные значения: s/c ≈2H/c ≈ 200 мкс (высота пробирки H = 150 мм); для стальной плиты τ1 ≈ 140 мкс, а для древесноволокнистой плиты (ДВП) τ2 ≈ 350 мкс. Легко увидеть, что они не соответствуют неравенству. Можно заключить, что при анализе описанного процесса модель несжимаемой жидкости является слишком грубым приближением.

1.    Постановка задачи и динамика пустой «мензурки»

Пробирку можно рассматривать как маломасштабную физическую модель цилиндрического сосуда. Поскольку конфигурация донышка значения не имеет, в качестве расчетной модели можно рассматривать «мензурку», которая состоит из цилиндрической стеклянной трубки с размерами пробирки и скрепленного с ней на нижнем торце плоского жесткого донышка пренебрежимо малой толщины. В лабораторной системе координат скорость падения мензурки с высоты l0 = 10 см на плиту равна u0 ≈ 1,4 м/с. Плиту следует считать абсо- лютно жесткой плоскостью. При их соударении обеспечивается плоский контакт.

Параметры «мензурки». Модуль упругости стекла E ~ 640¹⁰ Па; коэффициент Пуассона р ~ 0,25; плотность р 1 ~ 2500 кг/м³; скорость звука c 1 ~ 5000 м/с; внутренний радиус а ~ 6,5 мм; наружный - b ~ 7,5 мм; высота H ~ 150 мм, масса m ~ 16 г. Высота водяного столба h <  H . Модуль объемного сжатия воды G ~ 2,2^10 9 Па; ее плотность р₂ ~ 1000 кг/м³; скорость звука c ₂ ~ 1500 м/с. Высота подъема жидкости L , высота падения пробирки l. Не будем учитывать, что по формуле Н. Е. Жуковского скорость осевого возмущения c * = c ₂(1 + 2 а-G/ (( b - а ) E ))^-1/2 ~ ~ 1250 м/с.

Волновой анализ следует проводить в системе координат ( r , z ), неподвижной относительно среды. В исходном состоянии твердая и жидкая среды неподвижны в инерциальной системе отсчета, где с ускорением g вверх поднимается плита, ударяя (в начальный момент времени t = 0) со скоростью и 0 по донышку мензурки, заполненной жидкостью. В результате в начальный момент донышко генерирует распространение двух плоских волн: давления в водяном столбе и напряжения в стенке мензурки; можно полагать, что они имеют ступенчатый профиль. Распространение волны в стенке по отношению к воде является сверхзвуковым, поскольку c । c ₂ ~ 3,3. Параметры гидравлической волны соответствуют соотношению

Р ( t , z ) = p 0 S ( c 2 t - z ), (1)

где p 0 = p₂ и 0 c ₂ ~ 2,1 МПа; и ₀ - осевая скорость воды в инерциальной системе координат; S ( x ) - ступенчатая функция [5] ( S ( x <  0) = 0; S ( x >  0) = 1; S (0) = 1/2).

При t = 0 в стенке мензурки генерируется волна осевого сжатия о . за фронтом которой массовая скорость выравнивается со скоростью плиты и 0 . При отражении она превращается в волну растяжения о + .

о . = - о₀ U ( c 1 1 - z ) (0 <  t <  t 1 ); о₊ = о₀ U ( c 1 t + z - 2 H) ( t 1 <  t < 2 1 1 ), (2) где 1 1 = H/c 1 ~ 30 мкс; неотрицательная величина о₀ = р 1 и 0 c 1 ~ 18 МПа. При t = 2 t 1 мензурка отделяется от плиты со скоростью, близкой к 2 и 0 .

Квазистатическое нагружение мензурки до напряжения о0 приводит к ее «пуассоновой» деформации, которая не зависит от z (одинакова по высоте мензурки); модуль деформации 5 = ро0a/E ~ 0,5 мкм. Пе- реход к динамическому нагружению ступенчатыми волнами (2), делает «пуассоновы» деформации функциями волновых аргументов; при этом изменение радиуса a до a + δ происходит непосредственно за фронтами волн.

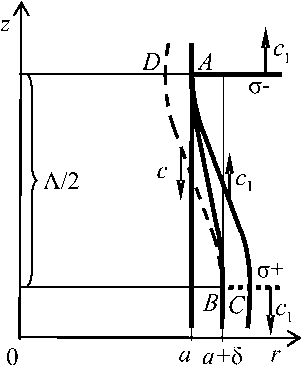
Рис. 1. Радиальные деформации стенки за фронтами напряжений σ – и σ +

Кольцевые элементы, на которые можно условно разделить упругую стенку мензурки, можно рассматривать, как линейные осцилляторы. Основная форма их радиальных колебаний – цилиндрически симметричные колебания. Их собственная частота ω = c 1 / a ≈ 8∙10⁵ с^–1 [6], период колебаний T ≈ 8 мкс. В результате радиальная деформация бежит вдоль оси как волна длиной Λ = c 1 T ≈ 40 мм.

В бегущем скачке сжатия σ – происходит мгновенное увеличение радиальной координаты положения равновесия осцилляторов на величину δ. В волне растяжения σ + она уменьшается на ту же величину, и также скачком. Каждый из осцилляторов ведет себя как «отпущенный» маятник. В связи с этим после прохождения σ – и σ + радиальное перемещение равно 2δ. Оно соответствует половине косинусоиды, показанной на рис. 1 кривой AC . То есть амплитуда радиальной скорости стенки пустой мензурки ωδ ≈ 0,4 м/с. Это значение характерно также для кривой BD , соответствующей движению стенки за волной σ + в незаполненной жидкостью части мензурки.

2.    Радиальное взаимодействие мензурки и водяного столба

Даже при h = H амплитуда колебаний стенки не может быть меньше величины 5/2, заданной кинематикой процесса; движение соответствует кривой AB. Волны напряжения (2) порождают деформации Д a и Д a + , которые определяются соотношениями

Д a_- = 0,55(1 - cosm( t - z/c 1 )), (0 < m( t - z/c 1 ) < n);

Aa + = -0,55(1 - cosw( t + z/c 1 - 2 H/c 1 )), (0 < w( t + z/c 1 - 2 H/c 1 ) < n).

Легко увидеть, что при z = H , Д a_- + Д a + = 0. Нетрудно убедиться, что эта сумма при изменении уровня воды h в интервале значений от H- Л/ 4 до H пропорциональна sin(( H - z )/Л). (Уменьшение L до нуля при стремлении h к H наблюдается в опытах.)

Деформации стенки мензурки приводят к генерированию радиальных акустических волн в водяном столбе. На порядок больший акустический импеданс стекла по сравнению с тем же параметром воды позволяет при оценках считать, что на перемещение стеклянной стенки вода реагирует, как на движение абсолютно жесткого тела.

Наклон деформаций AB , BC и CD (см. рис. 1) к оси z ничтожно мал, меньше 10^-4. В связи с этим даже деформированную внутреннюю поверхность мензурки можно считать цилиндрической. В силу неразрывности жидкости при r = а генерируется сходящаяся цилиндрическая волна; ее длина X = c₂/ю ~ 12 мм. Амплитуда радиальной скорости стенки совпадает с амплитудой волновой скорости, поэтому w a = ю5 ~ ~ 0,4 м/с. При r = a в гармонической полуволне сжатия, за фронтом волны растяжения о₊, амплитуда давления p_a = р₂ w_ac ₂ ~ 0,6 МПа.

Известно [3], что при X <<  r амплитуды p и w нарастают пропорционально 1/ r ^1/2; при сопоставимых с длиной волны значениях радиуса в выражении волновой скорости необходимо учитывать движение жидкости как несжимаемой среды. Из приведенного в [7] анализа следует, что при r < X/2 движение определяется в основном неволновой скоростью. В связи с этим при оценке в выражении скорости волновым членом можно пренебречь. В таком случае амплитуды давления и скорости в сходящейся цилиндрической волне приближенно определяются соотношениями

P ( r) = P a ( a/r )^1/2; W ( r ) ~ W a (( a/r ). (3)

Волны (1) и (3) независимо распространяются в водяном столбе, свободная поверхность которого весьма существенно изменяется.

На рис. 2 пунктирной кривой 1 показано осевое сечение исходного мениска, он соответствует мензурке, покоящейся в поле тяжести, его осевой габарит δ 1 . Прерывистая дуга 2 с центром в точке O соответствует сферическому мениску, который устанавливается при свободном падении мензурки. Краевой угол смачивания стекла водой θ ≈ 35°, радиус сферы R = a/ cosθ ≈ 8 мм, осевой габарит мениска δ 2 = = R (1 – sinθ) ≈ 3,4 мм. В процессе его установления на свободной поверхности генерируются капиллярные волны со слабым затуханием, что приводит к увеличению длительности процесса установления. В результате время установления мениска может превышать время падения мензурки. Другими словами, внезапное изменение гравитационного поля от g до нуля в системе отсчета мензурки приводит к тому, что в момент ее соударения реализуется неустановившаяся конфигурация мениска. По-видимому, его осевой габарит δ 3 > δ 2 . В связи с действием инерции его геометрия может быть близка, например, к поверхности скругленного конуса, осевое сечение которого дано кривой 3 . Радиус скругляющей сферы R * ≈ 1,5 мм; O * – центр сферы; β ≈ 45° – половинный угол конуса, r * = R * cosβ ≈ 1,1 мм – радиус сопряжения сферы и конической поверхности.

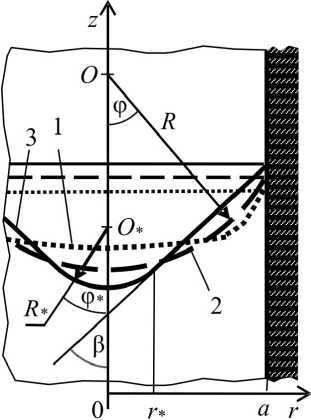
Рис. 2. Мениски водяного столба: 1 – исходный; 2 – установившийся сферический;

3 – неустановившийся (пример)

Картина отражения волн (1) и (3) от сферического мениска с радиусом R (если бы он установился) в рамках локально-плоского подхода [3, 7] схематически представлена на рис. 3; здесь ф - текущий угол (д1пф = r/R ). Отражение плоской волны приводит к распределению скоростей жидких частиц свободной поверхности: u ( r ); отражение цилиндрической волны - к распределению w ( r ). Суммарная скорость составляла бы v = u + w . Модули скоростей определяются соотношениями и(r ) = 2 и ₀(1 - ( r/R )²)^1/2 и w(r ) - 2 w a ( a/R ). Поскольку все скорости направлены в центр сферы O , модуль суммы векторов равен сумме их модулей. Модуль v’ определяется функцией

1/2

v ( r ) - 2 ( и ₀(1 - ( r / R )² ) + w_a ( a / R ) ) . (4)

Из (4) следует, что при плоском мениске ( R = го ) v ( r ) = 2 и о . То есть в точках свободной поверхности, представляющей собой круг радиусом a , скорости одинаковы и направлены вертикально. При сферическом мениске жидкие частицы симметрично сходятся в центре O , что должно приводить к их вертикальному движению, при котором модули скоростей сохраняются. Как результат, должен формироваться осевой подъем, в котором скорости соответствуют функции (4), показанной серой линией на рис. 4. При сферическом мениске максимальное значение v' равнялось бы 3,5 м/с, поскольку в лабораторной системе координат модуль скорости частиц в струе v = v - и о , максимум скорости v составляет 2,1 м/с. Наблюдатель фиксировал бы слабый эффект, поскольку высота подъема в поле тяжести составляла бы L ~ 0,22 м ~ 2 l ₀.

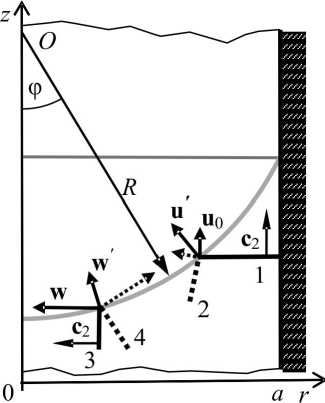
Рис. 3. Отражение волн от сферического мениска: 1 - плоская волна сжатия, 2 - волна разрежения, 3 - цилиндрическая волна сжатия, 4 - волна разрежения; и¹ и w' - скорости жидких частиц

Оценка скоростей U ’ и W ’, соответствующих неустановившемуся мениску 3 (см. рис. 2), аналогична оценке u и w . Направления скоростей совпадают, они нормальны свободной поверхности. При r ≤ r * их модули оцениваются выражениями

U' ( r ) ≈ 2 u 0 (1 – ( r/R * )²)^1/2; W' ( r ) ≈ 2 w a ( a/R * ). (5)

При r ≥ r * они соответствуют выражениям

U' ( r ) ≈ 2 u 0 sinβ; W' ( r ) ≈ 2 w a ( a/r ))cosβ.

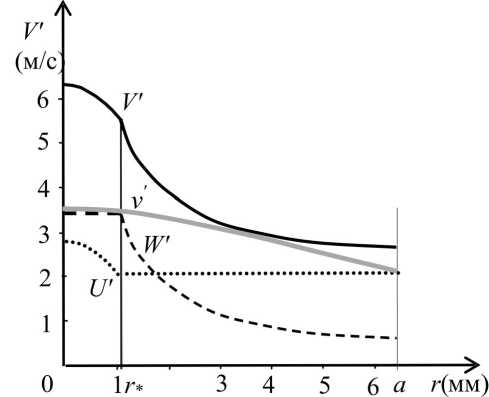
Рис. 4. Распределения скоростей: v^' ( r ) – сферический мениск, V' ( r ) –неустановившийся мениск (пример)

На рис. 4 распределение U' ( r ) показано пунктирной линией, а W' ( r ) – прерывистой. Их сумма V' ( r ) показана непрерывной черной линией. Величина V' ( r ) максимальна при r = 0, V' (0) ≈ 6,3 м/с, что в лабораторной системе координат соответствует значению V (0) ≈ 4,9 м/с. Следовательно, при неустановившемся мениске L >  1 м, то есть на порядок больше l 0 . При этом «вершина» всплеска образована наиболее быстрыми частицами, которые генерируются «донышком» сферической части мениска. Поверхностное натяжение приводит к компоновке жидких частиц в капли диаметром 2–3 мм, поднимающиеся более чем на метр от плоскости плиты.

3.    Результаты экспериментальной проверки

Значения L >> l 0 наблюдаются при замене воды на другие жидкости, если они хорошо смачивают стекло, в частности на этиловый спирт. Его способность к смачиванию выше, чем у воды, в то же время поверхностное натяжение – ниже.

Проводились дополнительные опыты, при которых поочередно блокировалось распространение либо плоских, либо цилиндрических волн. В первом случае над донышком устанавливался воздушный амортизатор, представляющий собой резиновый шарик высотой 20 мм. Его наличие приводило к обнулению значения U' в (5), в то же время динамика стенок пробирки и формирование мениска не изменялись. Падение пробирки с амортизатором с высоты l 0 = 10 см приводило к подъему водяных капель на высоту до 0,2 м, что хорошо согласуется с величиной максимальной скорости V ≈ W' – u 0 ≈ 2 м/с. Во втором случае пробирку заменяли стальной плунжерной парой. Плунжер частично вводился в цилиндр и фиксировался в нем усилием, компенсирующим вес. Открытая (сверху) полость цилиндра частично заполнялась водой или этиловым спиртом. Поэтому в момент соударения с плитой плунжер останавливался, а цилиндр продолжал падение, что свидетельствовало об отсутствии в нем каких-либо напряжений и деформаций. В связи с этим цилиндрическая волна не генерировалась, в результате значения W' в (5) обнулялись. В опытах с плунжерной парой высота подъема L равнялась l 0 , так как максимальное значение V = u 0 .

Влияние внезапного перехода от «тяжелой жидкости к невесомой» на геометрию мениска исследовалось методом теневой киносъемки начальной стадии падения одинаковых пробирок. Использовалась цейсовская установка TEPLER- 80 и видеокамера CEMER LINC , режим съемки – 500 кадров в секунду. Пробирки заполнялись приблизительно на треть высоты либо водой, либо этиловым спиртом. Симметричная подвеска на нити за открытый конец обеспечивала их вертикальную ориентацию; запуск осуществлялся путем пережигания нити. Результаты представлены на рис. 5, где для наглядности изображены поперечное (рис. 5, а ) и осевое (рис. 5, б ) сечения пробирки, которую «пронизывает» пучок параллельных световых лучей.

Преломление лучей приводит к их рассеянию и образованию теневых зон на изображении; непреломленные (прямые) лучи образуют светлые зоны. На сечении (см. рис. 5, а ) показано рассеяние лучей по горизонтали в случаях пустой (верхняя половина) и заполненной жидкостью (нижняя половина) полости пробирки. На сечении (см. рис. 5, б ) показано их рассеяние по вертикали при прохождении мениска. Понятно, что осевые размеры мениска и обусловленной им теневой зоны практически одинаковы. Сопоставление кадров видеосъемки (рис. 5, в )

свидетельствует о росте осевого размера водяного мениска в 1,8 раза. Аналогичная пара кадров (рис. 5, г ), на которых пробирка заполнена спиртом, подтверждает эффект: осевой габарит мениска вырастает в 3,5 раза. Кадры на рис. 5, в свидетельствуют об осевых габаритах менисков (см. рис. 2) 5 1 ~ 2,5 мм и 5₃ ~ 4,5 мм. Таким образом, экспериментально подтверждено предположение, выраженное неравенством 5₃> 5₂ ~ 3,4 мм. Характерная длительность нарастания 5 от 5 1 до 5₃ составляет п 1 ~ 0,05 с; ей соответствует высота падения l 1 = g n 2 /2 ~ 1,2 см. Кадры теневой съемки показывают, что реальный профиль неустано-вившегося мениска отличается от кривой 3 (см. рис. 2). Для получения значений L >> l ₀ важно наличие на свободной поверхности центрального скругления радиусом R * <  1,5 мм.

б                              в                                 г

Рис. 5. Рассеяние световых лучей при прохождении сквозь пустую и заполненную жидкостью пробирку: а - горизонтальное преломление; б - вертикальное преломление на мениске; в - исходный и неустановившийся мениски воды; г - исходный и неустановившийся мениски этилового спирта

В связи с этим легко объяснить отсутствие больших значений L в том случае, когда удар по неподвижно висящей над столом пробирке со скоростью и о наносится поднимающейся плитой (молотком). Дело в том, что в момент соударения мениск соответствует устойчивой кривой 1 , а не ее неустановившейся форме, типа кривой 3 (см. рис. 2). По той же причине не наблюдаются большие значения L , если пробирка равномерно опускается на плиту со скоростью u 0 .

В соответствии с соотношениями [3] для капиллярных волн малой амплитуды в отсутствие сил тяжести при изменении радиуса цилиндрического сосуда с коэффициентом подобия к время роста мениска nк изменяется пропорционально к3/2. Легко увидеть, что при этом характерная высота lk ≈ l1k3. Коэффициент k = 4 соответствует радиусу цилиндрической части обычной бутылки. Следовательно, для сохранения эффекта высота ее падения на покрытый линолеумом бетонный пол не должна составлять менее l4 ≈ 0,7 м. Донышко такой бутылки было снабжено плавным симметричным выступом, выполненным из эпоксидной смолы. Высота водяного столба в ней составляла 10 см. Понятно, что использование материалов с вязкоупругими характеристиками приводит к увеличению потерь энергии при соударении. Тем не менее при свободном падении с высоты от 0,7 до 1,1 м из горлышка бутылки «вырывалась» вода, достигавшая потолка на высоту 3 м.

Таким образом, если в поле тяжести диаметр капиллярной трубки всегда меньше гравитационной постоянной 4 мм, то при свободном падении масштаб проявления капиллярных сил существенно возрастает по меньшей мере на порядок.

Заключение

В рамках упругих моделей жидкости и твердого тела объяснен механизм формирования, напоминающего струю симметричного всплеска воды, образующегося при ударе свободно падающего цилиндрического сосуда о достаточно жесткую горизонтальную поверхность. Получены оценки параметров процесса, которые соответствуют результатам опытов и экспериментов. Показано, что поперечная «пуассонова» деформация, бегущая в стенке заполненного сосуда со сверхзвуковой по отношению к жидкости скоростью, генерирует в ней сходящуюся цилиндрическую волну. Показано что над сосудом поднимаются частицы жидкости которые в момент удара отрываются от свободной поверхности в результате отражения плоской и цилиндрической волн сжатия. Показано, что конфигурация этой поверхности не является установившейся. Экспериментально подтверждено увеличение масштаба проявления капиллярных сил при свободном падении сосуда.