О методе верификации бизнес-процессов с применением сетей Петри

Обеспечение повышения эффективности организационно-управленческой и производственно-технологической видов деятельности является актуальной, но не имеющей в настоящее время однозначного решения задачей.

Следует отметить, что методы формализации и моделирования, известные и применяемые в настоящее время для решения задачи повышения эффективности производственной деятельности, имеют существенные отличия для организационно-управленческих и производственнотехнологических функций.

Данные отличия обусловлены тем, что производственно-технологическая деятельность, в силу своего дискретного характера, может быть формализована в большей мере, нежели организационноуправленческие функции. В самом деле, критерии оценки качества производ- ственно-технологической деятельности, как правило, имеют количественный характер, при этом отношения и зависимости между факторами и показателями в такой деятельности могут быть выражены в виде функциональных зависимостей. При этом показатели организационноуправленческой деятельности не могут быть сведены исключительно, например, к количественным показателям трудозатрат или к показателям финансовых затрат, связанных с исполнением организационно-управленческих функций. С другой стороны, оценка трудозатрат, приведенная к некоторой абстрактной единице результата работ, полученного в ходе исполнения набора организационноуправленческих функций (то есть центру затрат) может служить важным показателем в системе оценивания эффективности труда персонала. В данном случае важную роль играет выстраивание «правиль- ных» наборов деловых операций, которые позволяют получить однозначные результаты работы в виде некоторых наборов сведений, не имеющих количественной оценки. Очевидно, что экспериментирование с наборами деловых операций в реальном режиме времени с целью обнаружения оптимальных последовательностей таких операций является затруднительным, а подчас и невозможным по различным причинам. Известно, что для решения задач оптимизации связанных работ успешно применяются методы имитационного моделирования. Однако для проведения имитационных экспериментов над наборами работ необходимо выполнить некоторую предварительную подготовку. Во-первых, исследуемый набор работ должен быть представлен в виде сетевой модели (например, в виде ориентированного однодольного графа работ, иначе орграфа). Во-вторых, элементы такой сетевой модели должны иметь количественные характеристики, например в виде метрик весов взвешенного орграфа. Полученная таким образом модель набора работ может быть исследована по известным методикам с целью установления, например, критического пути орграфа, ранних и поздних сроков работ и т.д. Сетевые модели, построенные по принципу n-дольного орграфа, могут отражать другие характеристики набора работ. Например, орграф, отражающий набор работ в виде совокупности элементов определённого типа (например, потоков, истоков, стоки в так называемой модели системы массового обслуживания) позволяет в ходе имитационного моделирования выяснить задержки и размеры возникающих очередей в процессе «работе» такой модели. Другими словами, модели орграфов работ, являясь графоаналитическим средством исследования наборов работ, позволяют математически точно и формальным образом вычислять характеристики хода исполнения наборов работ. При этом должны быть выполнены некоторые условия, во-первых, модель орграфа таких работ должна содержать полный набор количественных показателей весов для всех дуг графа, во-вторых, в орграфах должны иметь место равновероятные пути. В противном случае, процедуры исследования наборов работ будут носить эвристический характер, то есть результаты исследования наборов деловых операций будут зависимы от субъективного мнения исследователя, таким образом, полученные результаты нельзя будет назвать однозначными. Например, невозможна не эвристическая оптимизация последовательности работ в наборе работ, где одни работы связаны с другими не хронологическим образом, а посредством результатов, то есть имеет место ситуация, при которой выход одной из работ является входом для другой работы. В данном случае набор только количественных показателей работ не может в полной мере отразить результативность выполняемых деловых операций. Как известно, для отражения именно таких ситуаций применяются процессные модели. Процессные модели, предназначенные для описания наборов деловых операций, называются бизнес-процессами. Следует отметить, что модели бизнес-процессов также являются орграфами, в которых дуги отражают не работы, но связи между работами, при этом связи могут иметь различный смысл и назначение. В настоящее время процессное моделирование является общепринятым способом графического представления организационноуправленческой деятельности [1]. Однако с точки зрения верификации процессных моделей, то есть исследования моделей бизнес-процессов с точки зрения их соответствия реальному положению дел или исследования бизнес-процессов с точки зрения их оптимизации графического способа моделирования процессов недостаточно. В данном случае необходимо применение формальных аналитических методов исследования, которые позволят получить математически обоснованные и однозначные характеристики результатов исполнения деловых операций, организованных в виде процессных моделей.

Как известно, для построения статических структурных моделей процессов применяются графические методы процессного моделирования, в том числе метод SADT/IDEF0 [1, 3]. Структурнофункциональный метод SADT позволяет представить процесс в виде графической схемы, включающей операции процессов, а также связи между операциями, ассоциированные с процессными объектами (например, исполнителями операций, средствами исполнения операций, данными, событиями и т.д.). Известно также, что SADT-модели не отражают ни последовательности, ни хронологии исполнения операций процессов, а также не описывают порядок исполнения процессных операций в случае альтернативных вариантов развития событий. Тем не менее связи между функциями структурнофункциональной модели представляют собой информационный поток преобразования входов процесса в выходы процесса. Заметим, что в статических SADT-моделях отсутствуют способы формальной проверки неразрывности и целостности таких информационных потоков. В целях исследования неразрывности процессных информационных потоков в настоящей работе предлагается исследовать последовательность исполнения операций процессов посредством применения других, более пригодных графоаналитических методов – сетей Петри [2, 4]. Аналитический аппарат сетей Петри предназначен для проведения имитационных экспериментов над процессными моделями, полученными в результате преобразования структурных моделей в сетевые модели по определённым правилам. Исследование процессов с применением сетей Петри позволяет аналитическим образом выявить возможность достижения определённых состояний или, иначе, «выходов» процессов, при заданной структуре процесса. Заметим, что входами и выходами процессных операций могут являться в том числе и факты наличия отношений, в которых находятся процессные объекты. Таким образом, применение методов имитации процессов, которые позволили бы в ходе имитации оперировать отношениями на множестве процессных объектов, обеспечило бы возможность проверки всей совокупности отношений на её пригодность для целей достижения конечных результатов процесса.

С одной стороны, известные и приме- няемые для целей имитации хода исполнения процессов модифицированные (высокоуровневые) сети Петри [2] не позволяют оперировать отношениями между процессными объектами.

С другой стороны, в настоящее время отсутствуют методы моделирования процессов, которые позволили бы представить процесс совокупностью изменяемых в ходе процесса упорядоченных наборов сведений о процессных объектах (иначе, отношений) и при этом обеспечили бы возможность проверки полученных информационных моделей с применением аналитических методов.

В настоящей статье рассматривается построение процессной модели, представленной множеством процессных объектов и отношений на множестве таких объектов. Для целей формального описания отношений на множестве процессных объектов применяется логика предикатов первого порядка. Работа состоит из двух частей: в первой части рассматриваются виды отношений на множестве процессных объектов, имеющих место в процессных SADT-моделях. Во второй части исследуется применимость сетей Петри для целей экспертной верификации процессных молей как множества отношений на множестве процессных объектов.

О представлении процессных объектов в предикатной форме

Под процессными объектами будем понимать данные, предметы, исполните- лей процессных операций, средства исполнения операций, а также события. Процессные объекты ассоциируются со связями (дугами) между процессными операциями [1]. Например, в процессной модели на рисунке 1 процессные объекты отображаются дугами с наименованиями деталей, узлов, исполнителей (например, сборщиков и тестировщиков узлов), а также наименованиями событий – сведениями о результатах тестирования узлов.

В соответствии с правилами SADT [1, 3] граничные связи, например, такие как Требование к порядку сборки и Требование к порядку тестирования (рисунок 1), отвечают за содержание ограничений (например, ограничений на свойства объектов), а также предписаний к выполнению процессных операций. Таким образом, связи «ограничения» и «предписания» отражают условия и процедуры проверки условий соответственно. По этой причине мы не будем включать граничные связи типа «ограничения» и «предписания» в перечень процессных объектов.

Заметим, что в SADT-моделях могут иметь место ситуации, при которых выход одной операции служит требованием (ограничением) для другой операции. В указанных ситуациях связь объектов также будет являться одним из процессных объектов, представляющих собой, например, набор предельно допустимых значе- ний свойств объекта.

Требования к порядку тестирования

Требования к порядку сборки

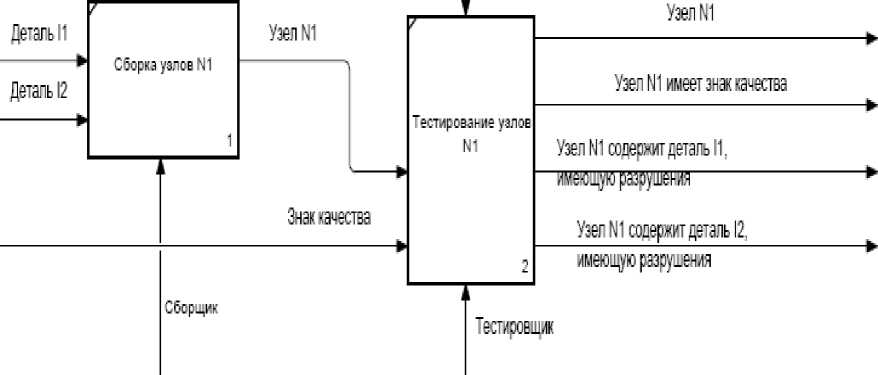
Рисунок 1 – Пример SADT-модели процесса «Сборка узлов»

С одной стороны, SADT-модель процесса представляет собой релевантный реальному процессу (то есть согласованный и прошедший экспертную оценку) набор процессных объектов и операций. С другой стороны, SADT-модель не объясняет порядка выполнения операций, не отражает свойства процессных объектов, а также не показывает сути ограничений по отношению к свойствам объектов. Наиболее важным является то, что графическая SADT-модель позволяет сформировать целостное, системное представление о моделируемой деятельности, выявить процессные объекты, а также обеспечивает возможность установления некоторых видов отношений, в которых состоят процессные объекты.

Рассмотрим виды отношений между процессными объектами на примере типовой SADT-модели процессной операции, которая состоит из следующих эле- ментов (рисунок 2): преобразуемый вход (I1); результат преобразования входа в выход (O1); исполнитель операции преобразования (M1); средство преобразования (M2). Процессные объекты в данном случае вступают в ограниченный набор отношений, как то: «I1 преобразуется в O1»; «M1 обрабатывает I1»; «M1 производит O1»; «M1 применяет M2»; «следствием отношений между I1, M1, M2 является O1». Возможны также отношения «M2 включает M21» и «M2 включает M21» в случае разделения связи M2 на составные части. При этом важно отметить, что все указанные отношения имеют пропозициональный характер, то есть семантика каждого из отношений требует соблюдения порядка перечисления объектов, находящихся в таких отношениях. Нетрудно видеть, что изменение порядка следования объектов в описании отношений изменит смысл отношений, следова- тельно, перечисленные отношения отно- сятся к типу асимметричных отношений.

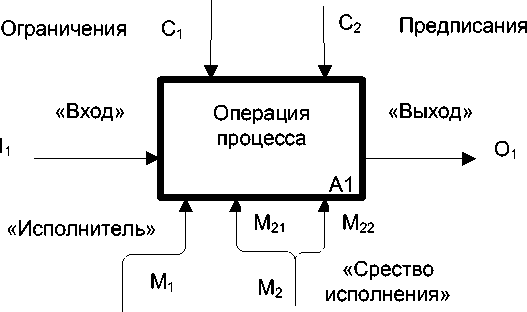
Рисунок 2 – Типовая SADT-модель процессной операции

Перечисленные выше отношения являются следствием применения правил SADT-моделирования. Среди указанных отношений можно выделить следующие виды: функциональные отношения, отношения вида часть – целое, и отношения причинно-следственного характера. Данный перечень отношений можно назвать «типовым» для SADT-моделей, однако такой набор отношений нельзя назвать исчерпывающим. В настоящее время известно множество других видов отношений [8, 9], которые могут иметь место в ходе исполнения операций процесса и представлять собой события – результаты исполнения операций (или процесса в целом). Рассмотрим представление отношений с точки зрения формального описания. Пусть {I,M,O} – множество типовых процессных объектов SADT-модели. Пусть R – множество видов сопоставлений элементов множества {I,M,O}, такое, что: R∈ (IxMxO). Тогда при условии, если R – множество рефлексивных (унарных) или бинарных (или n-арное) асимметричных сопоставлений, то формальное опи- сание сопоставления будет представлять собой упорядоченные множества или, иначе, кортежи, например: , , , , , , и т.д., где: Ii∈ I, Mi∈ M, Oi∈ O, R∈ (R1, R2,.., Rk). Так как рефлексивное (унарное) отношение – это сопоставление процессного объекта с самим собой, то данный вид отношений будет применяться в дальнейшем для отражения факта наличия у объекта некоторых свойств. Заметим, что унарные отношения не характерны для SADT-модели, однако такой вид отношений является очень важным для целей построения информационной модели процесса. Очевидно, что процессные объекты могут состоять также и в отношениях других видов, например, в симметричных отношениях, которые не требуют упорядоченности элементов при описании отношений, однако мы сделаем акцент на более сложных случаях, предполагающих наличие отношений асимметричного вида.

Таким образом, в SADT-моделях могут иметь место процессные события, представляющие собой факты сопоставления процессных объектов (то есть факты наличия отношений). Такие отношения присутствуют в SADT-моделях в виде наименований дуг, например «Узел N1 имеет знак качества» или «Узел N1 содержит деталь I1, имеющую разрушения» (рисунок 1). При этом в SADT-моделях отсутствуют способы формального отражения таких отношений, а также способы формальной проверки адекватности таких отношений конечным результатам процесса в целом. Для целей более детального отражения процессных объектов, в том числе процессных событий в виде отношений и проверки таких отношений на достаточность с точки зрения достижимости результатов процессов, необходимо применение других моделей и средств моделирования.

Применение сетей Петри для проверки неразрывности информационного потока в процессных моделях

Как известно, сеть Петри является графоаналитическим методом исследования распределённых и параллельных процессов [4]. Графическая часть метода представлена двудольным графом с обозначенным исходным состоянием процесса в виде размещения меток в определённых позициях графа (иначе, так называемая «разметка сети»). Аналитическая часть метода содержит формальное описание правил вычисления последующих состояний сети на основании исходных состояний сети, а также на основании известной структуры сети. В настоящее время задача преобразования структуры процессных моделей SADT(IDEF0) в сети Петри с однотипными метками в позици- ях сети достаточно хорошо изучена [5, 7] и не составляет известных проблем. Разметка сети в данном случае означает факты свершения событий, соответствующих наименованиям позиций сети. Наименования позиций сети Петри, в свою очередь, соответствуют наименованиям входов и выходов в SADT-модели процесса. Таким образом, в двудольном графе сети Петри позициям сети соответствуют процессные объекты, переходам сети – операции процесса. Известно, что если переходы Петри сети включают функции преобразования данных, например, логические функции и при этом содержание выходных позиций таких переходов функционально зависит от содержания входных позиций, то такие сети относятся к типу «раскрашенных» сетей [4, 2]. Содержание позиций в раскрашенных сетях Петри описывается метками различных типов. При преобразовании процессной SADT-модели в сеть Петри типу метки в раскрашенной сети соответствует набор сведений о процессном объекте. Как было показано ранее, набор сведений о процессных объектах может быть представлен в виде упорядоченного множества, то есть кортежа. Кортеж формальным образом описывает отношения унарного, бинарного или и n-арного типа. При этом унарные отношения отражают свойства процессных объектов. Бинарные (и n-арные) отношения отражают события, в которых имеет место сопоставление более чем одного процессного объекта.

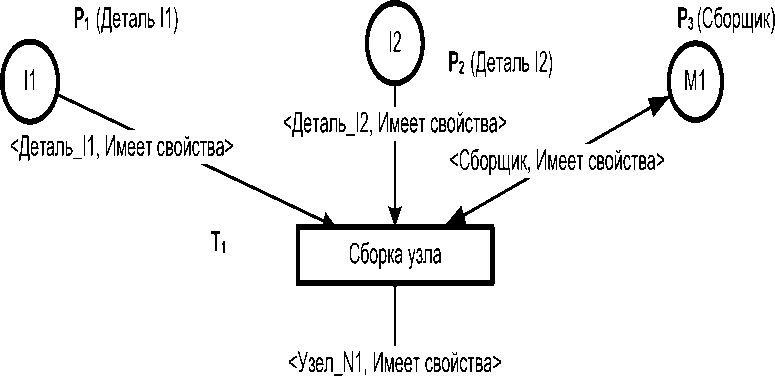
В качестве примера рассмотрим структурно-функциональную модель процесса сборки и тестирования узлов из деталей (рисунок 1). Представим про- цессные объекты на рисунке 1 в виде от-      ношений (то есть кортежей) в таблице.

Таблица – Пример отношений для процессных объектов на рисунке 1

№	Наименование объектов	Наименование отношений	Отображение отношений
1	2	3	4
1	Деталь_I1	Имеет свойства	<Деталь_I1, Имеет свойства>
2	Деталь_I2	Имеет свойства	<Деталь_I2, Имеет свойства>
3	Сборщик	Имеет свойства	<Сборщик, Имеет свойства>
4	Узел_N1	Включает (содержит)	<Узел_N1, Включает, Деталь_I1>
5	Узел_N1	Имеет свойства	<Узел_N1, Имеет свойства>
6	Тестировщик	Имеет свойства	<Тестировщик, Имеет свойства>
7	Знак качества	Имеет свойства	<Знак качества, Имеет свойства>
8	Узел_N1	Имеет оценку	<Узел_N1, Имеет, Знак качества>
9	Деталь_I2	Имеет оценку	<Деталь_I2, Имеет, Разрушения>
10	Деталь_I1	Имеет оценку	<Деталь_I1, Имеет, Разрушения>

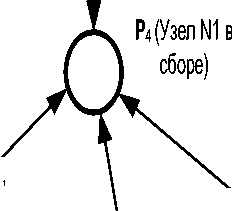
Пример представления SADT-модели процесса «Сборка узлов» сетью Петри приведён на рисунке 3. Начальная разметка сети на рисунке 3 обозначена следующим образом: метки «I1» и «I2» соответствуют фактам готовности деталей; метки «M1» и «M2» соответствуют факту готовности сборщиков и тестировщиков соответственно; метка «*» соответствует факту наличия знаков для подтверждения оценки качества узла. Наименования дуг сетевой модели на рисунке 3 соответствуют содержанию меток в позициях сети и представлены отношениями в форме кортежей (гр. 4 таблица 1). Заметим, что в данном случае применяется одна из модификаций сетей Петри, так называемая высокоуровневая сеть (HLPN) [2].

В соответствии с требованиями правил построения высокоуровневых сетей Петри [2] содержание позиций сети должно соответствовать содержанию входных дуг для данной позиции. Например, представим сеть Петри в виде множества [4]: {Р,T,I,O}, где Р – конечное множество позиций сети; T – конечное множество переходов сети; Р ∩ T = ∅; I – множество дуг вида I : P→T; O – множество дуг вида O : T→P. При этом для раскрашенных сетей Петри входным дугам вида I соответствуют веса WPT, которые отражают содержание меток входных позиций переходов сети, а выходным дугам вида O соответствуют веса WTP, которые отражают содержание меток выходных позиций переходов сети, то есть WPT: P→T и WTP: T→P.

Тогда при {P 1 , P 2 , ..., P n } ∈ P и {T 1 , T 2 , ..., T m } ∈ T, а также при условии, что позиции сети P i и P r связаны одним переходом T k , и при условиях W^PT: P i →T k и W^TP:T k →P r , где (i,r) ∈ n, k ∈ m, будет иметь место зависимость W^PT ∈ W^TP. Применительно к примеру на рисунке 3 это означает, что позиции Р7, Р8, Р9 и Р10 в данной сети Петри не могут быть достижимы, так как веса дуг Т 2 Р 7 , Т 2 Р 8 , Т 3 Р 9 , Т 3 Р 10 не могут быть сформированы по причине несоответствия их весов весам дуг, входящих в переходы Т 2 и Т 7 .

Для устранения проблемы достижи- мости сетевая модель должна быть реор- требований.

ганизована с учетом указанных выше

<Узел_N1 Имеет свойства>

Т2    Тестирование узлов

<Узел_N1,

<Узел_N1,     Имеет свойства>

Имеет свойства>

<Знак качества, Имеет свойства>

Тестирование узлов

<Деталь_I2, Имеет, Разрушения>

P 7

(Деталь I2 имеет разрушения)

P 8 (Узел N1 содержит деталь I2)

<Тестировщик, Имеет свойства>

Т3    Тестирование узлов

<Тестировщик, Имеет свойства>

<Узел_N1, Включает, Деталь_I2>

M2

<Узел_N1, Включает, Деталь_11>

P 6

(Тестировщик)

<Тестировщик, Имеет свойства>

<Узел_N1, Имеет, Знаккачества>

<Деталь_11, Имеет, Разрушения>

P 9

(Деталь I1 имеет разрушения)

(Узел N1 содержит деталь I1)

Ри(Узел N1 имеет знак качества)

Рисунок 3 – Сетевая модель процесса «Сборка узлов»

Другими словами, в структуру сетевой модели на рисунке 3 должны быть внесены дополнительные элементы – позиции и дуги, входящие в переходы Т2 и Т3 дуги, и такие дуги должны иметь веса, содержащие полный набор элементов, необходимых для формирования меток в позициях Р7, Р8, Р9 и Р10. Однако при реорганизации сетевой модели становится очевидным, что полученная сетевая модель не соответствует структуре исходной SADT-модели процесса на рисунке 1 и такую модель следует изменить. Более пригодной структурно-функциональной моделью (с точки зрения информационной полноты) будет служить модель на рисунке 4. Расширенная модель процесса на рисунке 4 включает ранее отсутству- ющие связи между блоками № 1 и № 2, содержащие сведения: «Узел N1 включает деталь I1»; «Узел N1 включает деталь I1»; «Сведения о видах разрушений». Сетевая модель, соответствующая расширенной SADT-модели на рисунке 4, приведена на рисунке 5. Таким образом, правила преобразования SADT-модели к её сетевому представлению послужили средством контроля качества процессной модели с точки зрения информационной полноты.

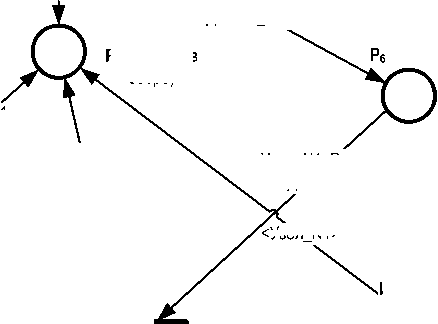
В примере сетевой модели процесса на рисунке 5 за счет позиций P 5 , P 6 , P 7 и соответствующих дуг обеспечивается информационная полнота, необходимая для достижимости требуемых состояний процесса сборки и тестирования узлов.

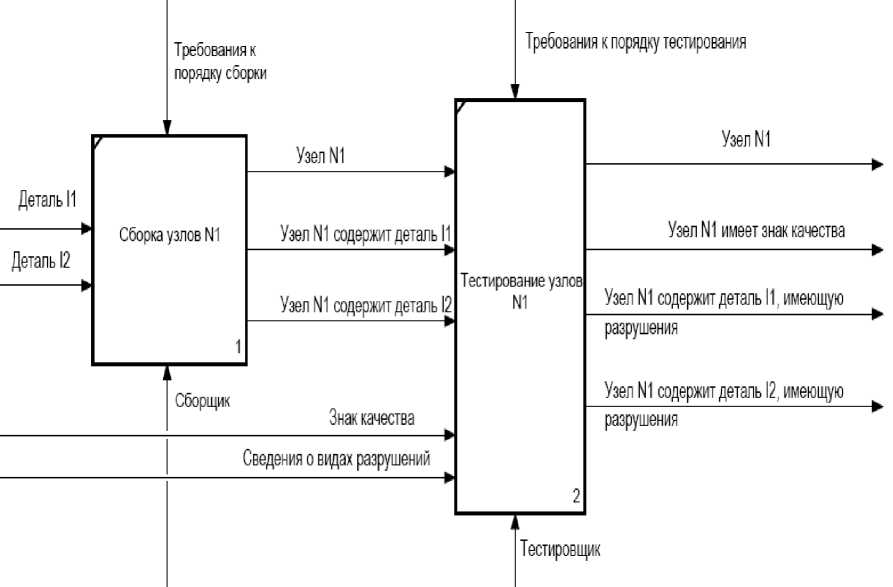
Рисунок 4 – Расширенная SADT-модель процесса «Сборка узлов»

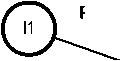
P i (Деталь I1)

<Деталь_11, Имеет свойства>

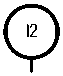
Р 2 (Деталь I2)

<Деталь_12, Имеет свойства>

Р з (Сборщик)

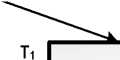
<Сборщик, Имеет свойства>

Сборка узла

<Узел_N1, Имеет свойства>

Р 4 (Узел N1 в сборе)

<Узел_N1, Включает, Деталь_12>

<Узел N1>

<Знак качества, Имеет свойства>

Р 8 (Знак качества)

Т 3

<Разрушение, ' Имеет свойства>

<Узел_N1, Имеет свойства>

_Т Тестирование узлов

<Узел_N1, Имеет свойства>

<Узел_N1, Включает, Деталь_11>

I3

P 7

<Разрушение,

1 Имеет свойства>

<Узел_N1, Включает, Деталь_11>

<Узел_N1, Включает, Деталь_12>

Т 2

Тестирование узлов

<Деталь_12, Имее Разрушения>

<Тестировщик, Имеет свойства>

<Узел_N1, Включает, Деталь_12>

Р 9 (Деталь I2 имеет разрушения)

<Тестировщик, Имеет свойства>

Тестирование узлов

M2

<Тестировщик, Имеет свойства>

(Тестировщик)

<Деталь_11, Имеет, Разрушения>

<Узел_N1, Имеет, Знаккачества>

P i2 (Узел N1 содержит деталь I2)

P 13

(Деталь I1 имеет разрушения)

<Узел_N1, Включает, Деталь_11>

P 11

(Узел N1

имеет знак качества)

P 14

(Узел N1 содержит деталь I1)

Рисунок 5 – Расширенная сетевая модель процесса «Сборка узлов»

Описанный выше метод проверки информационной полноты процессной модели следует отнести к экспертным методам, основанным на правилах построения структуры высокоуровневых сетей Петри.

Заключение

С одной стороны, структурно- функциональные SADT-модели бизнес-процессов позволяют представлять совокупность деловых операций в виде системы, связанных заданной целью элементов процесса: операций, исполнителей, входных и выходных данных для процесса в целом и отдельных операций процесса. С другой стороны, данный метод моделирования не содержит встроенных средств контроля адекватности и полноты сведений, необходимых для достижения результатов (то есть выходов) отдельных операций и процесса в целом). Оценивание достаточности и полноты модели бизнес-процесса предполагается выполнять неформальным образом, посредством привлечения экспертов, например одного из участников бизнес-процессов. Моделирование бизнес-процесса в виде сетей Петри в данном случае позволяет проверить целостность информационного потока преобразования входов процесса в выходы процесса и позволяет формальным образом выполнить анализ полноты сведений, представленных в статической, структурно-функциональной процессной SADT-модели. С одной стороны, очевидно, что вследствие высокой трудоёмкости построения сетей Петри данный метод как таковой не может претендовать на широкое распространение. С другой стороны, данный подход представляет интерес с точки зрения формирования такой полезной структуры сведений о процессных объектах, которая позволит построить логически связанную целостную информационную модель бизнес-процесса, учитывающую не только статические структурные отношения, но и динамические связи и зависимости на множестве процессных объектов.