О МЕТОДЕ ВЫЧИСЛЕНИЯ СВЕТОСИЛЫ В ЭЛЕКТРОННОЙ ОПТИКЕ

В любом измерительном приборе желательно иметь как можно больший выходной сигнал (ток на выходе). Ради этого разработчикам приходится идти на разные ухищрения.

Применительно к энергоанализаторам (ЭА) заряженных частиц (ниже будем рассматривать электроны) как один из возможных путей повышения выходного сигнала рассматривалась возможность увеличения площади поверхности эмиттера, с которого частицы попадают на детектор. Рассмотрим аксиально-симметричную систему (например, цилиндрическое зеркало). Если эмиссия происходит не с оси (радиус-вектор точки эмиссии r ₀ ≠ 0), то в аксиально-симметричном случае площадь эмиссии представляет собой кольцо некоторой толщины с центром, находящимся на оси системы. Если толщина кольца постоянна, а меняется радиус кольца r ₀ , то с ростом r ₀ площадь кольца эмиссии (КЭ) растет пропорционально r ₀ .

В этом месте следует определить понятие светосилы. Рассмотрим ток, который выходит из некоторого малого участка эмиттера и попадает на детектор.

В общем случае [1] светосила некоторой (бесконечно) малой площади эмиттера d s при определенной энергии E — это отношение тока, вышедшего с этой площади и попавшего на детектор ( d I _det ), к полному току, эмитированному с этой площади (d I _em):

S w = d I det d I em .

Если считать распределение плотности эмиссии по углам изотропным, то выражение для светосилы упрощается

S w = d Ω Ω , где d Ω — телесный угол, все электроны, вылетевшие в пределах которого, попадают на детектор; Ω — полный телесный угол 4 π .

Это отношение в [1] названо геометрическим фактором.

При умножении площади выделенного малого элемента КЭ на плотность эмиссии и на величину светосилы получаем ток электронов в пространстве детектора, вылетевших с рассматриваемого элемента поверхности эмиттера.

Основной вклад в теорию функционирования цилиндрического зеркала внесли работы [2–5].

В данной работе рассмотрим вопросы вычисления телесного угла (ТУ) d Ω .

Общие идеи применим к вычислению светосилы цилиндрического зеркала (ЦЗ).

ПОСТРОЕНИЕ ТЕЛЕСНОГО УГЛА

Рассмотрим геометрию цилиндрического зеркала (см. рис. 1). Эмитирующей поверхностью служит плоскость, перпендикулярная оси L системы.

Ввод заряженных частиц в дисперсионное пространство, а затем вход в пространство детектора осуществляется через идеальную сетку, являющуюся частью поверхности внутреннего цилиндра. Конкретные вычисления проводились для ЦЗ с диаметром внутреннего цилиндра r ₁ = 20 мм, диаметром внешнего цилиндра r ₂ = 50 мм.

Методика построения телесного угла приведена в работе [6]. В данной работе мы только вкратце коснемся этого вопроса. Для задания ТУ d Ω применяется задание его границ.

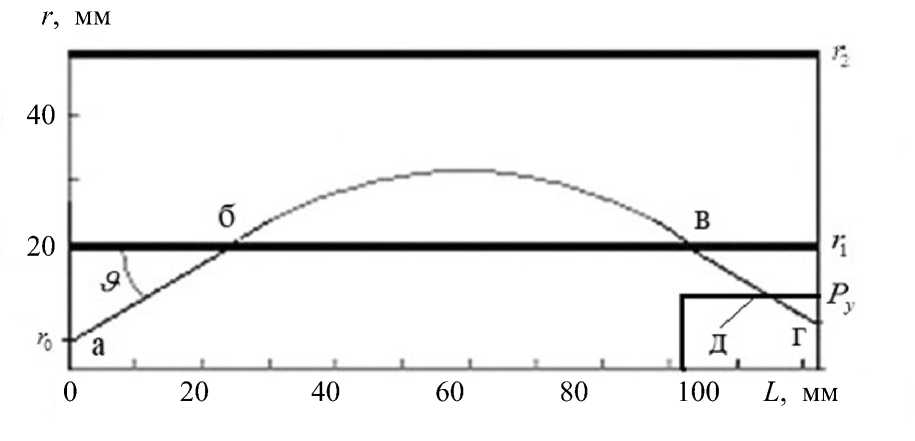
Рис. 1. Половина сечения цилиндрического зеркала (от оси и выше вдоль радиуса) плоскостью, опирающейся на ось.

L — ось ЦЗ; r 1 = 20 мм — радиус внутреннего цилиндра; r 2 = 50 мм — радиус внешнего цилиндра; r 0 — точка эмиссии электронов; д — цилиндр, на котором расположена выходная диафрагма (ЦВД); P_y — радиус цилиндра д; абвг — траектория электрона в ЦЗ; θ — стартовый угол наклона траектории к оси ЦЗ. Подробности в тексте

Все электроны, эмитированные с поверхности источника внутри этих границ, попадают в зазор выходной диафрагмы (ВД). Расстояние L вдоль оси Z, на котором электрон пересекает поверхность цилиндра, содержащего ВД (ЦВД), и попадает на детектор, удовлетворяет неравенству L Beg <  L <  L End , где L b eg и L End соответственно положения ближнего и дальнего края ВД. Для построения телесного угла следует построить линии, стартуя с которых электроны попадают в один из краев ВД.

Из работы [6] берем значение энергии старта электронов E = 124.5 эВ, и L Beg = 91.492мм, L _End = 101.492 мм. L B eg и L _End выбирались такими, чтобы исследуемые нами эффекты проявили себя, r ₀ = 2 мм, радиус ЦВД P_y = 7 мм.

Делим расстояние от ближнего края ВД до дальнего на N L = 100 одинаковых частей. Массив линий L[ i_L ] делит ЦВД на части

L[ it ] = LB eg + d L • iL, где d L = (LEnd - LBeg)/ NL — шаг вдоль L; iL — номер линии деления, изменяется от 0 до NL .

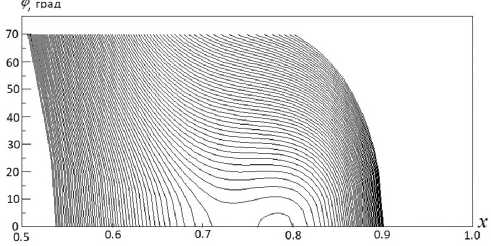
Рис. 2. Вид функции ϕ ( x , L[ i_L ]) при фиксированной энергии E . Подробности в тексте

Для каждой линии L[ i_L ] в соответствии с [6] рассчитываем и строим функцию ф(x , L = L[ i_L ]) (см. рис. 2), где: φ — азимутальный угол; x = = cos( θ ) — косинус угла θ ; радиус старта электронов с поверхности источника r ₀ = 2 мм; радиус цилиндра, содержащего ВД, P_y = 7 мм.

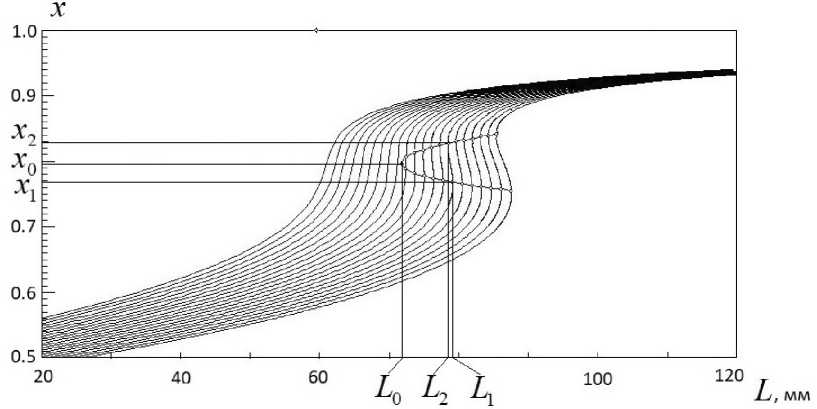
Рис. 3. График функции x = x ( L ) при разных значениях энергии E .

Подробности в тексте

Для каждой части ВД от L[ i_L ] до L[ i_L + 1] на графике функции ϕ ( x ) пространство между двумя линиями ф(x ,L[ i_L ] ) и ф ( x ,L[ i_L + 1]) представляет собой телесный угол. Все электроны, испущенные между линиями ф ( x ,L[ i_L ]) и ффx ,L[ i L + 1]) , попадают в зазор ВД между L[ i_L ] и L[ i_L + 1].

Вид функции ф ( x ,L[ i_L ] ) , приведенный на рис. 2, показывает, что линия ϕ ( x , L[ i_L ] ) может иметь как одно, так и три пересечения с осью x . В дальнейшем нам понадобятся координаты этих точек пересечения. Вычисление точек пересечения означает нахождение нулей функции ϕ ( x , L[ i_L ] ) (см. Приложение 1).

Рассмотрим, как меняется вид соседних линий ϕ(x, L[iL]) (и образуемый ими телесный угол) при увеличении расстояния L. Будем считать, что d L является малым. При значениях L, близких к LBeg (см. рис. 2), последовательные линии ф(x,L[iL ]) и ф(x,L[iL +1]) располагаются практически параллельно и образуют некоторую область (телесный угол), назовем ее основной (см. линии слева на рис. 2 и в Приложении 2 обе линии на рис. П1). Затем при некотором значении L = L2, справа от основной области, появляется малая область. Назовем эту область дополнительной (см. рис. П2 Приложения 2). Точку L2 нанесем на график x = x(L) (см. рис. 3, верхний ряд точек). При дальнейшем увеличении L дополнительная область начинает расширяться: сторона малых зна- чений x в сторону меньших x и основной области, а сторона больших x в сторону больших x. При некоторых значениях L основная область и дополнительная область соприкоснутся и основная и дополнительная области сольются в одну основную область.

Рассмотрим поведение точек пересечения линий ϕ ( x ) с осью L (при разных значениях L и фиксированной энергии E ). Как видно из рис. 2, при значениях L , меньших некоторого значения, линии ϕ ( x ) имеют только одну точку пересечения с осью L .

При значении L = L 2 на графике ф ( x ) появляется точка ( x ₂, L ₂) (справа от основной области), которая при дальнейшем увеличении L переходит в дополнительную область. При увеличении L график функции ϕ ( x ) пересекает ось L уже в двух точках: слева от x ₂ и справа (при x , меньших x ₂ и больших x ₂ ).

При дальнейшем увеличении L лежащая на оси L точка основной области движется в сторону больших x , а ближний край дополнительной области двигается в сторону меньших значений x . В некоторой точке при L = L 1 эти линии соприкоснутся. Поведение точек пересечения линий ϕ ( x ) с осью L показано на рис. 3.

На рис. 3 в диапазоне изменения энергии от E Beg = 124.5 эВ до E End = 129.5 эВ, с шагом d E = 0.25 эВ представлены результаты вычисления функции x = x ( L ).

Основные точки, которые определяют поведение функции x = x ( L ): в точке ( x 2 , L 2 ) появляется дополнительная область, в точке ( x ₁, L ₁) основная и дополнительная области соприкасаются. В точке ( x ₂ , L ₂ ) имеется экстремум (минимум) функции L = L ( x , E = const), т.е. в этой точке имеется фокус первого порядка. На рис. 3 траекторию этой точки в переменных ( x , L ) составляет верхний ряд точек. В точке ( x ₁, L ₁) имеется максимум функции L = L ( x , E = const), т.е. в этой точке также имеется фокус первого порядка. Траектория этой точки составляет нижний ряд точек. В точке ( x ₀ , L ₀) два экстремума сливаются и получается фокус второго порядка.

Было отмечено, что максимальное значение светосилы наблюдается, когда основная и дополнительная области на графике функции ф(x , L = L[ i_L ]) касаются, что соответствует точке ( x 1 ,L 1 ) на графике функции L = L ( x , E = const). Эта точка является точкой фокуса первого порядка.

Таким образом в случае учета неаксиальных траекторий существует область (точка), в которой реализуется фокусировка второго порядка.

ВЫЧИСЛЕНИЕ ТЕЛЕСНОГО УГЛА

Выше был задан диапазон изменения длины вдоль поверхности цилиндра, содержащего ВД, ( L _Beg , L _End ), в пределах которого нам интересно распределение электронов по поверхности этого цилиндра. Этот довольно широкий диапазон первоначально был определен в работе [6]. Аналогично задаем диапазон изменения переменных x ( x _Beg, x _End) и φ ( ϕ _Beg, ϕ _End). Для каждой переменной задаем число разбиений соответствующего диапазона на участки-отрезки N_L , N_x , N _ϕ . И получаем шаг вдоль соответствующей переменной: d L = ( L End - L Beg ) / N l , d x = ( x End - x Beg ) / N x , ^d Ф = C ^ End ^- Ф вeg ^{)/ N} ф .

Из всех пар линий ϕ _B,E ( x ) можно выделить несколько типов (см. Приложение 2) в зависимости от значений индекса — числа пересечений нижней и верхней линий с осью x .

Для вычисления "площади" между двумя последовательными линиями ϕB(x) и ϕE (x) будем использовать метод квадратур Гаусса [7] (метод наивысшей алгебраической точности). Чтобы применять этот метод, линии ϕB,E (x) не должны содержать изломов и сингулярностей, а также участков вблизи сингулярностей (2N – 1 гладкость границ, где N — порядок квадратуры). Будем использовать квадратуры 10-го порядка.

На рис. 2. такими негладкими не подходящими для интегрирования участками могут быть участки линий ϕ _{B, E} ( x ) вблизи пересечения этих линий с осью x , где эти линии могут быть практически перпендикулярными оси x . Поэтому на этих участках проводим интегрирование не по переменной x , а по переменной ϕ .

Рассмотрим первый участок на рис. П1, простирающийся от x _B = x _min до x _E = xCr_B[0] - d x , где xCr_B[0] — x -координата первой точки пересечения линии ϕ _B ( x ) и оси x (определена в Приложении 1). В качестве x min выбираем x min = 0.5, что соответствует углу θ = 60°.

Делим этот участок на N 1 = = int(( x _E - x _B)/ d x ) + 1 частей (отрезков), где int — функция вычисления целой части от некоторого числа. Массив линий, делящих рассматриваемый участок, определяется формулой x[ n ] = = x _B + n • d x . В пределах каждого отрезка (x[ n ], x[ n + 1]) проводим численное интегрирование по правилу Гаусса. Согласно этому правилу, для каждого узла x[ i g ] = x[ n ] + xg[ i g ] • d x методом, описанным в [6], находим значения функций ϕ _B ( x ) и ϕ _E ( x ) на нижней и верхней линиях.

Формула Гаусса для отрезка (x[ n ], x[ n + 1]):

S i [ n ] = ^TAg[ i g ] • ( ф E [ i g ] - ф_в[ i g ] ) , i g = 0

где S 1 [ n ] — вклад в ТУ от отрезка номер n первого участка, i g — номер узла Гаусса, xg[ i g ] — массив узлов Гаусса для отрезка (0, 1), x[ i_g ] — массив узлов Гаусса для отрезка (x[ n ], x[ n + 1]), Ag [ i_g ] — массив весов Гаусса. Значения xg[ i g ] и Ag [ i g ] взяты из таблиц монографии [7], φ_E [ i_g ] и φ_B[ i_g ] — значения функций ϕ _B,E ( x ) в узлах квадратуры, т.е. ϕ _E(x[ i_g ]) и ϕ _B(x[ i_g ]) .

Суммируем все вклады от всех отрезков первого участка

N । - 1

s1 = i S1[ n ], n=0

получаем вклад в ТУ от первого участка диафрагмы (L[ i L ],L[ i L + 1]).

Подобным же образом вычисляем вклад от отрезка 3, где линии ϕB, E (x[ig]) проходят вблизи оси x и касаются ее практически под прямым углом. Поэтому на этом участке проводим интегрирова- ние по переменной ф. Для каждого ф[ig ] = ф[n] + +xg[ ig ]' dф    находим значения функции xL, R (φ[ig]) на левой и правой линиях xL, R(ϕ) :

8 з [ n ] = 2 Ag[ i g ] • (X e [ i g ] - X b [ i g ]).

i g = 0

Суммируя все вклады от отрезков 3-го участка, получаем вклад в ТУ от третьего участка

N 1 - 1

S 3 = 2 S 3 [ n ]■ n = 0

Последний участок на рис. П1, имеющий "треугольный" вид, можно интегрировать как по переменной ϕ , так и по переменной x . Отличие этого случая от ранее рассмотренных в том, что одна из сторон, вдоль которой требуется вычислять x или φ , является прямой, параллельной одной из осей. Поэтому на этой прямой x или φ вычислять не требуется, т.к. на ней или x , или φ постоянны. Это сокращает время вычислений. Сравнительное вычисление площади этого треугольного участка интегрированием по переменной ϕ и по переменной x показало совпадение не хуже 5 знаков (значащих цифр).

Собираем все вычисленные части вместе и получаем ТУ, под которым из источника видна ВД в виде (L[ i_L ], L[ i_L + 1]).

Вычисляем ТУ для всех участков длины зазора диафрагмы и получаем функцию, пропорциональную распределению электронов по длине цилиндра, содержащего ВД.

Все другие возможные случаи конфигурации ТУ, показанные на рис П1–П5, интегрируются вполне аналогично рассмотренному случаю.

На этих рисунках области интегрирования по переменной ϕ показаны (выделены) горизон- тальной штриховкой. Области без штриховки интегрируются по переменной x.

Теперь, с одной стороны, можно вычислить ТУ для любой диафрагмы, размер которой кратен d L . С другой стороны, если построить график S[ i_L ], то получим распределение значений ТУ вдоль цилиндра, содержащего ВД.

РАСПРЕДЕЛЕНИЕ ТУ ВДОЛЬ ЦИЛИНДРА, СОДЕРЖАЩЕГО ВД

Метод вычисления 1

Для получения функции S ( L ) разбиваем выбранный участок ЦВД на N L ( N L = 100) равных частей (L[ i_L ]), строим функции ϕ ( x , L[ i_L ]) и для каждой пары (L[ i_L ], L[ i_L + 1]) вычисляем телесный угол ( S⁽¹⁾ [ i_L ]). Верхний индекс в скобках указывает на то, что это результат первой итерации. Строим график функции S ⁽¹⁾ ( L ) в виде гистограммы рис. 4, где на каждом отрезке (L[ i_L ], L[ i_L + 1]) телесный угол постоянен.

Видно, что график этой функции имеет явно выраженный максимум.

Среди всех S(1) [iL ] находим максимальное значение Sm(1a)x и его номер iL . Выбираем новый участок (L[iL - 2], L[iL + 2]), делим этот участок max                max на NL = 100 частей, находим на нем новые значения S(2) [iL ] и Sm(2a)x . Таким образом, за несколько итераций можно с хорошей точностью вычислить максимум функции и параметры максимума S(L) , т.е. значения S' max, L max, xmax, ( фтах » 0 )■

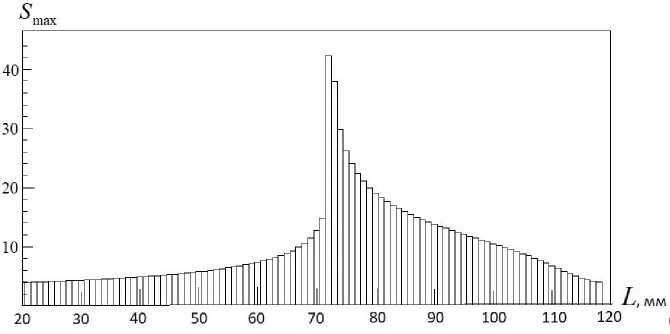
Рис. 4. Вид функции S ⁽¹⁾( L ) при d L = 0.1мм

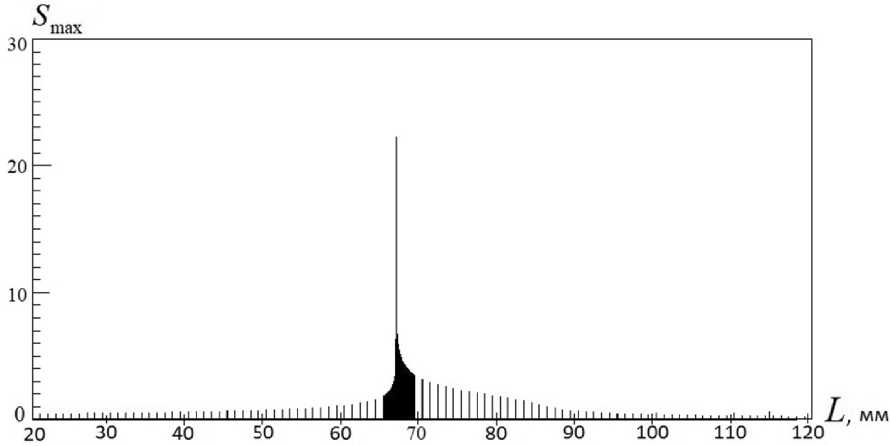
Рис. 5. Вид функции S ( L ) при первых пяти итерациях

У этого метода есть недостаток: результаты разных итераций нельзя представить в виде одной линии (огибающей вершин), т.к. масштабы по S разные.

Метод вычисления 2

Можно к этому вопросу подойти с несколько другой стороны. В предыдущем случае отрезки длины вдоль цилиндра, содержащего ВД, плотно покрывали эту длину. Нам нет необходимости в процессе поиска максимума ТУ знать величину этого ТУ. Достаточно знать величину ТУ относительно соседних участков.

В этом случае нет необходимости плотно покрывать длину цилиндра. Как ранее, разбиваем участок на ЦВД на N_L = 100 равных частей ( L[ i_L ]). Берем некоторую ширину Δ L настолько малой, что при всех итерациях разница L[ i_L +1] - L[ i_L ] была много больше этой ширины. Для образования зазора ВД, по которому будем проводить интегрирование, берем каждое L[ i_L ] и отступаем от него в сторону меньших и больших значений длины на Δ L / 2 . Для этой ширины зазора проводим все вычисления. При этом в любой итерации масштаб по S будет одним и тем же.

Некоторая проблема в масштабе по L. Если при переходе к следующей итерации этот масштаб не менять, то уже вторая, третья и все последующие итерации на графике S(L) сольются (см. рис. 5). Однако хвосты пика будут хорошо видны.

На рис. 5 приведены результаты расчетов функции S ( L ) в каждой из пяти проделанных итераций.

О сокращении времени расчетов

И в заключение этого раздела опишем, как сэкономить время расчетов. Для этого следует применить метод поиска максимума по пяти точкам. Интервал L , в котором предполагается нахождение максимума, делится на четыре равных отрезка. В 5 точках деления вычисляется S ( L ) и среди них находится максимальное значение S ( L ) . Ближайшие 2 отрезка делятся пополам, и в точках деления вычисляются значения S ( L ) . Этим к максимальному значению и 2 точкам, ближайшим к точке с максимальным значением, прибавляются еще 2 точки. Всего снова получается 5 точек. Среди них находим точку с максимальным значением S ( L ) . И так далее. Итерационный процесс можно заканчивать, когда, например, разница между двумя значениями S ( L ) в последовательных итерациях окажется меньше 10^–6. Этот метод нахождение максимума функции S ( L ) оказывается значительно более быстрым, чем описанный ранее.

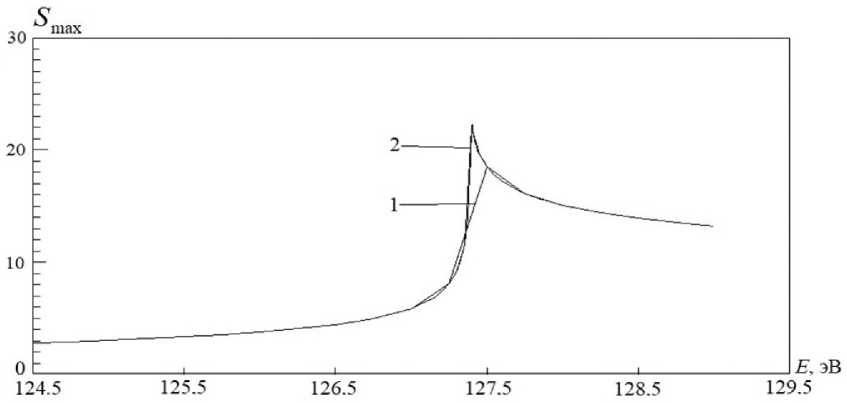
Рис. 6. Вид функции S _max ( L _max, E ) для нескольких итераций по E. 1 — результат первой итерации, 2 — результат пятой итерации

ОБ ОПТИМИЗАЦИИ

В предыдущем разделе было найдено расстояние L _max вдоль оси системы, при котором реализуется максимально возможное значение телесного угла S max . Это было проделано при E 0 = const, r₀ = const, P y = const.

Перед нами стоит задача получить максимальный ток на детекторе. Для этого следует получить максимальный исследованный выше телесный угол. Это задача оптимизации, а целевая функция — телесный угол.

Из [6] берем диапазон значений E0 = (EBeg, EEnd), в рамках которого имеет смысл искать максимальное значение S . Разбиваем max этот диапазон на    Ne    поддиапазонов

(dE = (EEnd - EBeg)/Ne ) и при Ne + 1   значени ях энергии (EiE = EBeg + d E • iE) вычисляем Smax максимальное среди всех значений L и заодно получаем Lmax , при котором этот максимум реализуется. Результаты такого действия приведены на рис. 6 (линия 1).

Каждая точка этого графика соответствует определенной энергии E и представляет собой максимальное значение ТУ при этой энергии. Далее находим максимальное значение по E , используя такой же алгоритм, что был использован при нахождении максимума по L . То есть находим максимальное значение E _m⁽¹_a⁾_x в первой итерации и номер этого значения i_{E max} . Далее уточняем

E _m ^{( i} _a⁾_x по ранее приведенной для L методике. Для этого изменяем диапазон энергии:

^E beg = ^{E [} i E max - ^2] и ^E end = ^{E [} i E max ^{+ 2] .}

В новом дипазоне вычисляем S _max ( L _max , E ) и находим E _m⁽²_a⁾_x и т.д.

Так как мы получили экстремум (максимум) по каждой из переменных ( L и E ), то в этой точке мы имеем локальный максимум. Этот алгоритм очень похож на метод Гаусса – Зайделя (метод покоординатного спуска, или поиск оптимума поочередно по каждой переменной).

Подобные действия проводим для r ₀ е (0, r ) и для P y е (0, r 1 ). Результаты выведены на рис. 7.

На рис. 7 цифра 1 соответствует значению r0 = 0.1 • r, 2 — r0 = 0.2 • r1, 3 — r0 = 0.3 • r, 4 — r0 = 0.4 • r, 5 — r0 = 0.5 • r1, 6 — r0 = 0.6 • r1, 7 — r0 = 0.7 • r, 8 — r0 = 0.8 • r1,9 — r0 = 0.9 • r1.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Ранее было отмечено, что максимальное значение светосилы наблюдается, когда основная и дополнительная области на графике ϕ ( x ) касаются, что соответствует точке ( L ₀, x ₀ ) на графике L ( x ). Находя максимум светосилы при изменении энергии, мы находим точку слияния двух фокусов первого порядка в фокус второго порядка.

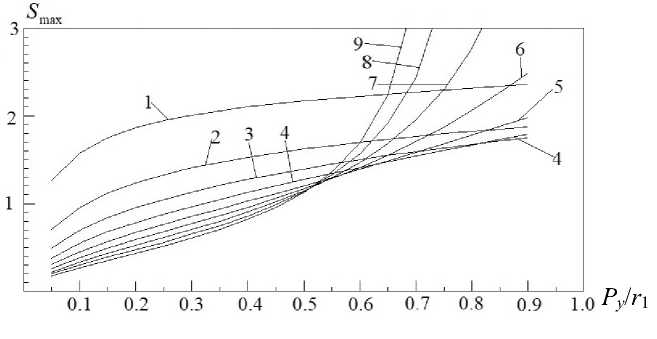
Рис. 7. Зависимость величины максимальной светосилы (оптимизированной по L и E ) от радиуса ЦВД ( P y ), при разных значениях радиуса старта электронов r ₀ .

Подробности в тексте

Табл. Сравнение найденных максимумов

Метод	max	L max , мм
Слияние	0.10184942	96.725138
Оптимизация	0.10144286	96.725174

Для подтверждения этого приведем данные сравнения результатов поиска максимума светосилы методом оптимизации и только что описанным методом (см. табл.).

Описанная выше методика нахождения максимума светосилы не может обеспечить значительную точность. Хотя приведенные данные показывают весьма неплохие результаты. С другой стороны, новая методика показала, что требует примерно на 2 порядка меньше счетного времени, чем метод расчета светосилы и ее оптимизация.

Основной результат данной работы показан на рис. 7. Видно, что с увеличением P_y максимально достижимая светосила растет. А вот зависимость максимально достижимой светосилы от радиуса старта электронов с поверхности эмиттера не столь однозначна.

При P y <  0.4 • r 1 и при увеличении r ₀ S max уменьшается. Причем при приближении r ₀ к r ₁ наблюдается сгущение линий S _max ( P_y / r ₁) .

До r ₀ <  0.3 • r 1 и для всех P y линии S _max с большими номерами всегда располагаются ниже линий с меньшими номерами. Начиная с линии с номером 4, которая пересекает линию с номером 3 примерно при P y = 0.8 • r 1 , все последующие линии

S _max пересекают все предыдущие линии. Наблюдается точка сгущения, в которой пересекаются линии с номерами от 5-го до 9-го.

Линия 6 при больших P_y пересекает линию 1. То есть полный сигнал при r ₀ >  0.5 • r 1 и P y >  0.85 увеличивается по отношению к величине сигнала с площадки вблизи оси на отношение площадей эмиссии.

Гораздо более интересны графики S _max с номерами с седьмого по девятый, линии на которых уходят за верхнюю границу рисунка. Этот режим будет нами рассмотрен в следующей работе.

ПРИЛОЖЕНИЕ 1.

ВЫЧИСЛЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ЛИНИИ ϕ ( x ) И ОСИ X

Вычисление точек пересечения означает нахождение нулей функции ф(x , L = L[ i_L ]).

Первый этап решения уравнения

ф ( x , L = L[ i_L ]) = 0                   (П1)

заключается в нахождении интервала х , в котором функция ф ( x , L = L[ i_L ]) меняет знак. Для этого весь интервал изменения х делим на N_x равных частей. В точках деления находим значение функции ϕ ( x , L[ i_L ]) и последовательно проверяем все отрезки оси х на выполнение одного из неравенств:

Ф (х[ n ]) <  0 <  ф (х[ n + 1])                    (П2)

или ф (x[ n +1]) < 0 < ф(х[ n ]). (П3)

Этим мы локализовали положение одного из корней уравнения (П1).

На втором этапе вычисляем более точное значение искомого корня методом деления пополам (метод пристрелки). Для удобства введем обозначения x[ n ] = x 1 , x[ n + 1] = x 2 , ф(x 1 ) = y 1 , ф(x 2 ) = y 2 . Как выше было отмечено, y 1 и y 2 имеют разные знаки. Берем точку x m = 0.5 • ( x , + x 2 ) и вычисляем в ней У т = Ф ⁽ x m )•

Проверяем совпадение знаков:

если y 1 • y m <  0 (т.е. они имеют разный знак), то проводим замену x 2 = x m , y 2 = y m и далее берем среднюю точку x m и вычисляем y m = ф ( x m ) и т.д.

Если y , • y m >  0 (одинаковый знак), то проводим замену x = x m , y , = y m , берем среднюю точку x m и вычисляем y m = ф ( x m ) и т.д.

Эту процедуру повторяем, пока абсолютная величина y m не станет меньшей 10 - 8 . Это значит, что с этой точностью корень найден.

Вводим параметр xCr[0] = x m — x- координату первой точки пересечения линии φ ( x ) и оси x.

Первый корень мы нашли. Далее проверяем следующие промежутки x е (x[ n + 1], x[ n + 2]) на наличие на них корня. Введем целое число nCr — признак, указывающий, сколько пересечений имеет линия ϕ ( x , L[ i_L ]) с осью x .

Если на одном из следующих отрезков x выполняется неравенство (П2) или (П3), то на рассматриваемом участке есть еще одно пересечение линии ϕ ( x ) с осью x , которое получаем после применения метода деления пополам. Присваиваем nCr = 2 и xCr[1] = x m .

Согласно рис. 2, если есть второе пересечение линии ϕ ( x ) с осью x , то есть и третье. Нахождение этого пересечения вполне аналогично: nCr = 3 и xCr[2] = x m .

ПРИЛОЖЕНИЕ 2.

ВЫЧИСЛЕНИЕ ТЕЛЕСНОГО УГЛА

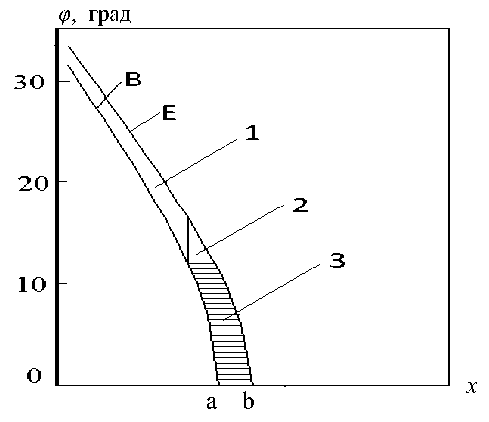
Рис. П1. Телесный угол образует пара соседних линий ф _в = ф ( x , L[ i L ]) и ф _Е = ф ( x , L[ i_L + 1]), для которых nCr = 1. В телесном угле присутствует только основная область, а дополнительная отсутствует.

B — нижняя линия ф _в = ф ( x , L[ i_L ]) пересекает ось x в точке "а"; Е — верхняя линия ф _Е = ф ( x ,L[ i_L + 1]) пересекает ось x в точке "b"; 1 — область интегрирования по переменной х , в которой необходимо рассчитывать ϕ _B и ϕ _E ; 2 — область интегрирования по переменной х , в которой необходимо рассчитывать только ϕ _E ; 3 — область интегрирования по переменной ϕ , в которой необходимо рассчитывать x_L (φ[ i_g ]) и x_R (φ[ i_g ])

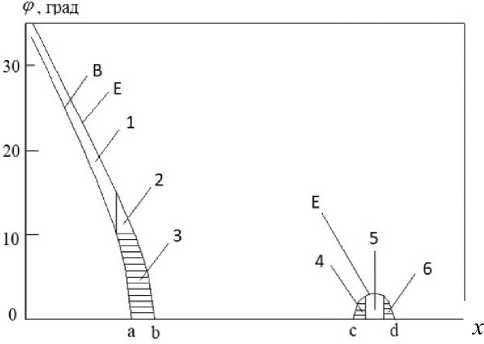
Рис. П2. Телесный угол образует пара соседних линий Ф _в = ф(x ,L[ i L ]) и Ф _Е = ф(x ,L[ i_L + 1]), для ф в nCR = 1 и для φ _E nCR = 2.

Левая часть телесного угла является основной частью и образована линиями B (линия ϕ _B ), которая пересекает ось x в точке "a", и E (линия ϕ _E), которая пересекает ось x в точке "b". Правая часть телесного угла является дополнительной частью и образована только линией E, которая пересекает ось x в точках "c" и "d".

На рисунке обозначения такие же, как на рис. П1, и дополнительно: 4 — область интегрирования по переменной ϕ , в которой необходимо рассчитывать x _B ; 5 — область интегрирования по переменной х , в которой необходимо рассчитывать только ϕ _E ; 6 — область интегрирования по переменной ϕ , в которой необходимо рассчитывать x _E

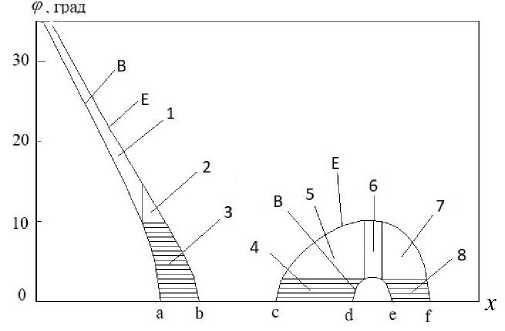
Рис. П3. Телесный угол образует пара соседних линий ф _в = ф ( x , L[ i_L ]) и ф _Е = ф ( x , L[ i_L + 1]), для которых nCR = 2.

Левая часть телесного угла является основной частью и образована линиями B, которая пересекает ось x в точке "a", и E, которая пересекает ось x в точке "b". Правая часть телесного угла является дополнительной частью и образована линиями B, которая пересекает ось x в точках "d" и "e", и E, которая пересекает ось x в точках "с" и "f".

На рисунке обозначения такие же, как на рис. П1, и дополнительно: 4, 8 — области интегрирования по переменной ϕ , в которых необходимо рассчитывать x_L (φ[ i_g ]) и x_R (φ[ i_g ]) ; 5, 7 — области интегрирования по переменной х , в которых необходимо рассчитывать только ϕ _E ; 6 — область интегрирования по переменной х , в которой необходимо рассчитывать ϕ _B и ϕ _E

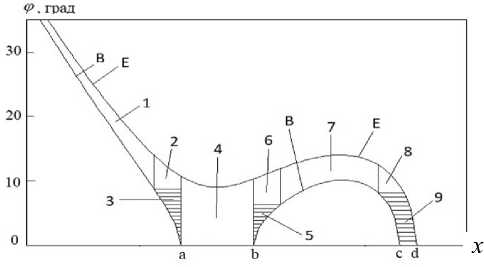
Рис. П4. Телесный угол образует пара соседних линий ф _в = ф ( x , L[ i_L ]) и ф _Е = ф ( x , L[ i_L + 1]), для ф в nCR = 3 и для φ E nCR = 1.

Телесный угол состоит только из основной части, которая образована линиями B (пересекает ось x в точках "a", "b" и "c") и E (пересекает ось x в точке "d").

На рисунке обозначения такие же, как на рис. П1, и дополнительно: 4, 6, 8 — области интегрирования по переменной x , в которых необходимо рассчитывать только ф _в = ф ( x , L[ i_L ]); 5 — область интегрирования по переменной ϕ , в которой необходимо рассчитывать x B = x ( ф ,L[ i_L ]); 7 — область интегрирования по переменной х , в которой необходимо рассчитывать ϕ _B и ϕ _E ; 9 — область интегрирования по переменной ϕ , в которой необходимо рассчитывать x _B и x _E

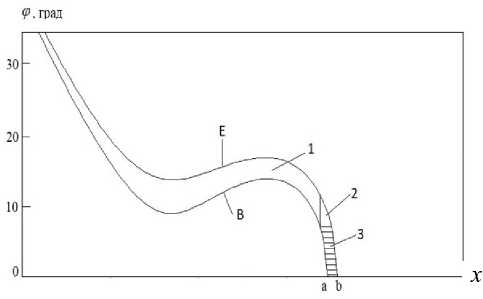
Рис. П5. Телесный угол образует пара соседних линий ф = ф( x, L[ i L ]) и ф _Е = ф( x, L[ i_L + 1]), для которых nCR = 1, т.е. присутствует только основная область. На рисунке обозначения такие же, как на рис. П1