О методике дефаззификации при обработке нечеткой экспертной информации

Автор: Димитров Валерий Петрович, Борисова Людмила Викторовна, Нурутдинова Инна Николаевна, Богатырва Елена Валерьевна

Журнал: Вестник Донского государственного технического университета @vestnik-donstu

Статья в выпуске: 6 (49) т.10, 2010 года.

Бесплатный доступ

Рассматриваются некоторые аспекты методики дефаззификации при обработке нечеткой экспертной информации в экспертной системе для технологической регулировки машин. Приведен пример использования методики.

Лингвистическая переменная, функция принадлежности, дефаззификация

Короткий адрес: https://sciup.org/14249431

IDR: 14249431

Текст научной статьи О методике дефаззификации при обработке нечеткой экспертной информации

Введение. При использовании сложной уборочной техники одной из важных задач является технологическая настройка машины в полевых условиях. Эту задачу можно отнести к классу неформализованных задач принятия решений . Решение задачи возлагается на оператора и зависит от его опыта и квалификации. Трудности с выбором значений регулируемых параметров комбайна связаны с неопределенностью информации о факторах внешней среды, в которой функционирует зерноуборочный комбайн, а также сложностью взаимосвязей между факторами уборки и регулируемыми параметрами.

Основным резервом повышения эффективности использования комбайнов следует считать снижение временных затрат на настройку и технологические простои. Поэтому особого внимания заслуживают вопросы разработки систем информационной поддержки интеллектуальной деятельности оператора при проведении уборочных работ.

Перспективным направлением совершенствования методов технологической настройки машин является разработка информационных систем поддержки принятия решений (экспертных систем) [1].

Методика моделирования процесса принятия решений при технологической настройке комбайна основана на использовании аппарата нечетких множеств и содержит этапы: фаззифи-кации, композиции и дефаззификации [2, 3].

На этапе фаззификации необходимо представить условия решения задачи в лингвистической форме. При композиции все нечеткие множества, назначенные для каждого терма каждой входной переменной, объединяются, и формируется единственное нечеткое множество – значение для каждой выводимой лингвистической переменной. В результате использования набора правил – нечеткой базы знаний – вычисляется значение истинности для предпосылки каждого правила на основании конкретных нечетких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил. Суть дефаззификации заключается в выработке на основе нечеткого логического вывода рекомендаций по установлению конкретных значений регулируемых параметров машины.

Рассмотрим подробно некоторые особенности методики дефаззификации.

Описание предметной области. Решая задачу, когда в зависимости от возможных значений входной ситуации ( А j ) эксперт делает вывод о выходной ситуации ( В j ) (о значениях регулируемых параметров), обозначим через { X } множество значений входных параметров, т.е. совокупность значений факторов внешней среды, существенно влияющих на величину выходного параметра V (регулируемого параметра), и моделируем экспертную информацию об отношениях рассматриваемых признаков, а также процедурах принятия решений.

В соответствии с логико-лингвистическим подходом [1, 2, 4] мы разработали модели входных и выходных признаков X, V в виде семантических пространств и соответствующих им функций принадлежности:

{ X i , Т ( X ) , U, G, M} , ц R ( x_b X 2 , ., x) e (0; 1), (1)

^{P v , T v , V G v , M v ^}, ц R ( v ₁, v ₂, .„, V j ) e (0; 1).

В результате обобщенную модель предметной области «предварительная настройка жатвенной части» представим в виде композиции нечетких отношений изучаемых семантических пространств:

R = X ^ V ,

где R – нечеткое отношение между факторами внешней среды и регулируемыми параметрами,

R { X i , Т ( X i ), U , G , M} x

v , T v , V , G v , M v > V ( x , v ) e X x V .

Отношение R можно рассматривать как нечеткое множество на прямом произведении Х х V полного пространства предпосылок Х и полного пространства заключений V .

Схему решения задачи предварительной настройки рассмотрим на примере выбора значения скорости комбайна. Известно, что на данный параметр влияют такие факторы внешней среды, как урожайность (Ур), влажность хлебной массы (Вл), соломистость (Сол), засоренность (З) [5].

Кортеж лингвистической переменной «Урожайность - 40» имеет вид:

<УРОЖАЙНОСТЬ-40, ц/га {Менее 40, Примерно 40, Более 40}, [34 - 46] >

Ур={УрМ40, УрПр40, УрБ40}.

Кортеж лингвистической переменной «Влажность хлебостоя» имеет вид:

<ВЛАЖНОСТЬ ХЛЕБОСТОЯ,% {Сухой, Нормальный, Влажный}, [0 - 30]> ВлХл={ХлС, ХлНор, ХЛВл}.

Кортеж лингвистической переменной «Соломистость» имеет вид:

<СОЛОМИСТОСТЬ, % {Малая, Нормальная}, [40 - 70]> Сол={СолМ, СолНор}.

Кортеж лингвистической переменной «Засоренность хлебостоя» имеет вид:

<ЗАСОРЕННОСТЬ ХЛЕБОСТОЯ, % {Низкая, Большая}, [0 - 40] > Зхл={ЗХлН, ЗХлБ}.

Кортеж лингвистической переменной «Скорость комбайна для пшеницы-40» (т.е. для значения урожайности примерно 40 ц/га) имеет вид:

<СКОРОСТЬ КОМБАЙНА ДЛЯ ПШЕНИЦЫ–40, км/ч {Очень низкая, Низкая, Ниже номинальной, Номинальная, Выше номинальной, Высокая, Очень высокая}, [2,5 – 5,5] >;

Ск={СкОН, СкН, СкННом, СкНом, СкВНом, СкВ, СкОВ}.

В результате фаззификации исследуемых признаков построены функции принадлежности регулируемых параметров и внешних факторов. При этом для описания крайнего левого терма используется выражение (3), для среднего терма – (4), для крайнего правого терма – (5):

ц( x , a , b )

1, b - x b - a ’

если x < a если x < b если x > b

Ц ( x, a, b, c ) =	0, x - a		если если если если	x < a a < x < c
	c b	- a ^, - x
				c < x < b x > b	(4)
	b	- c ^,0,
ц( x , a , b ) =	x	0, — a	если если	x < a x < b	(5)
	b	- a ’

	.	1,	если	x > b

Значения коэффициентов a, b, c, d функций принадлежности (ФП) для входных параметров приведены в табл. 1, для выходного параметра – скорости движения комбайна , – в табл. 2.

Таблица 1

Значения коэффициентов a, b, c функций принадлежности для входных параметров

Вид терма	Коэффициенты ФП
Вид терма	Ур	Вл	З	С
Левый	a = 34 b = 40	a = 11 b = 14	a = 10 b = 30	a = 45 b = 55
Центральный	a = 34 b = 46 c = 40	a = 11 b = 17 c = 14
Правый	a = 40 b = 46	a = 14 b = 17	a = 10 b = 30	a = 45 b = 55

Таблица 2

Значения коэффициентов a, b, c функции принадлежности для выходного параметра (скорости комбайна)

Вид терма	Кэффициенты ФП для выходного параметра
Левый	a = 2,5 b = 3,0
Центральные	a = 2,5 b = 3,0 c = 3,5	a = 3,0 b = 4,0 c = 3,5	a = 3,5 b = 4,5 c = 4,0	a = 4,0 b = 5,0 c = 4,5	a = 4,5 b = 5,5 c = 5,0
Правый	a = 5,0 b = 5,5

Моделирование вывода решения . При заданной системе логических высказываний для значений входных параметров значениями выходного параметра V является такое множество V 0⁽¹⁾ , для каждого элемента которого и е V 0¹) схема вывода

~ (1)

А' - истинно; (6)

В' - истинно имеет наибольшую степень истинности ц^ нечеткого правила modus ponens:

Ц ^(D = min{1,[1 -ц W ( w ') + ц V ( v ')],...,[1 — ц w ( w ') + ц v ( v ')]} . (7)

11 mm

Величина ц ^ _р ( 1 ) является степенью истинности правила modus ponens для нечеткой системы экспертных высказываний. Данное понятие отражает степень соответствия значения v ' выходного параметра V значению w ' обобщенного входного параметра W при задании экспертной информации нечеткой системой.

Обозначим через A, и B высказывания < р W есть a _Wj > и < р V есть а _Vj >. Тогда система не-

четких высказываний запишется в виде:		< если < если	~ А 1 , ~ А 2 ,	то то	~ B 1 ~ B 2	> ,
~(1) L =■	' ~(1) L 1 : ~⁽¹⁾ L 2 :
						> ,	(8)
	... ~(1)		~		~
	L m :	< если	А т ,	то	B m	>

Нечеткие высказывания соответствуют общей форме:

~ ~

A j : < р W есть a W > и B . : < р V есть а V > ,

W Wj j V Vj где аV ,аV,аV - соответствующие значения термов выходной лингвистической переменной.

В основе механизма вывода решений интеллектуальной информационной системы лежит модель предметной области «предварительная настройка», представляющая собой композицию нечетких отношений семантических пространств факторов внешней среды и регулируемых параметров жатвенной части.

Развернутую форму нечеткого логического вывода для системы знаний вида (8) можно представить так:

И в - = , V I Л и Bkj y j IЛ Л и Aki ⁽ x ' ) . k е K ^ j е J у i е I

В результате анализа предметной области создана база знаний, на которой основан логический вывод решения. Фрагмент базы знаний представлен ниже:

Решение задач с использованием методов нечеткой логики предполагает определение точных значений выходных переменных. На этапе дефаззификации используются различные методы, например, метод «центра тяжести» [4, 6]:

У ‘ = ( J y j Y j ^ в' ⁽ Уз ) dy j ) / ( J ^ в' ⁽ y j Y j ) dy j ) . ⁽¹⁰⁾

Методика и результаты моделирования. Рассмотрим применение методики определения значений регулируемых параметров на основе нечеткого логического вывода.

Для иллюстрации использования методики рассмотрим пять наборов значений входных параметров. В табл. 3 приведены некоторые численные значения входных параметров и используемых правил.

Таблица 3

Исходные данные для расчета

Номер примера	Входные параметры				Номера правил базы знаний
Номер примера	Ур	Сол	З	Вл	Номера правил базы знаний
I	42	48	12	15	14, 15, 17, 18, 20, 21, 23, 24, 26, 27, 29, 30, 32, 33, 35, 36
II	42	52	24	15
III	42	50	10	12	13, 14, 16, 17, 25, 26, 28, 29
IV	36	50	10	12	1, 2, 4, 5, 13, 14, 16, 17
V	36	45	14	10	1, 2, 7, 8, 13, 14, 19, 20

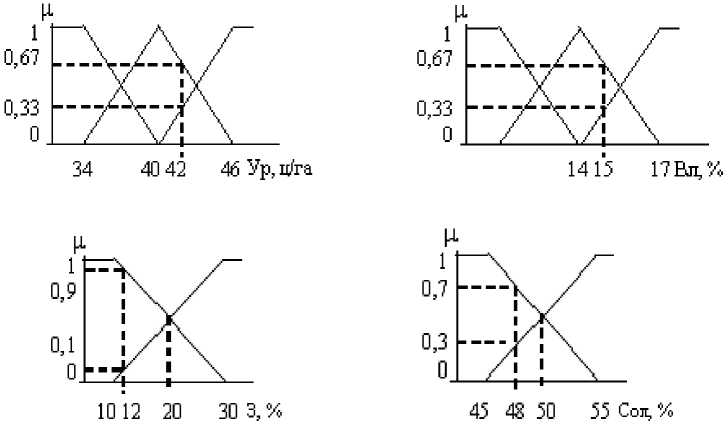
Первый этап. Определение значений функций принадлежностей входных параметров.

Выберем для иллюстрации пример I из табл. 3. Значения функций принадлежностей для рассматриваемых входных факторов вычислены по формулам (3)-(5) с учетом соответствующих коэффициентов (табл. 4) и представлены графически (рис.1).

Рис.1. Вид функций принадлежностей входных факторов и их численные значения для примера I

Значения функций принадлежности

Таблица 4

Скорость	Ур	Сол	З	Вл
Низкая Н	0,67	0,7	0,9	0,67
Высокая В	0,33	0,3	0,1	0,33

Второй этап. Перебор всех комбинаций (в нашем случае их 16) входных параметров и нахождение по правилам значения выходного параметра (скорости комбайна). В нашем случае значениями скорости будут ОН – очень низкая, Н – низкая, НН – ниже номинальной, В – высокая. Затем для каждой комбинации находим минимальное значение функций принадлежности входных переменных. Результаты перебора для примера I приведены в табл.5.

Таблица 5 Промежуточные результаты расчетов для примера I (Ур = Пр40; Сол = низкая; З = низкая; Вл = низкая)

Номер правила	Значения функций принадлежности для входных параметров и значения термов выходного параметра
Номер правила	Ур	Сол	З	Вл	Ск	min
1	2	3	4	5	6	7
14	0,67	0,7	0,9	0,67	ННом	0,67
15	0,67	0,7	0,9	0,33	Н	0,33
20	0,67	0,7	0,1	0,67	Н	0,1
21	0,67	0,7	0,1	0,33	ОН	0,1
17	0,67	0,3	0,9	0,67	ННом	0,3
18	0,67	0,3	0,9	0,33	Н	0,3

Окончание табл.5
1	2	3	4	5	6	7
23	0,67	0,3	0,1	0,67	Н	0,1
24	0,67	0,3	0,1	0,33	ОН	0,1
26	0,33	0,7	0,9	0,67	ННом	0,33
27	0,33	0,7	0,9	0,33	Н	0,33
32	0,33	0,7	0,1	0,67	Н	0,1
33	0,33	0,7	0,1	0,33	ОН	0,1
29	0,33	0,3	0,9	0,67	Н	0,3
30	0,33	0,3	0,9	0,33	ОН	0,3
35	0,33	0,3	0,1	0,67	Н	0,1
36	0,33	0,3	0,1	0,33	ОН	0,1

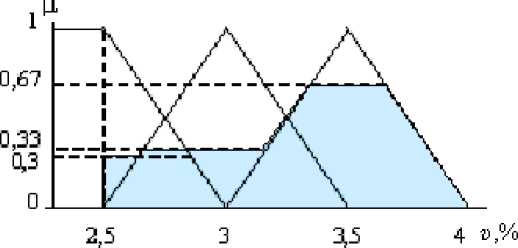
Третий этап. Сортировка всех комбинаций скоростей. Для примера I значения скоростей – ОН (очень низкая), Н (низкая), НН (ниже номинальной), В (высокая). Для каждого из значений скоростей из всех минимумов значений функций принадлежности выбираем максимальное. Полученные максимальные значения наносим на график функции принадлежности выходной переменной – «скорость». Описанную процедуру для рассматриваемого примера I иллюстрируют табл.6-8 и рис.2.

Рис.2. Итоговый рисунок для примера I

Таблица 6

Параметры лингвистической переменной	Значения функций принадлежности для входных параметров и значения термов выходного параметра
Параметры лингвистической переменной	Ур	Сол	З	Вл	min	max (min)
Наименование терма	Н	Н	В	В	-	0,3
Значение ФП	0,67	0,7	0,1	0,33	0,1
Наименование терма	Н	В	В	В	-
Значение ФП	0,67	0,3	0,1	0,33	0,1
Наименование терма	В	Н	В	В	-
Значение ФП	0,33	0,7	0,1	0,33	0,1
Наименование терма	В	В	Н	В	-
Значение ФП	0,33	0,3	0,9	0,33	0,3
Наименование терма	В	В	В	В	-
Значение ФП	0,33	0,3	0,1	0,33	0,1

Таблица 7

Значения термов входных параметров и соответствующих значений функций принадлежности, приводящих к скорости ниже номинальной (ННом)

Параметры лингвистической переменной	Значения функций принадлежности для входных параметров и значения термов выходного параметра
Параметры лингвистической переменной	Ур	Сол	З	Вл	min	max (min)
Наименование терма	Н	Н	Н	Н	-	0,67
Значение ФП	0,67	0,7	0,9	0,67	0,67
Наименование терма	Н	В	Н	Н	-
Значение ФП	0,67	0,3	0,9	0,67	0,3
Наименование терма	В	Н	Н	Н	-
Значение ФП	0,33	0,7	0,9	0,67	0,33

Таблица 8

Значения термов входных параметров и соответствующих значений функций принадлежности, приводящих к низкой (Н) скорости

Параметры лингвистической переменной	Значения функций принадлежности для входных параметров и значения термов выходного параметра
Параметры лингвистической переменной	Ур	Сол	З	Вл	min	max (min)
Наименование терма	Н	Н	Н	В	-	0,3
Значение ФП	0,67	0,7	0,9	0,33	0,33
Наименование терма	Н	Н	В	Н	-
Значение ФП	0,67	0,7	0,1	0,67	0,1
Наименование терма	Н	В	Н	В	-
Значение ФП	0,67	0,3	0,9	0,33	0,3
Наименование терма	Н	В	В	Н	-
Значение ФП	0,67	0,3	0,1	0,67	0,1
Наименование терма	В	Н	Н	В	-
Значение ФП	0,33	0,7	0,9	0,33	0,33
Наименование терма	В	В	Н	Н	-
Значение ФП	0,33	0,3	0,9	0,67	0,3
Наименование терма	В	В	В	Н	-
Значение ФП	0,33	0,3	0,1	0,67	0,1

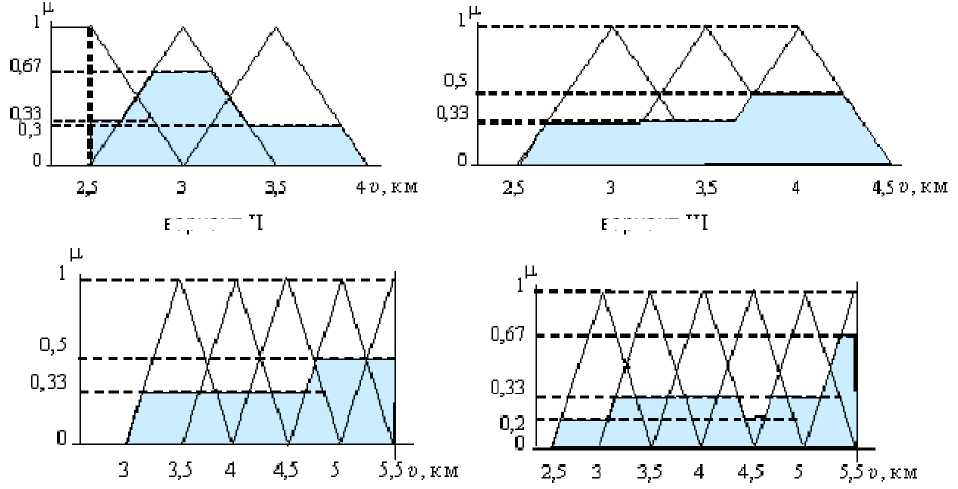
Полученные результаты применения описанной процедуры к остальным рассматриваемым примерам представлены на рис.3.

вариант II вариант III вариант IV вариант V

Рис. 3. Итоговые рисунки для вариантов II, III, IV и V исходных данных

Четвёртый этап. Вычисление точного значения выходной переменной, например, методом «центра тяжести» [4, 6]. Такой метод реализуется в среде MatLab с помощью пакета прикладных программ Fuzzy Logic Toolbox. Однако при этом следует учитывать, что использование этого пакета в полевых условиях уборки урожая может быть затруднено. Поэтому предлагаем более простой метод нахождения значений результирующей переменной. Он состоит в вычислении средневзвешенного значения по итоговому рисунку.

υ ср =_∆ ¹ ∑ h i ∆ i , (11)

где h_i – максимальное значение функций принадлежности, соответствующее изменению скоростей Δ _i ; Δ – полный спектр изменения скоростей.

Результаты расчетов по формуле (11) для всех рассматриваемых примеров представлены в табл.9. Для сравнения там же приведены результаты, полученные с помощью пакета программ Fuzzy Logic Toolbox в среде MatLab.

Таблица 9

Сравнение результатов расчетов (скорости комбайна) по предлагаемой методике и с помощью пакета MatLab

Номер примера	MatLab	Формула (11)	Различие, %
I	3,29	3,2	2,7
II	3,15	3,05	3,2
III	3,6	3,57	0,8
IV	4,43	4,56	2,9
V	4,26	4,24	0,5

Выводы. Предложена методика дефаззификации, которую нетрудно представить в виде алгоритма. Полученные результаты будут использованы в подсистеме обработки нечетких экспертных знаний интеллектуальной информационной системы для технологической регулировки машин. Приближенный способ вычисления точного значения результирующей лингвистической переменной даёт возможность создания компактной программы, которую можно установить на портативном компьютере в полевых условиях, в то время как использование среды MatLab и её приложений затруднительно.

Список литературы О методике дефаззификации при обработке нечеткой экспертной информации

Борисова Л.В. К вопросу построения нечеткой экспертной системы продукционного типа для технологической регулировки машин/Л.В. Борисова, В.П. Димитров, А.К. Тугенгольд//Вестник ДГТУ. -2008. -Т.8. -№3(38). -С.278-287.
Димитров В.П. Оценка параметров лингвистических переменных факторов внешней среды/В.П. Димитров, Л.В. Борисова//Искусственный интеллект в XXI веке. Решения в условиях неопределенности: сб. ст. V Междунар. науч.-техн. конф. -Пенза, 2007. -С.30-32.
Обработка нечеткой информации в системах принятия решений/А.Н. Борисов, А.В. Алексеев, Г.В. Меркурьев [и др.] -М.: Радио и связь, 1989. -394 с.
Прикладные нечеткие системы; пер с яп./К. Асаи, Д. Ватада, С. Сугэно. -М.: Мир, 1993. -368 с.
Пугачев А.Н. Советы комбайнеру/А.Н. Пугачев. -М.: Колос, 1984. -224 с.
Макаров И.М. Искусственный интеллект и интеллектуальные системы управления/И.М. Макаров, В.М. Лохин, С.В. Манько [и др.] -М.: Наука, 2006. -333 с.
Borisova L.V. K voprosu postroeniya nechetkoi ekspertnoi sistemy produkcionnogo tipa dlya tehnologicheskoi regulirovki mashin/L.V. Borisova, V.P. Dimitrov, A.K. Tugengol'd//Vestnik DGTU. -2008. -T.8. -№3(38). -S.278-287. -in Russian.
Dimitrov V.P. Ocenka parametrov lingvisticheskih peremennyh faktorov vneshnei sredy/V.P. Dimitrov, L.V. Borisova//Iskusstvennyi intellekt v XXI veke. Resheniya v usloviyah neopredelennosti: sb. st. V Mejdunar. nauch.-tehn. konf. -Penza, 2007. -S.30-32. -in Russian.
Obrabotka nechetkoi informacii v sistemah prinyatiya reshenii/A.N. Borisov, A.V. Alekseev, G.V. Merkur'ev [i dr.] -M.: Radio i svyaz', 1989. -394 s. -in Russian.
Prikladnye nechetkie sistemy; per s yap./K. Asai, D. Vatada, S. Sugeno. -M.: Mir, 1993. -368 s. -in Russian.
Pugachev A.N. Sovety kombaineru/A.N. Pugachev. -M.: Kolos, 1984. -224 s. -in Russian.
Makarov I.M. Iskusstvennyi intellekt i intellektual'nye sistemy upravleniya/I.M. Makarov, V.M. Lohin, S.V. Man'ko [i dr.] -M.: Nauka, 2006. -333 s. -in Russian.

Еще

Статья научная