О методике представления нечётких экспертных знаний

Экспертная информация, как правило, трудно формализуема в рамках традиционных математических подходов, что обусловило применение в этой области теории нечетких множеств и широкое использование баз знаний, основанных на нечетких знаниях, т. е. нечетких продукционных систем [3

выводы на основе правил нечёткой логики, что делает актуальной задачу адекватного представления нечеткой экспертной информации. Для формирования такой информации (на этапе фаззификации) необходимо определить функции принадлежности (ФП) лингвистических переменных (ЛП) модели предметной области, в том числе установить оптимальное число термов ЛП. При этом возникает вопрос о критериях при оценивании того или иного признака, по которым должен производиться выбор оптимального множества значений лингвистической шкалы.

Постановка задачи. При описании реальных объектов критерий оптимальности выбора термов ЛП должен удовлетворять требованиям минимальной неопределенности для экспертов и максимальной согласованности экспертной информации [5, 6]. С практической точки зрения эта задача сводится к установлению оптимального множества используемой для оценки параметров модели предметной области лингвистической шкалы и оптимального числа термов ЛП. Сверху число термов ограничено соображениями точности измерения рассматриваемого параметра. А нижняя граница должна быть такой, чтобы возможно было выявить и описать взаимодействие входных параметров с выходными. При решении рассматриваемой задачи проводят оценку согласованности нечетких экспертных знаний.

Основные положения. Представление экспертных знаний в конкретной предметной области предполагает определение конечного множества ЛП, термов для каждой ЛП, построение ФП и оценку согласованности экспертной информации. Ключевым моментом при построении ФП является определе-

Работа выполнена по тематическому плану Министерства образования и науки РФ № 1.12.12; № госрегистрации ние базового и расширенных терм-множеств. В общем случае базовое терм-множество ЛП имеет вид [5]:

7? = {7Г, Tj, ... Т}}, (/ё К = {1, 2,..., /77}).

Здесь (Т, ,Х;С) - нечёткая переменная, соответствующая терму TieT;

G - носитель нечёткого множества С,. Термы ЛП в соответствии с физическим смыслом определены на действительной оси R.

Будем рассматривать нормальные нечёткие множества, для которых высота равна 1, т.е. верхняя граница функции принадлежности равна 1 (supp(x) 1). Нечеткие множества могут быть как хеЕ унимодальными, т.е. р^ (%) = 1 только при одном значении % из Е, так и имеющими область толерант ности.

Для выбора оптимальной модели в качестве критерия согласованности целесообразно использовать показатели общей и парной согласованности. При анализе согласованности нечёткой экс пертной информации на первом этапе используют аддитивный и мультипликативный показатели общей согласованности. По их величинам формулируется суждение о согласованности моделей экспертного оценивания. На втором этапе строится матрица парной согласованности моделей X и X экспер тов.

Общая согласованность множества моделей экспертного оценивания признака определяется аддитивным к и мультипликативным к показателями [6, 7]

₀         1,2,...,

₀         1,2,...,

1 min

1       ₀         1,2,...,

1 ¹ max            ^,

0        1,2,..., где / = 1,2,...,т- номер терма, i = 1,2,...,к- номер эксперта, р(х)-ФП, которую задал / — ый эксперт для /-го терма.

Матрица К*_т парной согласованности моделей X и X экспертов строится на основе показателей согласованности к*₅ между моделями двух экспертов, i- го и у-го, в рамках /-го терма [6, 8]:

min ки = 10--------------------------- .                                         (2)

max 0

Km

согласованности моделей X и X по всем термам. Её элементы определяются формулой [6, 9]:

1 _,

9 т 2—* у где т — число термов.

Анализ аддитивных и мультипликативных показателей, а также матриц парной согласованности для моделей с разным количеством термов может быть использован для выбора оптимального количества термов ФП [6].

В качестве альтернативного подхода к оценке согласованности экспертной информации применяется метод минимизации средневзвешенного квадратического отклонения F m параметров от усреднённых значений:

⁴           \  к min                                    tax

^т -                  ^а)) min,                             (4)

/=1 /■=1 j= 1

где а 1   a2il — границы толерантности нечёткого числа р^Сг), а3' и 541 — его левый и правый коэф фициенты нечёткости соответственно, а^ — их усреднённые значения, ооi енты экспертов.

Из необходимого условия экстремума функции Fm получаем к aj =^>ia'].

/= 1

При заданных весовых коэффициентах и постоянном количестве и составе экспертов Fm зависит только от числа термов модели. Оптимальным числом термов будет такое, для которого Fm при мет наименьшее значение.

Сформированная таким образом экспертная информация служит для получения обобщённой ФП, которая используется затем в системе нечёткого логического вывода. При этом результативность и эффективность вывода обеспечивается в значительной степени максимальной согласованностью экспертной информации. Возникает вопрос о выборе весовых коэффициентов, который не является тривиальным. Общепринято в качестве начального приближения для решения прикладных задач использовать равные для всех экспертов весовые коэффициенты, что естественно только при равной квалификации экспертов.

Именно такой подход использован нами в реализованной программной системе ввода и корректировки экспертных знаний [10]. Однако оценки экспертов основаны не только на их квалификации, зачастую разной, но и использовании экспертами косвенных средств объективного контроля разной точности. Очевидна необходимость введения различных весовых коэффициентов экспертов. В настоящей работе предложено использовать для вычисления весовых коэффициентов числа Фишбер-на [И]. Использование правила Фишберна позволит учесть значимость оценок различных экспертов. Введём ранги экспертов г, и установим соотношение /1> г2 ... > гк . Набор весов Фишберна для си стемы строгих предпочтений определяется по формуле

2 (/V - / + 1)

“ /У(/У +1), где N- число экспертов, i — номер эксперта по значимости.

Для смешанной системы предпочтений, когда наряду с предпочтениями в систему входят отношения безразличия, весовые коэффициенты Фишберна имеют вид:

Ь

r_N = 1, / = N ,

/V

2; Ь = Ца, /=1

_\aj , если rv 1 где а^ 1

Уа.ч 1, если г,. 1 >П

Для ранжирования экспертов могут быть использованы различные соображения, например, степень согласованности их информации с оценками остальных экспертов.

Для иллюстрации предлагаемой методики оценки согласованности экспертной информации будем рассматривать предметную область «Комбайновая уборка зерновых культур» [12]. В силу фор- мализма используемого математического аппарата, такой выбор никак не ограничивает общности рассмотрения. Априорный анализ предметной области показал, что для рассмотрения вопроса о выборе оптимального множества лингвистической шкалы, используемой для оценивания факторов внешней среды, регулируемых параметров машины и показателей качества работы, целесообразно проведение анализа согласованности экспертной информации.

Для иллюстрации подхода рассмотрим несколько входных ЛП данной предметной области: ЛП1 «влажность хлебостоя», ЛП2 «соломистость хлебной массы», ЛПЗ «засорённость хлебной мас

--  -

Описание ЛП

Таблица 1

ЛП	Модель	Термы
ЛП1	2-	«сухой», «влажный»
	3-	«сухой», «нормальный», «влажный»
	4-	«сухой», «нормальный», «влажный», «очень влажный»
ЛП2	2-	«низкая», «высокая»
	3-	«низкая», «средняя», «высокая»
	4-	«низкая», «средняя», «высокая», «очень высокая»
ЛПЗ	2-	«низкая», «высокая»
	3-	«низкая», «средняя», «высокая»
	4-	«низкая», «средняя», «высокая», «очень высокая»

Оценки функций принадлежности ЛП представили 4 эксперта. Для описания термов использовались типовые функции трапециевидного типа (табл. 2) [13].

Таблица 2

Вид и параметры функций принадлежности

Вид терма	Выражение для ФП
Левый терм	Г 1,    если     x < a bx xab             a x b ba 0,   ес ли    x > b
Центральные термы	0, ес ли x < a xa ----, ес ли a < x < c ca ц( x,a,b,c,d^ =    1,    еели c bx ----, ес ли d 0, ес ли x > b
Правый терм	Г 0,    еели x < a xa xab             x b ba 1,    еели x > b Область определения для хот 0 до 1 (нормированные значения). Об , , ,

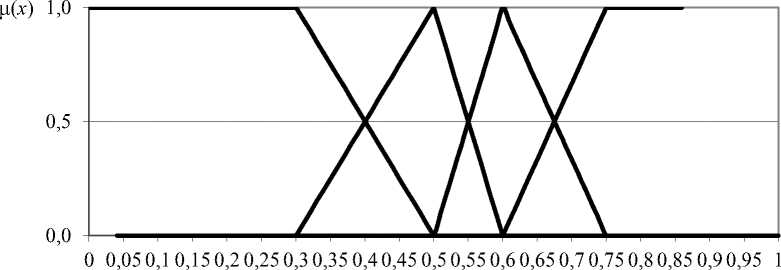
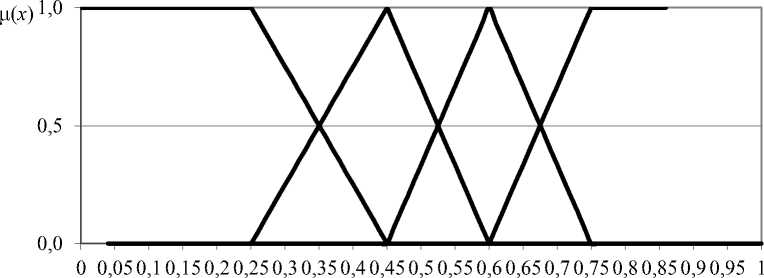
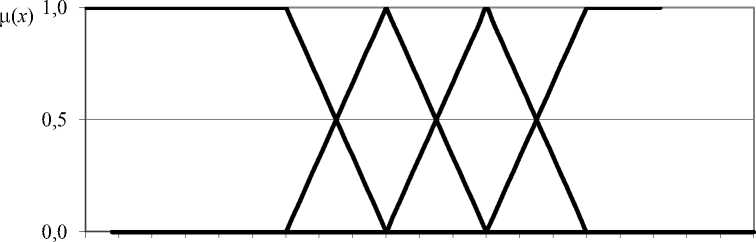
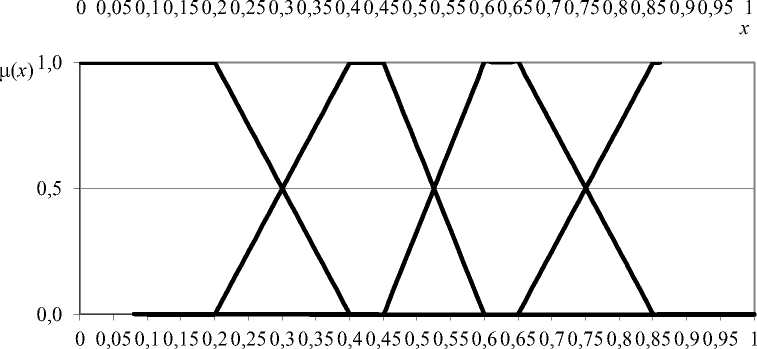
Для расчётов использованы значения коэффициентов ФП, представленные экспертами. В качестве примера на рис. 1 приведены ФП термов ЛП2, установленные экспертами для 4-хтермовой модели.

x

x

Рис.1. Функции принадлежности для ЛП2

Для расчёта аддитивных к и мультипликативных к показателей по формулам (1) и вычисления матриц парной согласованности по формулам (2) и (3) использована программная система приобретения знаний (подсистема экспертной системы) [10]. Результаты расчётов представлены в табл. 3.

Таблица 3

Результаты расчёта показателей кп к

лп	Модель	к	к
ЛП1	2-хтермовая                 \	0,817	0,816
	3-хтермовая	0,784	0,78
	4-хтермовая	0,669	0,657
ЛП2	2-хтермовая	0,809	0,809
	3-хтермовая	0,815	0,812
	4-хтермовая	0,653	0,644
ЛПЗ	2-хтермовая	0,835	0,832
	3-хтермовая	0,757	0,746
	4-итермовая	0,696	0,687

Анализ полученных показателей общей согласованности экспертной информации показывает, что наиболее согласованной для ЛП1 и ЛПЗ является 2-х термовая модель, а для ЛП2 - 3-термовая модель.

Результаты вычислений матриц парной согласованности для всех моделей позволяют вычислить средневзвешенные квадратические отклонения F m параметров, оцениваемых экспертами, от усредненных значений этих параметров. При этом использованы, как равные весовые коэффициенты, так и веса, вычисленные по правилу Фишберна для строгой (6) и смешанной (7) систем предпочтений. В табл. 4 приведён фрагмент результатов расчёта для ЛП2.

Матрицы парной согласованности, ранги экспертов и весовые коэффициенты Фишберна

Таблица 4

Модель	Матрица K'L м    m				Сумма	Ранг эксперта	Числа Фишберна
2-х              \ термовая	1	0,951	0,92	0,843	3,714	2	0,3
	0,951	1	0,905	0,818	3,674	3	0,2
	0,92	0,905	1	0,904	3,729	1	0,4
	0,843	0,818	0,904	1	3,565	4	0,1
3-х              \ термовая	1	0,9	0,903	0,855	3,658	4	0,1
	0,9	1	0,907	0,947	3,754	1	0,4
	0,903	0,907	1	0,861	3,671	2	0,3
	0,855	0,947	0,861	1	3,663	3	0,2
4-х              \ термовая	1	0,841	0,88	0,653	3,374	3	0,2
	0,841	1	0,948	0,772	3,561	1	0,4
	0,88	0,948	1	0,73	3,558	2	0,3
	0,653	0,772	0,73	1	3,155	4	0,1

Ранжирование экспертов проводилось на основе критерия наибольшей парной согласованности, для чего использовались суммы элементов строк матрицы парной согласованности.

Рассчитаны параметры обобщённых ФП и величины F m из условия (5) для всех моделей. Результаты расчётов величины F m представлены в табл. 5.

Таблица 5

Величины m для рассматриваемых ЛП

ЛП	Модель	F m
		равные весовые коэффициенты	весовые коэффициенты Фишберна
ЛП1	2-хтермовая        \	0,0125	0,01065
	3-хтермовая	0,008125	0,00705
	4-хтермовая	0,01125	0,01115
ЛП2	2-хтермовая	0,014688	0,00985
	3-хтермовая	0,005938	0,0055
	4-хтермовая	0,004063	0,0035
ЛПЗ	2-хтермовая	0,004375	0,00358
	3-хтермовая	0,007188	0,0047
	4-итермовая	0,010625	0,0084

В табл. 6 сопоставлены результаты определения оптимального числа термов ЛП, полученные на основе рассмотрения показателей согласованности и методом минимизации средневзвешенного квадратического отклонения F m индивидуальных параметров, задаваемых экспертами, от усредненных значений этих параметров.

Таблица 6

Оптимальные модели для ЛП

ЛП	Оптимальное число термов
	По показателям согласованности	По величинам F m
ЛП1	2	3
ЛП2	3	4
ЛПЗ	2	2

Данные табл. 5 и б позволяют сделать вывод, что для построения обобщённых ФП с целью максимальной согласованности экспертной информации предпочтительнее использовать весовые коэффициенты Фишберна с ранжированием экспертов по степени согласованности их информации с остальными. На рис. 2 представлен график обобщённой ФП для 3-х термовой модели ЛП2 с учетом весовых коэффициентов Фишберна.

Ц( x ) 1,0

0,5

0,0 —I I ^^^^^^^^^^^^^^^^^^^^

0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9 0,95 1

x

Рис. 2. Обобщённая функция принадлежности

Таким образом, в условиях требования наибольшей согласованности экспертных оценок, применение весовых коэффициентов Фишберна даёт наилучший результат. Отметим, что предложенный метод актуален для других вариантов ранжирования экспертной информации, например, по уровню квалификации экспертов.

Заключение. Разработана методика формирования базы знаний экспертной системы, позволяющая устанавливать оптимальные модели представления нечётких знаний, адекватные реальным условиям функционирования техники. Важным критерием пригодности экспертной информации для использования на этапах композиции и дефаззификации является её согласованность. В работе проанализированы подходы к оценке согласованности и введены различные весовые коэффициенты экспертов, а для ранжирования экспертов в качестве критерия применена степень согласованности информации каждого эксперта с остальными. В качестве весовых коэффициентов предлагается использовать числа Фишберна. Методика применена к созданию базы экспертной информации в предметной области «Комбайновая уборка зерновых культур». Рассмотрены значимые входные ЛП, для которых установлены экспертные оценки, построены модели с 2-х, 3-х и 4-х термовыми ФП, вычислены характеристики общей и парной согласованности моделей экспертов, параметры обобщённых ФП в случаях равных весовых коэффициентов и весов Фишберна. Для каждой из ЛП выбрана оптимальная модель и построена обобщённая ФП. Показано, что наибольшая согласованность экспертной информации достигается при использовании весовых коэффициентов Фишберна, важным при этом является факт сохранения информации всех экспертов. Таким образом, использование весовых коэффициентов Фишберна позволяет сформировать экспертную информацию, обладающую наибольшей из возможных степенью согласованности, не утрачивая при этом её ценных составляющих, характеризующих индивидуальный опыт и знания эксперта.