О методике расчета основных параметров универсальных аэрожелобов

Введение . В период массового поступления зерна наибольшую актуальность приобретает обеспечение сохранности качества свежеубранного урожая как на стадиях временного хранения, так и окончательной закладки на длительное хранение. Наиболее целесообразным и экономическим выгодным является использование универсальных трехканальных аэрожелобов, способных в комплексе осуществлять операции сушки, активного вентилирования и пневматической выгрузки зерна. Аэрожелоба представляют собой систему воздухораспределительных коробов различной длины, снабженных перфорированными решетками. Принцип работы аэрожелобов заключается в подведении воздушного потока под напором в воздухораспределительные короба. Во время временного хранения зернового материала в промежутках до направления в сушильное отделение, как обычно, в качестве воздушного потока использовался ночной холодный при активном вентилировании и подогретый в калориферах горячий воздух при сушке. Несмотря на эффективность обработки, использование такого вида энергии сопровождается значительными экономическими затратами. Во многих странах уже имеются целые государственные программы альтернативных источников производства энергии. В работе [1] сделана попытка получения энергии для сушки зерна гелиосушилкой, разработана лабораторная установка, проведены эксперименты и доказана работоспособность установки.

Цель исследований . Выявление условий функционирования и работоспособности универсальных аэрожелобов в режимах сушки и пневматической разгрузки в условиях подачи агента, разогретого солнечными лучами. В работе основное внимание уделено режиму пневморазгрузки, наиболее энергоемкому по сравнению с другими операциями (сушкой, активным вентилированием).

Задача исследований . Изучение методики расчета основных параметров универсальных аэрожелобов, способных осуществлять вышеназванные режимы.

Результаты исследований и их обсуждение . В аэрожелобах при создании условий, когда скорость потока воздуха V в становится выше V кр , зерно приобретает свойство псевдоожиженного состояния и перемещается подобно реальной жидкости [2] вдоль оси транспортирующего канала. Многими исследователями предпринимались попытки математически моделировать характер движения зерна в таком состоянии. Однако очень сложно, а в большинстве случаев невозможно, пользоваться системой дифференциальных уравнений, описывающих движение реальной жидкости, тем более движение зернового потока.

На практике многими исследователями для разработки методики расчетов подобных случаев приходится пользоваться уравнением Бернулли. В нашем случае для определения потерь напора, скоростей, рас- ходов и времени истечения псевдоожиженного зернового слоя также воспользуемся уравнением Бернулли для реальных жидкостей с рядом допущений.

В универсальных аэрожелобах перемещение зерна идет как в открытом сосуде с боковым истечением, в котором высота перемещаемого зернового слоя имеет переменный равноубывающий по времени уровень (рис.). Примем перемещение зерна как ламинарное, без скачков и перепадов, движение, считающееся установившимся.

Уравнение Бернулли имеет силу и для вертикального, и для горизонтального истечения из сосудов [2].

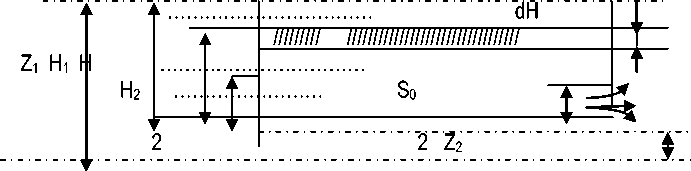
Схема истечения зернового потока под воздействием воздушных струй

Выбрав плоскость сравнения О–О параллельной днищу сосуда, напишем уравнение Бернулли для сечения 1–1, соответствующего верхнему уровню зернового слоя в канале, и сечения 2–2, плоскость которого проходит через самое узкое сечение вытекающей струи:

^i ■''■.,''/■■■'

pg 2д      pg 2д где   Z1 и Z2 – соответственно нивелирная высота (геометрический напор), которая представляет собой удельную потенциальную энергию положения в данной точке (данном сечении);

^ и ^ - статический или пьезометрический напор, характеризует удельную потенциальную энергию давления в данной точке (данном сечении);

2д и 2д — скоростной, или динамический напор, характеризует удельную кинетическую энергию в данной точке (данном сечении).

Согласно уравнению Бернулли, гидродинамический напор не меняется при переходе от поперечного сечения 1–1 к сечению 2–2.

Движение зерна по транспортирующему каналу идет согласно открытому каналу, в связи с чем давление в двух сечениях одинаково, т.е. P1=P2. Давление Р1=Р2=ΔР = ρ∙g∙hтр, или Р1-Р2 / ρ∙g = ΔР/ ρ∙g= hтр.

При подстановке ΔР = ρ∙g∙h тр в уравнение Пуазейля для ламинарного движения Q=πd⁴ ΔР/128 μl , заменяя расход Q произведением средней скорости потока ω на площадь поперечного сечения отверстия πd²/4 , получим:

ω πd²/4= πd⁴ ρ∙g∙h тр /128 μl .

Проведя некоторые вычисления, упрощаем уравнение, при котором:

h тр = 64/Re∙l/d∙ ω²/2g .

Принято считать ω²/2g = h ск скоростным напором, а 64/Re – коэффициентом гидравлического трения, или коэффициентом трения, и обозначают в литературе через λ .

Таким образом: ΔР тр = λ∙ l/d∙ ρ ω²/2 .

Примем, что при постоянно убывающем уровне зернового слоя скорость в поперечном сечении 2–2 больше, чем в сечении 1–1, ω 2 >ω 1 . Поэтому скорость зерна будем определять для сечения 2–2.

Вследствие небольшого расстояния от плоскости отверстия в стенке канала до плоскости самого узкого сечения струи примем:

Z 1 –Z 2 ≈ H.

Отсюда ω 2 ²/2g = H .

Следовательно, ^2 =√2 g ℎ․

Поэтому скорость движения зернового слоя запишется как:

Вследствие того, что площадь поперечного сечения струи S о в отверстии больше площади ее самого узкого сечения S 2 , скорость ω о жидкости в отверстии должна быть меньше, чем ω 2 . Тогда:

"о =  ∙ <^2 =  ∙

а =   ∙ £ .

Этот коэффициент зависит от величины критерия Re и его значения приведены в справочнике [3].

Объемный расход жидкости равен произведению ее скорости ω о в отверстии на площадь сечения S о отверстия:

с=а∙ So √2дн , где Н – расстояние от верхнего уровня жидкости до оси отверстия.

Если в это уравнение внести плотность зерна и эквивалент времени, то получим объемную массу зерна за единицу времени:

м =3600∙ а ∙ So ∙ р ∙√2 дн .

Определим время, за которое уровень слоя в емкости опустится от первоначальной высоты Н 1 до некоторой высоты Н 2 . За бесконечно малый промежуток времени через отверстия вытечет следующий объем жидкости (слоя):

dV = сек ∙ dr =  ∙ ^0 √2дн ∙ dr, где S0 – площадь поперечного сечения отверстия в боковой стенке емкости. За этот же промежуток времени dτ уровень слоя в емкости понизится на бесконечно малую величину dH, и при постоянной площади поперечного сечения S емкости убыль жидкости в нем составит:

dV =- SdH ․

Отрицательный знак в выражении указывает на убыль слоя.

Приравнивая согласно уравнению неразрывности потока эти объемы, получим:

∝ ∙ S_o √2 gHdz =- SdH .

Откуда dr=- —․

J                     a∙ So √

Проинтегрируем это выражение, принимая, что коэффициент расхода α постоянен, т.е. не зависит от скорости истечения:

_rT J       f^2 SdH

I . dr=-∫

()            Ji^i a ∙ $o √2дн’ т=     ∫ ^н^/2dH =     (√ н;-√н;).

а ∙ So √ 2д J} ^i                  а ∙ So √                      ^.

В случае полного опорожнения емкости Н 2 =0 уравнение принимает вид:

т — ²⁵ √ Hi ∙   √   ․

Таким образом, пользуясь на практике рекомендациями Бернулли, определим потери напора, расход, скорость и время опорожнения зернового слоя в транспортирующем канале универсального аэрожелоба, принятого как открытый сосуд.

Выводы

• 1.    Движение зерна в универсальных трехканальных аэрожелобах псевдоожиженное, с некоторыми допущениями, принятое как установившееся и описываемое уравнением Бернулли.

• 2.    По приведенным формулам определяются основные параметры универсального трехканального аэрожелоба.