О многосортности потоков в квазиклеточных сетях

В работах автора [1,2,3,4] рассматривались квазиклеточные сети как фундаментальные дискретные структуры, не имеющими сигнатуры [1,3]. Особенности функционирования квазиклеточных сетей тесно связаны с понятием циркуляции [1,3], т.е. передачи состояния между соседними клетками. Переход бинарного состояния между соседними клетками приведён на рис. 1. Введена широкая классификация квазиклеточных сетей [2,5]. Основным назначением квазиклеточных сетей является моделирование систем, рассмотрение которых сводится к моделированию потоков в сетях [2,4,5]. Речь идёт о распространении каких-либо микрообъектов или частиц веществ в ограниченном пространстве.

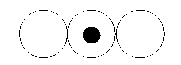
QQ uv

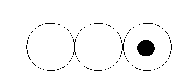
QQ uv

t

t+ θ

Рис. 1. Переход бинарного состояния между клетками.

Структура квазиклеточных сетей синтезируется различными способами, описанными в работах [4,6]. Так, пример квазиклеточной сети, построенной на основе графа приведён на рис. 2.

Несмотря на то, что квазиклеточные сети являются новым типом дискретных структур, они обладают некоторыми сходствами с широко известными графовыми моделями, сетями Петри, моделями потоков в сетях, клеточными автоматами и др.

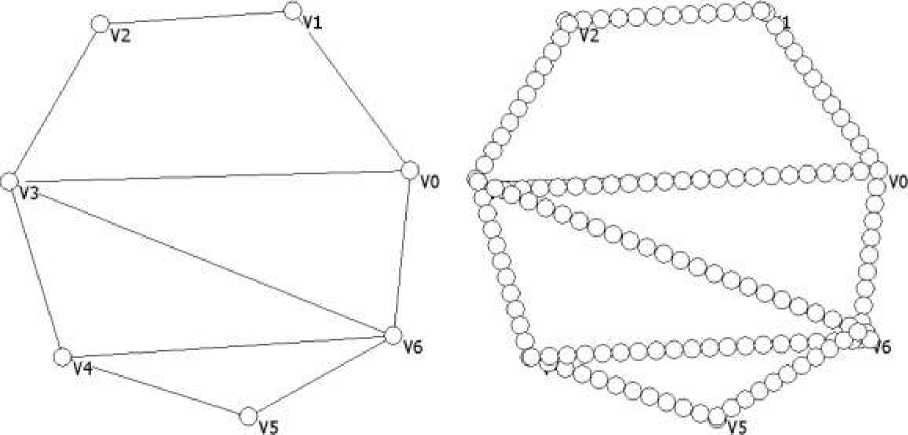
Рис. 2. Базовый граф и построенная на его основе квазиклеточная сеть.

Основным назначением квазиклеточных сетей как дискретных структур является моделирование систем, предполагающих наличие потоков, распространяемых в ограниченных областях пространства. В таких системах достаточно распространённым явлением является разнородность этих потоков. Так, в логистике рассматриваются потоки услуг, финансовые, транспортные, информационные, материальные и др. [7]. В задачах моделирования транспортных систем рассматриваются потоки пассажирского, грузового и транспорта; наземного, подземного и воздушного; дорожного и железнодорожного и т. п. При моделировании бизнес-процессов характерно рассмотрение ресурсов различных типов. Особое внимание в подобных ситуациях следует уделить проблемам взаимодействия и распределения разнородных потоков в системе. Таким образом, многосортные потоки и проблема их моделирования представляет собой достаточно значимую проблему при различных предметных интерпретациях.

Рассмотрим вопросы моделирования многосортных потоков при построении моделей на основе квазиклеточных сетей. В ряде работ [1,4,6] было отмечено, что в квазиклеточной сети каждая клетка задаётся в виде:

Q p =( x_p,y_p,С p ,S_p ) , (1)

где S p - состояние клетки, С p - счётчик потокообразующих состояний (фишек). Пусть имеем участок Q' ( Q ^с Q ), для которого характерно наличие входной и выходной клеток:

^Qвх   ^{( Х}вх , У вх , ^С вх , S вх ) ,

й вых  ^{( Х}вых , ^У вых , ^С вых , S вых )

Тогда величина потока за время t :

^(Q^(t )= C®''(t)- CQ,'(t) .                              (4)

При наличии нескольких входов:

^Qexi   ( x exi , y exi , ^Cexi^,Sexi ) ,

Q euxj   ^{( Х}вых) , y вы] , ^Свых] , ^S вых] )

справедливо

z(Q)(t )= Z C Q4 t )-Y C ^ (t)

i                                j .

В случае многосортности потоков предполагается, что через каждую клетку циркулируют различные потоки:

' p = ^{( Х}р ,У р^ 1, F 2, ... ^,Fi , ... ) F i =( С pi ,S pi )

где ^F 1, ^F 2, ^{... , F}i^{, ...} – векторы параметров потоков, циркулирующих через клетку. Фактически, речь идёт об измерении состояния клетки. При циркуляции в каждой клетке фиксируется потокообразующее состояние (фишка). Таким образом, состояние клетки при циркуляции многосортных потоков фактически обозначает наличие фазовых переменных, определяющих параметры потоков. В простейшем случае рассматривается бинарное потокообразующее состояние (фишка), т. е.:

Q„ =( x_p,y_p,F i, F 2 ...,F i , ... )

/      F , = ( С p,^       .                     (9)

I           S „ e ( 0,1 )

Фактически подобную ситуацию удобно наглядно представить как циркуляцию фишек нескольких цветов. Тогда рассматривая клетку в виде:

Q = ( B_l,C , ,S_l ) ,

вектор состояния содержит несколько двоичных компонент, каждая из которых обозначает наличие фишки (потокообразующего состояния) определённого цвета (сорта):

{ , = ( S 1, S ₂,...,S j ,... ) S j e ( 0,1 )

Таким образом, многосортные потоки сводятся к моделированию потоков по отдельным компонентам вектора состояния. Однако следует отметить, что в зависимости от специфики предметной задачи, сводящейся к моделированию многосортных потоков в квазиклеточных сетях, возможно установление ограничений, связанных с многосортными потоками. Рассмотрим некоторые группы ограничений. При выполнении (11) рассматриваются потоки для каждой компоненты, т. е. Sj(t) , а для указанных величин устанавливаются различные ограничения.

Ограничение вида:

S j ( t )< Z maxj ( t ) , S j ( t )> Z minj ( t ) ,

Z m,nj ( t ) и Z max^ ( t )   -

называются числовыми ограничениями. Величины соответственно нижнее и верхнее ограничения величины компоненты Sj(t) . В частном случае указанные функции являются константами.

Также возможны ограничения вида:

S i ( t )= f ( S j ( t )) ,

S i ( t )< f ( S j ( t )) ,                                       (13)

S i ( t )> f ( S j ( t )) ,

Такие ограничения называются функциональными. Предполагается, что между потоками разного сорта устанавливается некоторая зависимость. Частным случаем функциональных ограничений являются ограничения зависящие не от потоков другого сорта, а от величин С j ⁽ t ) .

Также следует отметить ограничения, предполагающие, что в одной клетке не должны одновременно находиться потоки разного сорта. Такие ограничения назовём исключающими. Частным случаем исключающих ограничений следует считать ограничения тупиковые, приводящие к тому, что в дальнейшем клетка, в которой возникнет определённая ситуация, затрагивающая потоки различного сорта, не будет участвовать в циркуляции.

Для случая бинарных состояний возникновение исключающих потоков определяется значением сложения по модулю 2, т.е. ⁽ S i ⁽ t ⁾⁺ S j ⁽ t )) mod ² .

Таким образом, рассмотрены возможности квазиклеточных сетей для моделирования разнородных потоков, рассмотрение которых сводится к отдельным компонентам, моделирующим потоки определённого типа. Также следует отметить, что особенности моделирования многосортных потоков в значительной степени зависят от предметной интерпретации и соответствующих ограничений, устанавливаемых для их компонент.

Учитывая тот факт, что в различных системах возможно не только наличие нескольких потоков в одних и тех же областях пространства, но и преобразование различных потоков, следует считать целесообразным введение особого элемента квазиклеточной сети, осуществляющего подобное преобразование. Предметным примером преобразования потоков можно считать логистические системы, когда потоки ресурсов преобразуются в потоки полуфабрикатов, а потоки полуфабрикатов в потоки готовой продукции. Очевидно, что для моделирования такой ситуации целесообразно ввести некоторый элемент квазиклеточной сети – трансформатор, предполагающий преобразование потоков. Пусть квазиклеточную сеть, для которой:

Q ==( X p ,y_p,F i, F 2, ... ,F i , ... )

J        F i =( С ^„ З р )       .                      (14)

I           S pi e ( 0,1 )

Считаем, что прохождение потоков через некоторую клетку Qk предполагает преобразование потоков F i в F j , т. е. при

справедливо:

V t : S i ( t )= 1 ;S j ( t )= 0 ;S i ( t + 0)= 0 ;S , ( t + 0)= 1 . (16)

В случае, когда преобразование потоков занимает некоторое время, работа элемента сочетает условие (16) и работу элемента как турникета[6]. Таким образом, клетка одновременно является и турникетом и трансформатором.

Таким образом, рассмотрены фундаментальные аспекты многосортности потоков в квазиклеточных сетях.

Следует также разобрать ряд примеров многосортных потоков. В условиях объектов массового пребывания людей примером можно считать моделирование движения фанатов футбольных команд. Указанная задача тесно связана с проблемой обеспечения безопасности посетителей стадиона. Если принять наличие фанатов команд соответственно за бинарные величины ^S 1 и S 2 , то каждая клетка примет вид:

Q i =( x„y„z„S , ( t ) ,S 2 ( t )) . (17)

Тогда условие столкновения фанатов команд:

S 1 ( t )= S 2 ( t )= 1 . (18)

Условие (18) фактически обозначает ситуацию, связанную со столкновением фанатов разных команд на стадионе, а значит ситуацию, которую следует исключить. Тогда, при проектировании стадионов и выборе мест установки заграждений следует промоделировать ситуацию и в результате модельного эксперимента установить отсутствие (18).

Ещё одним вариантом взаимодействия многосортных потоков можно считать распространение огня, ядовитых веществ, радиации и т. п. в пространстве объектов массового пребывания людей. В такой ситуации проверяется условие появления потоков людей и потоков отравляющих веществ, огня и т. д. в одной области пространства (клетки). Тогда при выполнении условия (18) появляются пострадавшие, т. е. фактически увеличивается некоторая величина (счётчик количества пострадавших).

Ещё одним примером, тесно связанным с потоками людей является взаимодействие пешеходных и транспортных потоков на переходах через проезжую часть. В такой ситуации условие (18) фактически обозначает наезд на пешехода.

Выше также рассмотрены примеры интерпретации многосортных потоков в квазиклеточных сетях в логистических системах. Указанные примеры являются интуитивно понятными, однако в них обычно не возникает проблемы проверки условия (18).

Таким образом, рассмотрены фундаментальные аспекты многосортности потоков в квазиклеточных сетях и приведены примеры её предметных интерпретаций. Следует отметить, что в условиях квазиклеточных сетей многосортность потоков и их преобразование создаёт условия для моделирования различных промышленнологистических систем, а также транспортных, пешеходных и других потоков. Кроме того, многосортность потоков в квазиклеточных сетях позволяет формализовать различные ситуации, связанные     с распространением этих потоков.

квазиклеточные  сети,  дискретные многопоточность, многосортность quasi   cellular  networks,   discrete multithreading, polysort

структуры,  сети,  потоки, structures,   networks,   flows,