О модели термомеханического поведения кварцевых стекол и конструкций из них

Основным материалом для изготовления различных типов оптических волокон является чистое кварцевое стекло и кварцевое стекло с добавлением легирующих элементов. Легирование малыми (0-10 %) добавками таких оксидов, как GeO 2 , B 2 O₃, P 2 O₅, существенно влияет на свойства кварцевого стекла: коэффициент линейного температурного расширения и зависимость вязкости от температуры (в частности, на температуру размягчения и стеклования).

Наиболее активно используется легированное кварцевое стекло в направлении специальных PM (polarization-maintaining) оптических волокон, в которых за счет конструктивно заложенной анизотропии степени легирования и соответственно свойств материала при охлаждении от температур выше температуры размягчения формируются поля остаточных напряжений. В свою очередь, напряженное состояние влияет на оптические характеристики материала, такие как показатель преломления, в частности двулучепреломление. На этом эффекте и основана работа PM оптических волокон, в которых конструктивные элементы подобраны и расположены таким образом, чтобы в светопроводящей жиле эффект двулучепреломления был максимальным. Существует большое количество вариантов исполнения оптических

PM волокон - bow-tie, elliptical, pseudo-rectangle, elliptical core bow-tie, panda, отличающихся между собой формой и расположением областей легированного стекла. Эти области называются SAP (stress applying part). В PM волокнах типа Panda использована SAP цилиндрической формы с изменяющейся по радиусу по определенному закону степенью легирования.

Одной из важных задач анализа напряженного состояния в конструкциях из легированных кварцевых стекол в применении к производству заготовок оптических волокон различного типа является задача определения остаточных напряжений при охлаждении от температур выше температуры размягчения до комнатной температуры. Так, например, в [1, 2] такая задача решена в термоупругой постановке. Также представляет интерес механическое поведение заготовки при последующем нагреве, в частности прогнозирование эволюции ее внешнего радиуса (габаритного размера).

В условиях когда степень легирования кварцевого стекла сильно неоднородна по объему, необходимо учитывать ее значительное влияние на свойства материала. Поэтому для анализа напряженного состояния в заготовках SAP для PMF типа Panda, степень легирования в которых задана определенной зависимостью от радиуса, мы выбрали аналогичный [1, 2] подход, в дополнение к которому нами использована модель термомеханического поведения, способная адекватно учитывать вклад в формирование полей остаточных напряжений релаксационных процессов и переходов (стеклования), возникающих при охлаждении заготовки.

Модель термомеханического поведения кварцевого стекла в условиях релаксационного перехода

В настоящее время физико-механические свойства и константы чистого кварцевого стекла достаточно хорошо изучены и доступы в литературе [3-5].

Модуль упругости растет от 6500 кг/мм² при комнатной температуре до значений на 9-11% больших при T = 200 ° C, при этом коэффициент Пуассона линейно изменяется от 0,17 до 0,2. Коэффициент температурного расширения чистого кварца мал (5 - 10^-7 К 1 ) и примерно постоянен в области температур стеклообразного состояния. Напротив, зависимость вязкости от температуры существенна.

Наибольшее влияние на эволюцию напряженно-деформированн-ного состояния в кварцевых стеклах, как показывает предварительный расчет, оказывает температурная зависимость вязкости р (рис. 1). В работе [6] для её аппроксимации предложено уравнение Фогеля-Таммана-Фульгера lg(p(T)) = A + -B- ,                    (1)

T To где A = -2,487, B = 15004, To = 253 K.

Однако удобнее использовать соотношения Аррениуса вида

К.

lg( p ( T )) = K 1 + T -,                        (2)

где K 1 =- 5,4154, K ₂ = 2,2316 - 10⁴.

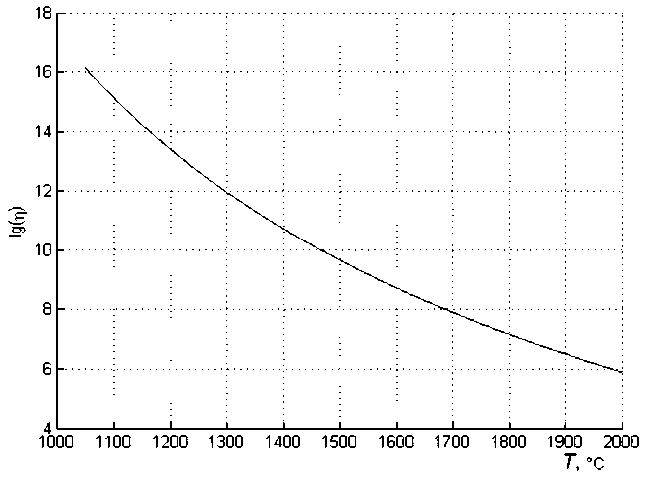
Рис 1. Температурная зависимость вязкости чистого кварца

Учитывая, что на протяжении всей технологической цепочки в заготовках и готовом кварцевом волокне происходят в основном температурные деформации, которые в связи с малостью коэффициента линейного температурного расширения (ЛКТР) а ~ 10 ^{- 7} невелики, была принята гипотеза малых деформаций.

В одноосном случае несвязанная квазистатическая краевая задача о напряженно-деформированном состоянии с учетом малости деформаций и несущественностью вклада массовых сил включает:

уравнение равновесия

— - о, x е l, 5x геометрические соотношения Коши:

5 и

£ -     , x е l.                               (4)

5x где и (x, t) - перемещение вдоль оси х, £( x, t) - полная деформация, а также граничные условия в перемещениях и напряжениях.

В работе [7] в качестве определяющих соотношений использованы соотношения максвеловского типа

S£r о

^О- E ( ^£-^£ т -^£ в ), — B ^- —— .              (5)

5 t   р ( T )

Для вывода определяющих соотношений воспользуемся схемой, предложенной в [6] с использованием функции распределения. Переход из вязкотекучего в стеклообразное состояние в данном случае описывается функцией распределения N (T), которая представляет собой относительную долю объемного содержания застеклованного материала в общем количестве материала. Тогда, предполагая, что для застеклованного материала справедлив упругий закон Гука, а для размягченного стекла - линейно вязкие соотношения, и используя смесе- вые соотношения, получим

о - E • N ( T )( £ -£ т ) + Д ( Т )(1 - N ( T )) — . 5 t

Отметим, что при использовании данных соотношений необходимо знать интервал температур стеклования. Поскольку процесс стеклования описывается функцией распределения, вязкость удобно задавать кусочно-непрерывной функцией типа lg(n(T)) -

K + K 2 , 1 _T

K 1 ⁺

K 2

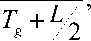
^T >  T g ⁺ LA ■

Для подтверждения на качественном уровне адекватности построенных физических соотношений (6) при релаксационных переходах был численно смоделирован одноосный термомеханический эксперимент на кварцевом стержне, закрепленном с обоих концов:

и ( 0, t ) = u ( l , t ) = 0.                              (8)

Для соотношений (6) был использован закон распределения Лапласа:

NL ( T - T. ^ 1 0,5exp      g , T < Tg V уL V = 1 ( T - T, > 0,5exp---g , T>T I             УL ) где уL - показатель длины промежутка стеклования, Tg - температура стеклования.

На первом этапе (рис. 2) образец охлаждается с постоянной скоростью от температуры, превышающей T g . На втором этапе производится разгрузка стержня. На третьем этапе ненапряженный стержень, защемленный с обоих концов, равномерно с постоянной скоростью нагревается. Напряжение возрастает за счет температурного расширения до тех пор, пока температура не превысит температуру размягчения материала. При дальнейшем нагреве происходит резкий спад напряжений, что объясняется уменьшением характерных времен релаксации до величин, сопоставимых со временем проведения эксперимента за счет уменьшения вязкости.

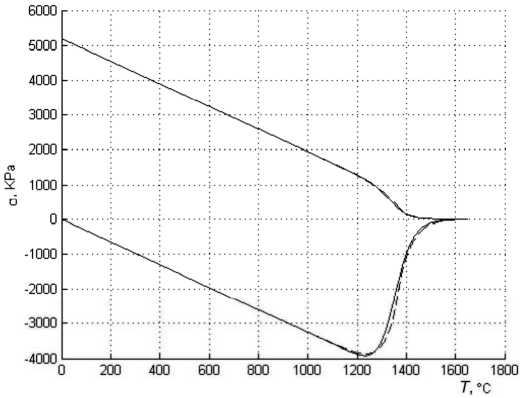
Рис. 2. Термомеханическая кривая защемленного кварцевого образца при скорости охлаждения и нагрева T* = 10 ° С/мин: - с использованием соотношений (4), -- с использованием соотношений (5)

При варьировании скорости охлаждения и нагрева было замечено, что температура стеклования меняет свои значения. Для скоростей T = 1 - 20 ° С/мин получено семейство кривых (рис. 3). Обратим внимание на тот факт, что эти кривые квазипараллельны, и воспользуемся им для построения зависимости температуры размягчения от скорости охлаждения (рис. 4). Заметим, что при увеличении скорости охлаждения рост температуры стеклования замедляется.

Численное решение задачи термомеханики (3), (4), (6)-(8) будем производить пошаговым методом.

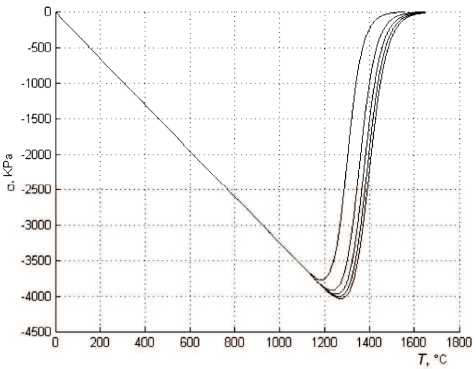
Рис. 3. Семейство термомеханических кривых защемленного кварцевого образца при скоростях охлаждения T = 1 — 20 ° С/мин

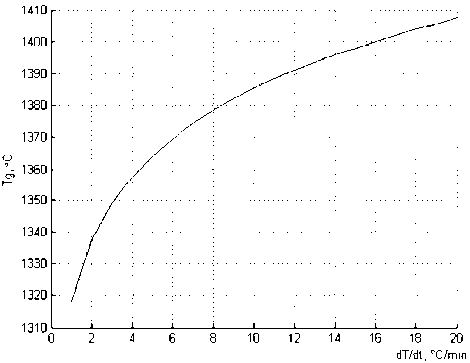
Рис. 4. Зависимость температуры размягчения от скорости охлаждения T

С этой целью введем в рассмотрение сетку на оси времени с узлами: t0 = 0, t1, t2,..., tm, tm+1,.... Тогда можно построить дискретный по времени разностный аналог краевой задачи (3), (4), (6)-(8), который при осуществлении m-го шага по времени будет иметь вид m  mmm

Q = E ( 8 — 8 т — 8 в ),

8m-8m _ Q m tm - tm-1 Л( Tm )

8m =аАTm, что соответствует неявной схеме отыскания неизвестных на m-м временном слое. Теоретический анализ сходимости процесса не производился. Практические вычисления по описанному алгоритму подтверждают сходимость схемы при уменьшении временного шага.

Таким образом, использование определяющих соотношений (5) и (6) приводит к качественно и количественно идентичным результатам. Следовательно, описание термомеханического поведения кварцевых стекол в условиях релаксационного перехода возможно на основе определяющих соотношений, предлагаемых в работе [6] для описания термомеханического поведения стеклующихся полимерных материалов.

Постановка и численное решение задачи термомеханики стеклующегося цилиндра

Рассматривается задача описания эволюции напряженного состояния в осесимметричном длинном цилиндрическом стержне из неоднородного по радиусу материала в процессе охлаждения и последующего нагрева, сопровождающемся релаксационным переходом из размягченного в застеклованное состояние (стеклованием и размягчением).

Для прогнозирования эволюции напряженного состояния необходима математическая модель термомеханических процессов, происходящих при охлаждении конструкции из легированных кварцевых стекол от температур выше температуры стеклования до температуры окружающей среды, способная адекватно отразить поведение материала как в застеклованном или размягченном состояниях, так в условиях переходного релаксационного процесса. Ключевой в этом вопро- се является задача построения определяющих соотношений, отражающих связь тензоров напряжений и деформации в широком диапазоне изменения температур. В данном случае использован аналог модели (5), записанный для сложного напряженного состояния.

Учитывая, что на протяжении всей технологической цепочки в изделии происходят в основном температурные деформации, которые в связи с малостью коэффициента линейного температурного расширения (ЛКТР) а ® 10 7 K 1 невелики, была принята гипотеза малых деформаций. Известно [5], что релаксационные переходы (стеклование или размягчение) не сопровождаются выделением или поглощением тепла. Принимая во внимание отсутствие источников тепла в материале, малость деформаций и пренебрежимо малое диссипативное тепловыделение, можно разделить краевую задачу нестационарной теплопроводности и краевую задачу термомеханики о напряженно-деформированном состоянии, которые в такой постановке являются несвязанными. Будем предполагать, что в стержне реализуются условия существования обобщенного плоскодеформированного состояния при наличии осевой симметрии в распределении свойств материала и температурных полей. Тогда в цилиндрической системе координат постановка задачи нестационарной теплопроводности будет иметь следующий вид [8]: уравнение теплопроводности бT(r, t) 1 б (         бT(r, t))

c(r, T м r, T)—-—=-^1 rX( r, T)—;— I, r ч0, bJ,   (12)

б t     r б r V            б r )

где c ( r , T ) , X ( r , T ) , p ( r , T ) - соответственно теплоемкость, теплопроводность и плотность неоднородно легированного материала, b - радиус стержня;

граничные условия б T (r, t)

^б r    r = 0

= 0,

-Х ( b , T ) ^ T^ б r

r = b

= h ( T ( b , t ) - T ) + 8O 0 T ( b , t ) ⁴ ,

где первое слагаемое правой части описывает конвективный теплопе-ренос, а второе - излучение (закон Стефана-Больцмана), 8 - коэффициент черноты, ст ₀ - постоянная Стефана-Больцмана, h - коэффициент теплоотдачи, T _c - температура окружающей среды;

начальные условия

T ( r ,0 ) = T _o , r g [ 0, b ] .

Несвязанная квазистатическая краевая задача механики с учетом малости деформаций и несущественностью вклада массовых сил включает [9]: уравнение равновесия

• B. rArt) + ОМ-О р<^ = 0, r _е o, b ) ;

  
  

8 r             r геометрические соотношения

• 8 , ( r , t ) = ™- , 8 , ( r , t ) = u ²^, 8 r                   r

8 z ( t ) = const, r g [ 0, b ] ;

граничные условия о r (b, t) = 0,    ur (0, t) = 0,

b jr о z ( r, t) dr = 0,

r G [ 0, b ] .

Система уравнений задачи о напряженно-деформированном состоянии включает также определяющие соотношения [9]. Для описания на единой основе механического поведения кварцевого стекла в температурном диапазоне, включающем релаксационный переход, были использованы определяющие соотношения вида (6)-(7), обобщенные на случай сложного напряженного состояния:

4„z

° r ^{( r} , t ) = ⁽ B ⁺ 3 G ) ( ⁸ r ⁽ r , t ) ^{- 8} Br ^{( r} , t ) - ⁸ T ^{( r} , t ) ) ⁺

+ (B - 3 G) к ( r, t) 8 B9 (r, t ) - 8 T (r, t) + 8 z (t) 8 Bz (r, t) - E T (r, t)] ,

°< p ⁽ r , t ) = ^{( B + 4 G} ) ( ⁸ 9 ⁽ r , t ) ^{- 8} B ф ⁽ r , t ) ^{- 8} T ⁽ r , t ) ) ⁺

³                                                  (18)

• ^{+ ( B} - 3 G ) [ e r ^{( r} , t ) ^-8 Br ^{( r} , t ) ^-8 T ^{( r} , t ) ^{+ 8} z ⁽ t ) ^-8 Bz ^{( r} , t ) ^-8 T ^{( r} , t ) ] ,

о z ⁽ r , t ) = ⁽ B ⁺ 3 G ) ( 8 z ⁽ t ) ^- 8 Bz ⁽ r , t ) -8 T ⁽ r , t ) ) ⁺

+ (B - 3 G) ^8r (r, t) - 8Br (r, t) - 8T (r, t) + 89 (r, t) - 8B9 (r, t) - 8T (r, t)] ,

⁸ B ф ( ^r , t ) = ^{1( а} ф ^-аХ ⁿ

• ⁸ Br ⁽ r , t ) = ¹⁽ ^ r ^X         r ^e ( °- b ) ,               ⁽¹⁹⁾

n

⁸ Bz ⁽ r , t ) = ^{( a} z ^{-a )}

I n

T где 8T (r, t) = ja(r, T)dT - линейная температурная деформация; B -To модуль объемного сжатия; G - модуль сдвига; 8Bф( r, th 8 Br( r, t), 8 Bz (r, t)  - компоненты тензора вязких деформаций 8 B (r, t),

K ( r )

a(r,t) = (ar + аф + аz)/3 - среднее напряжение; n(r,T) = n0 (r)eT(r,t), a(r, T) - вязкость и коэффициент температурного расширения мате риала, зависящие от температуры и от неоднородно распределенных по объему тела легирующих примесей; T0 - начальная температура, при которой предполагается отсутствие в теле напряжений, деформаций и их производных по времени; 8 = 08/6t. Компоненты девиатора тензора вязкой деформации в силу того, что в расплавленном состоянии материал предполагается несжимаемой жидкостью (8rB +8фB +8zB = 0), равны соответствующим компонентам тензора вязких деформаций (левые части (19)).

Для численного решения задачи теплопроводности использован метод конечных элементов в традиционной реализации [10]. Для решения задачи термомеханики (13)-(19) избран пошаговый метод. С этой целью вводится в рассмотрение сетка на оси времени с узлами: 1 ₀ = 0, t 1 , 1 ₂,..., t m , t m _{+ 1},.... Тогда можно построить дискретный по времени разностный аналог краевой задачи (4)-(10), соответствующий неявной схеме отыскания неизвестных на m -м временном слое с итерационным уточнением на каждом шаге величин вязких деформаций по соотношениям (8):

Sa rm ⁽ k )

S r

( r ) ₊ a / ” ⁽ k ) ( r ) -а _ф m ⁽ k ) ( r )

r

= 0, r e ( 0, b ) ;

8 ^- ) ( r , t ) = , _E, -(k ) ( r,t ) = ^U*1M , о r                      r

8 rn⁽ k ) = const, r _e [ 0, b ] ;

o r^{- ( k} ) ( b , t) = 0,     U r^{- ( k )} (0, t) = 0,

J r o z^{- ( k} ) ( r , t ) dr = 0, r g [ 0, b ] . 0

o r^{- ( k} ) ( r ) = ( B ₊ 3 G ) ( _s r^{- ( k} ) ( r ) - 8 Br^{- ( k} ) ( r ) - 8 ”^{( k} ) ( r ) ) ₊

+(B - 3 G) |\-(k) (r) - 8Bф-(k) (r) - 8T-(k) (r) + 8z-(k) - 8Bz-(k) (r) - 8/(k) (r)] , o-(k) (r) = (B + 3 G) (8ф-(k) (r) - 8Bф-(k) (r) - 8T-(k) (r)) +

+ (B - 3 G) [8r-(k) (r) - 8Br-(k) (r) - 8T-(k) (r) + 8z-(k> - 8Bz-(k> (r) - 8t-(k> (r)], oz-(k) (r) _ (B + 3G)(8z-(k) - 8Bz-(k) (r) - 8T-(k^(r)) +

₊ ( B - 3 G ) [8 r^{- ( k} ) ( r ) - 8 Br^{- ( k} ) ( r ) - 8 T^{- ( k} ) ( r ) ₊ 8 ф ^{- (} k > ( r ) - 8 b ф ^{- (} k > ( r ) - 8 t^{- (} k ) ( r ) ] ,

8 Bi^{m ( k} ) ( r ) -8 Bi ^{- - 1( k} ) ( r ) _ l( o ? ^{( k - 1)} -o ^{- ( k - 1)} )( t ^- - 1 ^{- - 1} ) , i _ r , ф , z ; r _e( 0, R ) , (24) H

K ( r ) ,^T- ( r )

T

m

⁸ t ^{- ( r} ) ^_ J ^a ( ^T ) ^dT ; h ^{( r} , ^T - ) ^_4) ( ^r ) e

T 0

где k = 1,2,3,... - номер итерации при отыскании неизвестных на - -м слое. В качестве начальных значений неизвестных для итерационного процесса на - -м слое выбираются найденные значения на предыдущем ( - - 1)-м временном слое. Начальные по времени условия для всех величин определяются из условия естественного начального ненапряженного и недеформированного состояния.

Теоретический анализ сходимости итерационного процесса не производился. Практические вычисления по описанному алгоритму подтверждают сходимость итераций.

Вычисления на каждой итерации - -го шага по времени в расчетной схеме (20)-(25) сводятся, по сути, к решению краевой задачи линейной термоупругости. Для численной реализации использован метод конечных элементов.

Численный анализ эволюции напряжений

Описанная математическая модель применена для анализа эволюции напряженного состояния при изготовлении силовых стержней, являющихся частью конструкции заготовки анизотропного оптического волокна, их назначение - формирование в светопроводящей жиле анизотропии поля остаточных напряжений для обеспечения разности показателей преломления материала в ортогональных направлениях. Силовые элементы изготавливаются из кварцевого стекла, легированного малыми добавками (до 10 %) оксида бора и/или фосфора, которые на порядок увеличивают ЛКТР стекла и изменяют диапазон температур стеклования в сторону более низких значений.

В PM волокне типа Panda в качестве SAP используются цилиндрические стержни с переменной зависимостью от радиуса концентрацией легирующих элементов. В начале процесса изготовления силовых стержней осуществляется высокотемпературное химическое осаждение легирующих элементов из паровой фазы на внутреннюю поверхность кварцевых труб (метод MCVD), после чего трубка «схлопывается», т.е. превращается в монолитный стеклянный цилиндр путем разогрева до 1800 ° С в пламени газовой горелки. В дальнейшем заготовка охлаждается на воздухе до температуры окружающей среды. С охлажденного силового стержня плавиковой кислотой стравливаются наружные (нелегированные) слои. При проектировании силового стержня необходимо выбрать зависимость концентрации легирующих добавок от радиуса, обеспечивающую максимальную температурную деформацию стержня при соблюдении условий сохранения прочности на протяжении всего процесса охлаждения заготовки. В работе рассмотрены зависимости концентрации легирующих элементов от радиуса при фиксированном максимальном значении 10 %.

При расчетах по схеме (1.20)-(1.25) принята зависимость динамической вязкости от температуры Т и коэффициента концентрации легирующего элемента ц вида lg( p ( T , ц )) = к 1 ( ц ) + ^2^ . Зависимости для вычисления а (Т , ц ), к 1 ( ц ), к ₂ ( ц ) получены численно в виде кусочной сплайн-интерполяции в результате обработки данных эксперимента [8].

Силовой стержень представлен цилиндром бесконечной длины с радиусом b , который до r = r ₀ <  b имеет переменную по радиусу степень легирования кварца оксидом бора В 2 О 3 . Для моделирования распределения концентрации легирующих добавок по радиусу использованы варианты зависимостей вида

Ц ( r ) =Ц тах

V

n

r

V ^r 0 J J

r е [ °, ^Г 0 ]

где p _max - максимальная концентрация легирующей добавки в центре силового элемента.

При решении задачи теплопроводности (12)-(14) принималось допущение, что коэффициент теплопроводности, теплоемкость и плотность в исследуемом диапазоне концентраций (до 10 %) слабо зависят от массового содержания легирующей добавки, что соответствует экспериментально установленным фактам [11]. Их температурная зависимость выбиралась аналогичной зависимости для чистого кварца.

Для аналитического описания температурных зависимостей использовалась сплайн-интерполяция, построенная на экспериментальных значениях. Плотность полагалась постоянной и равной 2200 кг/м3 [11].

Анализ напряженного состояния в силовых элементах

В результате численного анализа температурного поля в процессе охлаждения заготовки силового стержня сделан вывод о том, что неравномерность распределения температуры по радиусу силового стержня незначительна и не превышает 10 оК. Следовательно, основное влияние на поле остаточных напряжений оказывает концентрация легирующего элемента.

Величины технологических напряжений в SAP при охлаждении после схлопывания исходной заготовки значительно ниже остаточных и опасности не представляют. На рис. 5 приведены законы изменения во времени интенсивности напряжений о i и первого главного напряжения о 1 в трех характерных точках сечения: r = 0 - центр сечения, r = r₀ = 3 - 10³ м - граница легированной зоны и чистого кварца, r = b = 5 - 10³ м - наружная граница.

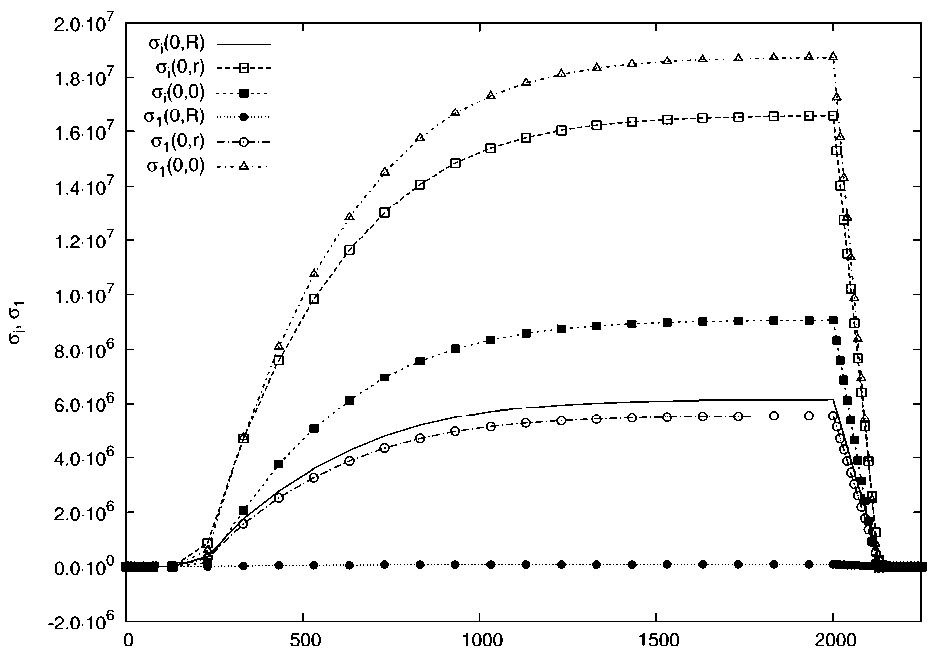
time (s)

Рис. 5. Эволюция интенсивности напряжений _о i и ^ 1 в трех характерных точках сечения силового стержня во время основных этапов изготовления оптического волокна типа Panda

Как видно из приведенных эпюр, наиболее опасным является нормальное растягивающее напряжение а 1 (вдоль оси стержня) в центре стержня и интенсивность напряжений на границе ( r = r ₀ = 3 • IO ^{- 3} м).

Заключение

Таким образом, дано описание двух подходов к построению определяющих соотношений термомеханического поведения кварцевых стекол в условиях стеклования и размягчения. Установлено, что оба подхода прогнозируют практически идентичные законы эволюции напряжений в кварцевом стержне в условиях стеклования. Показано применение одной из моделей для описания формирования полей напряжений и деформаций в сплошном круговом неоднородном кварцевом цилиндре (заготовке силового стержня анизотропного оптического волокна) в условиях охлаждения и нагрева.