О моделировании поверхностного роста твердых тел под действием напряжений
Автор: Измайлова Я.О., Фрейдин А.Б.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
С поверхностным ростом твердых тел связаны различные процессы, такие как биологический рост, формирование покрытий, процессы, сопутствующие аддитивным технологиям. Эксперименты показывают, что процессом роста живой и неживой материи можно управлять с помощью внешних воздействий, в том числе механических. В данной работе представлена модель поверхностного роста, основанная на использовании выражения конфигурационной силы, полученного из фундаментальных балансов массы, импульса и энергии и второго закона термодинамики в виде неравенства Клаузиуса - Дюгема. Показано, что конфигурационной силой является нормальная компонента тензора, названного тензором поверхностного роста, которая управляет процессами роста и адаптации к внешним механическим нагрузкам. Сформулировано кинетическое уравнение в виде зависимости скорости роста от тензора роста. Рассмотрено твердое тело, в котором происходит объемный подвод и последующая диффузия вещества к границе тела. На поверхности тела наблюдается превращение одного вещества в другое, вследствие чего происходит поверхностный рост тела или резорбция. Процесс поверхностного роста зависит от напряженно-деформированного состояния тела и концентрации диффундирующих веществ. В процессе роста напряжения и деформации изменяются, влияя на конфигурационную силу и на подвод вещества, который также влияет на конфигурационную силу. Кроме того, модель учитывает ростовые деформации, возникающие в новых слоях материала и также влияющие на скорость роста тела. Таким образом, имеется связанная задача, включающая описание процессов подвода, диффузии, роста и определение напряженно-деформированного состояния. В качестве апробации модели решены задачи поверхностного роста различных тел при разных условиях нагружения.
Рост, тензор поверхностного роста, кинетика, адаптация тканей, ростовые деформации
Короткий адрес: https://sciup.org/146282030
IDR: 146282030 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.4.09
Текст научной статьи О моделировании поверхностного роста твердых тел под действием напряжений
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN
Поверхностный рост тел включает в себя широкий спектр различных процессов, основанных на изменении массы, объема или геометрии тела вследствие добавления или отсоединения материала на поверхности рассматриваемого тела. Значимость изучения поверхностного роста обусловлена возможностью применения математической модели процесса в разнообразных сферах. Среди них – аддитивные технологии, геологические процессы, такие как образование горных пород и ледяного покрова, аккреция и рост планет, рост деревьев и растений, рост и адаптация твердых и мягких тканей. Кроме того, для биологических тканей процессы адаптации зачастую связаны с различными возможными заболеваниями, носящими масштабный характер у людей старшего возраста. Исследование процесса роста и способов влияния на него позволит контролировать течение подобных заболеваний.
Проблема поверхностного роста изучается уже много десятилетий, и к настоящему времени накоплено большое количество как экспериментальных данных, свидетельствующих о значительном влиянии механических воздействий на поверхностный рост, так и различных математических моделей. Исследование роста для аддитивных технологий, построение аналитической модели, включающей анализ возникающих остаточных напряжений, представлено в [1]. Кроме того, влияние остаточных напряжений исследовалось в [2]. Стоит отметить, что остаточные напряжения, а также дополнительные ростовые напряжения и деформации являются отличительной особенностью ростовых процессов. В зависимости от рассматриваемого феномена они могут иметь разную природу и по-разному влиять на рост тела. Поэтому данный вопрос изучается во многих работах, посвященных поверхностному росту. Геометрическая несовместность, приводящая к появлению остаточных напряжений и неустойчивости, рассматривается в работах Л. Трускиновского с соавторами [3, 4]. Кроме того, в данных работах показано, что несовместность и неустойчивость можно использовать для обеспечения определенного поведения рассматриваемых систем. Помимо этого, некоторые задачи роста тел, решаемые на основе методов дифференциальной геометрии, рассматриваются в работах [5, 6]. Модели, основанные на геометрических методах, применяемых в механике несовместных деформаций, возникающих в процессе роста, можно найти в работе [7]. Также механика растущих тел, в том числе в задачах биологического роста, широко освещается в работах [8, 9]. Теория роста, основанная на термодинамике необратимых процессов, где напряжения Эшелби представляют собой движущую силу необратимого процесса роста, представлена в работах M. Epstein и G. Maugin [10, 11]. Математическое описание кинематики роста приведено в работе [12]. Также стоит отметить, что задачи, аналогичные рассмотрен- ным в представленной работе, а именно рост и аккреция цилиндрических и сферических тел в присутствии преднапряженных слоев, рассмотрены в [13]. В данной работе подробно описаны кинематика и возникающие остаточные напряжения, однако не уделено внимание термодинамике процессов роста.
Как уже было сказано, проблемы роста охватывают широкую область задач в различных научных сферах. Достаточно большое количество работ посвящено биологическому росту. В зависимости от ткани или органа рост протекает по-разному, учитывая особенности строения, гормональной регуляции и функций объекта. В работах A. Goriely с соавторами [14, 15] представлена обобщенная математическая теория для проблем биологического роста и приведено большое количество примеров. Подходы, основанные на движущей силе, управляющей процессами роста, были представлены J.-F. Ganghoffer и I. Goda и соавторами в [16–18]. В этих исследованиях были разработаны модели роста в рамках термодинамики необратимых процессов. Движущей силой процесса перестройки и роста тканей являются напряжения Эшелби. Кроме того, в данных работах представлено конечно-элементное моделирование некоторых задач. Важные работы, связанные с исследованиями роста мозга и развитием эмбриона, представлены E. Kuhl с соавторами [19, 20]. В них описаны как математическая модель, основанная на механике сплошных сред, так и численные симуляции роста мозга, опухолей и некоторых других тканей и органов, предсказывающие реалистичную морфологию, а также даны экспериментальные данные. Также имеются работы, посвященные росту деревьев и растений, который моделируется на основе различных принципов. Так, в [21] рассматриваются остаточные напряжения, которые играют наиболее важную роль в процессах роста, и в случае деревообрабатывающей промышленности ведут к образованию значимых дефектов. В [22] представлена модель роста корней, где корень моделируется как двухфазная растущая среда, а рост рассмотрен как деформация твердой фазы. В области биологического роста необходимо отметить обширную совместную работу большого количества авторов, занимающихся изучением роста тел, посвященную росту и ремоделированию (адаптация живых тканей) различных тканей и органов, в которой представлены основные имеющиеся на данный момент модели и сведения из области биологического роста [23].
Стоит отметить, что поверхностный рост тел является задачей, сходной с задачами механохимии, а именно: поверхностный рост тел может быть рассмотрен аналогично задаче распространения фронта химической реакции. Так, вывод уравнений, определяющих процесс роста, в представленном исследовании основан на развитии концепции тензора химического сходства для случая поверхностного роста. Подходы на основе тензора химического сродства, который может быть рассмотрен как аналог тензора поверхностного роста, управляющего процессами роста и перестройки тел, представлены в статьях А.Б. Фрейдина с соавторами [24, 25 и библиография в них].
Несмотря на наличие различных концепций и полученных результатов до сих пор не существует общепринятой универсальной математической модели, адекватно и полно описывающей механизмы роста и структурной перестройки тел, а также механохимических регуляций. В данной работе предложена модель поверхностного роста, основанная на принципах термодинамики и механики конфигурационных сил, и исследовано влияние механических напряжений, как одного из главных факторов, определяющих процесс. Кроме того, исследовано влияние ростовых деформаций в новом слое на поверхностный рост. Модель апробирована для решения задач поверхностного роста цилиндра, бруса и толстостенной цилиндрической оболочки.
1. Постановка задачии балансовые соотношения
Предполагается, что растущее тело состоит из диффундирующей и твердой составляющих. Поверхностный рост может быть рассмотрен как реакция на поверхности твердого тела, представляющая собой превращение диффундирующего вещества в твердое за счет работы клеток-строителей, находящихся на поверхности, в случае живой ткани, или за счет химической реакции. В зависимости от рассматриваемого процесса или уровня рассмотрения диффундирующее вещество может появляться в теле по различным причинам и различным образом: появляться в объеме тела (объемный подвод), заполняя собой некоторый предоставленный объем, или проникать внутрь тела вследствие диффузии через границу. Таким образом, новые слои появляются в результате превращения диффундирующего вещества в твердое тело на поверхности, где имеется соответственно сток и источник материала: B , ^ B + , где твердое вещество обозначится символом + , а диффундирующее символом * .
Пусть vt – текущая конфигурация растущего тела в момент времени t, а V0 – отсчетная конфигурация, зависящая от истории предыдущего роста. Внешняя граница тела Г является поверхностью роста. Линейные сегменты dx+ текущей конфигурации связаны с соответствующими в отсчетной градиентом деформации как dХ+= F. dX+ ;det F = V = ^, (1) где p + - парциальная плотность твердого вещества в области V, р+ - плотность твердого вещества на единицу объема в отсчетной конфигурации.
Кроме того, далее будет использоваться плотность диффундирующего компонента р0 - масса питательных веществ, приходящаяся на единицу объема V 0 конфигурации так, что р , dv =р0 dv 0.(2)
Элементы поверхности d to , d Q и единичные нормали n , N в актуальной и отсчетной конфигурации соответственно связаны следующим образом:
ndto= (det F)F-T-NdQ .(3)
Скорость роста v Г в актуальной конфигурации связана со скоростью роста V , в отсчетной и скоростью v + материальных точек B + как
-
v = dx+ (Xr (tX t) = 0 + v .(4)
dt
Также можно считать, что граница роста движется в направлении нормали к поверхности роста, т.е.
-
V, = WN ,(5)
где W – нормальная компонента скорости роста.
Для диффундирующего вещества введена скорость v , - скорость диффузии вещества к границе, «размазанная» по характерному объему твердого вещества. Тогда Лагранжева скорость диффузии V , 0 в отсчетной конфигурации может быть представлена как
-
V . 0 = F - 1 -C v . " v + ), (6)
где ( v . - v + ) - относительная скорость диффузии в актуальной конфигурации.
Запишем балансовые соотношения для рассматриваемого тела в условиях поверхностного роста под влиянием внешней нагрузки. В данной части записаны основные соотношения, необходимые для вывода тензора поверхностного роста.
Тело состоит из твердого вещества и диффундирующей составляющей, которая на границе превращается в твердое вещество в случае нарастания нового материала или образуется из твердого вещества в случае резорбции (процесс обратный росту). К телу приложены объемные и поверхностные силы, на границе роста может возникать скачок напряжений из-за нарастания преднапряженного вещества. Учитывая, что в данном исследовании рассматривается процесс поверхностного роста, наибольший интерес представляют балансы на границе тела.
Балансы массы, импульса и энергии были получены на основе причин изменения каждой из величин и использования транспортной формулы. Так, для изменения масс обоих компонентов транспортная формула выглядит следующим образом:
Dm? =if dP + +v '( p + v + ) d , Dt v ( d t )
Dm- =dp . +v '( p o v + ) I dv -
Dt V ( d t )
где масса твердого вещества m + = J p + dV и масса диф-
V фундирующего вещества m0 = J p0dV .
V
Причинами изменения массы системы являются объемный подвод вещества ц , , преобразование одного вещества в другое на границе, иначе – производство и сток на границе p 0 , p + , диффузия вещества, включающая частицы, подходящие к границе со скоростью V , 1 " , преобразующиеся впоследствии в твердое вещество, и частицы, покидающие растущее тело со скоростью V ex и не участвующие в реакции.
Таким образом, учитывая, что суммарное производство массы равно нулю, общий баланс массы на границы принимает следующий вид:
p + W + p 0 ( V . ex • N + W - V * " • N ) = 0. (8)
Аналогичным образом были получены балансы импульса и энергии. Среди причин изменения импульса имеются объемные и поверхностные силы, действующие на оба компонента, производство импульса на границе и в объеме вследствие превращения вещества, а также диффузия вещества. В результате общий баланс импульса на границе p+v+ + p0 v*" = -IS+ 1 • N - IS, 1 • N + p0 (v*" - vex )V° • N, (9) где IS+. 1 = S +", - S", - скачок напряжений на границе, записанный через тензоры напряжений Пиолы – Кирх-гоффа.
С учетом балансов массы и импульса баланс энергии записывается как p+ (и + + 2 v+ ) + p0 ( и. + 2 v*"2) =
= Р 01 v .]{ v .) V ex • N + h 0 • N + q Г-
- ( v +- I S + ] + v . " • I S . ] ) • N , (10)
где и +, - массовые плотности внутренней энергии; h 0 -вектор потока энергии; q Г - поверхностная плотность подвода энергии вследствие превращения веществ.
Учитывая полученные балансовые соотношения и второй закон термодинамики в виде неравенства Клаузиуса – Дюгема, а также обозначая массовые плотности свободной энергии Гельмгольца f + , = - Ts +, + и +, , определим поверхностную мощность диссипации:
D = -f р + ( f + 2 v + ) +р 0 ( f :+ 2 v 1 . " ) +
+ ( v +- I S + 1 + v . " • I S . ] ) • N - p 0 I v . ] (v .) V ex • N ) +
+ (1 -a ) q г . (11)
Более подробный вывод балансовых соотношений может быть найден в [26, 27].
2. Тензор поверхностного роста
Для последующего вывода предполагается, что все подошедшее к границе роста вещество преобразуется в твердое, т.е. отсутствуют частицы, покидающие тело и V ex = 0. Тогда выражение для диссипации вследствие математических преобразований может быть приведено к форме, содержащей нормальную компоненту скорости роста в виде общего множителя, а именно:
D = WAnn + (1 -a)q, (toAnn + q) > 0, (12) M+ где ANN – нормальная компонента тензора поверхностного роста, который, в свою очередь, имеет вид
A = — * ц * 1 - — + M + - J 2 ( v + - v in 2 ) + v Г ( v *n - v + ) j I , (13)
где тензор химического потенциала M + =
1 T
= f + 1--F + • [ S + ] и химический потенциал диффунди-
Р+ рующего вещества ц* = f* - N • Ff • S* • N / p*.
В случае квазистатики пренебрегаем последними слагаемыми и тогда
A nn = —-(- w + + F T :[ S + D + — * ц * . (14)
Р+
По аналогии с классической формулой физической химии [28], принимаем, что скорость реакции на поверхности определяется формулой
- ( A 1
го., = to 1 - exp(— NN ) .
N
J Rf )
Как следствие, нормальная компонента скорости поверхности роста определяется как
W = —- k * ( c ( Г ) - ceq ) , (16)
где c ( Г ) - концентрация вещества на границе, а ceq -равновесная концентрация, которая вводится таким образом, что A nn ( c = ceq ) = 0 [29].
Таким образом, для нахождения кинетики границы необходимо знать концентрацию на границе, которая может быть найдена из решения задачи диффузии, и равновесную концентрацию. В случае равновесной концентрации не происходит ни роста, ни резорбции и отсутствует реакция на границе.
Диффузионный поток задается законом Фика. Тогда в случае стационарной постановки и постоянного коэффициента диффузии уравнение диффузии принимает вид
A c + 5 = 0, (17)
где s – объемный подвод вещества, зависящий от напряженно-деформированного состояния. Граничное условие определяется балансом массы: все подошедшее к поверхности роста вещество преобразуется в новое.
В результате, скорость границы роста зависит от напряженно-деформированного состояния тела через выражение для равновесной концентрации, а напряже-но-деформированное состояние тела меняется за счет присоединения новых слоев в процессе роста.
В случае малых деформаций
-
w . П , (T ) + 2 ( £ + - £ gr ): C :( E + - £ gr ), (18)
где n+ ( T ) - объемная плотность свободной энергии твердого вещества при нулевых напряжениях; C – тензор упругости; ε gr – деформации в ростовом слое, возникающие в процессе присоединения нового вещества, которые могут быть нулевыми, ускорять или замедлять процесс роста в зависимости от рассматриваемого процесса и прикладываемой нагрузки. Влияние данных дополнительных деформаций на кинетику роста представлено в рассмотренных далее модельных задачах.
В результате нормальная компонента тензора поверхностного роста записывается как
A nn = M + ( Y ( T ) - 1 ( £ + - £ gr ): C + : ( £ + - £ gr ) +
Р + J 2
+ £ + : [ o + ! ) + RT In -^. (19)
c *
Таким образом, кинетика поверхностного роста для предложенной модели находится из уравнения (16) с помощью решения задачи диффузии и выражения (19) и зависит от напряженно-деформированного состояния, текущей конфигурации тела, подвода питательных веществ и ростовых напряжений в новых слоях. Данные величины также связаны между собой. Разработанная модель была апробирована для задач роста различных тел при различных условиях нагружения.
3. Поверхностный рост телпри различных нагрузках
Поверхностный рост цилиндра при сжатии. Рассматривается круговой цилиндр радиуса Rout под действием осевой нагрузки P . На границе цилиндра происходит радиальный поверхностный рост. Как было сказано выше, ростовые деформации могут быть равны нулю или отличаться от нуля и влиять на скорость роста. Если в ростовом слое имеются дополнительные деформации, то для нахождения напряжений и деформаций в теле необходимо решить следующую задачу:
V- ( С •• £ e ) = 0, r < R ;
0 (20)
V^(С••£e) = V^(С••£gr),r > R0, где R0 – начальный радиус тела.
В данной и следующих задачах функция подвода питательных веществ задавалась как функция от инварианта напряжений в виде, изображенном на следующем графике (рис. 1). Зависимость подбиралась таким образом, чтобы при равновесных напряжениях (напряженное состояние в теле, при котором не происходит роста) функция подвода была равна нулю. Данный вид зависимости является качественно наиболее приближенным по своему виду к экспериментальным данным по росту биологических тканей [30, 31]. Сравнение кинетики роста для других функций подвода, а также более подробное описание вычисления напряжений и концентрации в теле для задачи сжатия цилиндра могут быть найдены в [26].
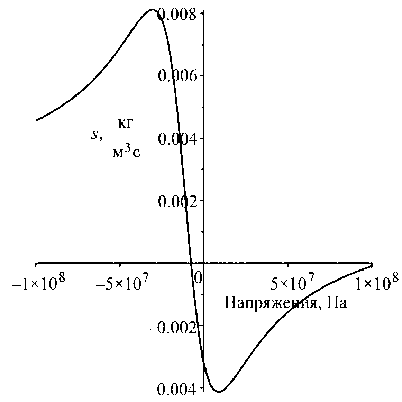
Рис. 1. Зависимость объемного подвода вещества от напряжений
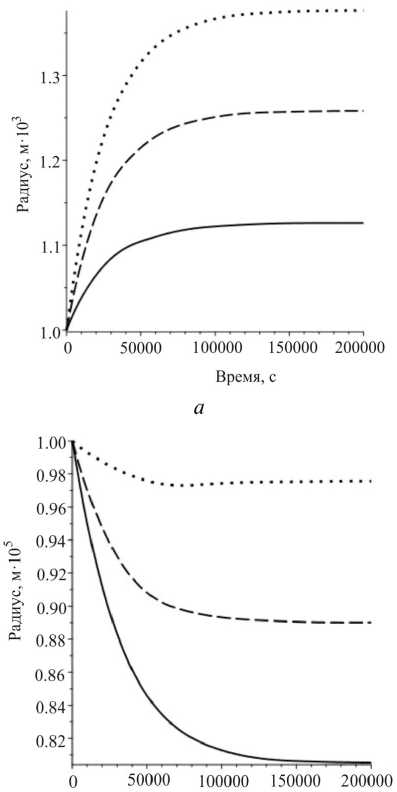
Время, с б
Рис. 2. Радиальный рост цилиндра при осевом сжатии различными силами: зависимость радиуса цилиндра от времени: а – для роста; б – резорбции
Fig. 1. Dependence of the volumetric supply of the matter on stresses
Для случая осевого сжатия осевые напряжения в теле вычисляются как
Fig. 2. Radial growth of the cylinder under axial compression with different forces: time dependence of the radius of cylinder for ( a ) – growth, ( b ) – resorption
^ z
P
"С
.
Ростовые деформации для случая осевого сжатия заданы следующей зависимостью:
Г г8; =-еg = kg ln -
где kgr – некоторый ростовой коэффициент.
Следующие графики (рис. 2) были получены для цилиндра при сжатии различными силами. Когда приложенная сила меньше, чем необходимо для поддержания равновесного состояния, начинается резорбция и радиуса цилиндр уменьшается. В противном случае наблюдается рост. Через некоторое время (несколько дней для данных графиков) достигается равновесное состояние для приложенной силы, когда тело перестает расти. Чем больше приложенная сила, тем больше достигаемый телом размер.
Также была рассмотрена кинетика роста при сжатии в зависимости от ростовых деформаций в нарастающем слое. На рис. 3 пунктиром изображен рост в отсутствие г g , т.е. при k 2g = 0, сплошными линиями - рост при различных значениях ростовых деформаций, причем ростовые коэффициенты к 1 > к 3 (нижние коэффициенты соответствуют номерам линий на графике). Как можно видеть, при этом изменяется скорость роста и величина достигаемого равновесного радиуса – радиуса, при котором тело перестает расти, адаптировавшись под приложенную нагрузку. Чем выше значение ростовых деформаций, тем больше достигаемый размер и меньше время выхода на равновесное состояние.
Поверхностный рост на верхней и нижней границах бруса при изгибе. К торцам бруса приложен изгибающий момент M . Одна часть волокон растянута, а другая сжата, соответственно, рост и резорбция происходят неравномерно.
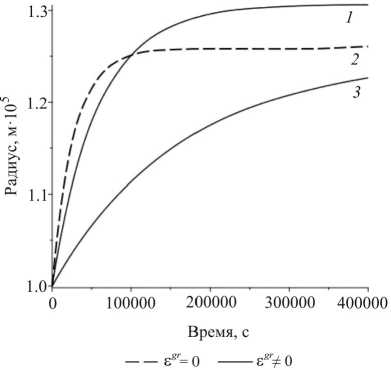
Рис. 3. Радиальный рост цилиндра при осевом сжатии при разных ростовых деформациях: для нулевых ростовых деформаций (пунктир) и ненулевых ростовых деформаций (сплошная)
-
Fig. 3. Radial growth of the cylinder under axial compression for different growth strains: for zero growth strains (dashed line) and nonzero growth strains (solid line)
Для роста в случае изгиба напряжения в сечении вычисляются как
, . M • r o ( r ) =-------------, (23)
I ( R out 1 , R out 2 )
где Rout 1,2 – расстояния от нейтральной линии до внешней границы сжатых и растянутых волокон соответственно. При нарастании нового слоя предполагается, что молекулы могут быть уложены более или менее плотно относительно предыдущего слоя, то есть могут возникать ростовые деформации в продольном направлении растущего слоя. Рассмотрена следующая зависимость ростовых деформаций от радиуса:
£ gr = k g-- r -----, (24)
R out 1 + R out 2
т.е. чем дальше от нейтральной линии, тем больше величина ростовых деформаций, а также имеется зависимость от общей толщины тела.
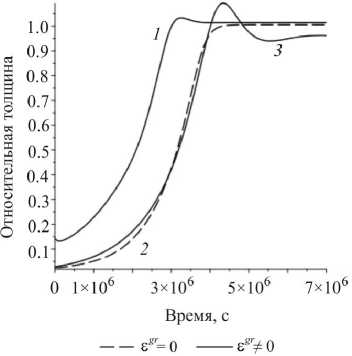
Далее аналогично случаю осевого сжатия приведены графики изменения относительной толщины балки (величина текущей толщины к равновесной, достигаемой через некоторое время) для роста без ростовых деформаций при различных значениях приложенного момента (рис. 4, а). Как видно, в зависимости от приложенного момента меняется скорость роста и монотонность роста, т.е. при определенных условиях рост может сменяться резорбцией. Чем меньше приложенный момент, тем быстрее тело выходит на равновесное состояние. И также был рассмотрен рост под действием одинакового момента, но при различных ростовых деформациях (рис. 4, б). Пунктиром изображен рост в отсутствие £gr, т.е. при к2g = 0, сплошными линиями -рост при различных значениях £gr, причем ростовые коэффициенты kg > к3Г. Здесь наглядно видно, что различная величина ростовых деформаций значительно влияет на рост тел, изменяя скорость роста, монотонность роста, а также достигаемый размер, обеспечивающий равновесное состояние при заданной нагрузке.
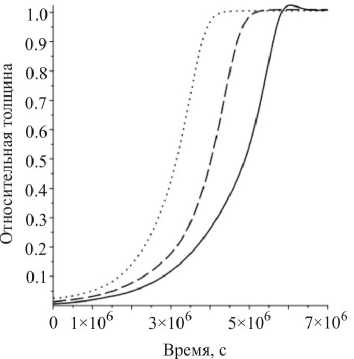
б
Рис. 4. Рост бруса при изгибе: зависимость относительной толщины от времени: а – для различных приложенных моментов; б – для нулевых ростовых деформаций (пунктир) и ненулевых ростовых деформаций (сплошная)
-
Fig. 4. Growth of beam under bending: dependence of the relative thickness on time ( a ) – for various applied moments, ( b ) – for zero growth strains (dashed line) and nonzero growth strains (solid line)
Поверхностный рост толстостенной цилиндрической оболочки. Рассматривается толстостенная цилиндрическая оболочка с внутренним и внешним радиусами Rin и Rout соответственно. На оболочку действует внутреннее давление p . Радиальный рост происходит на внешней границе оболочки таким образом, чтобы адаптировать тело к приложенному давлению. Напряжения в толстостенном цилиндре в отсутствие ростовых деформаций в новых слоях:
о r
R 2. - R 2 out in
• pR 2n
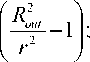
°ф = R 2,-R2 out in
( R 2,
• pRin\^u- + 1 1 .
I r )
а
б
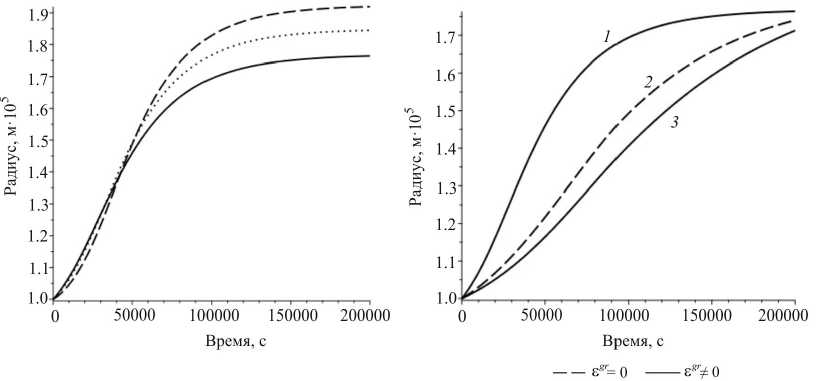
Рис. 5. Радиальный рост цилиндрической оболочки при воздействии внутреннего давления: зависимость внешнего радиуса от времени: а – при различных давлениях; б – для нулевых ростовых деформаций (пунктир) и ненулевых ростовых деформаций (сплошная)
-
Fig. 5. Growth of a thick-walled cylinder under internal pressure: dependence of the outer radius on time: a – for various pressures; b – for zero growth strains (dashed line) and nonzero growth strains (solid line)
Зависимость ростовых деформаций от радиуса выбрана аналогичной (22) в рассмотренной ранее задаче о сжатии цилиндра.
Далее приведены графики для поверхностного роста под действием различного давления (рис. 5, а ) и при разных ростовых коэффициентах (рис. 5, б ), аналогичные случаю сжатия цилиндра (см. рис. 2, а и рис. 3 соответственно). Стоит отметить, что для данной задачи растущее тело достигает равновесного состояния быстрее, однако необходимый для достижения данного состояния внешний размер тела больше, чем в случае сжатия.
Заключение
Выражение для тензора поверхностного роста было получено из общих балансов массы, импульса и энергии, и второго начала термодинамики в виде неравенства Клаузиуса – Дюгема. Развитая модель учитывает
Список литературы О моделировании поверхностного роста твердых тел под действием напряжений
- Manzhirov A. Some problems in mechanics of growing solids with applications to AM technologies // Journal of Physics: Conference Series. - 2018. - Vol. 991. - Р. 012056.
- Vandiver R., Goriely A. Differential growth and residual stress in cylindrical elastic structures // Philosophical Transactions of the Royal Society A. - 2009. - Vol. 367. - Р. 3607-3630.
- Truskinovsky L., Zurlo G. Nonlinear elasticity of incompatible surface growth // Physical Review E. - 2019. - Vol. 99. -Р. 0530001.
- Zurlo G., Truskinovsky L. Printing non-Euclidean solids // Physical Review Letters E. - 2017. - Vol. 119. - Р. 048001.
- Lychev S.A. Geometric aspects of the theory of incompatible deformations in growing solids // In: Altenbach H, Goldstein R, Murashkin E (eds) Mechanics for Materials and Technologies. Advanced Structured Materials. - 2017. - Vol. 46. - Р. 327-347.
- Лычев С.А., Манжиров А.В. Математическая теория растущих тел // Прикладная математика и механика. - 2013. -№ 77(4). - С. 585-604.
- Yavari A. A geometric theory of growth mechanics // Journal of Nonlinear Science. - 2010. - Vol. 20(6). - pp. 781-830.
- Механика растущих вязкоупругопластических тел / Н.Х. Арутюнян [и др.]. - М.: Наука, 1987. - 471 с.
- Маслов Л.Б. Математическая модель структурной перестройки костной ткани // Российский журнал биомеханики. - 2013. - № 2(60). - С. 39-63.
- Epstein M., Maugin G. Thermomechanics of volumetric growth in uniform bodies // International Journal of Plasticity. -2000. - Vol. 16. - Р. 951-978.
- Epstein M. The Elements of Continuum Biomechanics. -Wiley, 2012. - 392 p.
- Skalak R., Farrow D., Hoger A. Kinematics of surface growth // Journal of Mathematical Biology. - 1997. - Vol. 35. -Р. 869-907.
- Sozio F., Yavari A. Nonlinear mechanics of surface growth for cylindrical and spherical elastic bodies // Journal of the Mechanics and Physics of Solids. - 2017. - Vol. 98. - Р. 12-48.
- Goriely A. The Mathematics and Mechanics of Biological Growth. - New York: Springer Verlag, 2017. - 646 p.
- Vandiver R., Goriely A. Differential growth and residual stress in cylindrical elastic structures // Philosophical transactions of the Royal society. - 2009. - Vol. 367. - Р. 3607-3630.
- Ganghoffer J.-F., Goda I. A combined accretion and surface growth model in the framework of irreversible thermodynamics // International Journal of Engineering Science. - 2018. -Vol. 127. - Р. 53-79.
- Goda I., Ganghoffer J.-F., Maurice G. Combined bone internal and external remodeling based on Eshelby stress // International Journal of Solids and Structures. - 2016. - Vol. 94-95. - Р. 138-157.
- Louna Z., Goda I., Ganghoffer J.-F. Identification of a constitutive law for trabecular bone samples under remodeling in the framework of irreversible thermodynamics // Continuum Mechanics and Thermodynamics. - 2018. - Vol. 30. - Р. 529-551.
- Budday S., Steinmann P., Kuhl E. The role of mechanics during brain development // Journal of the Mechanics and Physics of Solids. - 2014. - Vol. 72. - Р. 75-92.
- Eskandari M., Kuhl E. Systems biology and mechanics of growth // Wiley Interdisciplinary Reviews: Systems Biology and Medicine. - 2015. - Vol. 7(6). - Р. 401-412.
- Gril J., Jullien D., Bardet S., Yamoamoti Y. Tree growth stress and related problems // Journal of Wood Science. - 2017. -Vol. 63. - Р. 411-432.
- Логвенков С.А., Штейн А.А. Механика формирования зоны роста в корнях растений // Российский журнал биомеханики. - 2010. - Т. 14, № 1. - С. 37-47.
- Growth and remodelling of living tissues: perspectives, challenges and opportunities / D. Ambrosi, M. Ben Amar, C. Cyron, A. DeSimone, A. Goriely, J. Humphrey, E. Kuhl // Journal of the Royal Society Interface. - 2019. - Vol. 16(157). -Р. 20190233. DOI: 10.1098/rsif.2019.0233
- Freidin A.B., Vilchevskaya E.N. Chemical Affinity Tensor in Coupled Problems of Mechanochemistry // In: Altenbach H., Öchsner A. (eds) Encyclopedia of Continuum Mechanics. - Berlin: Springer, 2020. doi.org/10.1007/978-3-662-55771-6_143
- Freidin A.B., Vilchevskaya E.N., Korolev I.K. Stressassist chemical reactions front propagation in deformable solids // International Journal of Engineering Science. - 2014. - Vol. 83. -Р. 57-75.
- Freidin A.B., Izmaylova Y.O. On a configurational force driving surface growth of solids // Materials Physics and Mechanics. - 2019. - Vol. 42. - Р. 582-595.
- Фрейдин А.Б. О тензоре химического сродства при химических реакциях в деформируемых материалах // Механика твердого тела. - 2015. - № 3. - С. 35-68.
- Гленсдорф П., Пригожин И. Термодинамическая теория структуры, устойчивости и флуктуаций. - М.: Мир, 1973. - 280 с.
- Freidin A.B. Chemical affinity tensor and stress-assist chemical reactions front propagation in solids // The American Society of Mechanical Engineers: in proceedings of the ASME 2013 International Mechanical Engineering Congress and Exposition. - 2013. - Р. V009T10A102.
- Effects of Mechanical Forces on Maintenance and Adaptation of Form in Trabecular Bone / R.Huiskes, R. Ruierman, G.H. van Lenthe, J.D. Janssen // Nature. - 2000. - Vol. 405. -Р. 704-706.
- Katti K.S., Gu Ch., Katti D.R. Anisotropic properties of human cortical bone with osteogenesis imperfecta // Biomechanics and Modeling in Mechanobiology. - 2016. - Vol. 15(1). - Р. 155-167.


