О моделировании систем очистки отработавших газов ДВС с использованием нейтрализаторов и тепловых аккумуляторов фазового перехода

В связи с неблагополучным состоянием окружающей природной среды в городах Российской Федерации органы государственной власти проводят политику улучшения экологических показателей автотранспортных средств. В нашей стране с 2006 года Постановлением Правительства РФ № 609 от 12.10. 2005 г. введены в действие международные экологические требования к колесным транспортным средствам: Правила № 83 ЕЭК ООН, Правила № 49 ЕЭК ООН и Правила № 24 ЕЭК ООН, значительно ужесточившие нормы эмиссии вредных веществ с отработавшими газами (ОГ) автомобильных двигателей [1].

Известно, что одним из основных методов обезвреживания ОГ двигателей внутреннего сгорания (ДВС) автомобилей является их каталитическая нейтра- лизация, осуществляемая путем пропускания ОГ через каталитический нейтрализатор (КН). Однако на определенных режимах работы дизельного двигателя эффективность КН может быть незначительной. В табл. 1 представлены экспериментальные данные, полученные В.Н. Ложкиным при испытаниях дизеля КамАЗ-740 по 13-тиступенчатому циклу согласно Правилам ЕЭК ООН № 49 [2]. Как следует из анализа опытных данных, наиболее низкая степень очистки углеводородов С Н и оксида углерода CO наблюдается в режиме холостого хода и на малых нагрузках. Это объясняется низкой температурой ОГ, недостаточной для начала реакции нейтрализации. Поэтому возникает проблема тепловой стабилизации матрицы каталитического конвертора на эксплуатационных режи- мах работы двигателя. Одним из альтернативных вариантов решения этой проблемы является использование теплового аккумулятора фазового перехода (ТАФП) [3,4]. Бортовой ТАФП обеспечивает температурную стабилизацию тепловых процессов путем «заимствования» недостающей или «сброса» излишней теплоты.

КН, совмещенный с ТАФП, состоит (см. рис.) из двух основных частей: собственно каталитического конвертора и ТАФП, объединенных в едином цилиндрическом корпусе 1. ТАФП включает в себя входной патрубок 2, диффузор 3 и теплообменник, состоящий из централь- ной капсулы, выполненной в виде цилиндра, и нескольких коаксиально расположенных заполненных теплоаккумулирующим материалом (ТАМом) цилиндрических капсул 4 с образованием между ними кольцевых зазоров 5. Цилиндрические капсулы 4 и кольцевые зазоры 5 имеют одинаковые радиальные размеры (толщину). Между цилиндрическим корпусом 1 и теплообменником находится слой тепловой изоляции 6. Каталитический конвертор включает в себя блочный реактор 7, «глухую» полость расширения 8 и выходной патрубок 9.

Таблица 1 - Выборочные технические и экологические показатели дизеля КамАЗ-740 на режимах нагрузочных характеристик по Правилам ЕЭК ООН № 49 с каталитическим нейтрализатором

й Он ^	N e , кВт	n дв , мин-1	т г , К	G Т , кг/ч	G B , кг/ч	G г , кг/ч	С сн , млн-1		сн , %	С со , млн-1		со , %
							До КН	После КН		До КН	после КН
1	0	800	373	1,8	159	161	80	80	0	270	210	22
2	10,2	1800	433	5,8	531	537	136	130	4	1230	730	41
3	25,4	1800	493	9,7	520	530	120	115	4	820	620	24
4	50,8	1800	573	14,7	523	538	135	125	7	840	500	41
5	76,3	1800	673	19,6	513	533	165	90	45	930	380	59
6	101,7	1800	813	25,4	510	535	380	100	74	3080	420	86
7	0	800	393	1,8	165	167	105	95	9,5	420	330	21
8	122,5	2600	833	34,2	764	798	386	90	76	1730	290	83
9	91,9	2600	738	26,9	762	789	150	75	50	780	170	78
10	61,3	2600	653	19,6	756	776	114	65	43	720	210	71
11	30,6	2600	573	14,0	747	761	105	75	29	870	180	45
12	12,3	2600	523	10,9	745	756	125	120	4	1110	1050	5
13	0	800	413	1,8	162	164	130	125	4	450	400	11

При разработке математических моделей функционирования системы КН-ТАФП использованы следующие основные допущения:

• 1.    В начальный момент времени 0 в период зарядки ТАФП ТАМ находится в твердом состоянии, а в период разрядки – в жидком, при этом его температура выровнена по объему и равна температуре фазового перехода Т _ф .

• 2.    В обратимых процессах фазового перехода ТАМа плавление-кристаллизация при 0 границы раздела фаз сформированы, температурное поле ТАМа в растущей фазе линейно, а

• температура исчезающей фазы равна температуре фазового перехода ТФ .

• 3.    Теплопроводность ТАМа в продольном направлении отсутствует.

• 4.    Процесс фазового превращения ТАМа принимается одномерным и моделируется чистой теплопроводностью. При этом границы раздела фаз неизменны по форме и в каждый момент времени представляют собой цилиндрические по-

• верхности, расположенные концентрично по отношению к цилиндрическим стенкам капсулы (вариант осесимметричной задачи).

• 5.    Коэффициенты переноса не зависят от температуры.

• 6.    Движение потока ОГ по каналам реактора рассматривается применительно к стационарному режиму работы ДВС как установившееся одномерное адиабатное течение газа.

• 7.    Для стационарного режима работы дизеля в каналах каталитического реактора устанавливается равновесный процесс между явлениями тепломассообмена и кинетики химических преобразований.

• 8.    Процесс теплообмена между стенкой канала и потоком ОГ осуществляется только по внешней поверхности активного слоя, т.е. теплообменом внутри пор пренебрегаем.

• 9.    Поток ОГ равномерно распределяется по всей совокупности каналов блочного каталитического реактора.

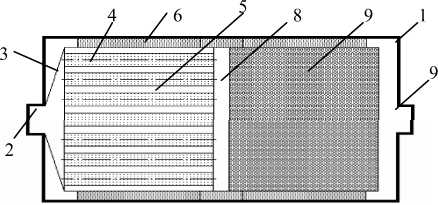
Рисунок - Принципиальная схема КН, совмещенного с ТАФП : 1 – цилиндрический корпус; 2,9 – входной и выходной патрубки;

3 – диффузор; 4 – цилиндрические капсулы с ТАМом; 5 – кольцевые зазоры; 6 – слой тепловой изоляции; 7 – блочный реактор; 8 – «глухая» полость расширения

Ниже представлена математическая модель функционирования системы КН-ТАФП на примере режима отдачи теплоты (разрядки ТАФП).

В процессе разрядки ТАФП часть отдаваемой им теплоты рассеивается в окружающей среде. Уравнение теплового баланса для ТАФП в этом случае имеет вид:

q г (т)= раз "  q ТАФП (^) ,           ⁽¹⁾

где: qГ (т) - тепловая мощность, полу чаемая потоком ОГ, Вт; qТАФП СО - тепловая мощность, отдаваемая при разрядке

ТАФП, Вт; _раз – энергетический КПД процесса разрядки.

Процесс конвективного теплообмена ОГ со стенками капсул при     0

описывается следующим уравнением: q тафпСО = а_г • Гц • [ Т ст (т) - Т ср (т)1 ,    (2)

где:   г – коэффициент теплоотдачи от стенок капсул к ОГ, Вт/(м2-К); Тст(т) - температура стенок капсул в момент времени , К; F – суммарная площадь цилиндрических поверхностей всех капсул, м2; Тср (т) - средняя температура ОГ в полости ТАФП в момент времени

т

вычисляемая по формуле:

Т ср (0 =

Т_вх +Т _ВЬ1Х(т) вх    вых

где ТВх , Твых (т) - температуры ОГ на входе и выходе из ТАФП, К.

Кроме того, при    0 справедливы сле- дующие уравнения:

Т _ф - Т _ст (т)

q ТАФП^{(т) -} ^Т               ^Г ц ;     ⁽⁴⁾

У СО qТАФП(О = рТВ- ГТ • У^  • Гц ,       (5)

d где: у(т)- толщина закристаллизовавшегося слоя ТАМа в момент времени , м;

^Т _Т ^В – коэффициент теплопроводности

К); ^Т_Т^В – плотность твердого ТАМа, кг/м³; r _Т – удельная теплота фазового перехода плавление-кристаллизация, Дж/кг.

Тепловая мощность q Г (т) при 0 определяется по балансовому уравнению qГ(т) = Gг -сг [Твых(Т)-Твх 1,       (6)

где: G _г – массовый расход ОГ, кг/с; с _г – удельная массовая теплоемкость ОГ, Дж/( кг∙К).

Система уравнений (1 – 6), в которых неизвестными функциями являются q Г (т) ,       q ТАФП (Т) , У Ст), Т вых (т) , Тст (т) , описывают процесс кристаллизации ТАМа в системе КН – ТАФП при следующих начальных и граничных условиях:

0 при t 0 .

q ТАФП ^{( 0) —} q Г ^{( 0 ) —} 0; 0< у (т)< 5т ; у ( 0 ) = 0 т ст ( 0 )« т ф ;

Твьк(0) = Т \ вых

Решением системы безразмерных уравнений (14)-(17) являются следующие

где – полутолщина капсулы, м.

Для аналитического решения вышеупомянутой системы уравнений введем следующие безразмерные комплексы:

- безразмерная температура нагреваемой поверхности капсулы

функции:

2;

^ст N Праз + 2. (Q + 1)’

Q = L J[( N -n

;

ст

Т Ф "Т ст (т)

^Т ф ^Т вх ^;

- средняя безразмерная температура ОГ в полости ТАФП

ср

A вых

ср

Т Ф - Т ср (т)

;

ф    вх

- безразмерная температура ОГ на выходе из ТАФП

ф    вых вых                  ;

Т _ф   Т _вх

р _аз + 2) 2+8- 1 ] ² -( N Лр _аз + 2)>

2 N раз ст

2 N _раз

_ 2- N Т]раз- (1-2. Ост )

2 N _раз

Они показывают, что процесс кристаллизации ТАМа в режиме чистой теплопроводности определяется тремя безразмерными параметрами – t , N и _раз .

-

безразмерная толщина закри-

сталлизовавшегося ТАМа в режиме чистой теплопроводности

Рассматривая внешнедиффузионную задачу гетерогенного катализа ОГ с учетом принятых допущений, можно получить функциональную связь между температурой стенки канала каталитического конвертора, разностью концентраций

t

N

а _г • у(^ _

ТВ ;

Т

- безразмерное время т- (а г. ) ² -( Т ф - Т „)

ТВ ТВ         ;

_{Т Т}   r _T

- число теплопередачи

_г F _ц

G г с г

После тривиальных алгебраических преобразований система уравнений (1 – 6) с учетом введенных соотношений (8 – 13) и краевых условий (7) сводится к решению следующих уравнений:

; ст       dt (14) ст ср     ст ; (15) 1    вых раз                 ; ср     ст (16) 0с = 0,5- (0ВЫх+1) ср          вых (17) с начальным условием

реагирующего вещества в ядре потока и у активной каталитической поверхности, а также на входе и выходе из блочного каталитического конвертора. Эта зависимость теоретически обосновывает сте-

пень конвертирования вредных веществ от теплового состояния конвертора [1, 2]

~ =T q^_.

ст     вх cгV

( С нач -С вых ) + ( С 0 - С 1 ) D a _г

где: Т_ст, Т . _вх - температуры соответственно стенки канала блочного конвертора и ОГ на входе в реактор (на выходе из ТАФП), К; q – тепловой эффект реакции, Дж/кг; с _{г V} – удельная объемная теплоемкость ОГ, Дж/(м³К); С ,^ , С .ых , С 0 , С 1 - концентрации реагирующего компонента соответственно на входе в реактор, на выходе из реактора, в ядре потока и у активной поверхности каналов реактора, кг/м³; D – истинный коэффициент диф-

В. Н. Ложкин, В. В. Шульгин, М. А. Максимов фузии, м²/с; а _г – коэффициент температуропроводности реагирующего компонента, м²/с.

Рассматривая изображенный на рис. КН как теплообменный аппарат, получаем уравнение теплового баланса системы КН-ТАФП:

Q Г     Q ТАФП    Q КАТ    Q ПОТ , (24)

где:   QГ – общее количество теплоты, получаемое ОГ при прохождении через систему КН – ТАФП за время , Дж;

Q _ТАФП – количество теплоты, отдаваемое ТАФП потоку ОГ при зарядке или получаемое потоком ОГ от ТАФП при его разрядке за время , Дж; Q _КАТ – количество теплоты, выделяющееся в блочном реакторе в процессе гететеро-генной каталитической реакции за время

, Дж;  QПОТ – суммарные тепловые потери КН за время , Дж.

Приведенная математическая модель функционирования системы КН-ТАФП позволяет исследовать и рассчитывать процессы отдачи теплоты и гетерогенного катализа. Она является основой для инженерной методики расчета подобных систем.

Рассмотрим пример вариантного расчета ТАФП в системе КН-ТАФП для городского автобуса ЛиАЗ-5256 с механической коробкой передач и дизельным двигателем КамАЗ-7408.10. Путем численного расчета городского цикла на дороге для городских автобусов, заданного согласно ГОСТ 20306-90 графической зависимостью V_A (скорость) – S_A (пройденный путь), можно получить среднеинтегральные значения температуры и расхода ОГ, характеризующие реальный режим работы ДВС в режиме городского автобуса. Они являются наиболее вероятными величинами и представляют собой основные исходные параметры утилизации отходящей теплоты ДВC, предназначенные для теплового расчета ТАФП и некоторых других теплоутилизационных агрегатов, а также для выбора ТАМа. Так, при температуре окружающего воздуха Т 253 К они составляют: массовый расход отработавших газов -

Gграсч = 345 кг/ч, их температура – Тграсч = 510 К. Приведем величину Т расч к температуре Т 296 К (при этой температуре были получены экспериментальные данные, представленные в табл.). Для этого используем приближенную формулу, полученную А.А. Сорокиным в работе [5]: лет tзим = tv к _ (Т лет _ тзим),        (25)

^г             лет        ^{0        0}

T ₀ зим

T ₀

где: t _г ^им , t _г ^лет – температуры ОГ соответственно в зимний и летний периоды, ºС; Т ₀ ^зим , Т ₀ ^лет – температуры окружающего воздуха соответственно в зимний и летний периоды, К; к – коэффициент, учитывающий увеличение удельного расхода топлива при зимней эксплуатации.

Полагая к 1 , по формуле (25) получаем: Т ˆ _г^расч 576К при Т^лет 296 К. Исходя из значения Т ^ˆ _г^расч 576 К, выбираем ТАМ – гидроксид натрия NaOH , основные теплофизические свойства которого представлены в табл. 2.

Зададимся геометрией теплообменника, изображенного на рис.: r1 20 мм,  r2  25 мм,  r   35 мм,  r4  40 мм, r 50 мм, r 55мм, r 65мм, r 70 мм,  r  80мм,  r   85мм,  r   95 мм, r 100 мм, где r – расстояние от оси центральной капсулы до цилиндрической поверхности «кольцевой» капсулы.

Примем, что при работе дизеля КамАЗ-7408.10 на холостом ходу ТАФП должен подогревать его ОГ, поступающие  в  ТАФП, от   Т _вх 373К до

Твых  553 К. Отдельным расчетом опре деляем, что коэффициент теплоотдачи от стенок капсул к ОГ аг =62,4 Вт/(м2^К). Тогда необходимая безразмерная температура ОГ на выходе из ТАФП 0ВЫх = Тф ТТвых = 572-553 = 0,0955 , (26) вых   Тф  Твх   572  373

средняя безразмерная температура ОГ в полости ТАФП.

О = Т ^—ср^ ₌ ^{572 463} ₌ 0 , 547, (27)

^ср     Т _ф   Т _вх    572  373

а максимальное значение безразмерной толщины закристаллизовавшегося ТАМа

Q =

а г-y (т) _ 62 , 4-0 , 005

ТВ

Т

Приняв

1 , 8

= 0 , 173 .

I_раз = 0 , 9 и решая совме-

стно ст

уравнения (19) и (22) относительно и N , получаем:   0_ст = 0 , 0803,

N = 2,15. Зная Ост =0 , 0803, по формуле (8) вычисляем Т _ст 556 К. Из уравнения (13) вычисляем значение площади поверхности теплообмена:

F ц

G_r -с _г N _ 161-1024-2 , 15

г

3600-62 , 4

= 1 , 58 м 2 .

Таблица 2 – Основные теплофизические свойства гидроксида натрия NaOH

Наименование теплофизической величины и ее размерность	Численное значение
Температура фазового перехода плавление-кристаллизация, К	572
Удельная теплота фазового перехода, кДж/кг	393
Плотность в твердой фазе, кг/м3	2130
Плотность в жидкой фазе, кг/м3	1780
Коэффициент теплопроводности в твердой фазе, Вт/(м∙К)	1,8

Наконец, разрешая уравнение (20) относительно t , получаем, что безразмерное время полной кристаллизации ТАМа при выбранных параметрах составит t 0,314 . Из уравнения (12) вычисляем физическое время полной кристаллизации ТАМа :

ТВ ТВ t Т Т   rT т           ~                      ...

(ОС г ) ² "( Т ф - Т вх )

0 , 314-1 , 8-2130-393000

...                                     611 с.

62 , 4 2 -( 572-373 )

Исходя из принятой геометрии теплообменника и значения F = 1 , 58 м², окончательно определяем, что его длина должна составлять 410 мм.

Таким образом, размеры ТАФП практически сопоставимы с размерами штатного глушителя шума.