О моделировании вынужденных колебаний в электрических цепях

Под колебаниями в настоящее время понимается повторяющийся процесс изменения состояний системы около точки равновесия. Колебания в электрических цепях классифицируют по физической природе (механические, электромагнитные, тепловые и смешанного типа) и по характеру взаимодействия с окружающей средой (вынужденные, свободные и затухающие колебания). В данной работе будут рассмотрены лишь вынужденные колебания.

Все контура содержат электрическое сопротивление R. Процесс независимых колебаний в этом контуре уже не подчиняется гармоническому закону. За любой период колебаний часть электромагнитной энергии, запасенной в контуре, преобразуется в джоулево тепло.

Если колебательный контур содержит генератор с периодически изменяющейся ЭДС, то в нем устанавливаются вынужденные колебания. В случае если ЭДС источника тока изменяется по закону

E(t) = Е_о cos(wt) (1)

то дифференциальное уравнение вынужденных колебаний в последовательной RLC -цепи записывается в виде:

q + 2pq + w²q = E cos(wt) (2)

Это уравнение аналогично уравнению вынужденных колебаний пружинного маятника. Его единое решение представляет собой необходимую сумму двух слагаемых - совместного решения однородного уравнения и частного решения неоднородного уравнения. При этом общее решение однородного уравнения описывает затухающий переходный процесс, по истечении которого в системе устанавливаются вынужденные колебания. Данные вынужденные колебания будут происходить по закону:

q^ = -w

^Е о

' JR2+(wL-w?C)

= cos(wt + ф)

. 2

Где ф определяется формулой:

Ф = arctan

R

wL

^— ^^^^H wC

- (4)

Зная закон изменения заряда q(t), легко найти I(t):

закон изменения тока

I(t) = - w

^Е о

' JR2+(WL-^'

= cos(wt + 0 ) . 2

где введен угол 0, равный 0=-(ф+п2). Угол 0 показывает отставание колебаний тока I(t) по отношению к колебаниям напряжения источника питания E(t)=E0cosot.

Амплитуда тока I0 и сдвиг фаз 0 определяются формулами: wL-Д

7 _о = у , ^ = arctan —^^ (6)

Величина Z = Jr² + (wL — -^) ² называется полным сопротивлением или импедансом контура. Она состоит из омического сопротивления R и реактивного сопротивления ωL-1ωC Импеданс колебательного контура в комплексной форме записывается как:

Z = fi + i(w ^L --)

амплитуда установившихся

Из полученных формул видно, что колебаний тока будет максимальной когда oL = 1)С или 60 = бо0 =

VL? (8)

При этом условии в колебательном контуре наступает резонанс. Резонансная частота ω0 равна частоте свободных колебаний в контуре и не зависит от сопротивления R.

Формулу для амплитуды тока вынужденных колебаний можно преобразовать, выделив в явном виде зависимость от отношения частот —, «о где )о

-

резонансная частота. В результате получаем:

^ 0

Е о ^С

^С+^~^

6о —

На рисунке 2 изображен программный  код, написанный в программном средстве Matlab, для построения графика затухающих колебаний.

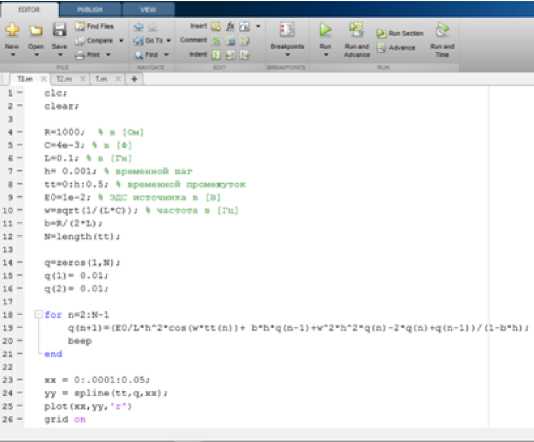
Рисунок 2 – Программный код для построения графика

На рисунке 3 представлено изображение затухающих колебаний, смоделированное с помощью программного средства Matlab.

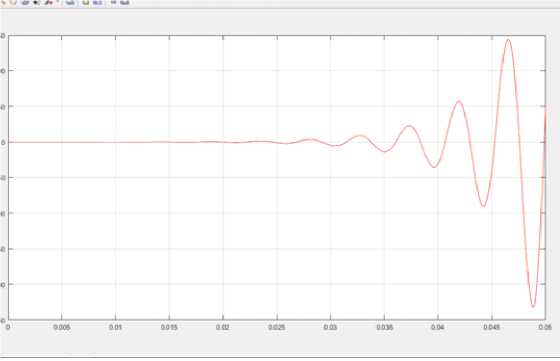
Рисунок 3 – Изображение затухающих колебаний

Таким образом, в ходе данной работы были изучены и смоделированы вынужденные колебания в электрической цепи. Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.