О моделях повреждаемости реономных регулярных структур

The linear rheonomous statement constitutive relations for an inhomogeneous medium with explosive on coordinates by material functions are considered. The evolutionary destructionis taken into account by introduction to constitutive relations of a tensor destruction. By an average technique the algorithm for a solution of the quasistatic problems of composite mechanics with the accepted constitutive relations is described.

Операторные определяющие соотношения, учитывающие меру повреждаемости, были рассмотрены нами в работах [1, 2]. Материальные функции определяющих соотношений для неоднородных сред зависят от пространственных: координат и для композитов являются разрывными функциями этих координат. В работе [1] подробно проанализирован простейший случай физически линейной реономной среды, а в работе [2] рассмотрены и некоторые нелинейные среды.

Пусть нам заданы выражения напряжений а,_у через деформации е и повреждаемость %_/У в виде

О и = /ГунО,') ef-A^W + J^yH(M ) %н (т) сИ . (П О

Соотношения (1) являются частным случаем общих операторных соотношений 1 ]. При этом для тензора повреждаемости % (z) запишем выражен ие

Хи = Р". ;     ) eL(C)(2)

О

Для сокращения записи воспользуемся символическим операторным обозначением [3] и запишем соотношения (1) в виде

= Г.уы е^ + а соотношение (2) в виде

Из (3) и (4)

°i j = У к ’ dijkl = VljHW V iJmn Xmnkl( 5 )

т.е. мы получили соотношения, формально совпадающие с соотношением классической теории термовязкоупругости [4]. Заметим, что традиционно в соотношениях (2) тензор повреждаемости связывают с напряжением [5]

Хи= J^yH(^t)a„ (т ) dx ^УцкЮ ,.,.

О

Подставив (6) в (3), получим

СУ I j = Г j ki Е        i j т и У w н к / СУ/)

Введём единичный тензор четвёртого ранга А [6],

Тогда (7) можно записать в виде

• (    Д/ у у у       i; т п ^ ,;’О' ) С> у у — Ту/ к I Е у.у .(9 у

• Пусть тензор-оператор 1Т Н является обратным по отношению к оператору, заключённому в левой части (9) в круглые скобки, т.е.

• (    ^i ; к I              »kt ) ki РЧ " ру -(10)

Тогда соотношения (9), а значит и (7) можно, как и прежде, записать в виде (5)', только теперь оператор Sijki имеет вид не (5)², а

Sijki — IT; у т л Г т лк I .                                                    ( I ■ )

Таким образом, доказана эквивалентность записей (2) и (6).

Разумеется, мы будем считать определяющие соотношения (5) обратимыми, г.е. их можно разрешил, относительно деформаций

<у=(Гю^/>U -I где

Sa».» Qmnk!-^,ki •(13)

Определяющим соотношениям (12) соответствуют две исходные формы записи:

Е.к=Кик1Си4-А,!к, Хк,-<14)

Одна форма в виде (6), а другая в виде (4). В первом случае

Qi ;к 1      1 I + А, /ШЛ V тпЫ , а во втором

Q, iki ~В: in-n К .uni’ , где т.е.

тензор-оператор B_ijki является обратным к тензору-оператору ,\_ик1-Л1_кт>К-

В ijkl ^klmn ~^klpq X рчтп)-^! jmn •

Таким образом, и в случае (14) обе формы записи (4) и (6) эквивалентны. Для изотропного случая соотношения (14) могут быть записаны в виде

с./ ^KSij +^ Ха , v 1 v; о

6^Г= К^ ат- Л1 % .

где

£7, = 67аг, + е,

G=cSu + .< , х.. = ~Х <Х, X б’ =е,,-ЗаД, о

-6

. _{5 +}1 к ( 8 8, + б,, 8 J, с j Kt                     х i л J *            I • i к z

Соотношения (6) в этом случае примут вид

О ^

где аналогично (20):

V У,-ЗУ         1 -

— Wj^t^.o,,:) ф...

Поэтому соотношения (12) могут быть записаны в виде

ег

Так что для этого случая

Опишем теперь, каким образом можно отыскать экспериментально ядро О Ui. соответствующее оператору Q в (23). Для простоты будем считать ядро Q разностного типа QU-т), а форму записи (23) - соответствующей форме Больцмана - Вольгерры, т.с. в виде интеграла Стилтьеса:

О

При этом из (24) следует

0(0 = К(1)д- {лф-тИУСт).                 (261

О

Эффективные ядра релаксации

Стремление расширить область применения феноменологического подхода к описанию деструкции материала с учётом его структуры за счёт введения новых параметров (моментных напряжений, дислокаций, объектов повреждаемости) связано со многими причинами. Это не только учёт концентраторов шероховатости поверхности, надрезов, отверстий и т.п., но и наличие неоднородности структуры. Будем считать, что эта неоднородность носит регулярный характер, т.е. материальные функции определяющих соотношений (1) предыдущего раздела являются периодическими функциями координат. В этом случае разработан достаточно эффективный аппарат методики осреднения [7,8]. Этим аппаратом мы и воспользуемся для описания деструкции композитов в процессе их деформирования.

Рассмотрим, например, изотермический случай подобных определяющих соотношений. Уравнения равновесия среды запишем в виде

Вводим малый геометрический параметр а [7] и, считая ядра .S’, ,.Д1) операторов San (4) (пред, раздела) функциями быстрой переменной £ [8].

а запишем уравнения равновесия (1) в виде

-- б / ; Щ / U^ , + 5 , , Г, И , + р /с =^: 0 .                            ( 3 ) а ''

Вектор перемещений и(х,с) представим в виде асимптотического ряда по степеням о :

M^v^-t-aN^ v_{m i} 4-a' . + a ³ Лц,v             (4)

и               ст^: > ст¹1

где “локальные” операторы N (с), А' (£), А (£) зависят со быстрой переменной, а “среднее” поле перемещений v(x) - от координаты х. Тогда дифференцируя (4), имеем

и(П          / °

^Uk.l = V_t j-^Nkmi.'l V_m>. +а Л' ⁽^„_ivi, V,,,^ + Л' V^i,'

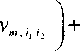
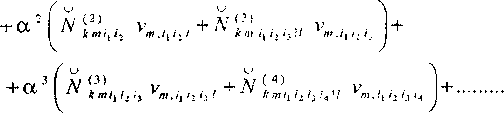
< I И                   vj ( 2 )                          u ( 21

+ «| N^i. v_milj + Ni„,_w.i v,„_J|l2, + ЛГ^м,

+a Nkml,l_t V,    + Nkml v •    , +

A kmi. V„,ilitisi + Nkmi^r=

+(6)

Подставим теперь разложения (5) и (6) в (3) и соберём слагаемые при одинаковых степенях а. Тогда получим

। А-')        А0'               аО)

—Semi, v_{m Л} +Si_mill, v,_n, , +aSimi,*a Si^ki.^^ v_{mJ l j iii} +...-*-рА =0, (/)

где определены однородные тензоры - операторы: Si_mil =0, Stmij,             _: т.е.

операторы, нс зависящие от координат , б/™,— 5;дя/,+5^шУ^^ =0 ,(8)

• 5,S. NNk™?ji н- S^.N^i, j                  ,(9)

C^S^N^,, j, CO)

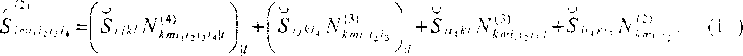
Проводя осреднение в правых частях выражений (8)-(11), т.е. интегрирование по ячейке периодичности, и учитывая, что в силу периодичности структуры осреднение от производной равно нулю [7], получим

л(°1 /и         .            \

8т„1ЧЦ8^Ы^+5иЛ, лС) /и            и „ \

SimiM Ц^ИзИ^Ьт,,^*5”-»11^- Nkm,, j ’

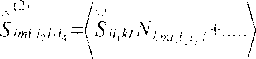
и т.п.

ГО) „          ЛГ2)

Для определения тензоров-операторов S> >ц , S,^ь,,, S,it;,„„.... необходимо найти локальные операторы Nщ , N^: , К,;нт , ...... для чего требуется решить задачи на ячейке периодичности, которая определяет структуру рассматриваемою композита.

Система уравнений для этих задач выписывается из соотношений (8)-( 10):

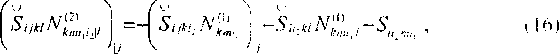
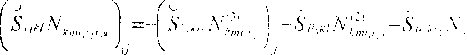
Итак, зная структуру композита, мы из решения задач (15), (16). (17) определяем локальные ядра релаксации NV1 (£, ?) ,      fq. г) ,      (^, г) .   Операцией осреднения но ячейке периодичности мы по формулам (12)-(14) находим “эффективные" ядра релаксации S^’'H(f), 8‘;н„,(г), S^im„(.O, .....

Если теперь мы в качестве определяющих соотношений в формулах (I). (3) первого раздела используем соотношения (1) первого раздела с ядрами релаксации Г/Н(х,?), которые предполагаются нами также периодическими функциями координат, то, повторяя все выкладки, проведённые в этом разделе, мы найдём эффективные ядра релаксации ГА, (?) , Г/^/m Ф) , Г/ф, „;„ (?) , ........

Заметим, что определение указанных эффективных ядер связано с решением уравнений равновесия (I).

Чтобы найти эффективные ядра, описывающие определяющие соотношения (5) первого раздела, связывающие тензор повреждаемости у„ с тензором деформации г . нам. строго говоря, нужно рассмотреть кинетические уравнения для величин у . Однако мы примем в качестве гипотезы, что процедура осреднения, описанная в данном разделе, применима и для тензора повреждаемости у . Применяя ну процедуру, мы найдём эффективные ядра А',¹ *’2. (г), А *;,„. (?), 8:'8._ir(i U). .......

Эффективные ядра Ед-'/ (?) , У'^_т1. (?) находятся из операторного соотношения:

Ё = ( р - Г )-А . JE = Е .                         (18)

где А - оператор, обратный к оператору' V , т.е.

}^z(r-TW^               091

О

,                        (20)

о где ^к,тп " единичный тензор шестого ранга:

К сожалению, найти единичный тензор нечётного ранга не удаётся, и поэтому не удаётся найти эффективные ядра ^У^т (?) •

Так что, если мы считаем, что моментные напряжения могут возникать только за счёт неоднородности материала, то в качестве таких моментных напряжений: можно выбрать макроскопические напряжения, определяемые операторами S, или

Эффективные ядра ползучести

Примем теперь за основу изотермический вариант определяющих соотношений в форме (11) (первый раздел). При этом будем считать, что тензор повреждаемости ^ связан с тензором напряжений соотношением (5) первого раздела. Если композит является ршулярной структурой. то ядра ползучести Q_ijk, (х, /) и K_ijH (х, /) являются периодическими функциями координат, и мы в праве и тут применить разработанную в [7] технику осреднения.

Будем считать для простоты, что объёмные силы отсутствуют. Тогда уравнения равновесия (1) второго раздела удовлетворяются тождественно, если ввести симметричный тензор функций напряжений ф по правилу

Уравнения совместности деформации [3]:

П„ =егр„е„„е „.„,-0                          (2)

после подстановки в них соотношений (11) первого раздела и (1) приобре'гут вид

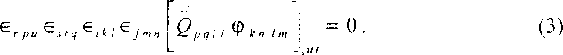
Если бы операторы Q^.avi зависели от координат ( Q^,= Q ). то уравнения (3) можно было бы записать так:

В , , . Ф ,    =0 ,                                                (41

где

• В.    s к                         i к Ф/ т п 2 / у i ¹

Рассмотрим асимптотическое разложение тензора ср (1) по малому параметру а:

Ф ₆ „ ~ ЧЛЛ а М*" ¹> о ¥н», + а ² Мк „ t.,,.. *

(Л

"К Ct Мк п к\ р- iv iL i. У ( .^      , T (X М к г к р /7 /. -4 ф^

где М , а = 1, 2,3,- локальные операторы, зависящие от быстрых координат Е

• (2)    (раздел 2), а у . - гладкая тензор-функция, зависящая от координат х .

Дифференцируя (6) по координатам, имеем о И)                            ( и (I )(2 )

ф , = ЧД„ / + Мкнк, и, 1,4 У^ Я| + ОС М к пк1П}           , + К4к и    i I к ,' +

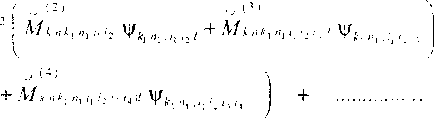
+ «' I Мк.к,.

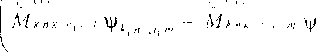
Ф«„,,_т -W n.im 7    Mkiik.,,,!, !т ф,

О'

Фкя,.. ^Мк_як_1П1._;121₅м                                                        .

Представим теперь тензоры деформаций £ и напряжений ст в виде разложения по ммому параметру а:

ст,^—Т;;'Чт'1’Чатр'+а2т’:Л(9)

а

Из (1), (8) и (9) следует, что т:=е;к1е,,„я |                   а            М t                 - v (2))

+ Мкпкх и, /, >,\1т Х)/^,

^Т;У -^Gikl^Gjm_n уМкпк_хя_х1_х V^n,.,^,,, + Мк„к_х„,1₁АЛ >У_к.,_П1.ц1_1т +

V (2)                      v <ТА

А"Мк nk_v n_xi_xi_T\m Х|^ ^    / 4- Мknl_xn_x'_xi₂i_xijm ЧА _и- I ,

^И^.к^ипп Мк„к_х._чМ1 V _{tl 2}/_m + Mk«k_ir,,_vi,.,,Al\\S_tv

у (3)                         u(4)

4- М к rt^ ^И1 6 (’ '3 \^т¥^             ^Mk"^t-'^,>‘^!

^ >:т ^к, nx,ixi.

Введём тензоры-операторы Тцк,^!^.„л.., (а = -1,0,1,2,.......) по формулам

^(-’)                        о (1)

Tijkv«xix — ^-ikt^imn ^кп кх »х ix\i т х

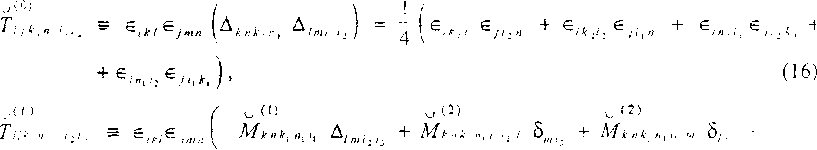
+ Мкпк,

т.

= е<к1е,т^, Mk,lkxnxi i. A.lm aV ^ин ^кн к , Пх 1 - к i ;|ш 5,

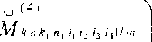
Используя операторы (15)-(18), соотношения (11)-(14) можно записать в виде

4n'Bt« =7’^—: ^,„,,/j; =e^e,,„. ^z.„.,-„, ,            120)

T^ = Tyk, ^

Тогда

u(2)

T ijk1nli1

Y^’ =            - р =      0,1,2,....... (23)

• (1 )                        :

Чтобы найти локальные операторы ползучести М , М ......... нужно воспользоваться уравнением (3) или (Г). Имеем из последних:

e_rpae,,_g f-+ а²<' +1   - о. (24)

или. подставляя в (24) определяющие соотношения (23), получим

6rPU^,q ^a"VQpqi. т(,;' \  =0.125)

n=--L\

Принимая во внимание (19)-(22), имеем для (25)

т';п = —7       .....M"V|, , . , - — Так., , Vt „ .,+- а'                                         а■ ■

+ -                                                 а = -1,0.1,2,(26)

Производные от операторов Т , входящие в (26) легко определяются из выражений (15)—(18), которые можно записать сокращенно в виде

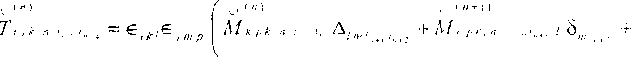
, . ( л 1 ))

4" Л/ к р кх п, ix         5у -       Мк pkn^i . .+       1 *( — )

где а = - 1,0. 1,2, ., при этом

М = 0 ; М s Д ( Л/*-,,*-,,,, = ДЬ1к п ).

Итак, процедура осреднения позволила полностью описать алгоритм решения квазистатических задач механики композитов, определяющие соотношения компонентов которых подчиняются законам линейной теории вязкоупругости с учетом эволюционной деструкции.

На основе этого алюритхш можно рассматривать конкретные композиционною структуры: слоистые, волокнистые, слоисто-волокнистые и т. и. [7]