О модификации быстрого одномерного преобразования Фурье по алгоритму Кули-Тьюки
Автор: Сидорова Т.В., Зыкова Т.В., Сафонов К.В.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 2 т.16, 2015 года.
Бесплатный доступ
Рассматривается один из методов нахождения дискретного преобразования Фурье, позволяющий уменьшить затраты машинного времени на вычисления по сравнению с классическим алгоритмом. Быстрые алгоритмы вычисления преобразования Фурье очень востребованы и актуальны, они имеют множество приложений в задачах цифровой обработки одномерных и многомерных сигналов, обработки различных изображений, например космоснимков. Общепринятый алгоритм представляет собой последовательное вычисление одномерного дискретного преобразования Фурье по строкам и столбцам. Существуют различные методы ускорения данного алгоритма, один из которых и реализован в данной статье. Представлена программная реализация модифицированного алгоритма по аналогу Кули-Тьюки дискретного преобразования Фурье для одномерного сигнала с числом отсчетов p · 2 s, p, s N. Для данного алгоритма была разработана программа в системе компьютерной математики MATLAB. Она протестирована на наборе, состоящем из 16384 отсчетов одномерного сигнала. При выполнении программы производится также сравнение времени ее выполнения со временем, затрачиваемым встроенным алгоритмом вычисления быстрого преобразования Фурье. В результате, среднее время выполнения программы по модифицированному алгоритму дает выигрыш около 20 % по времени. Кроме того, приводится общее описание алгоритма дискретного преобразования Фурье, обозначены возможности для увеличения скорости выполнения вычислений, рассматривается модифицированный алгоритм по аналогу Кули-Тьюки быстрого преобразования Фурье для одномерных и многомерных сигналов.
Преобразование фурье, быстрое преобразование фурье (бпф), алгоритм бпф кули-тьюки, программируемая логическая интегральная схема (плис)
Короткий адрес: https://sciup.org/148177426
IDR: 148177426 | УДК: 519.677
Текст научной статьи О модификации быстрого одномерного преобразования Фурье по алгоритму Кули-Тьюки
Введение. Дискретное преобразование Фурье (ДПФ), одномерное и многомерное, имеет множество приложений в задачах цифровой обработки сигналов, например, ДПФ можно использовать для спектрального анализа многомерных сигналов, для обработки космоснимков. Общепринятый алгоритм, который лежит во всех стандартных пакетах обработки сигналов, представляет собой последовательное вычисление одномерного дискретного преобразования Фурье, так называемый алгоритм «по строкам, по столбцам». Существуют различные методы ускорения данного алгоритма – быстрое преобразование Фурье. Самой распространенной реализацией быстрого преобразования Фурье является алгоритм Кули–Тьюки. Модификации данного алгоритма позволяют сократить время выполнения вычислений быстрого преобразования Фурье. Увеличение скорости выполнения алгоритма можно получить путем изменения основания алгоритма Кули–Тьюки: вместо основания 2 берут 4, 8, 16 и т. д., а также использованием параллельных вычислений.
В работе создана программа в среде MATLAB модифицированного алгоритма Кули–Тьюки для сигнала с числом отсчетов p • 2, p, s е N. Число операций в этом алгоритме меньше, чем при непосредственном вычислении дискретного преобразования Фурье, что позволило сократить время выполнения программы по сравнению со встроенным алгоритмом [1–3].
Быстрое преобразование Фурье на основе модифицированного алгоритма Кули–Тьюки. Дискретное преобразование Фурье периодического дискретного сигнала x ( n ) с периодом N определяется как
N - I 2 П i nk
X ( k ) = £ x ( n ) eN , k = 0, 1, ..., N - 1. (1)
n = 0
Функция X (k) является периодической функцией по аргументу k с периодом N. Дискретное преобразование Фурье представляет собой N отсчетов спектра, взятых на периоде с интервалом дискретизации 2n по частоте, равным NT . Для больших значений N прямое вычисление по выражению (1) требует выполнения весьма большого числа арифметических операций умножения и сложения, что затрудняет реализацию вычислений в реальном масштабе времени.
Быстрым преобразованием Фурье называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности дискретного преобразования Фурье [4]. Основная идея быстрого преобразования Фурье состоит в том, чтобы разбить исходный N-отсчетный сигнал x(n) на два более коротких сигнала, ДПФ которых могут быть скомбинированы таким образом, чтобы получить ДПФ исходного N-отсчетного сигнала. Так, если исходный N-отсчетный сигнал разбить на два
N
отсчетных сигнала, то для вычисления ДПФ каждого из них потребуется около
N
— I комплексных умно-
жений. Тогда для вычисления искомого N -отсчетного
( N Y
ДПФ потребуется порядка 2 1 — I
N 2
комплекс-
ных умножений, т. е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо f 1 -отсчетного ДПФ два -отсчетных ДПФ и сокращая тем самым
f 4 )
объем вычислений еще в два раза. Существует большое количество алгоритмов БПФ, однако все они являются частными случаями единого алгоритма, базирующегося на задаче разбиения одного массива чисел на два. Наиболее распространенным алгоритмом является алгоритм Кули–Тьюки [5] и его аналоги [6–9].
Алгоритм Кули–Тьюки по основанию 2 работает следующим образом. В этом случае количество отсчетов в выборке функции должно быть кратно степени 2. Выборка делится пополам, далее каждая половина делится на две части. Продолжается данный процесс до тех пор, пока не останутся два элемента, для которых реализуется преобразование Фурье. Таким образом, при вычислении одномерного дискретного преобразования Фурье длиной N необходи-
N мо выполнить — ■ log2 N двухточечных ДПФ, каждое из которых требует одно комплексное умножение и два комплексных сложения.
Двумерное разбиение по основанию 2 делит вы- борку N × N элементов на четыре выборки
NN
--X--
элементов и т. д. до тех пор, пока не останутся выборки 2 × 2 элементов (см. рисунок).
Алгоритм двумерного ДПФ с разбиением на строки и столбцы требует проведения 2N-одномерных ДПФ, и вычислительная сложность его составляет N2 log2 N комплексных умножений и 2 ■ N2 log2 N комплексных сложений.
Разработка различных модификаций алгоритма Кули–Тьюки в одномерном и многомерном случаях проводилась М. В. Носковым, А. В. Старовойтовым и другими исследователями в работах [10–13]. Все результаты работ направлены на уменьшение времени вычислений. Этого можно добиться путем уменьшения числа операций комплексного умножения и сложения, изменения основания алгоритма Кули–Тьюки или распараллеливая вычисления. Кроме того, само комплексное умножение можно вычислять различным образом – через 4 действительных умножения и 2 сложения или за 3 действительных умножения и 3 действительных сложения.
Рассмотрим сигнал f , который является периодическим сигналом с периодом p ∙ 2 s (см., например, [14]). Отсчеты задаются как fk где k = 0, 1, ^ , p ■ 2 s - 1. Дискретное преобразование Фурье для данного сигнала f задается формулой
вит p ■ 2 ' ■ s комплексных сложений и p ■ 2 ' ■ 2 ком-
p -2 s -1
F(t) = I fke k=0
2 л i kt
> P "2
.
Разобьем данную сумму на 2 s сумм следующего вида
2 s -1 p - 1 -2^ t ( pk 1 + k 2 )
F (t) =II fpkx+ k 2 ep" s ki =0 k 2 =0
2 s -1
p -1
= I I fPM k 2 e
k 1 =0
k 2 =0
2 л i tk2 . p '2 s
2 n i , tk 1
e 2 s .
Внешнюю сумму можно рассматривать как преобразование Фурье для сигнала с числом отсчетов 2 s , для подсчета которого можно воспользоваться алгоритмом Кули–Тьюки, а внутреннюю сумму вычислить как ДПФ для сигнала с числом отсчетов р . Тогда общее число операций в полученном алгоритме соста-
плексных умножений.
Модифицированный одномерный алгоритм БПФ по аналогу Кули–Тьюки в MATLAB. Описанный алгоритм был реализован в виде программы в системе компьютерной математики MATLAB и протестирован на наборе, состоящем из 16384 отсчетов сигнала. Время выполнения программы сравнивалось со временем, потраченным на вычисление ДПФ с помощью встроенного алгоритма среды MATLAB. В таблице приведены данные выполнения модифицированного алгоритма и встроенной версии, программа тестировалась на виртуальной машине со следующими параметрами: AMD Phenom X2 3.2GHz, 2 Gb ОЗУ. Время выполнения сократилось в среднем на 20 %. Разработанная программа была зарегистрирована [15].
Заключение. Представлена реализация модифицированного алгоритма по аналогу Кули–Тьюки дискретного преобразования Фурье для одномерного сигнала с числом отсчетов p ∙ 2 s . Для данного алгоритма была разработана программа в системе компьютерной математики MATLAB. Авторы ставили перед собой задачу реализации модифицированного одномерного алгоритма БПФ по аналогу Кули–Тьюки именно в MATLAB, так как для реализации цифровой обработки сигналов радиоприемных устройств на практике часто используют программное обеспечение фирмы Xilinx (LogiCORE IP Fast Fourier Transform), где БПФ реализовано по алгоритму Кули–Тьюки в MATLAB.
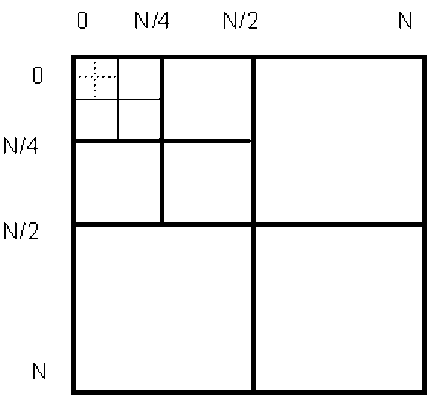
Схема прореживания двумерного ДПФ по основанию 2
Время выполнения модифицированного алгоритма и встроенного алгоритма Кули–Тьюки в MATLAB
|
Модифицированный алгоритм |
Встроенный алгоритм |
|
2,063 |
2,634 |
|
2,004 |
2,523 |
|
2,025 |
2,484 |
|
2,013 |
2,582 |
|
2,053 |
2,404 |
|
1,996 |
2,353 |
|
2,014 |
2,634 |
Дальнейшую перспективу работы авторы статьи видят в проведении сравнительного анализа разработанного алгоритма в среде MATLAB с другими алгоритмами, описанными в недавних работах современных исследователей.
Acknowledgments. The second author was supported by grant of the Ministry of Education and Science of the Russian Federation № 1.1462.2014/K.
Список литературы О модификации быстрого одномерного преобразования Фурье по алгоритму Кули-Тьюки
- Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. М.: Мир, 1988. 488 c.
- Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. М.: Мир, 1989. 448 c.
- Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов. М.: Связь, 1979. 416 с.
- Гонсалес Р., Вудс Р. Цифровая обработка изображений. М.: Техносфера, 2005. 1072 с.
- Cooley J. W., Tukey J. An algorithm for the machine calculation of complex Fourier series//Math. Comput. 1965. Vol. 19, No. 90. P. 297-301.
- Rudnick P. Note on the calculation of fourier series//Math. Comp. 1966. Vol. 20, No. 3. P. 429-430.
- Danielson G. C., Lanczos C. Some improvements in practical fourier analysis and their application to x-ray scattering from liquids//J. Franklin Inst. 1942. Vol. 233, No. 4. P. 365-380.
- Heideman M. T., Johnson D. H., Burrus C. S. Gauss and the history of the fast fourier transform//The ASSP Magazine. 1984. Vol. 1, No. 4. P. 14-21.
- Cooley J. W., Lewis P. A., Welch P. D. An algorithm for the machine calculation of complex fourier series//IEEE Trans. Audio Electroacoustics. 1967. Vol. 15, No. 2. P. 76-79.
- Старовойтов А. В. О многомерном аналоге алгоритма Кули-Тьюки//Вестник СибГАУ. 2010. Т. 27, № 1. С. 69-73.
- Киселев О. И., Кольцова И. В., Тутатчиков В. С. Схема параллельного вычисления одномерного быстрого преобразования Фурье//Наука и образование в XXI веке: материалы Междунар. науч.-практ. конф. (30 сент. 2013, г. Тамбов): в 8 ч./Институт повышения квалификации. Тамбов, 2013. С. 140-141.
- Tutatchikov V. S., Kiselev O. I., Noskov M. V. Calculating the n-Dimensional Fast Fourier Transform//Pattern Recognition and Image Analysis. 2013. Vol. 23, No. 3. P. 429-433.
- Noskov M. V., Tutatchikov V. S. Modification of a two-dimensional fast fourier transform algorithm for a rectangle signal//Pattern Recognition and Image Analysis. 2015. Vol. 25, No. 1. P. 81-83.
- Малоземов В. П., Машарский С. М. Основы дискретного гармонического анализа. СПб.: НИИММ, 2003.304 c.
- Программа для вычисления одномерного быстрого преобразования Фурье на основе модифицированного алгоритма Кули-Тьюки: свидетельство о гос. регистрации программы для ЭВМ/Т. В. Сидорова, Т. В. Зыкова; Роспатент. № 2014661701 РФ; заявл. 19.09.2014 (заявка № 2014619428); зарег. 11.11.2014.
- Dadzhion D., Mersero R. Tsifrovaya obrabotka mnogomernykh signalov . Moscow, Mir Publ., 1988, 488 p.
- Bleynut R. Bystrye algoritmy tsifrovoi obrabotki signalov . Moscow, Mir Publ., 1989, 448 p.
- Oppengeym A. V., Shafer R. V. Tsifrovaya obrabotka signalov . Moscow, Svyaz Publ., 1979, 416 p.
- Gonsalez R., Woods R. Tsifrovaya obrabotka izobrazhenii . Moscow, Tehnosfera Publ., 2005, 1072 p.
- Cooley J. W., Tukey J. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, Vol. 19, No. 90, P. 297-301.
- Rudnick P. Note on the calculation of fourier series. Math. Comp. 1966, Vol. 20, No. 3, P. 429-430.
- Danielson G. C., Lanczos C. Some improvements in practical fourier analysis and their application to x-ray scattering from liquids. J. Franklin Inst. 1942, Vol. 233, No. 4, P. 365-80.
- Heideman M. T., Johnson D. H., Burrus C. S. Gauss and the history of the fast fourier transform. The ASSP Magazine. 1984, Vol. 1, No. 4, P. 14-21.
- Cooley J. W., Lewis P. A., Welch P. D. An algorithm for the machine calculation of complex fourier series. IEEE Trans. Audio Electroacoustics. 1967, Vol. 15, No. 2, P. 76-79.
- Starovoitov A. V. . Vestnik SibGAU. 2010, No. 1 (27), P. 69-73 (In Russ.).
- Kiselev O. I., Kolthova I. V., Tutatchikov V. S. . Мaterialy XV Mezhdunar. nauch. konf.
- “Nauka i obrazovanie v XXI veke” . Tambov, 2013, P. 140-141 (In Russ.).
- Tutatchikov V. S., Kiselev O. I., Noskov M. V. Calculating the n-Dimensional Fast Fourier Transform. Pattern Recognition and Image Analysis. 2013, Vol. 23, No. 3, P. 429-433.
- Noskov M. V., Tutatchikov V. S. Modification of a two-dimensional fast fourier transform algorithm for a rectangle signal. Pattern
- Recognition and Image Analysis. 2015, Vol. 25, No. 1, P. 81-83.
- Malozemov V. P., Masharsky S. M. Osnovy diskretnogo garmonicheskogo analiza . St. Peterburg, NIIMM Publ., 2003, 304 p.
- Sidorova T. V., Zykova T. V. Programma dlya vychisleniya odnomernogo bystrogo preobrazovaniya Fur'e na osnove modifitsirovannogo algoritma Kuli-T'yuki . Certificate on the state registration of the computer program No. 2014661701 of the Russian Federation, dem. 19.09.2014 (demand No. 2014619428), registration 11.11.2014 Rospatent.


