О модификации декодера bit-flipping кодов с низкой плотностью проверок на четность

Введение . В 1963 году в работе [1] Р. Галлагер впервые описал класс линейных блочных кодов, проверочная матрица которых содержит малое количество ненулевых элементов. Такие коды принято называть кодами с низкой плотностью проверок на четность или LDPC-кодами (от англ. low-density parity check codes). Для них возможно построение кодеров и декодеров с невысокой вычислительной сложностью. Таким образом, при использовании LDPC-кодов скорость передачи данных существенно не ограничивается. Многие современные работы посвящены LDPC-кодам и их декодерам [2–5]. LDPC-коды активно используются в разных стандартах цифровой связи, например вай-фай (англ. Wi-Fi), 5G и оптической связи [6, 7]. Однако, несмотря на популярность этих кодов, некоторые связанные с ними задачи требуют исследования и решения. Одна из них — построение новых и улучшение существующих декодеров.

Цель данной работы — повышение корректирующей способности известного декодера bit-flipping LDPC-кодов (далее BF-декодер). Для этого строится модификация декодера, позволяющая динамически управлять одним из его основных параметров, выбор которого существенно влияет на качество декодирования.

Материалы и методы. Основными параметрами двоичных LDPC-кодов являются длина N, размерность К и минимальное расстояние кода d. Информационные слова [N, К, d]-кода С — это векторы т = (m₁,m₂, ...,т_к) Е F ^ , где F 2 — поле Галуа мощности 2, а кодовые слова — векторы с = (с 1 ,с₂, ...,c_v) Е F 2^v [8]. Удобно задавать LDPC-коды проверочной (N — К) х N матрицей Н. Большее количество ее элементов — нулевые [1], поэтому удобнее хранить ее не целиком, а запоминая только позиции ненулевых элементов по строкам.

Различают регулярные [9] и нерегулярные [10] LDPC-коды. В регулярных кодах все строки и столбцы проверочных матриц содержат фиксированное количество единичных элементов (к и j соответственно), иначе

Информатика, вычислительная техника и управление

код называют нерегулярным. Для удобства проверочные матрицы регулярных LDPC-кодов будем называть регулярными матрицами, а нерегулярных LDPC-кодов — нерегулярными.

Регулярные LDPC-коды обладают рядом преимуществ: легко оцениваемые параметры кода, удобство хранения матриц, невысокая вычислительная сложность алгоритмов кодирования и декодирования и пр. Кроме этого, декодеры регулярных кодов исправляют ошибки равномерно, в отличие от нерегулярных, которые исправляют ошибки в некоторых частях кодового слова хуже, чем в других. Однако задача генерации регулярных матриц с заданными свойствами является сложной, часто для ее решения используются методы перебора.

Для обсуждения свойств матрицы Н удобно использовать соответствующий ей граф Таннера G = (V, Е"), где Е — множество ребер, а V = SUR — множество вершин, 5 — множество строк матрицы Н, а R — множество ее столбцов [11]. Каждый ненулевой элемент Н, стоящий в i -й строке и j -м столбце, задает ребро, соединяющее -ю вершину множества S и j-ю вершину множества R. На рис. 1 представлен пример регулярной проверочной матрицы 3 x 6 c параметрами к = 4 и j = 2 и соответствующий ей граф Таннера.

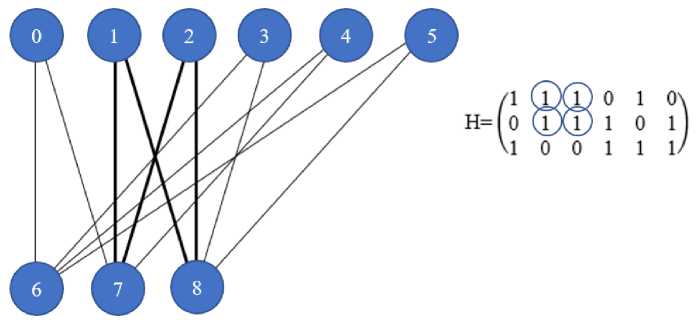
Рис. 1. Цикл в графе Таннера и в проверочной матрице

Верхний ряд вершин графа соответствует столбцам матрицы Н, а нижний ряд связан со строками Н. Важная характеристика проверочной матрицы Н LDPC-кода — наличие и тип циклов в соответствующем ей графе Таннера. Цикл — это такая последовательность смежных вершин графа, в которой первая и последняя вершины совпадают. Длина этой последовательности называется длиной цикла. Минимальная длина цикла в графе называется обхватом. Если граф не содержит циклов, его обхват полагают бесконечным. Пример цикла длины 4 выделен жирными линиями на графе (рис. 1).

Возможности по исправлению ошибок зависят не только от основных параметров LDPC-кодов, но и от структуры проверочной матрицы Н. С одной стороны, наличие циклов небольших длин (таких как 4 и 6) заметно ухудшает корректирующую способность декодера [12]. С другой стороны, код, которому соответствует граф Таннера без циклов, не исправляет ошибок, т. к. его минимальное кодовое расстояние равно 2. Таким образом, задача построения проверочных матриц регулярных LDPC-кодов является многопараметрической. При ее решении необходимо следить за основными параметрами кода, а также за циклами в графе Таннера, соответствующем проверочной матрице.

Рассмотрим в удобном виде известный BF-декодер LDPC-кода С [13].

Вход: LDPC-код С с параметрами [W, К, d], заданный проверочной матрицей

Н=(

\ h

h 11	h 12	h1N
h 21	h 22	h2N
■ (N-K)1	h(N-K)2	..  h( N -KjN

)

Вектор с' = с + е, с Е С(с F-jj, е (Е F2j — вектор ошибок; р — количество итераций алгоритма; T — пороговое значение.

Выход: кодовый вектор с Е С(с F ^ j.

Шаг 1. Положим счетчик г равным нулю.

Шаг 2. Вычислим синдром s = с'Н^т . Если s = 0 или г = р, то переходим на шаг 5.

Шаг3. Выделим из вектора s = (s 1 ,s₂, —,s_N-Kj единичные координаты, т. е. s , = 1, i = 1,(N — К).

Составим множество L = {i|s, = 1}. Вычислим h' = (h1,h-, .^,h'Nj, где h‘ = ^ieLhu.                                                    (2)

Величины h_u , I = 1, ^,N следует полагать неотрицательными целыми числами. Таким образом, К ' Е N q , где N₀ = N U {0}.

Шаг 4. В векторе К ' = (К ' , К '2 , .„,h'_N') находим все элементы К ' >  Т. Среди них выбираем случайный К ' и инвертируем бит с ' вектора с. Добавляем к счетчику г единицу и переходим на шаг 2.

Шаг 5. с = с ' .

Исследования, проведенные в рамках данной работы, позволяют сделать ряд замечаний по BF-декодеру.

Замечание 1. Входной параметр р задает максимальное количество итераций алгоритма со 2-го по 4-й шаги, но декодер может восстановить кодовое слово за меньшее число итераций.

Замечание 2 . При выборе параметра Т нужно руководствоваться следующими соображениями. Если известен параметр d используемого [N,K, d]-кода С, то по нему можно вычислить t — число гарантированно исправляемых ошибок, и тогда количество итераций декодера ограничивается этим значением:

P = t = 1 ^=1 ].                                                 (3)

Здесь [xj — округление числа х до меньшего целого. Если параметр d неизвестен, то его можно оценить с помощью границы Синглтона [5]

d

и, используя (3), получить р=т

Замечание 3. Структура декодера такова, что восстановление корректного кодового слова не гарантируется, даже если в зашумленном слове с' = с + е возникло не более t ошибок (3).

Замечание 4. В литературе для регулярных проверочных матриц в BF-декодере рекомендуется выбирать порог Т зависящим от веса j столбца матрицы Н, а именно Т = ^ . Для нерегулярных матриц такие рекомендации в литературе не приведены. Корректирующую способность BF-декодера может ухудшить неудачный выбор порога Т. При его большом значении на шаге 4 декодера в векторе К ' может не найтись координаты, превосходящей порог Т, следовательно, не будут исправлены ошибочные биты. При выборе малого значения Т на шаге 4 BF-декодера в векторе К ' может появиться несколько координат, значение которых превышает порог. Среди них могут быть и координаты, не содержащие ошибку. Таким образом, выбор параметра T может в значительной мере повлиять на качество декодирования.

Результаты исследования. Сформулируем и докажем лемму о максимально возможном значении порога Т. Затем модифицируем BF-декодер таким образом, чтобы порог устанавливался в процессе декодирования динамически, и проведем сравнительный анализ оригинального и модифицированного алгоритмов декодирования.

Лемма . Пусть двоичный [N,K, d]-код С задан с помощью проверочной матрицы Н, имеющей фиксированное количество j единичных элементов в каждом столбце. Тогда максимальное значение порога Т для BF-декодера такого LDPC-кода С не может быть больше

Т = j - 1.                                                 (4)

Доказательство. Пусть из канала передачи получен вектор с’ = с + е, где с Е С — верное кодовое слово, е Е F 2 — вектор ошибок с весом Хэмминга и/(ё). Если w(e) = 0, то на шаге 2 вектор-синдром s = 0. Следовательно, алгоритм перейдет на шаг 5 и вернет с ' в качестве ответа. В этом случае значение порога не используется. Если и/(ё) > 0, то из регулярности Н вытекает справедливость неравенства К ' <  j, где К' — элементы вектора К ' . Инвертирование бит с₁ вектора с ' происходит в алгоритме, только если К ' > Т. Следовательно,

Т <  К ' <  j.

Таким образом, формула (4) верна.

Внесем в BF-декодер изменения, которые позволят определять величину порога динамически, в зависимости от степени повреждения кодового вектора в канале передачи.

Информатика, вычислительная техника и управление

Вход: [N,K,d]-код С, заданный приведенной выше проверочной матрицей (1). Вектор с ' = с + ё, где сЕС(с F2^V), ё (Е F^") — вектор ошибок; р — количество итераций алгоритма; Т — некоторое пороговое значение, выбранное заранее.

Выход: кодовый вектор сЕС(с F^y

Шаг 1. Положим счетчик г равным нулю.

Шаг 2. Вычислим синдром s = с ' Н^т. Если s = (0, ... ,0) или г = р, то переходим на шаг 7.

Шаг 3. Выделим из вектора s = (s₁,s₂,.,s_N-K‘) единичные координаты, т. е. s , = 1, i = 1, (N —К). Составим множество L = {i|s , = 1}. Вычислим К ' = (К 1 ,К 2 , .,К у ), где К ' такой же, как и в оригинальном декодере (2). При суммировании величины К , _; 1 = 1, .,N, следует полагать неотрицательными целыми числами. Таким образом, К ' Е Ы у , где М₀ = М U {0}.

Шаг 4. Инициализируем значение порога Т = max(h ' )_i = _{1 N} — 1.

Шаг 5. Если Т > 0

Выберем произвольный элемент К ' вектора К ' — такой, что К ^ >  Т.

Инвертируем бит с ^ .

Шаг 6. Добавим к счетчику г единицу и перейдем на шаг 2.

Шаг 7. с = с ' .

Замечание 5. Модифицированный алгоритм в целом выполняет меньше итераций, чем BF-декодер, т. к. на шаге 4 порог выбирается динамически. Следовательно, декодер не выполняет бесполезные итерации, на которых не изменяются биты вектора с ' . Значение порога в модифицированном декодере зависит от числа ошибок, повредивших кодовое слово, и сразу устанавливается таким, что в зашумленное кодовое слово с'

гарантированно вносятся изменения.

Оценим сверху количество операций сложения, сравнения и присваивания в обоих декодерах. В оригинальном BF-декодере [N,K,d]-кода С производится р(кК + (N — K)М + 1) операций сложения, p(3N — 2К + 2) операций сравнения и p((N — К)(к + 1) + 2N + 3) + 1 операций присваивания. В BF-декодере с динамическим порогом — р(кК + (N — K)М + 3) операций сложения, p(5N — 2К + 3) операций сравнения и p((N — К)(к + 1) + 2N + 4) + 1 операций присваивания. Здесь р — параметр декодера, устанавливающий максимальное количество операций, к — вес строк проверочной матрицы кода. Заметим, что при реализации алгоритма фактически не используются операции умножения и деления, т. к. на втором шаге для вычисления синдрома s удобно использовать операции сложения вместо умножения. Напомним, что матрица Н обладает разреженной структурой, и ее строки удобно хранить в виде списка номеров ненулевых элементов. Следовательно, вместо умножения вектора с' на матрицу Н необходимо суммировать координаты вектора с' , номера которых совпадают с номерами ненулевых элементов в соответствующей строке матрицы Н.

В сравнении с оригинальным алгоритмом модифицированный BF-декодер выполняет больше операций, но не значительно: число операций сравнения увеличилось на p(2N + 1), присваивания — на р, сложения — на 2р.

Для сравнительного исследования корректирующей способности оригинального и модифицированного алгоритмов декодирования создано программное средство, реализующее имитационную модель двоичного симметричного идеально синхронизированного помехоустойчивого канала связи согласно [14–16]. Для обеспечения помехоустойчивости в модели использованы LDPC-коды и BF-декодеры (оригинальный и с динамическим порогом). Ошибки в канале моделировались независимыми и равномерно распределенными.

В экспериментах использованы специально найденные проверочные матрицы, задающие LDPC-коды. Опишем основные параметры этих матриц, используя стандартные обозначения основных параметров кода, а также: j и к — вес каждого столбца и вес каждой строки проверочной матрицы соответственно; ю₄, ю₆ — 4 и 6 циклов в графе Таннера, соответствующем проверочной матрице.

Регулярная матрица Н1: N = 20, К = 5, j = 3, к = 4, d = 6, ю4 = 0, ю6 =41

Регулярная матрица Н2: N = 28, К = 7, j = 3, к = 4, d = 6, ю4 = 0, ю6 =42

Регулярная матрица Н3: N = 28, К = 7, j = 3, к = 4, d = 6, ю4 = 0, ю6 =29

Нерегулярная матрица Н4: N = 32, К = 5, j = 3, d = 12, ю4 = 0, ю6 =0

С использованием этих матриц были построены кодеки LDPC-кодов и проведены имитационные эксперименты. На рис. 2–5 представлены графики зависимости корректирующей способности построенных кодеков LDPC-кодов от вероятности ошибки в канале. Обоснование выбора значений порога Т = 1 и Т = 2 в BF-декодере см. в замечаниях 3, 4 и лемме.

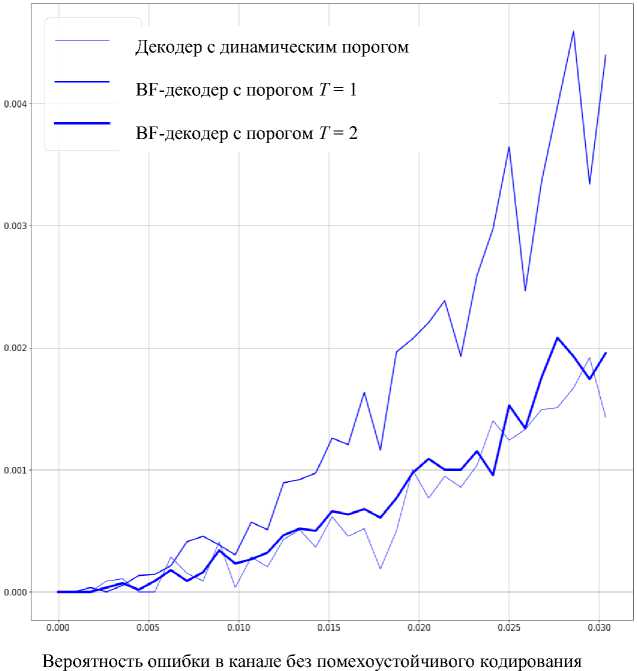
Рис. 2. График корректирующей способности декодеровдля LDPC-кодов, заданных матрицей Н ₂

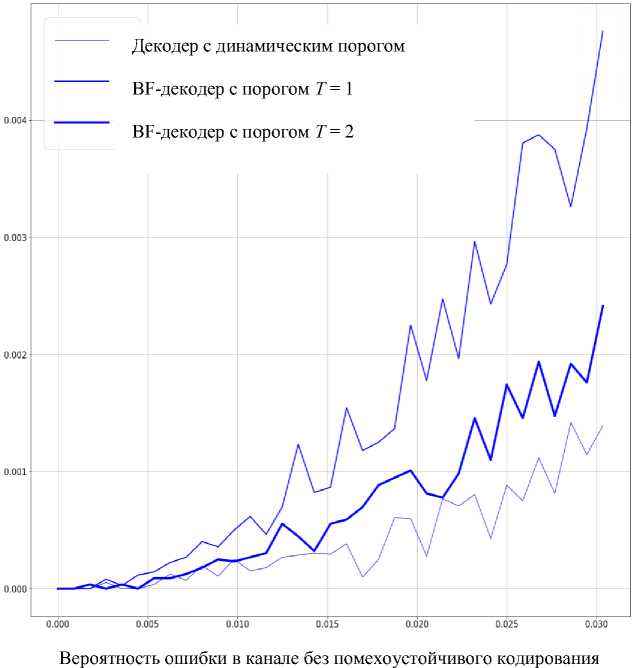
Рис. 3. График корректирующей способности декодеров для LDPC-кодов, заданных матрицей Н ₃

Информатика, вычислительная техника и управление

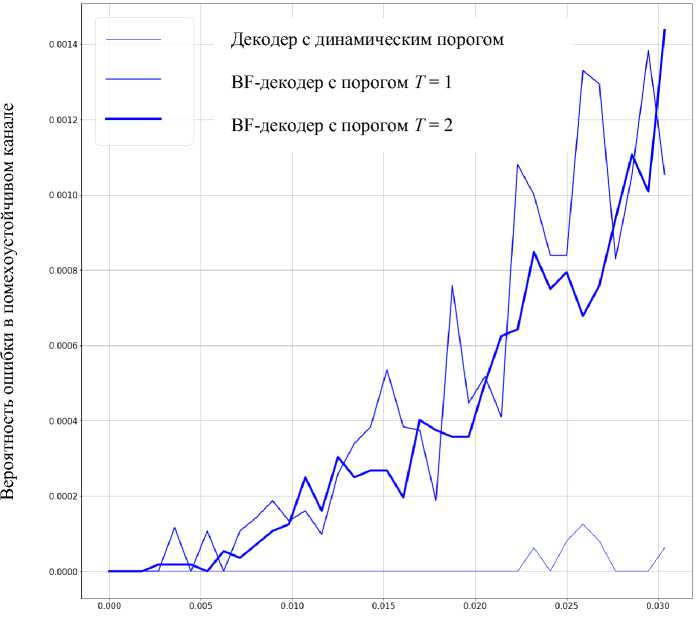
Вероятность ошибки в канале без помехоустойчивого кодирования

Рис. 4. График корректирующей способности декодеров для LDPC-кодов, заданных матрицей Н ₄

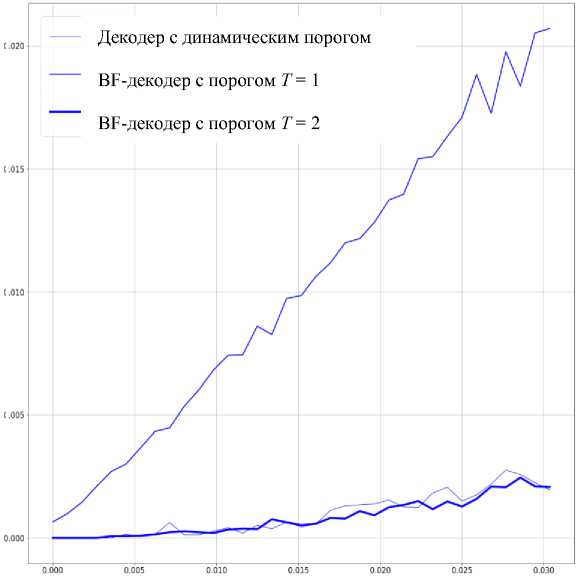
Декодер с динамическим порогом

BF-декодер с порогом T = 2

BF-декодер с порогом T = 1

Вероятность ошибки в канале без помехоустойчивого кодирования

Рис. 5. График корректирующей способности декодеров для LDPC-кодов, заданных матрицей Н 1

В диапазоне реального уровня ошибок [8, 13, 14] на рис. 2–4 можно наблюдать, что BF-декодер при значении порога Т = 2 показывает лучшие результаты, чем при Т = 1, а модифицированный BF-декодер обладает лучшей корректирующей способностью по сравнению с оригинальным.

Декодеры демонстрируют схожую эффективность при малых значениях длины кода, однако при ее увеличении модифицированный декодер показывает лучшие результаты. Так, при вероятности ошибки в непомехоустойчивом канале 0,05 различие в вероятности ошибки в помехоустойчивом канале при использовании BF-декодера с порогом Т = 2 и Т = 1 составляет от 0,005 до 0,03 в пользу использования большего значения порога. Если же задействовать BF-декодер с порогом Т = 2 и модифицированный декодер, это различие колеблется в зависимости от LDPC-кода в интервале от 0,001 до 0,003. При вероятности ошибки в непомехоустойчивом канале 0,1 вероятность ошибки в помехоустойчивом канале при использовании BF-декодера с порогом Т = 2 меньше, чем с порогом Т = 1, на величину от 0,001 до 0,02. При использовании BF-декодера с порогом Т = 2 и модифицированного декодера это различие колеблется в зависимости от LDPC-кода в интервале от 0,002 до 0,01.

Оба декодера чувствительны к количеству циклов в графе Таннера, соответствующему проверочной матрице LDPC-кода. Чем больше отношение количества циклов к общему количеству элементов в матрице, тем хуже исправляет ошибки любой BF-декодер. При проведении экспериментов было интересно выяснить, можно ли так увеличить количество циклов в матрице, что модифицированный декодер покажет худшие результаты по сравнению с BF-декодером. Опытным путем была найдена такая матрица — Н 1 , содержащая 41 цикл длины 6. Результаты исследования корректирующей способности декодеров для этой матрицы показаны на рис. 5. Заметим, однако, что матрица Н₂ содержит еще больше циклов длины 6, а именно 42. Принципиальное отличие матриц Н 1 и Н₂ — в плотности единиц:

— в Н 1 — 60 единичных элементов на 300 элементов матрицы,

— в Н2 — 84 единицы на 588 элементов матрицы.

Напомним, что особенностью LDPC-кодов является разреженная структура проверочной матрицы, поэтому Н2 более типична для LDPC-кодов.

Обсуждение и заключения . В работе рассмотрен декодер bit-flipping двоичных LDPC-кодов. Даны рекомендации о выборе таких входных параметров декодера, как порог и количество итераций алгоритма. Сформулирована и доказана лемма о максимальном значении порога декодера. Разработана модификация BF-декодера двоичных LDPC-кодов, в которой предлагается задавать порог динамически во время выполнения алгоритма в зависимости от полученного синдрома. Для оригинального и модифицированного декодеров найдены верхние оценки количества операций. Эти оценки показывают, что модификация усложняет декодер незначительно. Проведенные имитационные эксперименты демонстрируют лучшую корректирующую способность модифицированного декодера по отношению к оригинальному. Эксперименты также показали зависимость качества декодирования от степени разреженности матрицы и количества циклов длины 6 в графе Таннера, соответствующего проверочной матрице LDPC-кода. Таким образом, возникает задача построения проверочных матриц с малым количеством коротких циклов, что является предметом дальнейших исследований.