О модификациях метода построения линейной дискриминантной функции, основанного на процедуре Петерсона-Маттсона

Процедура вычисления параметров линейной дискриминантной функции d(x) , минимизирующей величину общего риска, была предложена D. Peterson и R. Mattson в работе [1] и описана также в монографии [2]. Эта процедура разрабатывалась в предположении, что значения дискриминантной функции имеют нормальный закон распределения в каждом из классов. Кроме того, известная процедура нахождения параметров имеет ряд ограничений для достаточно типичных на практике ситуаций, например, когда средние признаков в классах близки или совпадают. Данная работа расширяет область применения известного метода построения дискриминантной функции за счет модификации процедуры Петерсона-Маттсона.

Работа организована следующим образом. Метод построения линейной дискриминантной функции, основанный на известной процедуре Петерсона-Маттсона, представлен в первом разделе. Во втором разделе будет доказано, что известная процедура дает решение не только для задачи минимума общего риска (линейной оптимизации), но также и для задачи Неймана-Пирсона построения линейной дискриминантной функции. Некоторые замечания о диапазоне параметра, используемого в процедуре Петерсона-Матсона, будут сделаны в третьем разделе. Будет показано, что ограничения, налагаемые на область значений параметра в известной процедуре, не являются корректными. Будут указаны корректные границы для этого параметра, а также достаточные условия, при которых известные границы являются корректными. Наконец, в четвертом и пятом разделах будет предложена процедура получения параметров линейной дискриминантной функции для ситуации, когда математические ожидания вектора признаков, вычисленные для различных классов совпадают.

1. Метод построения линейной дискриминантной функции, основанный на процедуре Петерсона-Маттсона

Пусть линейная дискриминантная функция (ЛДФ) d ( x ) = W T x + w_w имеет нормальный закон распределения в каждом из классов. Это может быть обусловлено следующими причинами:

• •    если вектор признаков X имеет нормальный за-

• кон распределения в каждом из классов, тогда линейная комбинация элементов вектора также имеет нормальный закон распределения;

• •    если вектор признаков X не имеет нормальный

закон распределения, но количество признаков достаточно большое, тогда (при достаточно общих условиях) в силу центральной предельной теоремы линейная комбинация элементов этого вектора также имеет нормальный закон распределения.

При выполнении указанного допущения поведение случайных значений функции d (X) в каждом из классов полностью характеризуется математическим ожиданием и дисперсией этой функции в каждом из классов, а именно:

m = M Г d ⁽ X V )

i

V / ^Q i) а 2 = D Г d ⁽ X Ю i

V / ^Q i)

= W T M i + к , ,

= W T B i W ,   i = { 0,1 }.

Здесь M_i , B_i – это вектор математических ожиданий и ковариационная матрица вектора признаков в классе Q i , соответственно.

Пусть дискриминантная функция строится из условия минимума общего риска классификации (по параметрам дискриминантной функции):

R min = Г о P ( Q /Qo ) + Г 1 P ( Q М ) ^ min , (2)

W,wN где событие Q = {d(X)> 0}. С учетом того, что дискриминантная функция имеет нормальный закон распределения, данный критерий эквивалентен следующему:

^m 0/^a0

s = —,        0,   , a = ^m 1 /^{g2 -} m 0/^G0 .

^m 1 /^a2 ^- m 0/^a 0

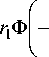
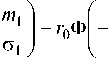
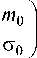
^ min . W , w N

Тогда для порогового значения дискриминантной функции можно получить следующее выраже-ниея:

Здесь ф ( - ) - функция Лапласа. Необходимым

_ s ^G 0 ^MT ^{+( 1 -} s ^)a 2 ^M Try w^N = s a ₀ + ( 1 - s ) a 2     ^{W .}

условием минимума, как известно, является равенство нулю производной критерия:

f miI          mo I п г1Ф11 I - г0Ф'|0 I = 0 .

V ^G l J       V ^G 0 J

Тогда, учитывая, что выполняются равенства [1, 2]

d Г mi | = Mi W TBm, dWl a, J a, a3

i(3)

°  -i^-    — z=01

, dwN ( a i Ja

получим систему уравнений:

r ₀

V2 na ₀

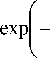
^m 0²

^{2 a} 0

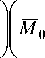
^{m 0} W^TB 0 ^a 0

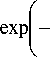
^m 1²

2a2

r ₁

T2 na ₁

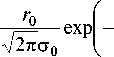
m t^{1 2 a} 0 J

M 1

m WTB1 I, a2 J

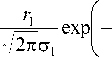
^m 1²

2a2

Из этой системы уравнений очевидно следующее равенство:

M 0 - m 0 W T B 0 = M i - mW T B i .

^a 0                 ^a 2

или

f m B l - m B 0 W = M 1 - M 0 .           (5)

l^a 2       ^a 0 J

Явного выражения для решения такого соотношения получить не удается, поскольку величины m i , a ² ( i = 0,1 ) , задаваемые соотношениями (1), зависят от вектора коэффициентов W линейной дискриминантной функции.

Для численного решения выражения (5) D. Peterson и R. Mattson в 1966 году предложили подход, позволяющий свести решение системы нелинейных уравнений (5) к итерационной поисковой процедуры, которая зависит от одного скалярного параметра. Предложенный ими подход состоит в следующем.

Вектор W определяется как функция некоторо-

го числового параметра s :

W = a [ sB 0 + ( 1 - s ) B 1 ]^{- 1} ( M 1 - M 0 ) ,             (6)

Оно может быть использовано для расчета w_N при известном векторе коэффициентов W линейной дискриминантной функции. Из этого выражения очевидно, что умножение вектора коэффициентов W на произвольное положительное число ведет к пропорциональному увеличению величины w_N . Таким образом, при расчете параметров классификатора произвольным положительным множителем у коэффициентов W линейной дискриминантной функции можно пренебречь, поскольку этот множитель меняет только «масштаб» значений дискриминантной функции, но не меняет классификацию.

Анализируя второе соотношение в системе уравнений (4), авторы предположили, что оптимальное решение приведет к тому, что величины m ₀ и m ₁ будут иметь разные знаки, то есть m ₀ <  0 , m 1 >  0 . В этом случае величина a в выражении (6) – это положительный масштабный множитель. В соответствие с ранее сделанными замечаниями этим масштабным множителем можно пренебречь.

Из предположения авторов о разных знаках средних дискриминантной функции в классах m ₀ <  0, m 1 >  0 также следует, что диапазон величины s е [ 0,1 ] . Тогда возможные значения коэффициентов W линейной дискриминантной функции задаются соотношением:

W = [ sB 0 + ( 1 - s ) B 1 ]^{- 1} ( M 0 - M 1 ), s е [ 0,1 ] . (9)

Окончательно значение параметров линейной дискриминантной функции определяется численно из решения оптимизационной задачи, в которой всего один независимый параметр оптимизации s :

г1ф|-ml I-г0ф|-m0 ]^min, (10) V a1 J v a0 J s а параметры линейной дискриминантной функции вычисляются в соответствие с выражениями (1), (8) и (9). Значение общего риска при таком подходе может также оцениваться по выборке.

Существует обобщение изложенного подхода для произвольного вида функционала качества [2], которое, однако, приводит только к системе уравнений и не дает окончательного решения. Одним из частных решений, полученных таким образом, является классификатор Фишера.

где

2. Определение параметров ЛДФ, оптимальной по критерию Неймана-Пирсона.

Другие критерии оптимальности

Во многих задачах вместо линейного критерия оптимизации используется критерий Неймана-Пирсона, который состоит в следующем. Фиксируется вероятность ложного обнаружения, и для этого фиксированного значения находятся такие параметры классификатора, которые минимизируют вероятность пропуска объекта. Таким образом, при построении ЛДФ, оптимальной по критерию Неймана-Пирсона решается следующая задача оптимизации:

'px ^ min, j       W, wN                                        (11)

I P о = P o .

Заметим, что различия в критериях Неймана-Пирсона и критерия минимума общего риска возникают только тогда, когда Паретто-оптимальное множество значений вероятностей ошибок ( p ₀ , p₁ ) имеет невыпуклый характер. Если множество значений вероятностей ошибок является выпуклым, то критерии Неймана-Пирсона и минимума риска эквивалентны при соответствующем выборе параметров критериев – величин r ₁ , r ₀ и p ₀ ^* [2]. В альтернативной ситуации линейная задача оптимизации не позволяет получить все решения на границе множества, а задача оптимизации по критерию Неймана-Пирсона позволяет это сделать.

Итак, пусть решается задача (11) для ЛДФ, и все описанные выше допущения на законы распределения значений ДФ справедливы. Тогда задача оптимизации может быть переписана с использованием метода множителей Лагранжа в виде следующей безусловной целевой функции вида:

P i + Ц⁽ P о - P 0 ) 2 ^ min ,

W ,wN здесь ц - множитель Лагранжа (ц>>0). Необходимое условие минимума запишется:

P ’ = 2 ц⁽ p 0 ^- p о ) p 0 -

Тогда если

P i = F d ⁽- m А 1 P 0 = 1 - F d ⁽- mT /^0 1 ,

V d i /    J              ( d 0 / J

получим следующее уравнение:

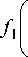
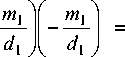
= 2 ц ^{1 -} P 0 V

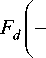
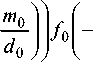
m ₀

-

m ₀

d

Подставляя в это равенство выражения для производных ( - mjdt ) по вектору коэффициентов ЛДФ W и порогу w_N из (3), снова приходим к аналогичной (4) системе уравнений:

1 _{f 0}

^ст 0

-

m ₀

ст 0

*

= 2 ц ^{1 -} P 0

V

M 0

V

-

F d

-

-

<

• M 1

-

V

¹ f 0

ст ₀

-

m ₀

ст ₀

*

= 2 ц ^{1 -} P 0

V

^m ₂ ⁰ W^TB 0 ст ₀

m ₀

d ₀

m 1 T

А

A

J

л

f 1

-

m ₁

•

J

^ст 1

^ст 1

"Г W T B 1 ,

ст ₁

-

F d

-

J

m ₀

d ₀

л

f ,

-

m ₁

.

J

ст ₁

ст ₁

Учитывая второе равенство, из первого соотношения получаем уравнение (5) относительно вектора W . Результатом рассуждений снова окажется итерационная процедура Петерсона-Матсона.

Тот факт, что, используя рассматриваемую процедуру, для любого значения вероятности ложной тревоги можно найти соответствующее ей наименьшее значение вероятности пропуска объекта означает, что процедура Петерсона-Матсона позволяет получить все Паретто-оптимальное множество решений. Следовательно, любую задачу построения ЛДФ с критерием, требующим совместного понижения значений вероятностей p ₀ и p ₁ , можно решить, используя процедуру Петерсона-Матсона – то есть простым перебором значений величины s . Этот факт очень удобен при построении ЛДФ на базе других критериев – нет необходимости разрабатывать для них новую процедуру поиска параметров ЛДФ.

3. Диапазон параметра оптимизации процедуры Петерсона-Матсона

В работах [1,2] диапазон параметра оптимизации s , определенного выражением (7), принимается следующим: ^ е [ 0,1 ] . Такое ограничение следовало из выполнения в системе уравнений (4) равенства

r» ⁽ m о I Г ⁽ m ² 0~р=^ exp l°- I = exp l^L- л/2 лст ₀ V 2 ст 0 J V2nCT ₁ V 2 ст ²

которое можно интерпретировать, как

r0

■75Пст0

exp

V

r1

'\/2Пст ₁

exp

( u - m ₀

2ст2

^u - m_x 2ст 2

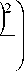
u =0

Последнее равенство имеет ясную геометрическую трактовку, представленную на рис. 1.

А именно, процедура Петерсона-Матсона так выбирает параметры ЛДФ, чтобы математические ожидания законов распределений различных классов располагались по разные стороны от начала ко-

ординат, причем их значения в начале координат совпадали. Тогда оптимальным пороговым значением, следующим также и из байесовской теории оптимизации, будет начало координат.

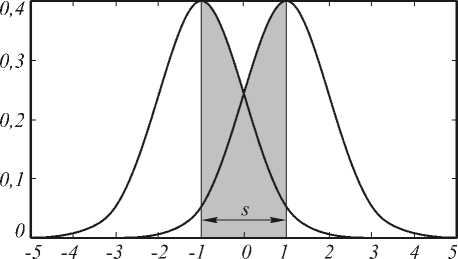
Рис. 1. Геометрическая интерпретация необходимого условия экстремума: ситуация высокой разделимости классов

В такой ситуации можно считать справедливым неравенство m 0 <  0 <  m 1 , и значение 5 действительно принадлежит вышеуказанному диапазону. На рис. 2 представлено изменение положения ДЛФ в двумерном пространстве признаков по мере изменения значения параметра.

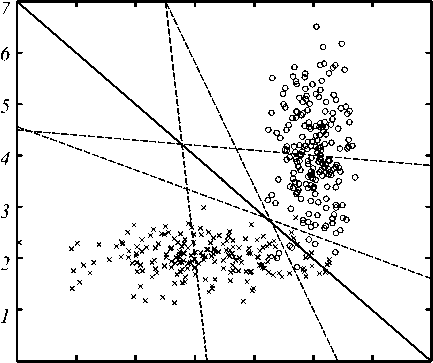
0       1    2     3     4     5     6    7

Рис. 2. Расположение ДЛФ, построенной с использование процедуры Петерсона-Маттсона для значений параметра s=0, 0.25, 0.5, 0.75 и 1

К сожалению, на практике часто возникают ситуации, когда классы плохо разделимы. Примеры таких ситуаций для одномерного и двумерного случаев приведены на рис. 3 и 4, соответственно. В частности, для одномерного случая, представленного на рис. 3, изменение параметра 5 в диапазоне [0,1] приведет к изме- нению реального порогового значения дискриминантной функции только в выделенном на рисунке отрезке. Очевидно, такое положение порогового значения не является оптимальным. В частности, байесовская теория оптимизации предполагает простановку границ в точках выполнения равенства:

Г f \ х/ | к f( х/ ) r 0 f I/O I = r l f I/O I '

V/ “ 0 7     V/ “ 1 7

Ситуация, приведенная на рис. 3 реально возникает, если, например, одно из весовых значений в целевой функции существенно больше другого, или если один из классов существенно больше «размыт» в признаковом пространстве, а также если средние векторов признаков в классах близки. А поскольку это достаточно реальные ситуации, то необходимо, оставаясь в рамках ЛДФ, уметь находить наилучшие решения. При этом заметим, что в этом случае возможно получения не одного, а нескольких локально- оптимальных решений, среди которых можно ото-

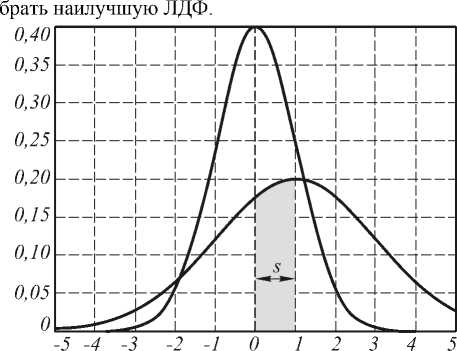
Рис. 3. Геометрическая интерпретация необходимого условия экстремума: ситуация низкой разделимости классов: M 0 =0, D 0 =1, M 1 =1, D 1 =4, r 0 =r 1

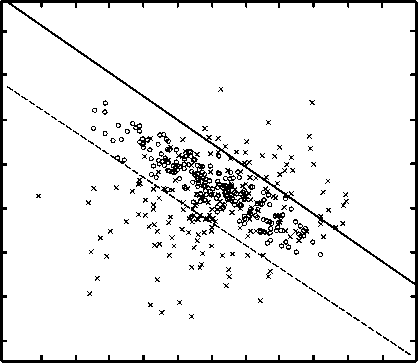
Рис. 4. Множество локальных решений ЛДФ, соответствующих параметру оптимизации s со значениями –0,024 и -0,094

Для обобщения известной процедуры необходимо расширить область параметра оптимизации s на все вещественную ось: 5 e R . На рис. 4 приведен пример для одной из таких ситуаций для двумерного вектора признаков и при близких значениях средних признаков в классах. Как видно, оптимальное значение параметра оптимизации выходит за границы [ 0,1 ] , используемые в известном методе.

Из графических иллюстраций, приведенных на рис. 1 и 3 легко видеть, что традиционные границы параметра оптимизации [0,1] справедливы лишь в той ситуации, когда максимальное значение плотности вероятностей, умноженной на соответствующее значение штрафа, одного класса больше значения плотности вероятностей, умноженной на соответствующее значение штрафа, другого класса при тех же аргументах. Таким образом, достаточное условие того, что известные границы параметра оптимизации 5 е [0,1] являются корректными представимо формально в виде системы неравенств:

r 0 c 0	>	r 1 с 1	exp	- l (
r 1		r 0
	>		exp	-
с 1		с 0		l

⁽ m 0 - m l ) 2 '

2 ^ 2    I

⁽ m о ^- m l ) 2 '

.

^{2 с} 0      I

^ 5 е [ 0,1 ] .

Следует отметить, что расширение границ значений параметра оптимизации решает проблему нахождения оптимальные значения ЛДФ для двух обозначенных выше ситуаций: когда одно из весовых значений в целевой функции существенно больше другого, и когда один из классов существенно больше «размыт» в признаковом пространстве. Для ситуации совпадающих средних данный подход не позволяет получить решения в силу однородности системы линейных уравнений (5). В этой ситуации, очевидно, следует использовать другой подход. Он изложен в следующем разделе.

• 4 . Построение ЛДФ

при совпадающих средних признаков в классах

Пусть средние векторов признаков в разных классах совпадают:

M 0 = M 1 = M .

Подставим это равенство в выражение (5), тогда последнее может быть переписано в виде:

mWTB0/с0 = mWT B1 Н , здесь m0 = m1 = m = W TM + wN . Перепишем его следующим образом:

( B 0/^ - B /с ? ) W = 0.                     (12)

Решить такое уравнения, также как и уравнение (5), аналитически невозможно. Поэтому введем, как в процедуре Петерсона-Матсона, переменную s:

• ⁵    = - (V ^с 0 ^- V с ² У1 А² = ^с 0/^{( с} 0 ^с 2 ) .

Тогда, с точностью до ненулевого масштабного множителя, условие (12) перепишется в виде однородной системы линейных уравнений, зависящей от параметра:

( 5B 1 + ( 1 - 5 ) B ₀ ) W = 0                          (13)

Заметим, что диапазон изменения переменной s, определяется всей числовой прямой 5 е R за исключением отрезка [0,1]. Кроме того, для конкретного значения s вектор W может не существовать.

Нетривиальное (ненулевое) решение однородной системы линейных уравнений существует тогда и только тогда, когда определитель матрицы

B £ = 5B 1 + ( 1 - 5 ) B 0 .                             (14)

оказывается нулевым det ( B £ ) = 0 . Тогда уравнение (13) относительно вектора W есть определение ортогонального векторного пространства к набору векторов-строк матрицы B £ . В свою очередь, матрица B £ есть результат взвешенной суммы ковариационных матриц векторов признаков в классах. Учитывая, что матрицы B 1 и B 0 невырожденные, условие (13) можно преобразовать к виду:

det ( B 1 B ₀ ^{- 1} + (( 1 - 5 )/ 5 ) ■ I ) = 0                     (15)

здесь I – единичная матрица. Значения величины ( 1 - 5 )/ 5 лежат на всей числовой оси, за исключением точки 5 = 0 . Но при этом значении определитель матрицы (14) отличен от нуля, так как B £ 0 = B ₀ . Поэтому можно переписать (15) в виде:

det ( B £ ) = 0, где B £ = B 1 B 0 ^{- 1} + 5I , 5 e R .     (16)

Далее, в задаче используется N признаков, а размер матрицы B 1 B ^{- 1} составляет N x N . Тогда можно переписать условие (16) в виде (степенного) уравнения N -ого порядка относительно величины s . Максимальное количество линейно независимых векторов-решений W уравнения (16) не превышает N , причем при одном значении переменной s (корне) число решений равно кратности корня. Сам же вектор W может легко быть найден с помощью процедуры Грамма-Шмидта ортогонализации набора векторов: строк матрицы (16) и некоторого произвольного вектора W . Окончательно вектор весовых коэффициентов ЛДФ W выбирается из множества локальных решений:

W e< W : B ~ £ 5 W = 0, где 5 = argdet ( B ~- £ ) = 0 ^ .

[                                  t E R

Пусть далее вектор W найден. Для получения окончательного ответа необходимо определить значение порогового значения w_N . В общем случае, когда распределение значений дискриминантной функции отлично от нормального (см. раздел 2), пороговое значение ЛДФ может легко быть найдено численными методами, например, по выборке. Для случая нормального закона распределения значений дискриминантной функции можно получить аналитическое выражение следующим образом. Это выражение следует из второго уравнения системы (5) при условии равных средних m ₀ = m 1 = m :

• r_n         |     m ² | r         |     m ² |

• 0-^ — exp l--- I = —^=1 — exp l--- I .

V2 ^пс 0    l ^{2 с} 0 J  V2^nc 1    ( 2 ^с 2 J

Преобразуя это выражение, имеем:

m = ±o ₀ o ₁

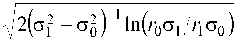
причем выполняются равенства ab >  c ² и de >  f ² . Тогда матрица B _£ :

Учитывая, что m = W T M + w_N , получим окончательное явное выражение для искомой пороговой величины ЛДФ:

W n =±^ 0 oJ- ----ln l ^ 0 ^ 1 I - W T M .      (17)

L о ^O o l по J

Следует отметить, что задача поиска оптимального значения порогового значения w_N неразрешима, если подкоренное выражение оказывается отрицательным. Это может произойти, если выполняется одно из следующих соотношений:

^O 1 > ^ и Г о ° 1 <  ^r i ° 0

или

^O 1 < ^ и r o O >  r i ^ o .

На рис. 5 представлена графическая интерпретация подобной ситуации, которая возникает, когда штрафы за решения выбраны таким образом, что минимум риска достигается только в ситуации, если все пространство классифицируется в какой-то один класс.

^B £

sa + (1 - s ) d sc + (1 - s ) f sc + (1 - s ) f sb + (1 - s ) e

Условие (13) существования ортогонального пространства преобразуется к виду:

( sa + (1 - s ) d )( sb + (1 - s ) e ) - ( sc + (1 - s ) f ) ² = 0 .

Используем обозначения

A = ⁽ a ^- d )( b ^- e ^)-( c ^{- f ) 2,} C = de ^{- f} 2 ,

B = ae + bd + 2 f ² - 2 cf - 2 de

Тогда можно записать решение уравнения (16):

s₁₂ = ( - B ± 4в ² - 4 AC )/2 A .

Параметр w N может быть определен из равенства (17).

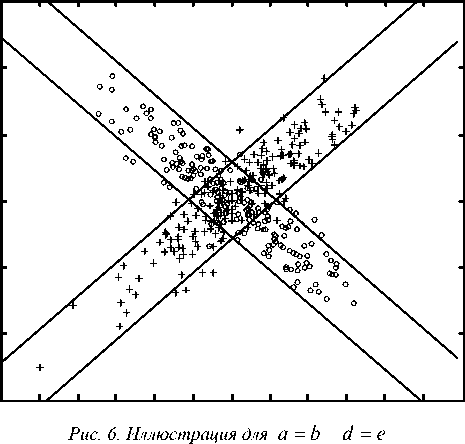
Наиболее простое решение получается в ситуации, когда дисперсии по координатам одинаковы, то есть a = b и d = e . Тогда:

B s ₁ =Y 1

1 1

, B L =Y 2

s ₂

^^^^^^B

^^^^^^B

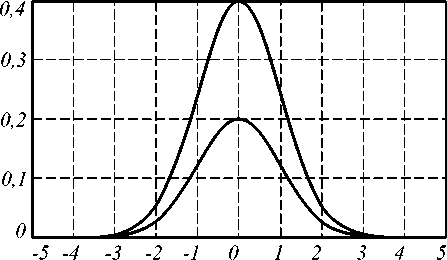
Рис. 5. Пример с отсутствием решения: M 0 = M 1 =0, D 0 =D 1 =1, r 0 =1, r 1 =0,5

А соответствующие векторы линейной дискриминантной функции, определяющие ортогональное подпространство, таковы:

W s1

-

1 ’

W s2

На рис.6 и 7 приведены примеры для двумерного

случая.

Подобная вырожденная ситуация невозможна, если риски за ошибки одинаковы и/или решение принимается на основе анализа только плотностей законов распределений. Единственная аномалия возникает, когда плотности совпадают, но тогда абсолютно бессмысленно выбирать какое-либо конкретное решение, так как все они дают одинаковую величину общего риска.

5. Построение ЛДФ при совпадающих средних признаков в классах для 2-D случая Рассмотрим наиболее простую ситуацию, когда пространство признаков двумерно. Тогда можно получить окончательное аналитическое решение для классификатора. Итак, пусть матрицы B ₁ и B ₀ имеют вид:

в 0 =

a

c

c b

B 1 =

df fe

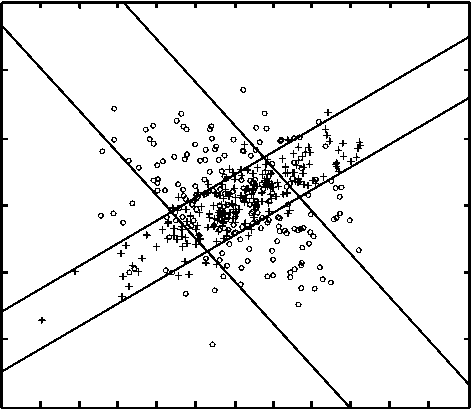
Рис. 7. Иллюстрация для a = b ≠ d = e

Работа выполнена при поддержке Министерства образования РФ, Администрации Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE).