О модификациях ромбических тайлингов, возникающих в обратной задаче о распределении ресурсов

Традиционные методы исследования технологической структуры производства, базируются на модели межотраслевого баланса. Однако в связи с тем, что замещение отечественных производственных факторов текущего пользования импортными сильно зависит от текущей экономической ситуации, нарушается гипотеза, о постоянстве затрат на. производство. В то время как Центральный Банк РФ поддерживает стабильный курс рубля, импортные производственные факторы вытесняют отечественные за. счет более высокой инфляции в России по сравнению с общемировой. Когда, возрастающие экономические трудности приводят к девальвации рубля, отечественные товары, наоборот, вытесняют импортные. Таким образом, для описания экономических агентов необходимо, в частности, описать процесс выбора, между отечественными и импортными производственными факторами текущего пользования.

Будем описывать технологическую структуру производства, с помощью обобщенной модели Хаутеккера-Иохансена (см. [1]). Рассмотрим отрасль, выпускающую однородную продукцию и использующую однородные производственные факторы текущего пользования, подразделяемые на. отечественные и импортные. Для некоторых отраслей (особенно обрабатывающих) мы не можем предполагать, что отечественные и импортные факторы являются полностью взаимозаменяемыми. Будем считать, что в отрасли имеются различные технологические процессы производства, каждый из которых требует разных затрат отечественных и импортных факторов для выпуска единицы продукции.

Пусть в отрасли имеются различные технологии, каждая из которых описывается вектором (жі,Ж2) характерной величины затрат отечественных (ад) и импортных (т₂) производственных факторов для выпуска, единицы продукции. Функционирование имеющихся в отрасли технологий будем описывать производственными функциями вида Ғ (—, —), где (н^) - вектор затрат отечественных и имиортных факторов. "1 "2

Определение 1. Эластичностью замеи^ения функции /(жі, Ж2) называется величина

^ |n( " ² ) при /(жі,Ж2) = const. Функция с постоянной эластичностъю замещения е >  0

/ Е- 1       Е- 1 \ Е — 1

(CES-функция) имеет вид J(жі, Ж2) = I ж1^Е + ж₂^Е I .

Данное понятие позволяет учесть неполную заменяемость производственных факторов:

при е ^ то она будет соответствовать линейной функции (полной заменяемости), при е = 1 она будет производственной функции Кобба-Дугласа, а при е ^ 0 соответствовать «уголку» — полной незаменяемости. Будем считать Ғ (•) функцией с постоянной эластичностью замещения е (CES-функцией).

Процессы перераспределения мощностей по технологиям и загрузки каждой технологии регулируются быстрыми процессами «оперативного управления», процессы изменения технологий являются медленными процессами «перспективного управления» отраслью.

Возьмем временной интервал в модели Хаутеккета-Иохансена достаточно большим, чтобы учитывать перераспределение производственных факторов по технологиям, одновременно будем считать технологии фиксированными на всем протяжении модели. Будем считать период между рассматриваемыми моделями времени достаточно большим (квартал), чтобы учесть процессы перераспределения мощностей по технологиям и загрузки каждой технологии. Изменение технологий, фактически изменение основных фондов, является медленным процессом и в рамках рассмотрения модели (5-10 лет) технологии можно считать постоянными.

Пусть ро >  0 — цена на выпускаемую отраслью продукцию и р = (р₁,р₂) — вектор цен на импортный и отечественный производственные факторы. Рассмотрим функцию Др), которая является преобразованием Юнга функции F (и), то есть

q(p) =

.        рп int.  —— u>0,F(и)>0 F(и)

,р G RL.

В частности, если F (и) - CES-функция с коэффициентом эластичности замещения е, то q(p') будет являться CES-фупкщіеіі (? коэффициентом эластичности | вида.

_— i

q(p') = (Д1 Х 1 )-^ + (р 2 Х 2 )-^) ^р ,                                (2)

где р = е — 1, р G [— 1; 0) U (0; то).

В [2] показано, что себестоимость производства единицы продукции по технологии соответствует вектору (х₁,х₂) и равна д(р₁х₁,р₂х₂). Технология х = (х₁,х₂) используется с максимальной интенсивностью, если она приносит прибыль, то есть д(р1Х1,р₂х₂) < ро-Если же убыточна, то есть Др1Х1,р₂х₂) > ро, то она не используется вовсе.

В настоящее время в России является доступной статистика индексов цен на выпускаемую отраслями продукцию (р0), однородные отечественные, импортные факторы (р1, р2), количество выпускаемой продукции (у*). Здесь и далее верхний индекс t отвечает за периоды времени из промежутка 1, 2,... ,Т , где Т - суммарное количество периодов времени. Распределение отраслей по технологиям и статистика потребления каждой технологией производственных факторов на микроуровне является недоступной. Для исследования соответствия коэффициента эластичности замещения отечественного и импортного факторов в обобщенной модели Хаутеккера-Иохансена статическим данным решается задача о существовании распределения отраслей по технологиям, соответствующим имеющимся статистическим данным: при заданных {(p0,P1,P₂,У*)|t = 1,... ,Т} определить, существует ли неотрицательная мера с носителем в R^, такая, что

У Ө(р 0 — q(p^t1 Х1,р2х2))р((1х) = у*,      t = 1,...,Т.                    (3)

0,х < 0, 1,х > 0.

Здесь Ө(^) - функция Хевисайда. Ө(х) =

Кривые, задаваемые уравнениями { q(p^t1Х1 ,р*>Х2), t = 1,...,Т}, разрезают положительный ортант R+ на области ai, г = 1, 2,... ,к. Пусть [Т ] — множество подмножеств множества точек 1, 2,..., Т.

Определение 2. Пусть каждая кривая q(p^t₁х₁,p^t₂ х₂) = р0 разобьет положительный ортант R+ на две части. Назовем положительной часть, содержащую точку (0, 0). Спектром области разрезания назовем множество номеров кривых, для которых данная область лежит в положительной части. Спектральной вершиной области с номером г — a_r назовем точку на булевском кубе {0|1}^т, соответствующую её спектру (для номеров, принадлежащих спектру, координаты спектральной положим единицам, для остальных номеров будем считать координаты нулями). Символом B обозначим множество спектральных вершин всех областей.

В [2] было показано, что разрешимость задачи соответствия коэффициента эластичности замещения статистическим данным равносильна вопросу принадлежности вектора динамики выпусков у = у1,..., ут конической оболочке множества всех спектральных верк шин областей cone(B) = ]д Агаг\«г Е В, Аг Е R+, к = 1, 2,...

г=1

В [3] мы рассматривали комбинаторные свойства класса таких конических оболочек. В работе исследуется задача определения подмножества допустимых значений коэффициента эластичности, т.е. значений, согласованных с вышеприведенной моделью при заданной статистике динамики цен и выпусков. Заметим, что если при малом изменении коэффициента эластичности замещения е в пределах одного знак а структура разрезания R² CES-кривыми не изменится, то оба значения е являются допустимыми или недопустимыми одновременно.

В данной статье мы рассмотрим комбинаторные свойства разрезаний положительного ортанта CES-кривыми и изменение этих разрезаний при изменении коэффициента эластичности замещения е.

2.    Модификации разрезаний положительного ортанта CES-кривыми

Теорема 1. Любые три прямые семейства

{(р1) ^РХ1 + (р2) ^рХ2 = 1\t = 1,...,т}                          (4)

имеют пересечение в R² не более, чем при одном р из днапазона [—1;0) U (0;+то).

Доказательство. Пусть для определенности р“ > р? > р₄- Чтобы точка пересечения

прямЫХ (р“ ) ^р + (Р2 )

р = 1.- (р?) ^-р+ (рО

р

= 1 лежала внутри положительного ортанта

R^, требуете я, чтобы р? >  р^. Аналогично, р2 >  Р?. Таким образом, будем считать, что Р2 > Р? > Р₂- Значение р, при котором три прямые пересекаются в одной точке, удовле-

творяет уравнению

(Р?)-р

(Р^

р

( р2 )^-р

(р2) ^{- р} 1

( р? Г 1

(р2 )^-р 1

= 0.

Это эквивалентно уравнению

((ARRCr кг-■) (Г-)

р

= 0.        (6)

Введем следующие обозначения:

(й=е-Чй =е-Л2;й)=еЛ3;й)=4          171

В силу неравенств р“ > р? > р₄ и р2 > Р? > Р2 ^{мы можем} считать, что А1, А2, A3, А4 > 0. Тогда уравнение перепишется в виде (е^Л1^р — 1) (е^Л2^р — 1) — (е^{- Л}3^р — 1) (е^{- Л}4^р — 1) = 0. Обозначим / (р) = (е^Л1р — 1) (е^Л2^р — 1) — (е^{- Л}3^р — 1) (е^{- Л}4^р — 1).

Лемма. Уравнение / (р) = 0; А₁, А₂, A3, А₄ > 0 имеет ровно одно решение в диапазоне (—то; 0) U (0; +то), если А₁А₂ = А3А4 и не имеет решений в диапазоне (—то; 0) U (0; +то), если А₁А₂ = АзА₄.

Доказательство. Заметим, что р = 0 является корнем этого уравнения второго порядка. если А1А2 = А3А4. II корнем как минимум третьего порядка, если А1А2 = А3А4.

Раскрыв скобки и умножив на е(Л3+Л4)р, перепишем уравнение в виде

/1 ^(р) = ^е

(Л1+Л2 + Лз+Л4)р

е(Л1+Лз+Л4)р

е(Л2+Лз+Л4)р + еЛ4р + еЛзр

— 1=0.

Пусть уравнение f (р) = 0 имеет не менее четырёх корней. Согласно теореме Штурма, уравнение f1 (Р) = (А1 + А2 + Аа + А4) е(Л1+Л2+л3+х4)р - (А1 + Аа + А4) е(А1+Лз+л4)р-- (Л2 + Аа + Л4) е(Л2+Лз+л4)р + Л4ел4Р + Аае^ - 1 = 0

имеет не менее трёх корней.

Умножив это уравнение на е (А1+л2+л3+л4)р) получим f2 (р) = (А1 + а2 + Аа + А4) - (А1 + Аа + А4) е Х2Р - (А2 + Аа + А4) е Л1Р+

+А4е-(Л1+л2+Лз)р - Аае-(Л1+Л2+Л4)р = 0.

Применив теорему Штурма ещё раз, получим, что уравнение f2 (Р) = (А1 + Аа + Л4) Л2е Х2Р + (Л2 + Аа + Л4) А1е Х1Р-

-Л4 (А1 + Л2 + Аа) е-(Л1+л2+Лз)р - Аа (А1 + Л2 + Л4) е-(Л1+Л2+л4)р = 0

имеет не менее двух корней.

Умножив это уравнение на е(А1+А2)р, получим уравнение fa (Р) = (А1 + Аа + Л4) А2е^1Р + (Л2 + Аа + Л4) А1еЛ2Р--А4 (А1 + А2 + Аа) е А3Р - Аа (А1 + А2 + А4) е А4Р = 0.

Применим взятие производной последний раз, получим, что уравнение

Д (Р) = (А1 + Аа + Л4) А2А1е^1Р + (Л2 + Аа + Л4) А1А2е^2Р+ +А4Аа (А1 + А2 + Аа) е А3Р + А3А4 (А1 + А2 + А4) е А4Р = 0

имеет не менее одного корня.

Однако, т.к. А1, А2, A3, А4 > 0, в выражении Д (р) все коэффициенты перед экспонентами положительны, и УЗ (р) > 0, противоречие.

Таким образом, уравнение ( е^Х1Р - 1) (е^Л2^Р - 1) - (е^-Л3^Р - 1) (е^-Л4^Р - 1) = 0 имеет не более трёх корней на R. Если А1А2 = А3А4, корней, кроме р = 0, нет.

Если А1А2 = А3А4, то f‘‘ (р) = 0, и в окрестности точки р = 0 выражение f (р) сохраняет знак. Так как lim f (р) = +w, a lim f (р) = -то, обязан существовать ненулевой корень р^ +^            р^—^

уравнения f (р) = 0. Лемма и теорема доказаны.

^Р Х2 = 1|t = 1, . . . ,Т|

Следствие 1. Любые три прямые семейства {(р1) ^р х1 + (р2)

имеют пересечение в R+ ровно при одном р из диапазона [-1;0) U (0;+то), если верно, что из неравенства р“ > p^f > р1 следует не равенство Р2 > р₂ > р₂ и верно одно из следующих условий:

Г) f ‘‘ (0) < 0

или

2) f‘‘ (0) > 0,f (-1) < 0.

Иначе данные прямые не имеют пересечения при Ур € [-1;0) U (0;+то).

Доказательство. Теорема гласит, что больше одного корня на указанных промежутках существовать не может. Покажем существование хотя бы одного. Заметим, что из доказательства теоремы следует, что без выполнения последнего условия с неравенствами корней не будет, т.о., будем считать его выполненным. Если выполнено первое условие, то с учетом того, что / (0) = 0,/‘ (0) = 0 и lim / (р) = +то, у функции / (р) обязан суще-р^+^

ствовать корень на промежутке (0; +то). Ес ли /‘‘ (0) > 0, то при вышеуказанных условиях у функции / (0) = 0, /‘ (0) = 0 вер но: 35 € [—1;0) : / (5) > 0. В совокупности с условием / (—1) < 0 это гарантирует корень на промежутке [—1;0).

Если условия следствия 1 неверны, то возможны 2 случая.

Первый случай — /‘‘ (0) > 0 и / [—1) > 0. Так как lim / (р) = —то, существует корень р^—^

на промежутке (—то;1]. Из доказательства теоремы следует более общее утверждение о том, что функция / (р) имеет не более одного нуля на промежутке (—то; 0) U (0; то), следовательно, более корней на [—1; 0) U (0; +то) нет.

Второй случай - /‘‘ (0) = 0. С учетом условий / (0) = 0, /‘ (0) = 0. lim / (р) = —то. р^—^

lim / (р) = той возможности не более одного корня на (—то; 0) U (0; то) существует толь- р^^

ко одна возможность существования корня на (—то; 0) U (0; то) - касание в этом корне оси ож. Тогда у /‘ (р) гарантируется существование хотя бы двух нулей производной на (—то; 0) U (0; то) - в уже упомянуютой точке касания с осью ож, а также в какой-то точке на промежутке между вышеупомянутой и точкой 0 — там, где / (р) обязана достигать максимум или минимум по теореме Ролля. Из доказательства теоремы следует невозможность наличия трёх корней у производной /‘ (р) на (—то; то), также приходим к противоречию.

Следствие 2. Любые три CES-кривые семейства

{((ріжі) р + (р2ж2) р) Р = Р0к = 1,...,Т}(14)

имеют пересечение в R+ не более, чем при одном р из диапазона [—1;0) U (0;+то).

р 2 р О

Для доказательства этого следствия нужно отнормировать цены: р) = ^;р0 1р0 -2

р ——— р и затем сделать замену жі = жі ;ж2 = ж2 , затем воспользоваться исходной теоремой. Следствие 1 будет указывать на условия, при которых такой корень является на промежутке [—1; 0) U (0; +то) единственным.

Таким образом, при изменении коэффициента эластичности замещения р количество разных структур разрезания (т.е. множеств спектральных вершин B) является конечным и не превышает (С^ + 2) («+ 2», а не «+ 1» в с вязи с тем, что в точке р = 0 происходит также «разрыв» со сменой структуры разрезания).

Рассмотрим понятие ромбических тайлингов, позволяющих проанализировать изменение структуры разрезания при переходе р через значение, соответствующее пересечению трех CES-кривых.

3.    Ромбические тайлинги

Заметим, что порядок пересечения CES-кривых разрезания с осями координат зависит от упорядочивания величин ^ (для оси ожі) и ^2 (для оси 0Ж2), г де t = 1, 2,...,Т и не Р0                           _ Р0

зависит от величины р. Упорядочим номера CES-кривых в порядке их пересечения с ожі, начиная от начала координат.

Рассмотрим спектры областей, примыкающих к оси ожі. Это будут спектры {0,..., 0, 0}; {0,... 0,1}; {0,..., 1,1};...; {1, 1,..., 1}. Рассмотрим Т-мерный гиперкуб, на котором отметим спектральные вершины этих областей, соединим соседние вершины отрезками, а затем сделаем параллельную проекцию полученной цепи на подходящую плоскость так, чтобы на этой плоскости были нарисованы стороны половины правильного 2Т-угольника (где Т — количество прямых или проволок).

Отметим все оставшиеся спектральные разрезания, соединим соседние отмеченные вершины отрезками и спроецируем все остальное той же параллельной проекцией. Полученная фигура будет состоять из ромбов и являться ромбическом тайлингом, который изучается, например, в [4]. Эта фигура позволяет наглядно изобразить множество спектральных вершин на плоскости и изучать их свойства.

Дадим определение ромбического тайлинга, не связанное с вышеприведенной проекцией.

Рассмотрим правильный 2Т-угольник с единичными сторонами SqS1 .. . S2T -1- Введем следующие обозначения: C_t = (St-1 S_t), t = 1,...,Т. Будем считать вектор, равный (C_t), обладающим цветом t.

Определение 3. Ромбическим тайлингом называется «правильное» разбиение 2Т- угольника Sq Si ...82т-1 ^на ромбы с единичными сторонами, параллельными каким-либо сторонам исходного 2Т-угольника. Здесь под «правильным» разбиением имеется в виду разбиение без пустот и наложений ромбов друг на друга.

Важным в теории ромбических тайлингов является понятие змейки.

Определение 4. Змейкой ромбического тайлинга называется упорядоченная последо-

7^     7^

7^

вательность векторов С_о1 ,С_о2,...,С<т_Т, начатая из точки Sq, так что каждый новый отложенный от суммы предыдущих вектор является границей каких-либо ромбов разбиения

2 Т-уголышка. Здесь ст = ( ^ст 1

^ 2

^ 3

7^   7^

.

.

.

.

.

.

Т \

- элемент симметрической группы S_n. ст_п /

Дополнительно последовательность С1, С2,..., Ст называется нижней змейкой.

7^     7^

7^

Определение 5. Пусть последовательность векторов С_о1 ,Са2,...,С_ОТ задает змейку. Фигуру, заключенную между данной змейкой и нижней змейкой, разбитую «правильным»

7^     7^

7^

образом на ромбы, назовем частичним ромбическим тайлингом. Змейку С_о1 , Со-2,..., С частичного тайлинга назовем верхней.

Понятие частичных ромбических тайлингов является обобщением понятия «обычных» ромбических тайлингов, и именно эта фигура будет получена в результате проекции пространственного графа спектральных вершин разрезания. В связи с этим все ромбические тайлинги в дальнейшем будут считаться частичными. Отметим, что все частичные ромбические тайлинги, полученные при соответствии разрезаниями CES-кривыми при различных коэффициентах эластичности замещения, имеют одну и ту же верхнюю змейку.

Видоизменим определение змейки применимо к частичному ромбическому тайлингу.

Определение 4’. Змейкой частичного ромбического тайлинга называется не вы ходящая за пределы данного тайлинга упорядоченная последовательность векторов Со-1, Сст2,..., Сстт, начатая из точки Sq, так что каждый новый отложенный от суммы предыдущих вектор является границей каких-либо ромбов разбиения 2Т-угольника.

Определение 6. Вершиной ромбического тайлинга называется вершина любого из ромбов разрезания данного тайлинга. Спектром вершины R назовем подмножество Sp(R) чисел из множества. {1, 2,..., Т}. такіьт что S q R = ^ Ct-

teSp(R)

Определение спектра вершины имеет смысл, т.к. из точки Sq можно дойти до любой вершины R по векторам цветов t = 1,..., Т. Так, точка S3 имеет спектр {1, 2, 3}.

Предложение 1. Информация о спектрах всех вершин позволяет однозначно восстановить (частичный) ромбический тайлинг.

Для этого достаточно обозначить по формуле (SqR) = ^ Ct, восстановить положе- tGSp(R)

ние всех вершин и соединить отрезками «соседние» вершины, спектры которых отличаются ровно на. один индекс.

Приведенное предложение позволяет построить ромбический тайлинг, соответствующий разрезанию, не пользуясь понятием проекции.

Предложение 2. Ромб ромбического тайлинга, соответствующим разрезанию R² прямыми или строгой проволочной, будет указывать на. пересечение двух прямых между собой, причем цвет ребер ромба, будет соответствовать номерам пересекающихся прямых.

Зададим CES-кривые разрезания уравнениями в полярных координатах r_t (ш), t = 1, 2,...,Т, 0 6 ш 6 2- Если упорядочить точки пересечения кривых по увеличению их аргумента ш, мы можем упорядочить и пронумеровать ромбы ромбического тайлинга.

Пусть зафиксирована переменная 0     6 ш 6     2, а перестановка

1    2   3

< 1   <72 <73

т

On

)

Е    St определяет порядок расположения величин

т 1 (ш),... ,т_т (ш) : т_ст1 (ш) < /Д2(ш) < • • • <  т_СТт (ш). Здесь тфш),   t = 1, 2,... ,Т, 0 6 ш 6 2 -

задание исследуемых CES-кривых в полярных координатах. Тогда в ромбическом тайлинге —   —       —

присутствует змейка, соответствующая порядку векторов —_СТ1 , —_Ст2,..., —_стт.

При увеличении ш от 0 до т2 этот порядок меняется толь ко при проходе переменной ш через значение, в котором две проволоки имеют пересечение. Данное пересечение в ромби ческом тайлинге будет соответствовать ромбу с номером. Пронумеровав ромбы в порядке увеличения величины ш, мы получим нумерованный ромбический тайлинг.

Определение 7. Нумерованным ромбическим тайлингом называется ромбический тайлинг с заданной нумерацией ромбов 1, 2,..., R, обладающей следующим условием: V т 6 R объединение нижней змейкіі іі всех ромбов с поморами 1, 2,..., г является ромбическим тайлингом.

Таким образом, не всякая нумерация ромбов ромбического тайлинга порождает нумерованный ромбический тайлинг. Нумерация ромбов ромбического тайлинга позволяет ввести соответствующую нумерацию змеек нумерованного ромбического тайлинга.

Определение 8. Будем считать, что объединение нижней змейки и всех ромбов с номерами 1, 2,... ,г является фигурой, ограниченной двумя змейками: нижней и змейкой с номером г.

Упорядочивание точек пересечения CES-кривых по увеличению аргумента позволяет построить нумерованный ромбический тайлинг, соответствующий разрезанию алгоритмически, зная уравнения CES-кривых. Однако в нумерованном тайлинге содержится излишняя информация: для исследования соответствия коэффициента эластичности замещения отечественного и импортного факторов статистиским данным достаточно знать спектры областей, что соответствует простому (ненумерованному) ромбическому тайлингу.

Частой процедурой изменения тайлинга является флип. Пусть 1 6 г < j <  к 6 Т, а H_—ij_k =    ^     a_t—, a_t Е {0,1} — сумма некоторых векторов тайлинга, не содержа-

16t6T,t=i,j,k щая вектора цвета г, j, к.

Определение 9. Флипом называется следующая операция, при которой два тайлинга переходят друг в друга: замена вершины — j + 5-.^ на вер шину —_i + —k + ’H_-ijk или обратная замена, где H—ijk — одна и та же сумма некоторого количества оставшихся векторов, составляющих тайлинг, при обязательном присутствии в обоих ромбических тайлингах шести «соседей» - вершин H—ijk'. —і +5-^: —к +H-ijk- —і +— j+H-_ijk. —j +—k 'H _;/ —j +—j +—k +H-ijk- Геометрически флипом является следующая замена, указанная на рисунке.

Предложение 3. (см. [4]). Любые два тайлинга с совпадающими нижней и верхней змейкой можно получить друг из друга с помощью применения операции флипа конечное число раз.

Предложение 4. Модификация ромбического тайлинга, соответствующая проходу коэффициента р через значение, соответствующее переечению трем CES-кривым в одной точке, является флипом.

При попарно трансверсальном пересечении трех CES-кривых г, j, к (см. рис. 1) в одной точке к точке пересечения примыкают б областей. Эти области сохраняются и в момент, предшествующий пересечению, и в момент, следующий непосредственно за пересечением, — эти области и являются шестью «соседями», необходимыми для проведения операции флипа. В момент, предшествующий пересечению трех CES-кривых в одной точке, присутствует область, соответствующая области —i + Е-^, при переходе р через значение, соответствующее переечению, эта область исчезает и вместо неё появляется область —j- + —k + H-ijk или наоборот. Это и соответствует флипу.

Теорема 1 и её следствия в терминах ромбических тайлингов утверждает, что

• 1)    при изменении р в пределах каждого промежутка [—1;0) и (0;+то) получается цепочка ромбических тайлингов,

  

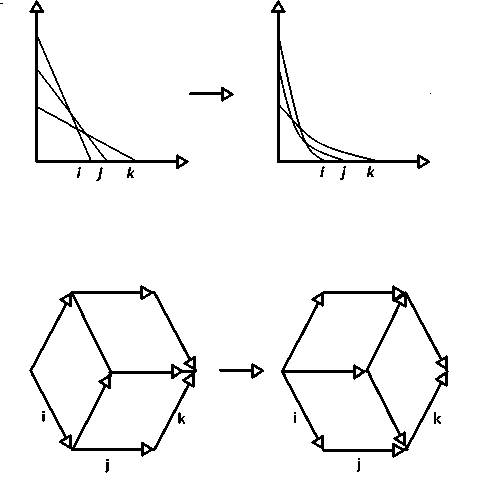
  Рис. 1. Флип ромбического тайлинга, возникающий при изменении коэффициента эластичности замещения

  
  

• 2)    каждая пара соседей-тайлингов по цепочке отличается друг от друга операцией флипа,

• 3)    флип, соответствующий каждой тройке номеров i,j,k, может происходить не более раза в сумме в обоих промежутках.

Определение 10. Назовем тройку CES-кривых i, j, к флипующимися, если порядок их пересечения с осью oxi полностью обратен порядку пересечения с осью 0x2. Это условие является в теореме 1 необходимым для того, чтобы при изменении коэффициента эластичности замещения е возможно было существование пересечения трех кривых в одной точке при некотором р Е [—1; 0) U (0; +то), где р = е — 1.

Обозначим величиной |a| количество беспорядков (таких пар (i,j ); 1 6 г < j 6 Т,

что at > aj^ в перестановке a =

(

Т

On

пересечения кривыми семейства

{ ((Р1Х1) ^Р + (р2Х2) ^р^

1 р

^ которая определяет порядок

перестановки относительно этого порядка на оси oxi.

= p^t = 1,...,т}

оси 0x2, как

Предложение 5. Максимальное количество флипов в обоих промежутках р Е [—1;0)

и р Е (0; +го) суммарно ограничено количеством флипующихся троек CES-кривых и не

№—2) 3

может превышать

Доказательство. Заметим, если тройка i,j,k являетя флипующейся, по следствию из теоремы 1 в случае, если AiA2 = A3A4, обязано существовать ровно одно решение при р Е (—^; 0) U (0;+^), ио может и не существовать при р Е [—1; 0) U (0;+^), из этого следует ограничение сверху на количество флипующихся пар. С другой стороны, каждый беспорядок перестановки a участвует не более чем в Т — 2 флипующихся тройках, причем каждая такая тройка содержит 3 беспорядка, отсюда оценка І^Д—2). Эта оценка достигает

максимума в С^ если a =

(Т

Т —

Т —

Т

Работа поддержана РФФИ №12-07-31231_мол_а, №12-07-33007-мол_а_вед, №11-07-00162_а, №13-07-13110_офи_м_РЖД; Министерством образования и науки Российской федерации №14.А18.21.0866