О наблюдаемости кристаллических решёток по изображениям их проекции

Решение многих фундаментальных и прикладных научных задач требует проведения предельно точных измерений параметров элементарной ячейки различных веществ. Параметры элементарной ячейки являются важными характеристиками кристалла и зависят от химического состава, типа химической связи, температуры, дефектности кристаллической решётки и напряжений, возникающих при деформации кристалла. [1]. В настоящей статье рассматриваются геометрические параметры элементарной ячейки, определяющие структуру кристаллической решётки.

Расположение атомов вещества в кристалле характеризуется периодическим повторением элементарной ячейки. Геометрически элементарную ячейку можно охарактеризовать тремя векторами a , b , c или шестью скалярными величинами a , b , c , α , β , γ (рис. 1).

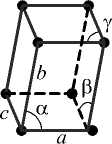
Рис. 1. Параметры элементарной ячейки

В зависимости от соотношения линейных и угловых параметров кристаллы можно разделить на семь систем – сингоний. Если одновременно указать сингонию и возможный способ центровки ячейки, то можно получить все 14 типов кристаллических решёток – решётки Бравэ [2].

Метод рентгенографии, предназначенный для идентификации кристаллических веществ, основан на том, что индивидуальность кристаллической структуры соединения обуславливает индивидуальный вид его рентгенограммы. Кристаллы являются дифракционной решёткой для рентгеновских лучей и пучков электронов ввиду того, что длины их волн соизмеримы c межатомными расстояниями кристалла. Угол дифракции и длина волны излучения связаны постоянным соотношением, определяемым уравнением Вульфа–Брэгга [3]. Определённое число дифракционных максимумов и их фиксированное положение на рентгенограмме соответствует набору межплоскостных расстояний. Практически нет различных кристаллических веществ, рентгенограммы которых совпадали бы полностью.

Рентгенографический анализ позволяет определить сингонию кристаллической решётки и геометрические параметры элементарной ячейки. Установление соответствия между индексами узлов решётки и дифракционными пиками известных структурных типов проводят путём сопоставления экспериментально полученной рентгенограммы с имеющимися в базах данных или полученными при расчёте теоретической ди-фрактограммы. Однако успех решения зависит от того, к какой сингонии принадлежит кристалл и насколько много априори известно о его строении, поэтому задача определения геометрических параметров является сложной и не всегда однозначно решаемой [4].

Монокристальные рентгеновские методы, а также просвечивающая электронная микроскопия (ПЭМ) позволяют получать неискажённые изображения узловых сеток, так называемых обратных решёток (рис. 2) [5].

Обратной называется пространственная решётка, которая образована векторами, величины которых равны обратным межплоскостным расстояниям, а направления перпендикулярны семейству плоскостей исходной решётки. Обратная решётка является Фурье-образом прямой кристаллической решётки [2].

Рентгеновские методы позволяют получать фотографии сечений обратной решётки для её различных слоёв (рис. 2а). Особенностью изображений электронной дифракции является то, что все сечения обратной решётки, полученные при помощи ПЭМ, проходят через начало координат ячейки, при этом фактически наблюдается Фурье-образ решётки (рис. 2б) [6].

а)                               б)

Рис. 2. Электронные изображения обратных решёток: рентгеновская дифракция (а), дифракция электронов (б)

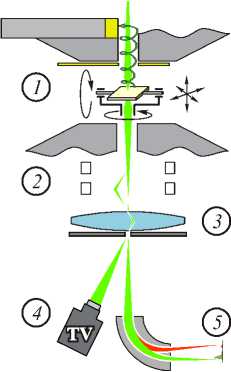
При проведении исследований в электронном микроскопе образец (объект) обычно помещают в специальный держатель на тонкой металлической сетке. Держатель можно электрическим способом плавно перемещать по трём координатным осям. Для изменения наклона образца во время наблюдения используется гониометрическое устройство, которое имеет две взаимно перпендикулярные оси наклона, лежащие в плоскости образца и приспособленные для его вращения на 360°. При наклоне устройство обеспечивает неизменность положения объекта относительно оси микроскопа (рис. 3). В этой статье будем рассматривать только вращательное движение объекта исследования.

гается использовать теорию описания кинематики вращательного движения системы материальных точек с использованием дифференциальных кинематических уравнений и элементы общей теории наблюдения и управления динамическими объектами.

1. Преобразование координат

Воспользуемся известными положениями из теории кристаллографии [2]. Для определения декартовых координат узла решётки, индексированного в системе её координат решётки, можно выписать

следующие соотношения:

' * 1

* ²

V * 3 )

'

a

V

b cos у b sin у

) c cos в

- c cos a * sin в

v

/ c )

' n ₁

n

1 ¹ L ’ 2 L . L

,

V n 3 )

где a , b , c , a , в , Y — параметры, определяющие эле

ментарную ячейку решётки (рис. 1), ( n 1 L , n 2 L , n ₃ L ) ,

n ^L е X - индексы узла, ( * 1 , * ₂, * ₃ ) , х_к е К - декар -

товы координаты узла в системе координат решётки X , задаваемой базисными векторами X ₁ , X ₂ , X ₃ , точка O является началом координат, в которой находится узел с индексами ( 0,0,0 ) .

Соответствующие параметры ячейки обратной решётки a * , b * , c * , a * , в * , Y * определяются как:

a * = bc sin a / V , b * = ac sin в / V , c * = ab sin Y / V ;

cos a * = ( cos в cos y- cos a ) / sin в sin y ;

cos в * = ( cos a cos y- cos в ) /sin a sin y ;

cos y * = ( cos a cos в — cos y ) / sin a sin в ;

где V – объём ячейки:

V = abc x x1 + 2cos a cos в cos y-cos2 a- cos2 в — cos2 y .

Пример 1: для кубической ячейки

(a = b = c, a = в = Y = n /2):

Рис. 3. Схема просвечивающего электронного микроскопа: 1 – держатель объекта, 2 – отклоняющие системы, 3 – система увеличения, 4 – система регистрации, 5 – щель спектрометра

Постановка задачи анализа изображений кристаллических решёток рассматривалась в работах [7] и [8]. Было показано, что при рассмотрении задачи восстановления решётки по проекциям или, в частном случае, определения её параметров, необходимо ввести некоторую характеристику, которая показывала бы, насколько полно рассматриваемый объект представлен на той или иной проекций. Это приводит к постановке новой для математики задачи о наблюдаемости сложной трёхмерной решётки по её проекциям.

Для определения наблюдаемости проекций кристаллических решёток в настоящей работе предла-

' * 1 >		' a 0 0"	' П 1 L '
* 2	=	0 a 0	n 2 L	.                               (2)
Y V * 3 )		v 0 0 a ?	V n 3 L )
Пример 2: для моноклинной ячейки ( a = Y = п /2 ) :

' * 1 >		' a	0	c cos в	' П 1 L Л
* 2	=	0	b	0	n 2 L	.                         (3)
Y V * 3 )		V 0	0	c sin в 7	V n 3 L )

Введём базовую систему координат Y , определяемую базовыми векторами Y ₁ , Y ₂ , Y ₃ , точка O является началом координат и совпадает с началом координат в системе координат, связанной с решёткой.

В начальный момент системы координат X и Y совпадают. Далее система координат решётки X осуществляет произвольный поворот в системе координат Y относительно начала координат.

Рассмотрим задачу определения декартовых координат узлов решётки, осуществляющей вращение, в базовой системе координат. В соответствии с теоремой Эйлера – Даламбера всякое перемещение системы материальных точек, имеющей одну неподвижную точку, может быть заменено одним конечным поворотом вокруг оси, проходящей через неподвижную точку.

Пусть решётка осуществляет вращение относительно оси конечного поворота, задаваемой вектором 6 , проходящей через точку O , на произвольный угол — , у _к - угол между осью конечного поворота и осью Y k , c k = cos у k - направляющие косинусы вектора 6 в системе координат Y (рис. 4).

Для описания преобразования координат воспользуемся параметрами Эйлера или Родрига-Гамильтона % j , j = 0,1,2,3, которые являются одними из основных кинематических параметров углового движения твёрдого тела [9].

% = cos ^— , %. = c. sin ^— , к = 1,2,3.

0     2 kk 2

Нормировка параметров определяется соотношением:

% ₀ ² + % 1 ² + % ₂ ² + % ₃ ² = 1.

Для удобного математического обозначения положения и вращения объектов в пространстве будем использовать описание с использованием кватернионными матрицами [10]. Тогда связь координат узла решётки в декартовой системе координат с координатами в базовой системе координат устанавливается соотношением:

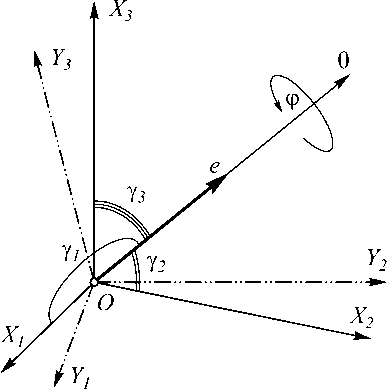
Рис. 4. Схема вращения системы координат решётки X относительно базовой системы координат Y

( 0, y 1 , y ₂, y ₃ ) = n ( % ) ( m ( % ) ) T ( 0, x 1 , x ₂, x ₃ ) ,          (6)

где m ( % ) и n ( % ) - кватернионные матрицы поворота, определяемые на основе параметров Эйлера [9, 10]:

	Г % 0	-% 1	-% 2	-% 3 "
m ( % ) =	% 1 % 2	% 0	-% 3	% 2
		% 3	% 0	-% 1
	v % 3	-% 2	% 1	% 0 7
	Г % 0	-% 1	-% 2	-% 3 )
	%,		% 3 % 0	-% 2 % 1
n ( % ) =	1 % 2	0 -% 3
	v % 3	% 2	-% 1	% 0 7

Используя (7) и (8), выражение (6) можно записать в виде:

Г y )

y ²

v y 3 7

' % 0 ² +% 1 ² -% 2 ² -% 3 ² 2( % 1 % 2 -% o % 3 )

_V 2( % 1 % ₃ + % ₀ % ₂)

2( % 1 % 2 + % ₀ % ₃) % ₀ ² -% 1 ² +% ₂ ² -% ₃² 2( % ₂ % ₃ -% ₀ % 1 )

2( % 1 % 3 -% 0 % 2 ) ' 2( % 2 % 3 +% 0 % 1 )

% ₀ 2 -% 12 -% ₂ 2 +% ₃ 2 ,

Г X 1

x ²

v ^x 3 7

• 2.    Уравнение состояния. Уравнения наблюдения. Условие наблюдаемости

В этом разделе будем опираться на теорию кинематического движения системы материальных точек [11, 9]. Рассмотрим систему материальных точек, являющихся узлами кристаллической решётки, осуществляющую вращательное движение. Уравне- ние наблюдения узла системы можно записать, используя полученные выражения для преобразования координат. Введём функции наблюдения координат узла решётки в базовой системе координат:

Z k ( % 0 , %_p % 2 , % 3 ) = У к .

Получим систему уравнений наблюдения

[ z. (%,,, % , %₂, %) = (%,² + % ² -%₂ ² -%₃ ²) x + 2(%.%₂ + %„%₃) x ₂ + 2(%.%₃ - %„%₂) x , 1      0 , 1 , 2 , 3            0          1          2          3      1            1 2        0 3 2            1 3        0 2 3 ,

< z ₂ ( % ₀, % 1 , % ₂, % ₃ ) = 2( % 1 % ₂ - % ₀ % ₃) x 1 + ( % ₀ ² -% 1 ² +% ₂ ² -% ₃²) x ₂ + 2( % 2 % ₃ +% ₀ % 1 ) x ₃,                                (10)

z ₃ ( % ₀, % 1 , % ₂, % ₃ ) = 2( % 1 % ₃ +% ₀ % ₂) x 1 + 2( % 2 % ₃ -% ₀ % 1 ) x ₂ + ( % ₀ ² -% 1 ² -% ₂ ² +% ₃²) x ₃.

Уравнение состояния для системы можно записать, используя дифференциальные кинематические уравнения в параметрах Эйлера [11]. Введём функции tok (t), являющиеся проекциями угловой ско- рости вращения на оси системы координат Y . В случае, когда составные угловой скорости вращения являются константами, дифференциальное уравнение вращения можно записать в матричном виде:

	f % 0 Л ɺ		0 to.	—0 1 0	—0 2 0 3 0	—° , 1 —° 2 to ,	f %0' % ,
2	1 % 2	=	1 0 2	—0 3			% 2	.          (11)
	l % 3 )		1 ° 3	0 2	—0 1	0 v	l % 3 V

ределить значения вектора состояния % j ( t ) в любой момент t , принадлежащий этому отрезку.

Критерием наблюдаемости является условие – якобиан:

Здесь параметры Эйлера % j ( t ) представлены как функции, зависящие от времени t . % j есть производные параметров % j ( t ) по времени t .

Таким образом, функции zk также являются зависящими от времени t, и существуют производные zɺk , ɺzɺk ,ɺzɺɺk ,…, выражение для которых можно запи-дkz дz дk% сать в матричной форме в виде: —= =--г, где дtk д% дtk производные дk%/дtk можно вычислить, используя выражение (11).

Согласно [12], если имеются непрерывные наблюдения за изменением функции z ( t ) на интервале [ t ₀, t ₁] , для вполне наблюдаемой системы можно оп-

I =

дФ д%

* 0,

где Ф T = ( z^T , Z T , Z T ,... ) .

Введём обозначения: a 0 = % 0 x i +% 3 x 2 - % 2 x 3 , a , = % , x , + % ₂ x ₂ + % ₃ x 3 , a 2 = % 2 x i - % 1 x 2 + % 0 x 3 , a з = % з x , — % 0 x 2 — % , x 3 .

Вычислим матрицы производных:

( an a — a — a)

д z , °      ^{1       2       3}

д% = 2 - a3 a 2 a, - a 0 , l a2    a3 a0     ai )

—a 2 0 2 — a 3 ^ 3 — a 3 0 2 + a 2 0 3 — a 0 ^ 2 + a , 0 3 — a , 0 2 — a 0 ^ 3

— = 2 a , ® , — a ₀ m ₃     a 3 ц — a ₁ to ₃     a 0 0 , + a ₂ to ₃     a ₁ to ₁ + a ₃ to ₃

д% i a3^1 + a0^2 — a2^1 + a, 0 — a,0i — a2Ц a0^ — a3^2 ,

Наблюдение решётки будем осуществлять проецированием координат узлов решётки в базовой системе координат Y на плоскость Y2OY3. Поскольку имеются наблюдения только двух координат, то матрицу Ф можно записать в виде:

^Ф T = ( ^Z 2 ^Z 3 ^Z2

Z ₃ ) . Таким образом, матрица якобиана I примет вид:

(

— a 3

a ₂

a ₁

— a ₀

I = 2

a ₂

a₁ to ₁ — a ₀ to ₃

i a 3 ^ц + a 0 ^ 2

a ₃

a ₃ to, — a ₁ M ₃

— a 2 ® i + a , 0 2

a ₀

a ₀ to , + a ₂ to ₃

— a ^u, — a 2 ц

ai a1o1 + a 3to3 a 0°i — a 3°2 v

Условие наблюдаемости (12) можно записать в виде:

det I = to , to ₂ a ₁ ( a ₁ — a ₂ ) ( a ₀ ² + a ₁ ² + a ₂ ² + a ₃ ² ) ^ 0. (17)

Проецируя на плоскость наблюдения Y 1 OY 2 , можно получить аналогичное выражение. Проецируя на плоскость наблюдения Y 1 OY 3 , можно получить, что определитель I равен 0, однако добавление в матрицу Ф третьей пары наблюдения в виде вторых производных даёт выражение, аналогичное (17).

Следует отметить, что, поскольку максимальное число доступных наблюдений для одного узла решётки равно 4 (координаты точки на плоскости и производные координат точки), использование только двух узлов на проекции даёт возможность определить только 5 параметров наблюдения (включая углы поворота и параметры самой решётки). Если наблюдение кристаллической решётки характеризуется числом параметров больше 5, определить параметры решётки по одной проекции невозможно и требуется использование большего числа проекций. При этом развиваемый подход к исследованию наблюдаемости полностью сохраняется.

Вернёмся к наблюдению одной проекции. Поскольку число параметров наблюдения % j равно 4, при ранге матрицы I , равным 4, выполняется необходимое условие наблюдаемости и система, определяющая вращение кристаллической решётки в пространстве вокруг центрального узла, является наблюдаемой , в противном случае при ранге матрицы I , меньше 4, система не будет являться наблюдаемой (будет ненаблюдаемой ).

Из (17) можно определить условия, при которых система будет ненаблюдаемой. Запишем уравнение det I = 0, получим:

0 ^ 0 2 a i ( a i — a 2 ) ( a 02 + a / + a 22 + a 3 ² ) = 0 .       (18)

Отметим, что, учитывая (13) и (5),

(2 .     2 .      2 .      2 A a 0 + ai + a 2 + a 3 ) =

= ( x , ² + x ₂ ² + x ₃ ² )( % ₀ ² +% ₁ ² +% ₂ ² +% ₃ ² ) =

= ( x , ² + x ₂ ² + x ₃ ² ) .

В итоге получаем условие, при выполнении которого система будет ненаблюдаемой:

® 1 ® ₂ a 1 ( a 1 - a 2 ) ( x² + x 22 + x 32 ) = 0 . (19)

Из анализа условия (18) можно сделать следующие выводы:

• 1)    В выбранном начальном положении (узел решётки ( 1,0,0 ) находится на оси X 1 ) при наблюдении узла (0,0,0) система решётки не будет являться наблюдаемой.

• 2)    Если проекции угловой скорости вращения ц = 0 или to ₂ = 0 , система также не является наблюдаемой. Это соответствует вращениям вокруг координатных осей, как показано на рис. 5, для кубической ячейки.

• 3.    Анализ достаточных условий наблюдаемости кубической ячейки

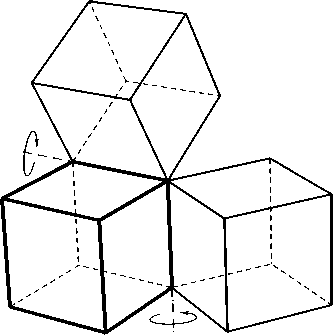
Рис. 5. Схема вращения решётки относительно координатных осей

Нетривиальным условием в выражении (18) является выражение а1 (а1 - а2 ) = 0.                                       (20)

Заметим, что уравнение (20) необходимо разрешать относительно параметров наблюдения % k , связь с переменными a _k задаётся выражениями (13). Рассмотрим решение этого уравнения для некоторых частных случаев.

Запишем условие (20), учитывая обозначения (13), (4) и выражение (2) при наблюдении различных узлов кубической ячейки, в виде таблицы соответствий 1.

Наблюдаемость узлов невозможна в случаях:

ф

• 1)    sin — = 0, т.е. ф = 2 п k , k е Z - соответствует полному обороту решётки.

• 2)    c 1 c ₂ c 3 = 0 - соответствует вращению вокруг осей координат.

• 3)    ( c 1 + c ₂)( c ₂ + c ₃)( c 1 + c ₃)( c 1 + c ₂ + c 3 ) = 0,

ф 1           ф 1

tan— =---------, tan— =------ - соответствуют

2 c 1 ± c ₂ + c ₃       2 2 c 1 + c ₃

случаю, когда узлы на проекции выстраиваются по вершинам квадрата, равного грани куба (рис. 6).

Таблица 1. Выражения, определяющие ненаблюдаемость узлов кубической ячейки

Узел	Выражение
( 1,0,0 )	• 2 Ф /          х /ч c 1sin “( c 1 - c 2) = 0
( 0,1,0 )	• 2 ф /     . х /ч c 2 Sin —( c + c 2) = 0
( 0,0,1 )	■ ф Г ■ ф      ф Г А c Sin— c Sin--cos— = 0 3 2 ( 3 2       2 J
( 1,1,0 )	/    . . ■ ф Га ■ ф Га ( c . + c , ) sin — 2 c . sin — = 0 v 1 2) 2( 1 2 J
( 0,1,1 )	( . X • фГ/ .     . x • ф       ф Га c + c sin— ( c , + c. + c. )sin cos— = 0 v 2 3)     2 (v 1 2 32     2        2 J
( 1,0,1 )	X ■ ф C             ■ ф      ф Га ( c , + c-. ) sin— ( c, - c3 + c-. )sin--cos— = 0 \ 1     3;     2 (v 1     2     32     2         2 )
( 1,1,1 )	f c , + c, + c ,)sinф (2 c , + c ,)sinф - cosф = 0 i 12 372 (v 1 32    2      2 J

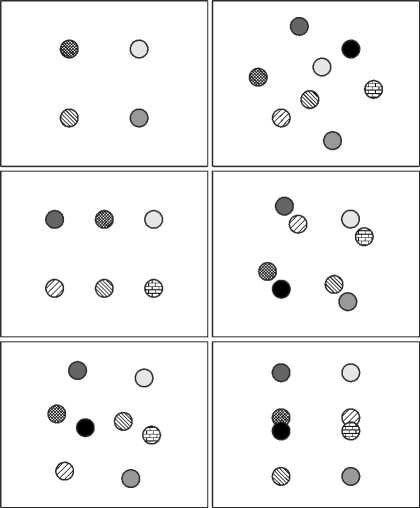
Рис. 6. Схемы проекций узлов кубической ячейки, при которых решётка является ненаблюдаемой

В случаях, когда узлы решётки являются наблюдаемыми, используя (9), можно записать систему алгебраических уравнений второй степени для оценивания параметров наблюдения % _k и длины стороны a . Выражение (5) даёт дополнительное уравнение системы, такими образом, для определения параметра решётки достаточно наблюдения двух узлов. Обозначим координаты наблюдаемых узлов ( z 11 , z ₁₂ ) и ( z ₂₁, z ₂₂ ) , соединённых ребром решётки, тогда можно получить выражение, устанавливающее связь между углом вращения ф , длиной стороны a и координатами узлов на проекции:

a = z ii z 22    ^{( Z} 12 + z 21 )

cos ф ( z 11 + z ₂₂)

.

Таким образом, для определения стороны кубической решётки в случае её наблюдаемости достаточно измерить координаты двух соседних узлов на плоскости и угол поворота решётки относительно оси вращения.

• 4.    Анализ достаточных условий наблюдаемости тетраэдра

Рассмотрим достаточные условия наблюдаемости для конфигурации узлов ячейки, образующей правильный тетраэдр. Из тетраэдров можно образовать как моноклинные, так и гексагональные кристаллические решётки.

Рассмотрим задачу определения наблюдаемости тетраэдра, вращающегося вокруг произвольной оси, проходящей через одну из его вершин. Таким образом, наблюдению на проекции доступны три вершины тетраэдра, поскольку четвёртая вершина будет совпадать с началом координат O (рис. 7).

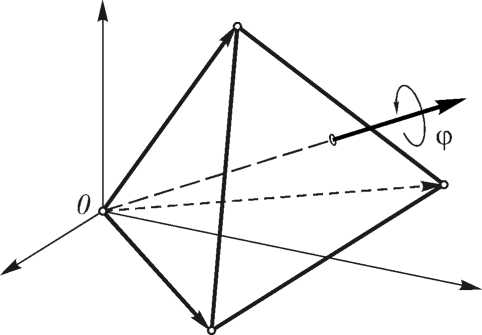
Рис. 7. Схема вращения тетраэдра

Определим начальное положение тетраэдра следующим образом: одно из рёбер совпадает с осью X ₁ , прилегающая к этому ребру грань лежит в плоскости X ₁ OX ₂ , тогда координаты вершин правильного тетраэдра с длиной ребра L определяются как:

(Хц, xX2, Xn) = ( L ,0,0), c1 (Vs +1) + c2 (Vs -1) = 0 и

Ф          2V2

tan =------TF--\----"F-

• ² ( c 1 — c 2 ) ( V3 — 1 ) + 2 V2 c s

  приведены на рис. 8.

  
  

Таблица 2. Выражения, определяющие ненаблюдаемость вершин правильного тетраэдра

Рис. 8. Схемы проекций узлов правильного тетраэдра, при которых тетраэдр является ненаблюдаемым

В случаях, когда узлы являются наблюдаемыми, используя (9), можно записать систему уравнений второй степени для оценивания параметров наблюдения X _k и длины ребра L . Обозначим координаты наблюдаемых узлов ( z 11 , z ₁₂ ) и ( z ₂₁, z ₂₂ ) , тогда

⁽ x 21 , x 22 , x 23 )

( x ₃₁ , x ₃₂ , x ₃₃ ) =

f L LV3 J

2^0 I,

V ²²   )

L , -L, Ц²

V 2 2Vs Vs

можно получить выражение, устанавливающее связь между углом вращения ф , длиной ребра L и коор-

динатами узлов на проекции:

Запишем условие (20), учитывая обозначения (13), (4) при наблюдении каждой из вершин правильного тетраэдра (22), в виде таблицы соответствий 2.

Наблюдаемость узлов невозможна в случаях:

Уз ^z _n ^— 2 z 22 ^— z 21 23cos ф

±

±

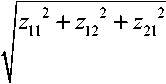
⁺ z 22 ^{— z} 11 ^z 12 ^— z 21 z 22

^/3 ⁽ z 11 z 22 ⁺ z 12 z 21 )

23cos ф

ф

• 1)    sin "2 = 0, т.е. Ф = 2 n k , k e Z - соответствует

полному обороту тетраэдра.

• 2)    ( c 1 )( c 1 + c ₂ V3)( c 1 4b + c ₂ + 2 c 3 V2) = 0 ,

Таким образом, для определения длины ребра правильного тетраэдра достаточно измерить координаты двух вершин на плоскости проекции и угол поворота тетраэдра относительно оси вращения, знак плюс или минус в выражении (23) выбирается так, чтобы длина ребра была положительной величиной.

Заключение

На основе теории описания кинематики вращательного движения с использованием дифференциальных кинематических уравнений были получены необходимые и достаточные условия наблюдаемости проекций кристаллических решёток.

Рассмотрены частные случаи для кубической ячейки и правильного тетраэдра. Получены выражения для определения геометрических параметров кристаллических решёток.

Предметом дальнейшего исследования является получение в явном виде достаточных условий наблюдаемости узлов решётки не только для вращательного, но и для поступательного движения решётки , приводящее к использованию сложных операторов проецирования, учитывающих 2 и более слоёв решётки. Необходимо также рассмотреть подходы к решению задачи определения наблюдаемости параметров решётки и их оценивания в общем случае, для большего числа проекций.

Работа выполнялась при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 02.740.11.0841), гранта РФФИ 12-01-00237-а, гранта Президента РФ поддержки ведущей научной школы НШ-4128.2012.9, программы фундаментальных исследований РАН-ОНИТ6 в рамках выполнения государственного задания № 8.3195.2011 Минобрнауки РФ.