О некоторых актуальных проблемах современной астродинамики: взгляд инженера-практика

За более чем 50-летнюю историю космонавтики были разработаны разнообразные вычислительные методы для задач астродинамики, которые способствовали решению обширного многообразия практических проблем. Вместе с тем развитие космонавтики выдвигает новые и новые задачи. С другой стороны, появление в прикладной математике последнего десятилетия ряда новых методов позволяет по-новому взглянуть на некоторые уже решённые задачи астродинамики и/или расширить их постановку. К числу подобных методов можно отнести алгоритмы для задач линейного программирования высокой размерности, которые были разработаны на основе работ Л.Т. Хачияна [1] и Н. Кар-маркара [2] и послужили основой разработки эффективных алгоритмов внутренней точки [3]. Их название связано с тем, что в отличие от симплекс-метода, перебирающего угловые точки многогранника допустимых решений, вычислительный процесс в этих алгоритмах происходит внутри допустимого множества решений. Эти алгоритмы имеют полиномиальную сходимость и, что очень важно для практических задач, защищены от вырожденности. Они позволяют решать задачи с десятками и сотнями тысяч неизвестных переменных. Другим примером новых направлений прикладной математики являются методы вычислительной геометрии [4], которые позволяют оперировать с геометрическими областями и вычислять их пересечения, обьединения и т. п.

Статья представляет изложение доклада автора на «XXXIII Академических чтениях по космонавтике» (г. Москва, 26–30 января 2009) и содержит краткий обзор проблем и методов современной астродинамики, которые, по мнению автора, представят практический интерес в ближайшем будущем.

• II.    Оптимизация траекторий выведения перспективных пилотируемых космических кораблей

Разработка в России пилотируемого космического корабля (КК) нового поколения (взамен летающего более 40 лет КК

«Союз») подразумевает, в том числе создание более безопасных и комфортных условий полета космонавтов. Наиболее критичным и напряжённым этапом пилотируемого полета является выведение КК ракетой-носителем (РН) на орбиту. Важнейшим элементом здесь выступает система аварийного спасения экипажа (САС), которая используется в случае аварии РН и должна обеспечивать отделение КК с последующим управляемым движением по возможности с приведением в заданные районы в окрестности трассы выведения (рис. 1). Одним из определяющих факторов выбора траекторий САС является необходимость ограничения максимальных перегрузок для различных начальных условий. Эти требования существенно влияют на выбор траектории РН вплоть до уменьшения выводимой на орбиту массы КК. В качестве иллюстрации можно указать, что использование пологой траектории выведения с высотами перигея и апогея орбиты h _n x h _a = 135 x 440 км приводит к уменьшению максимальной перегрузки для траекторий САС с 20 до 12 единиц, по сравнению с траекторией выведения на круговую орбиту h _n = h _a ~ 200 км (при выводимой массе m выв ~ 14 т).

Рис. 1. Траектория выведения с учётом САС

Таким образом, в отличие от классической постановки по оптимизации траектории РН с учётом традиционных ограничений по перегрузке и скоростному напору, необходимо принимать во внимание также ограничения для очень широкого спектра возможных траекторий движения САС. В целом решение этой проблемы приводит к весьма сложным задачам оптимизации траекторий.

III.    Управление орбитальными группировками космических аппаратов III.1.    Координированный полет — Formation Flying

В последние десятилетия бурное развитие получили проекты орбитальных группировок космических аппаратов (КА), выполняющих единую целевую задачу. К их числу можно отнести спутниковые системы (CC) связи (ИРИДИУМ, ГЛОБАЛ-СТАР и др.), группировки КА для дистанционного зондирования Земли, астрофизических наблюдений, радиоинтерферометрии с большой базой, совместный полет группировки КА в окрестности одной рабочей точки геостационарной орбиты и т. п.

В части управления орбитальным движением КА необходимо выполнение определённых требований по поддержанию орбитальной структуры группировки в долговременном масштабе (месяцы, годы). В группировках КА с координированным управлением внешние силы воздействуют на орбитальное движение всех КА, как правило, практически одинаково, и их относительные различия очень малы. Поэтому для управления может применяться не только традиционная коррекция движения с использованием двигательной установки, но и формируемые целевым образом отличия сил различной природы: атмосферного торможения; электромагнитных сил; давления солнечного света и т. п.

• III.2.    Методический пример — управление спутниковой системой

Долговременное управление (СС) из N спутников заключается в поддержании близкой к исходной её орбитальной структуры. Рассматривается низкоорбитальная однородная СС на круговых орбитах (орбиты всех спутников имеют одинаковые наклонения и высоты), подверженная атмосферному торможению [5]. Предписанные относительные положения спутников в системе можно представить в виде ориентированного графа (рис. 2). Спутники в этом графе являются вершинами. Ребро от одного до другого спутника представляет дугу, описывающую взаимное положение смежных спутников вдоль орбиты, по отклонениям которой от номинального значения необходимо осуществлять управление. Один из спутников назначается головным и является корнем этого ориентированного графа (такой подход называют «движущийся за лидером» — «Leader Following»). Этот граф является деревом. Каждое дерево с N вершинами имеет N — 1 рёбер, то есть управляемых дуг — предписанных конфигурацией системы относительных смещений спутников вдоль орбиты. Для двух смежных в графе спутников из различных орбитальных плоскостей это требуемый фазовый сдвиг между спутниками этих плоскостей. Смещения спутников относительно друг друга δnj определяются по отношению к этим предписанным значениям (j — номер ребра в графе, j — 1, ..., N — 1). Каждому графу может быть сопоставлена матрица инцидентности размерности N х (N — 1). Имеются различные варианты построения таких графов. Два противоположных варианта — дерево с минимальной длиной и одинаковой длиной всех путей, равной 1 (рис. 3а), и цепной граф (рис. 3б) с максимальной длиной, равной N — 1. Их матрицы инцидентности представлены ниже (показаны только ненулевые элементы):

Г1 — 1 1

ских членов) от предписанных номинальных положений и отклонения орбитальных периодов спутников от опорной орбиты: x ^T — ( 5n T , A T ^T ) — ( 5n ₁ , 5n ₂ , ..., 5n N - 1 , A T i , A T ₂ , ..., A T n ), где Sn — А n — A щ +1 , а A n i — смещения вдоль орбиты от единого опорного движения для всех спутников СС. Имеется линейное соотношение между смещениями A n ^T — (A n ₁ , A n ₂ , ..., A n N ) и относительными отклонениями 5n — A t A n .

—

At —

At —

.

.

.

—

—

.

.

.

—

.

—

.

—1

—1

—1 1 — 1

Управление относительными положениями вдоль орбиты с использованием трансверсальных маневров основано на осред-нённых уравнениях, описывающих вековое движение в окрестности опорной круговой орбиты. Вектором фазовых координат являются смещения положений спутников вдоль орбиты (без учёта периодиче-

Спутниковая система

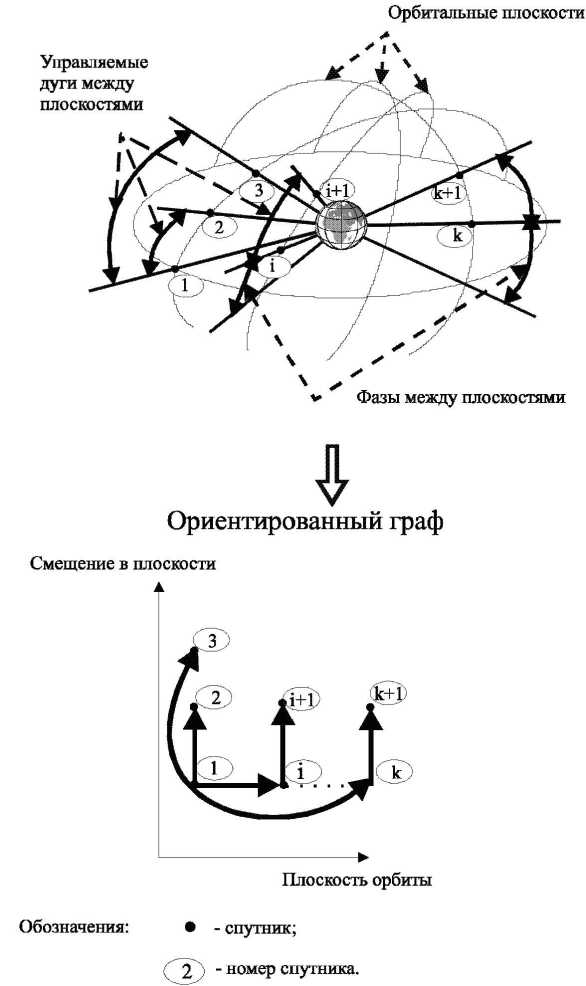
Рис. 2. Представление СС в виде графов

Переходная матрица может быть записана в виде

A—

I N - 1     A t

O (N - 1) xN   I N

где I N - ₁ , I N — единичные матрицы и O ( N - ₁) _xN — нулевая матрица. Долговременное поведение СС при постоянном периоде между корректирующими маневрами может быть описано дискретным ли-

нейным матричным уравнением в стандартной форме:

x (k + 1) = Ax (k) + Bv (k),      (1)

где BT = [0(N-1)xN IN] матрица управления размерностью (2N — 1) x N, vT = (△ Vl,△ V2, ..., △VN) вектор управления — вектор характеристических скоростей корректирующих маневров, k —но- мер шага коррекции.

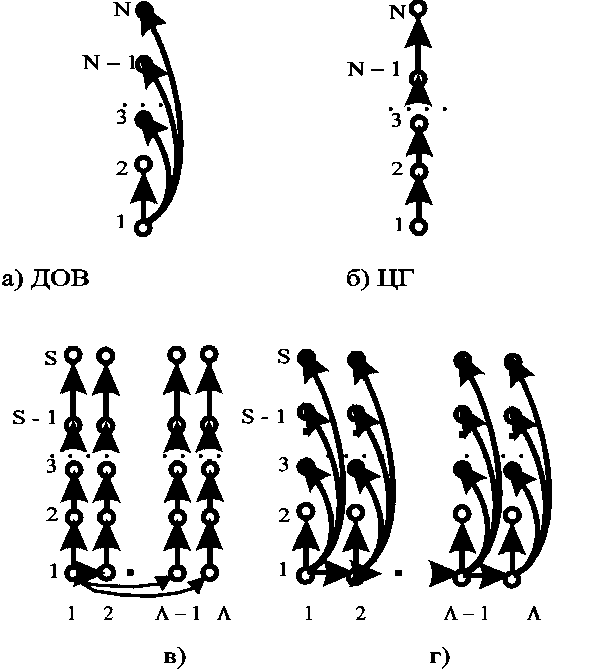
Рис. 3. Примеры графов

Система (1) полностью управляема, поскольку ранг матрицы управляемости ра- вен 2N — 1. Задача управления СС, подверженной постоянно действующим возмущениям, в большей степени является задачей регулирования, а не терминального управления [5]. Для задач регулирования предпочтительным является использование линейно-квадратического критерия:

1 k=k f

J = — ^ ^ (xT (k + 1) Gxx(k + 1)+ k=0

+vT (k) Gv v (k)), где Gx — неотрицательно-определённая, а Gv — положительно определённая весовые квадратные матрицы с размерностями соответственно 2N — 1 и N. Весовые матрицы Gx и Gv определяют соответственно относительное соотношение вклада ошибок вектора состояния x и вектора управления v в функционал. В такой постановке оптимальным является линейный закон управления с обратной связью, обеспечивающий устойчивость замкнутой системы

v (k) = —F (k) x (k), где F (k) — матрица коэффициентов обратной связи, определяемая из решения матричного уравнения Риккати. Детальное описание линейно-квадратического управления СС с использованием графов, пример решений и моделирования для СС из 12 спутников приведены в [5].

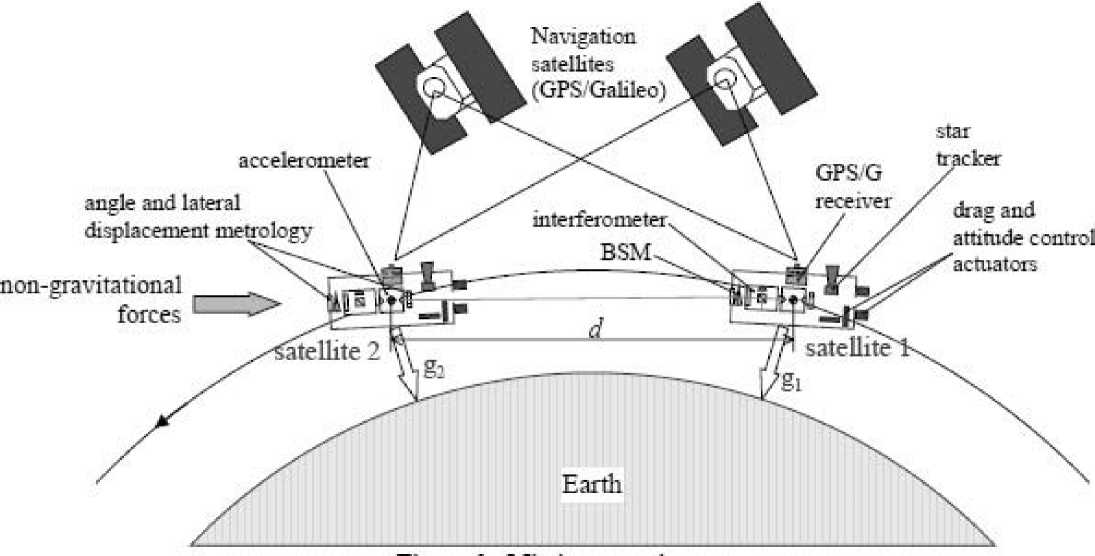
Рис. 4. Проект GOCE

• III.3.    Примеры практических проектов

  В 2014 году НАСА планируется реализация проекта MMS по исследованию магнитосферы Земли, где орбитальная группировка будет включать 4 КА, которые должны образовывать тетраэдр в области, близкой к апогею высокой эллиптической орбиты (рис. 4) [6].

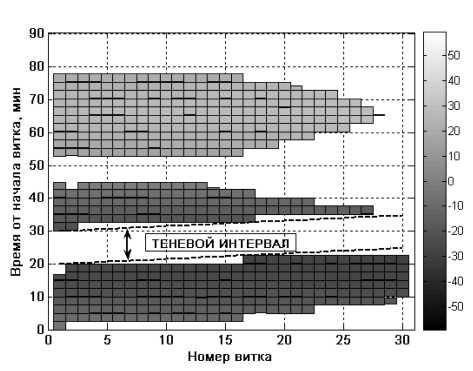
Рис. 5. Пример распределения маневров сближения с малой тягой

Разработан европейский проект GOCE (Gravity Field and Steady — State Ocean Circulation Explorer) по долговременным измерениям гравитационного поля Земли и моделирования с исключительно высокой точностью и пространственным разрешением формы Земли [7]. Будут использоваться два КА, движущиеся на заданном расстоянии друг от друга на одних и тех же круговых орбитах высотой 325 км (рис. 5).

Обширный обзор работ и проектов по координированному управлению (по состоянию на 2004 год) представлен в [8].

IV.    Сближение и инспекция на орбите

• IV.1. Сближениe на околокруговых орбитах c малой тягой

Традиционно при сближении и стыковке КА на орбите используются двигатели большой (или средней) тяги. Практический интерес представляют также КА, осуществляющие сближение и/или инспекцию с малой тягой. Оптимизация таких траекторий кардинально отличается от траекторий с большой тягой, где выполняется, как правило, несколько маневров, которые хорошо аппроксимируются импульсным представлением. При наличии малой тяги маневры становятся продолжительными, в том числе сплошными многовит-ковыми, что существенно осложняет задачу. При оптимизации траектории зачастую необходимо учитывать ряд ограничений. Например, для КА с электрореактив-ными двигателями, как правило, ограничивается суммарная продолжительность работы на витке и вводятся запреты на работу двигателей в тени Земли.

Для решения подобных задач можно использовать методы множеств псевдоимпульсов [9–12]. Краткое резюме этих методов представлено в приложении. Решение различных задач сближения с малой тягой при наличии ограничений представлено в [10]. В качестве примера на рис. 5 показано распределение маневров сближения на 30-витковом интервале при наличии ограничений [10]. Каждый из маневров включает несколько сегментов — закрашенные прямоугольники (справа от графиков показана шкала, определяющая интенсивность их закраски в соответствии с изменением курсового угла вектора тяги).

• IV.2. Автоматический КА «Orbital Express»

Одним из самых интересных и перспективных проектов последнего времени в США является система «Orbital Express» (OE) для сближения и/или инспекции некооперируемых объектов на орбите [13]. Она разрабатывается под эгидой военного агентства по перспективным разработкам (DARPA) ВВС США фирмой «Боинг» и НАСА. Первый полет OE начался 8 марта 2007 года, и 5 мая было осуществлено сближение и захват спутника. При эксперименте использовалось два космических аппарата — ASTRO (Autonomous Space Transport Robotic Operations) и NextSat (Next generation serviceable Satellite). Последний выступал в качестве экспериментальной цели. Ряд операций OE были полностью автоматическими и по возможности автономными — сближение, операции облета, причаливание, захват пассивного космического аппарата и перелеты устройства орбитальной замены (Orbital Replacement Unit). Пример траектории относительного движения в одном из полетных тестов показан на рис. 6. Отметим, что все операции выполнялись автоматически.

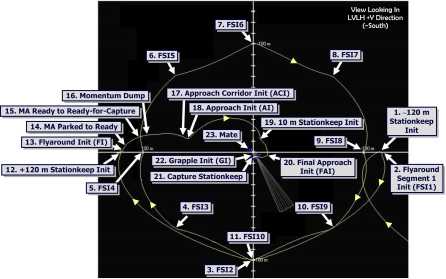
Рис. 6. Пример траектории относительного движения «Orbital Express»

V. Проектирование спутниковых систем для сложных видов обзора

Большинство традиционных методов проектирования спутниковых систем ассоциируются с простейшим зональным или глобальным, непрерывным или периодическим обзором, связанным с видимостью изолированных точек на поверхности Земли. Предлагается новый геометрический подход для более сложного вида непрерывного обзора, связанного с географическими областями [14]. Возможен полный или частичный обзор географических областей. Это означает, что в любой момент времени область полностью или частично находится в мгновенном поле обзора одного из спутников системы (рис. 7). Ключевой идеей методов является использование единого двумерного пространства для представления движения спутниковой системы и требований по обзору. Размерности этого пространства — инерциальная долгота восходящего узла (или прямое восхождение восходящего узла) и время. Требования по обзору любой географической области могут быть отображены в этом пространстве полигоном точек, а спутниковая система представляется как равномерно движущаяся решётка (рис. 8). В любое время, как минимум, одна вершина решётки должна находиться внутри поли- гона. Оптимальная конфигурация спутниковой системы соответствует максимально разряженной решётке. Решетка должна также удовлетворять целочисленным ограничениям для числа орбитальных плоскостей и числа спутников в плоскости.

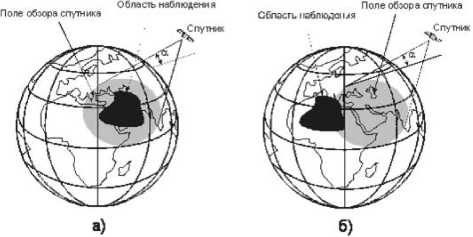
Рис. 7. Виды обзоров географических областей

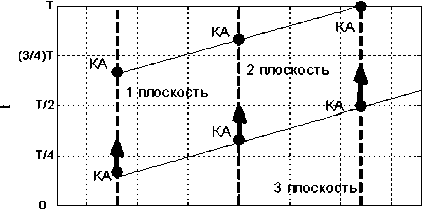
150   -100    -50      0      50     100    150

Q. град

Рис. 8. Представление СС в двумерном пространстве

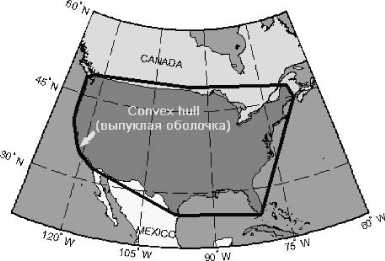
Рис. 9. Географическая область обзора

В качестве примера непрерывного обзора географической области рассматривается непрерывный обзор континентальной части территории США (рис. 9). Это означает, что в любой момент времени имеется, по крайней мере, один спутник в СС с мгновенным полем обзора, включающим всю область. Или, другими словами, в любое время, как минимум, один спутник виден со всех точек территории США. Для этого случая функция обзора может быть рассчитана на основе выпуклой оболочки для граничных точек. На рис. 10 показаны двумерные отображения условий видимости некоторого набора граничных точек этой области для КА на круговой орбите с высотой h = 10 300 км и наклонением i = 45°. С использованием алгоритмов вычислительной геометрии построена соответствующая область пересечения и опре-

ТРУДЫ МФТИ. — 2009. — Том 1, № 3 делён максимальный параллелограмм. Оптимальное решение соответствует СС из 15 спутников.

Этот метод подходит для проектирования СС непрерывного обзора на круговых и эллиптических орбитах [15, 16], а также для СС периодического обзора. В последнем случае принадлежность вершины полигону должна выполняться с некоторым временем перерыва.

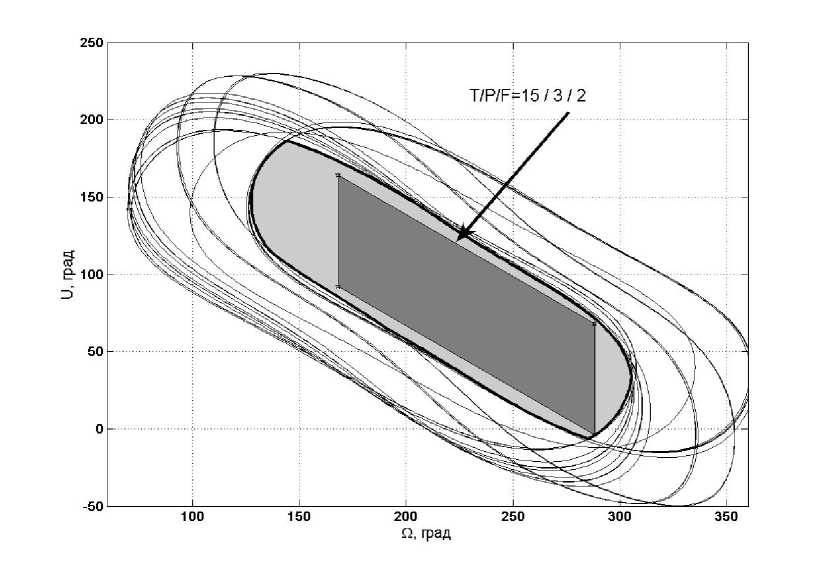
Рис. 10. Отображение условий видимости граничных точек и решение для СС

VI. Спутниковые системы на высокоэллиптических орбитах VI.1. Выбор элементов орбит с учётом возмущений

Часто используемые на практике высокоэллиптические орбиты типа «Молнии» с критическим наклонением имеют очень сложную эволюцию. При построении СС из КА на таких орбитах необходимо учитывать особенности, вызванные существенным влиянием лунно-солнечных гравитационных возмущений и тессераль-ных гармоник гравитационного поля Земли. Уровни возмущений для различных

КА определяются соответственно положением их орбит в инерциальном пространстве и прохождением трасс относительно Земли. Это затрудняет выделение общей части возмущений для всех КА системы в отличие от возмущений, связанных с зональной частью разложения модели гравитационного поля Земли. Проблема может быть частично решена путём искусственного введения отклонений орбитальных элементов относительно некоторых номинальных значений в пределах, обеспечивающих выполнение целевых условий и реализующих существенное снижение затрат на поддержание орбит КА (за счёт использования естественной эволюции орбит) [17]. Прицельные отклонения выбираются для каждого КА системы с учётом планируемой эпохи начала полета и его длительности.

• VI. 2. Оптимальное маневрирование по поддержанию высокоэллиптической орбиты

Долговременное поддержание высокоэллиптических орбит заключается в сохранении отклонений орбитальных элементов и/или трассы КА в заданных пределах относительно их номинальных значений путём периодического проведения корректирующих маневров. В зависимости от требований к КА корректируемыми могут быть не все орбитальные элементы, а какие-то комбинации. Простейшим случаем является коррекция поддержания трассы КА. Если КА входит в спутниковую систему и необходимо согласование движений смежных спутников, то может возникнуть необходимость коррекции времени прохождения. Отличительной особенностью поддержания является движение КА в окрестности номинальной орбиты и использование малых корректирующих импульсов и/или маневров с малой тягой (например, путём применения электрореактивных двигателей).

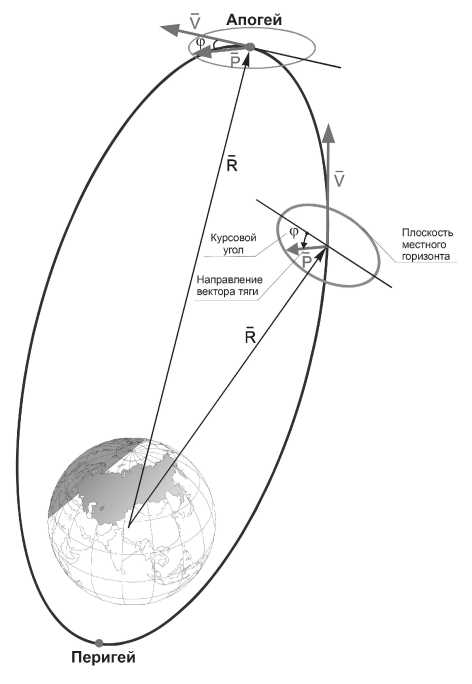
Рис. 11. Ориентация вектора тяги

Рассматривается долговременное управление орбитой КА с периодом ∼ 24

часа, критическим наклонением i = 63 , 4 ° , аргументом перигея ш _п = — 90 ° и эксцентриситетом e = 0 , 27 [9]. Предполагается, что вектор управления — вектор тяги — может быть ориентирован в плоскости местного горизонта произвольным образом (рис. 11). Целью управления является сохранение трассы полета КА относительно Земли (долгота восходящего узла ± 1 ° ) и близких к номинальным значениям орбитальных элементов i , ω _π и e .

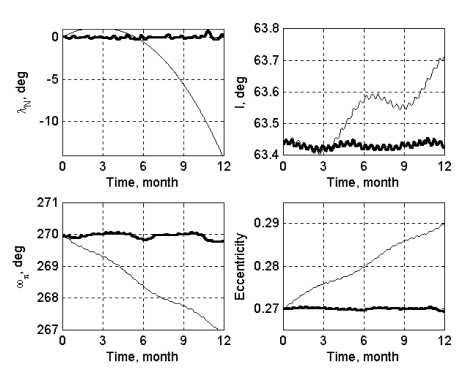
Рис. 12. Изменение орбитальных элементов на годовом интервале

Для решения используется уже упоминавшийся метод на основе множеств псевдоимпульсов [9–12, Приложение]. Поскольку орбита является эллиптической, то для дискретизации по времени предпочтительней использовать неодинаковые по времени сегменты — меньшие в окрестности перицентра и большие в окрестности апоцентра. Каждый виток разделяется на одинаковые по изменению на сегменте значения истинной аномалии, а соответствующие границам сегментов времена рассчитываются по параметрам номинальной орбиты на основе уравнения Кеплера. При расчёте отклонений для невозмущённой траектории учитывались нецентральность гравитационного поля Земли, гравитационные возмущения от Луны и Солнца и давление солнечного света. Результаты моделирования на годовом интервале представлены на рис. 12, где представлено изменение долготы восходящего узла λ, наклонения орбиты i, аргумента перигея ωπ и эксцентриситета ε. Для каждого параметра показано их поведение при наличии коррекций орбиты (сплошные толстые линии) и при пассивном полете (тонкие ли- нии). Пример распределения маневров по виткам для одного из месячных периодов изображен на рис. 13 в виде закрашенных прямоугольников высотой, эквивалентной их длительности. Интенсивность фона закраски соответствует значению курсового угла по вертикальной шкале, находящейся справа.

Характеристическая скорость за месяц AVx=7.79 м/с

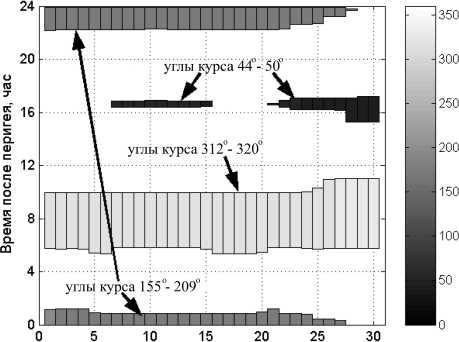
Номер витка

Рис. 13. Пример распределения маневров на месячном интервале

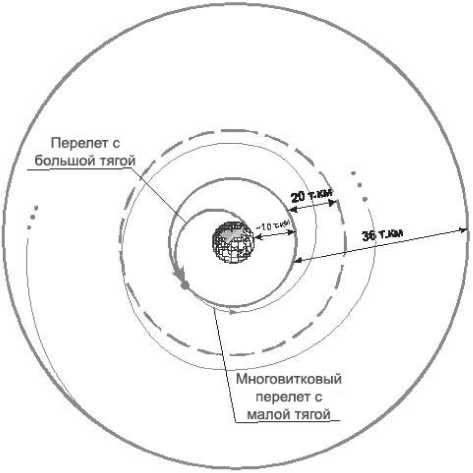
Рис. 14. Комбинированное выведение на геостационарную орбиту

VII.    Выведение с малой тягой на геостационарную орбиту

В настоящее время интенсивно прорабатываются проекты увеличения выводимой массы на самую востребованную в коммерческом плане геостационарную орбиту. Большинство из них связано с ис- пользованием электрореактивных двигателей с малой тягой, что предопределяет формирование спиральных многомесячных траекторий выведения с низких околоземных орбит. С практической точки зрения такие оптимальные траектории могут быть нежелательными для бортовой аппаратуры КА, поскольку предполагают длительный полет в радиационных поясах Ван Аллена. Поэтому в ряде случаев более предпочтительными могут быть комбинированные схемы выведения (рис. 14), в которых осуществляется «быстрый» перелет с использованием двигателей большой тяги, по крайней мере, через первый пояс Ван Аллена (или через оба пояса) на промежуточную орбиту и далее длительный перелет на геостационарную орбиту с малой тягой. Проектирование и оптимизация таких схем полета представляет большой практический интерес.

VIII.    Проблемы дальнего космоса

В последние десятилетия выполнен большой цикл работ по низкоэнергетическим межпланетным траекториям перелетов (по-английски их часто называют «Superhighway») [18]. Существующие, например, в системах «Земля–Луна» и «Земля–Марс» точки либрации могут быть связаны друг с другом длительными траекториями перелетов, требующими малые по меркам межпланетных перелетов затраты топлива. На базе подобных траекторий может быть построена экономичная транспортная система обеспечения будущих межпланетных экспедиций.

В рамках создания инфраструктуры лунных экспедиций и её долговременного освоения практический интерес могут представлять так называемые квазицик-лические траектории полета КА в системе «Земля–Луна». Речь идёт о долгопериодических траекториях, включающих периодический облет Луны и Земли [19] (рис. 15). Для поддержания подобных орбит требуются очень малые затраты характеристической скорости порядка ∼ 10–100 м/с в год. Они могут использоваться для транспортных операций обеспечения связи и т. д. Возможные типы таких траекторий рассматриваются в рамках плоской задачи трёх тел. Отметим, что подобные квазициклические траектории существуют в системе «Земля–Марс» и также могут найти применение в марсианских программах. В последние годы в США (JPL) этому направлению уделяют большое внимание. Для лунных экспедиций большой интерес представляет использование орбитальной станции или некоторой базы, размещенной в точке либрации L1 [20].

чевую идею метода поясним простейшим случаем с ориентацией вектора тяги КА в некоторой плоскости. На любом сегменте i вектор тяги может быть ориентирован в этой плоскости произвольным образом и время работы двигателя не долж-

но превышать длительности этого сегмен та Ati max, а приобретаемый на этом сег-

менте импульс скорости будет не более

^A V i max

a max

A t i max ,

где a _max

макси-

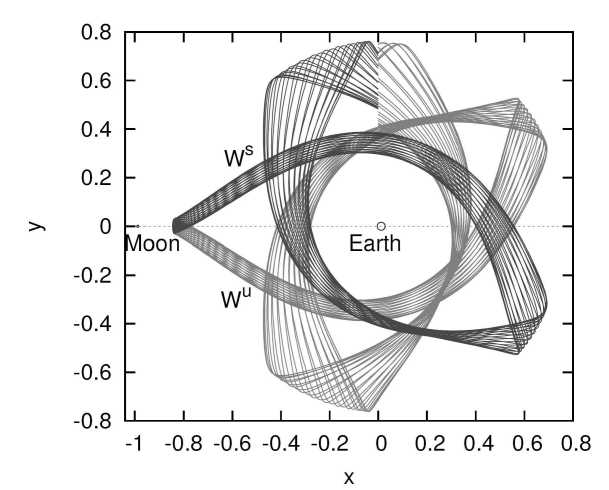
Рис. 15. Квазициклические траектории между Землей и Луной

мальное ускорение от работы ДУ. Возмож-

ные направления вектора тяги представим в виде дискретного набора ориентаций (рис. 16а). Предположим, что на сегменте возможно выполнение k псевдоимпульсов, однако их сумма по модулю не должна превышать A V i max . Если нас интересует оптимальное (в смысле затрат характеристической скорости) решение, то в нём не может быть более двух смежных псевдоимпульсов, поскольку сумму двух или трёх, или более несмежных векторов псевдоимпульсов всегда можно заменить двумя смеж-

IX.    Заключение

В изложенном обзоре кратко описаны ряд перспективных задач современной астродинамики, представляющих практический интерес. Некоторые из них отражены в упрощённом постановочном плане, а по ряду проблем показаны возможные направления решения.

X.    Приложение. Методы на основе множеств псевдоимпульсов

Основу метода составляет дискретизация траектории для интервала времени перелета [0 ,t f ] на n малых, в общем случае неодинаковых, сегментов A t i = t i +1 — t i и введение для каждого из них множества псевдоимпульсов, определяющих возможные направления вектора тяги. Использование ограничений для сумм псевдоимпульсов каждого сегмента позволяет привести задачу к форме классического линейного программирования с ограничениями в виде равенств и неравенств. Клю-

ными псевдоимпульсами, имеющими меньшую сумму. Пусть A V _iopt — оптимальное решение для i -го сегмента (рис. 16б). Из элементарных геометрических соображений очевидно, что наилучшим приближением к оптимальному решению из имеющегося набора псевдоимпульсов с дискретными ориентациями в общем случае будет решение для двух смежных псевдоимпульсов, между которыми располагается оптимальный импульс A V _iopt . В общем случае для пространственной ориентации вектора тяги множество псевдоимпульсов можно представить в виде близкого к равномерному распределения точек на сфере или какой-то её части [9, 10].

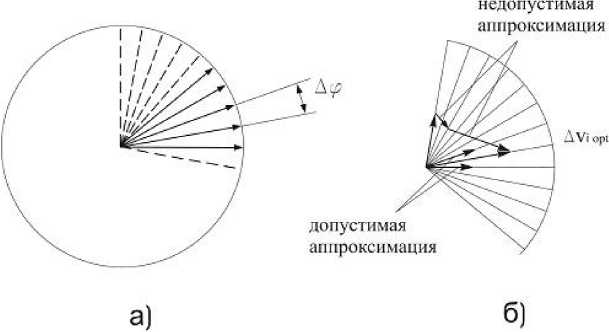
Рис. 16. Множество псевдоимпульсов в плоскости

Введём вектор неизвестных переменных X , включающий все псевдоимпульсы

на всех сегментах, размерностью ( n х к ):

X T = [Д V '1⁰) , Д V , ⁽²⁾ , ..., Д V^k ⁾ ,

Д V , ⁽¹⁾ , Д V > ⁽²⁾ , ..., Д V (k ⁾ , ..., Д V (k ⁾ ] .    (2)

Тогда для этого вектора можно записать линейное неравенство:

AX С b, (3)

где A — матрица размерностью n х ( n х к ), имеющая следующую структуру (показаны только ненулевые элементы):

Вектор b ^T = [11 ... 11] имеет размерность, равную числу сегментов.

Краевые условия в виде некоторой функции F ( Y,a,t ) размерностью s от некоторых параметров траектории КА (описываемых вектором Y ) и вектора реактивного ускорения a представим в виде линейного матричного уравнения

Д P f = P f - P f = A e X,      (4)

где P f = F ( Y,a,t f ) — вектор краевых условий, Pf — значение краевых условий на невозмущённой (то есть пассивной) траектории, A e — матрица размерностью s х ( n х к ):

" dFi    dFi         dFi    dFi         dFi"

dv ( j )    di l ²     ...    dv 2 j )    dV ₂⁽²⁾    ’"dv

Ae =     ,

∂Fs    ∂Fs         ∂Fs    ∂Fs

• . dv(j)   dV^2)   ...   dV2(j)   dV2(2)   ’"   dV^k).

где dF l /dV i ⁽ j ) — частные производные.

Определим вектор коэффициентов qT = [11 ... 1 1] из (n х к) элементов для равномерных сегментов. В случае неравномерных по времени сегментов этот вектор представим в виде q [Д t 1 max, ..., Д tn max]. Элементы этого вектора также могут служить весовыми коэффициентами в приоритетности использования различных режимов тяги, времён проведения маневров и т. п.

В итоге проблема оптимизации траектории формулируется как задача классического линейного программирования: найти вектор X (2), минимизирующий линейный функционал

J = min ( q^T • X)

при линейных ограничениях в виде матричного неравенства (3), равенства (4) и неотрицательных значениях всех элементов вектора X : 0 С Д V i ⁽ j ) С Д V i _max .

В изложенной формулировке задача имеет весьма высокую размерность, однако для подобных задач имеются эффективные алгоритмы внутренней точки [1–3].

Методы на основе множеств псевдоимпульсов позволяют достаточно гибко учитывать требования, связанные с особенностями двигательных установок КА, ориентацией вектора тяги, операционными ограничениями на выполнение маневров и дополнительными краевыми условиями во внутренних точках траектории. Число маневров на траектории не ограничивается и не фиксируется, а определяется автоматически в результате обработки решения задачи линейного программирования. Методы могут использоваться также для проектного анализа и оценок влияния различных ограничений на характеристики КА, их детальное описание с соответствующими примерами приведено в [9–12].